Statistiques à deux variables
Introduction
Dans certaines étude statistiques, on peut supposer un lien entre deux caractères d'une population. Pour étudier ces éventuelles liaisons, on va s'intéresser simultanément à deux caractères $x$ et $y$ d'une même population.
On définit ainsi une série statistique à deux variables $x$ et $y$ prenant des valeurs $x_1 , \dots , x_i , \dots , x_n$ et $y_1 , \dots , y_i , \dots , y_n$.
Le mur d'une habitation est constitué par une paroi en béton et une couche de polystyrène d'épaisseur variable $x$ (en cm). On a mesuré, pour une même épaisseur de béton, la résistance thermique $y$ de ce mur en $m^2$ °C par watt pour différentes valeurs de $x$. On a obtenu les résultats suivants :

Pour des véhicules légers (Puissance administrative de 9 à 11 chevaux), on a relevé les consommations moyennes (en L/100 km) et les vitesses correspondantes (en km/h) suivantes :

Nuage de points
Chaque couple $(x_i ; y_i)$, peut être représenté dans un repère orthogonal par un point $M_i$. L'ensemble de ces points constitue le nuage de point représentant la série statistique.
Réalisation d'un nuage de point :
- Enregistrer les données dans deux listes X et Y.
- la commande Xcas est :
scatterplot(X,Y,affichage=bleu+point_width_3)
Représenter les deux nuages de points des exemples précédents.
Point moyen
On appelle point moyen d'un nuage de $n$ points $M_i$ de coordonnées $(x_i ; y_i)$ le point $G$ de coordonnées : $$x_G=\bar{x}=\frac1n \sum_{i=1}^n x_i \qquad \textrm{et} \qquad y_G=\bar{y}=\frac1n \sum_{i=1}^n y_i .$$
Déterminer les coordonnées des points moyens des exemples précédents
Ajustement affine : méthode des moindres carrés
On ne présente pas en détail la méthode, mais il faut retenir qu'une droite de régression par cette méthode minimise la somme des carrés des distances entre les points et la droite.
Obtenir l'équation de la droite de régression linéaire :
- Enregistrer les données dans deux listes X et Y.
- Taper :
linear_regression(X,Y)
La droite ainsi trouvée est la droite de régression de X en Y.
Représenter le nuage de points et l'équation de la droite de régression :
- Enregistrer les données dans deux listes X et Y.
- la commande Xcas est
scatterplot(X,Y,affichage=bleu+point_width_3),linear_regression_plot(X,Y,affichage=rouge+line_width_3)
Coefficient de corrélation linéaire
Le coefficient de corrélation linéaire d'une série statistique double de variables $x$ et $y$ est le nombre $r$ défini par : $$r=\frac{\sigma_{xy}}{\sigma_x \times \sigma_y} .$$
- Le nombre $r$ vérifie : $-1 \leq r \leq 1$.
- Il existe une "bonne" corrélation entre $x$ et $y$ (et donc on peut admettre un ajustement affine) lorsque $|r|$ est suffisamment voisin de $1$.
Obtenir le coefficient de corrélation linéaire :
- Enregistrer les données dans deux listes X et Y.
- Taper :
covariance(X,Y)/(stddev(X)*stddev(Y))
Déterminer les coefficient de corrélation linéaire des deux séries initiales
Exercices
Le tableau suivant donne la moyenne y des maxima de tension artérielle en fonction de l'âge x d'une population donnée.

- Représenter graphiquement le nuage de points M(x; y)
- Calculer, à $10^{-2}$ près, le coefficient de corrélation linéaire entre x et y. Le commenter.
- Déterminer une équation de la droite de régression de y en x et la représenter. (Les coefficients seront arrondis à 0,001 près.)
- Une personne de 70 ans a une tension de 16,1. Quelle serait sa tension théorique en utilisant la droite de régression ? Comparer avec la tension réelle.
Toutes les valeurs numériques demandées seront arrondies à $10^{-3}$. L'étude, durant les cinq dernières années, du nombre de passagers transportés annuellement sur une ligne aérienne a conduit au tableau suivant :

- Calculer le coefficient de corrélation linéaire de la série (x; p). Commenter ce dernier.
- On pose $yi = ln pi$ où $ln$ désigne la fonction logarithme népérien.\\ Il suffit sous xcas d'écrire
y:=ln(p) - Représenter le nuage de points $Mi(x_i; y_i)$ dans un repère orthogonal du plan. Peut-on envisager un ajustement affine de ce nuage ? Justifier par un calcul.
- Déterminer par la méthode des moindres carrées une équation de la droite de régression D de y en x.
- Déduire de la question précédente une expression de p en fonction de x.
- En admettant que l'évolution constatée se poursuive les années suivantes, utiliser la relation obtenue à la question précédente pour estimer le nombre de passagers transportés au cours de l'année de rang 7.
Article intéressant pour se poser des questions
Vous pouvez vous rendre sur cet article afin de vous poser quelques questions avec ce générateur aléatoire de comparaisons absurdes.
Accès à l'articleDu côté des calculatrices
Calculatrice numworks disponible : le site numworks
Le tableau suivant donne l'évolution des bénéfices d'une société : 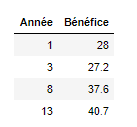
La vidéo suivante vous permet de traiter l'exercice avec la calculatrice :
Faire des statistiques à deux variables en langage python
Le tableau suivant donne l'évolution des bénéfices d'une société : 
Le code proposé dans l'espace Trinket ci dessous permet d'obtenir :
- Le nuage de points avec la droite de régression
- Le point moyen
- L'équation de la droite de régression
Observer les éléments de ce code. Vous pouvez faire quelques modifications pour comprendre ce code.
Des explications en vidéo :

Compléter le code ci-dessous, en comparant avec l'exercice précédent.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International