Les équations différentielles.
Une équation différentielle est un nouveau type d’équation où l’inconnue est une fonction.
De nombreux phénomènes continus sont décris par une fonction f plusieurs fois dérivables sur un intervalle I et définie comme solution d’une équation différentielle où interviennent une ou plusieurs de ses dérivées.
- Quelques exemples :
- Effet d’un amortisseur de voiture
- Etablissement d’un courant électrique à travers un circuit RLC
- La décharge d’un condensateur
- L’élimination d’un médicament dans le sang
- Le fléchissement d’une tige
Pour rappel, la dérivée première correspond à la vitesse instantanée et la dérivée seconde correspond à l'accélération instantanée.
En xcas la commande pour trouver les solutions d'une équation différentielle est "desolve ...."

Pour chercher les solutions de l'équation $ y'+4y=0 $ avec comme conditions initiales $ y(0)=3 $

En utilisant xcas, retrouver les solutions des équations différentielles proposées

Le premier ordre
Les solutions sont du type $f(x)=k e^{-ax} +\frac{b}{a}$ où $k$ est une constante réelle quelconque. $k$ dépend des conditions initiales.
Une vidéo d'un cas simple :
La méthode de recherche des solutions dans le cas général : méthode
En utilisant xcas, retrouver les solutions des équations différentielles proposées.
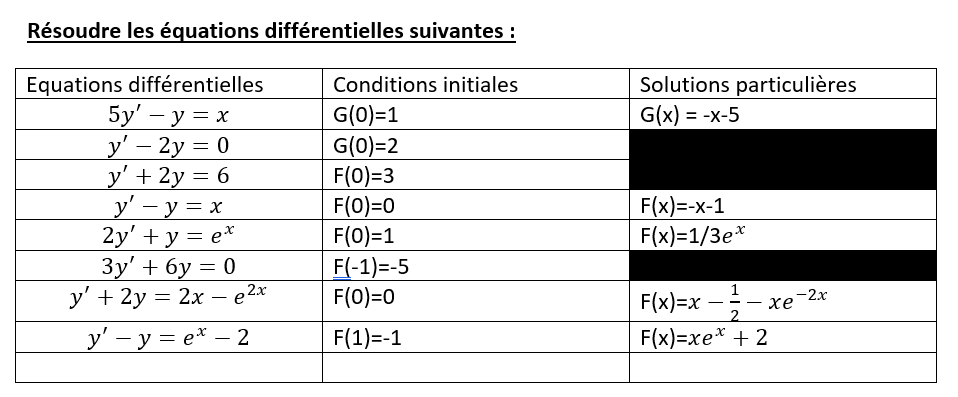
Problèmes
En utilisant xcas, résoudre le problème suivant :
