Demander le programme !



Un problème initial
La ville de Königsberg était une ville de Prusse puis une des principales villes de l'Empire Allemand avant d'être céder à l'URSS en 1945. Cette ville est désormais appelée Kaliningrad et fait partie de la Fédération de Russie.
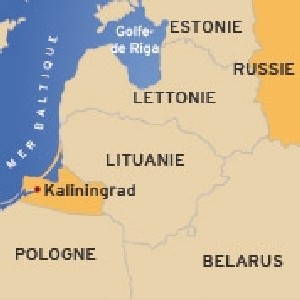
Cette ville s'étendait au $XVIII^e$ siècle autour de deux îles situées sur le fleuve Pregel. Ces deux îles étaient reliées entre elles par un pont. Six autres ponts reliaient les rives de la rivière à l'une ou l'autre des deux îles, comme représenté sur le plan ci-dessous.
La légende raconte que certains habitants de cette ville cherchaient lors de promenade à passer une fois et une seule par chacun des ponts pour revenir au point de départ (évidemment, ils ne pouvaient traverser l'eau du Pregel que'en passant par un des ponts.)
Est-ce possible ? Si oui, par quel chemin ?
Les habitants ont cherché des solutions et l'un d'eux, le grand mathématicien Euler, a réussi en 1735 à répondre à la question précédente. Pour cela, il a développé des outils mathématiques à la base de la théorie des gaphes, théorie qui sera effleurée dans ce cours.
Modélisation :
Une des idées d'Euler fut de modéliser la situation pour réduire à l'essentiel le problème ; il a représentée la configuration précédente des ponts dans la ville en la figure ci-dessous :
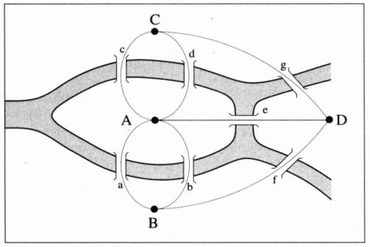
figure qui peut être déformée ainsi :
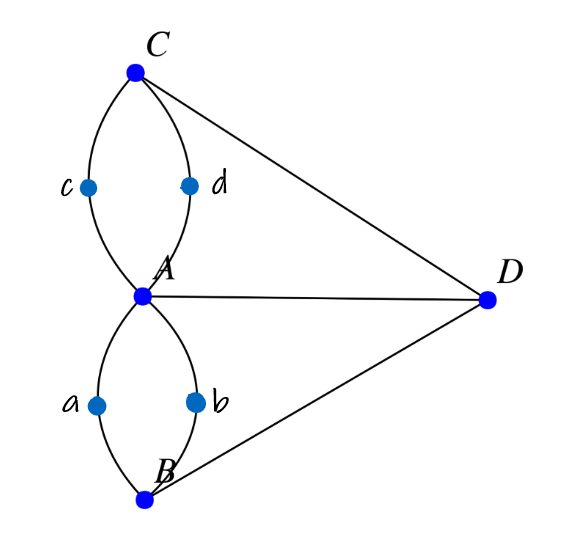
Cet objet synthétique s'appelle un graphe où les points A, B, C et D sont des sommets et les traits reliant ce points des arêtes.
Graphe non-orienté
Vocabulaire sur les graphes non-orientés
-
Un graphe non-orienté est un ensemble formé de sommets reliés par des arêtes.
-
Deux sommets reliés par une arête sont dits adjacents.
-
Un graphe est dit complet lorsque tous ses sommets sont adjacents.

-
Les sommets $A$ et $B$ sont adjacents car ils sont reliés par une arête : l'arc $\displaystyle \overset{\frown}{AB} $.
-
Les sommets $B$ et $C$ ne sont pas adjacents car on ne peut pas passer directement d'un point à l'autre grâce à un seul arc.
-
Le graphe de l'exemple n'est donc pas un graphe complet.
-
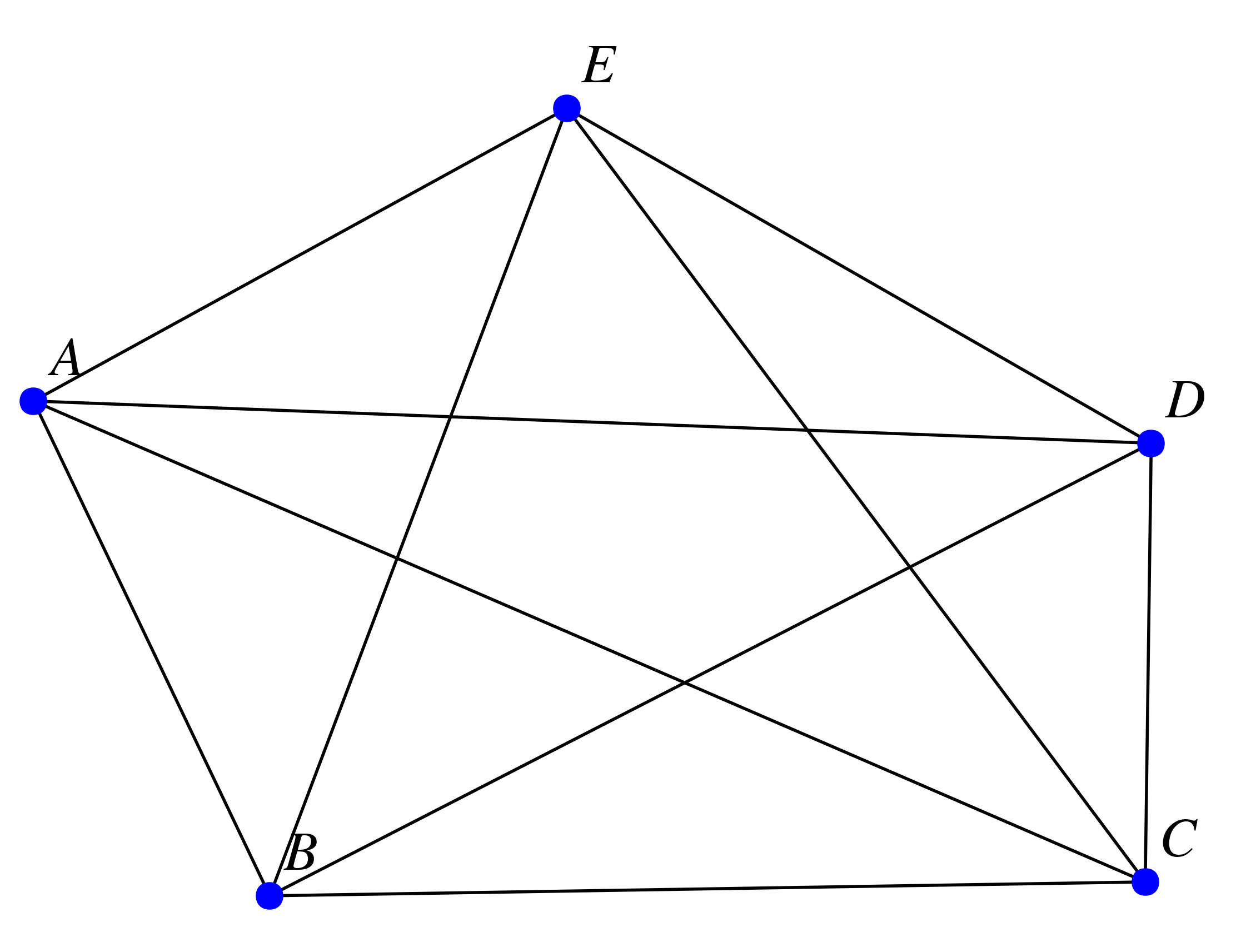
Le graphe ci-dessous est par contre complet :
-
L'ordre d'un graphe est le nombre de sommets de ce graphe.
-
Le degré d'un sommet est le nombre d'arêtes dont ce sommet est une extrémité.

-
Ce graphe est d'ordre 4.
-
Le sommet $A$ est de degré 5.
-
Les sommets $B$, $C$ et $D$ sont de degré 3.
-
La somme des degrés des sommets d'un graphe non-orienté est égale au double de son nombre d'arêtes.
-
Le nombre de sommets de degré impair d'un graphe non-orienté est pair.
-
Justifier la première affirmation de la proporiété précédente.
-
Démontrer, à l'aide d'un raisonnement par l'absurde, la seconde affirmation de la propriété précédente.
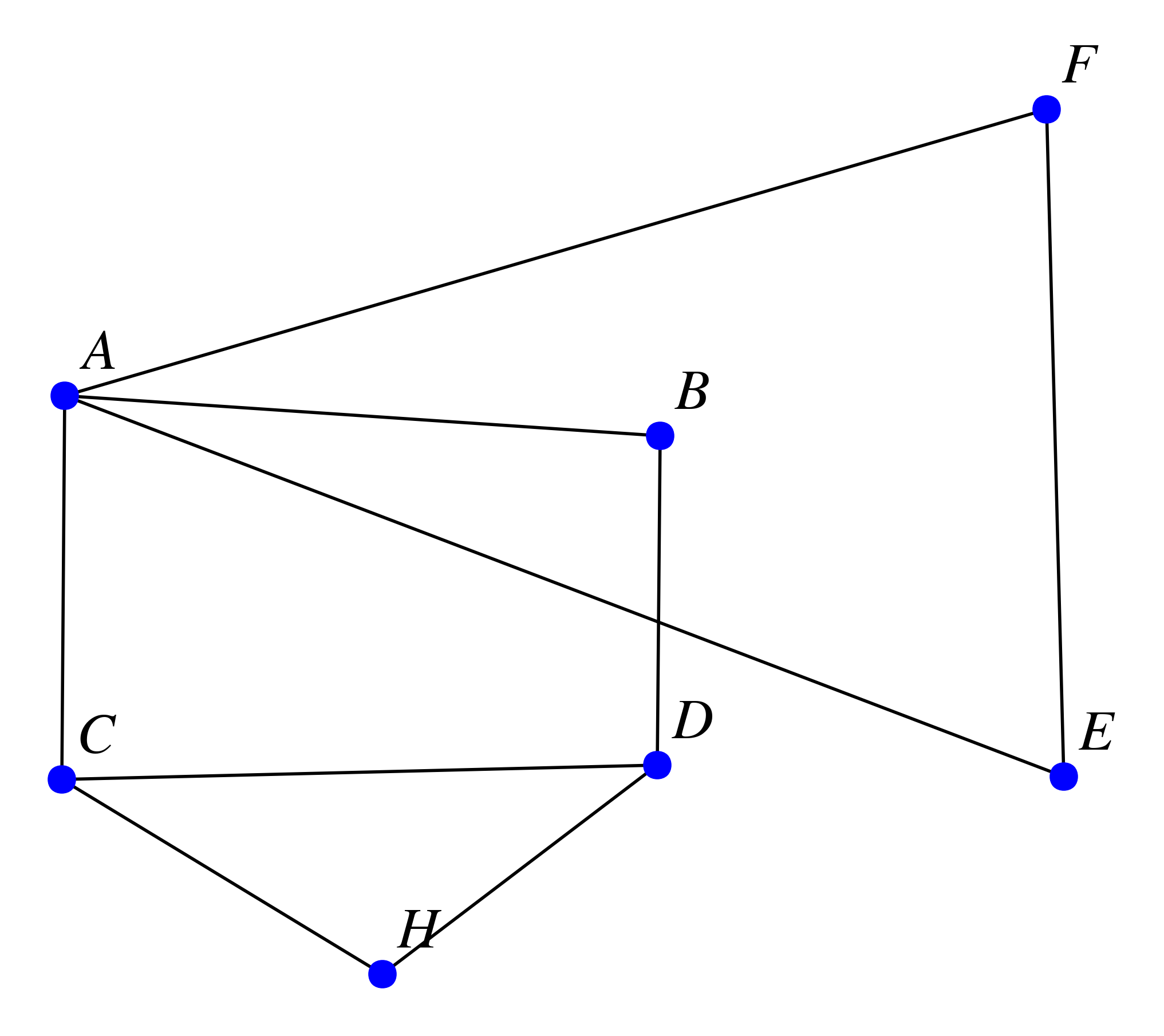
On considère le graphe représenté ci-dessous ; il modélise le plan d'un village. Les arêtes du graphe représentent ses rues et les sommets les croisements de celle-ci.
-
Quel est l'ordre du graphe ?
-
Déterminer le degré de chacun des sommets.
-
En déduire le nombre de rues de ce village.
-
Quel est le nombre de sommets de degré impair ?
-
Citer deux sommets adjacents.
-
Ce graphe est-il complet ?
Parcours sur un graphe non-orienté
-
Dans un graphe non-orienté, on appelle chaîne une suite d'arêtes consécutives reliant deux sommets adjacents (éventuellement confondus).
-
La longueur d'une chaîne est le nombre d'arêtes qui composent la chaîne.
-
Une chaîne fermée est une chaîne dont l'origine de la première arête et l'extrémité de la dernière arête sont confondues.
-
Un cycle est une chaîne fermée dont les arêtes sont distinctes.
-
Un graphe est dit connexe si deux sommets distincts quelconque peuvent être reliés par une chaîne.
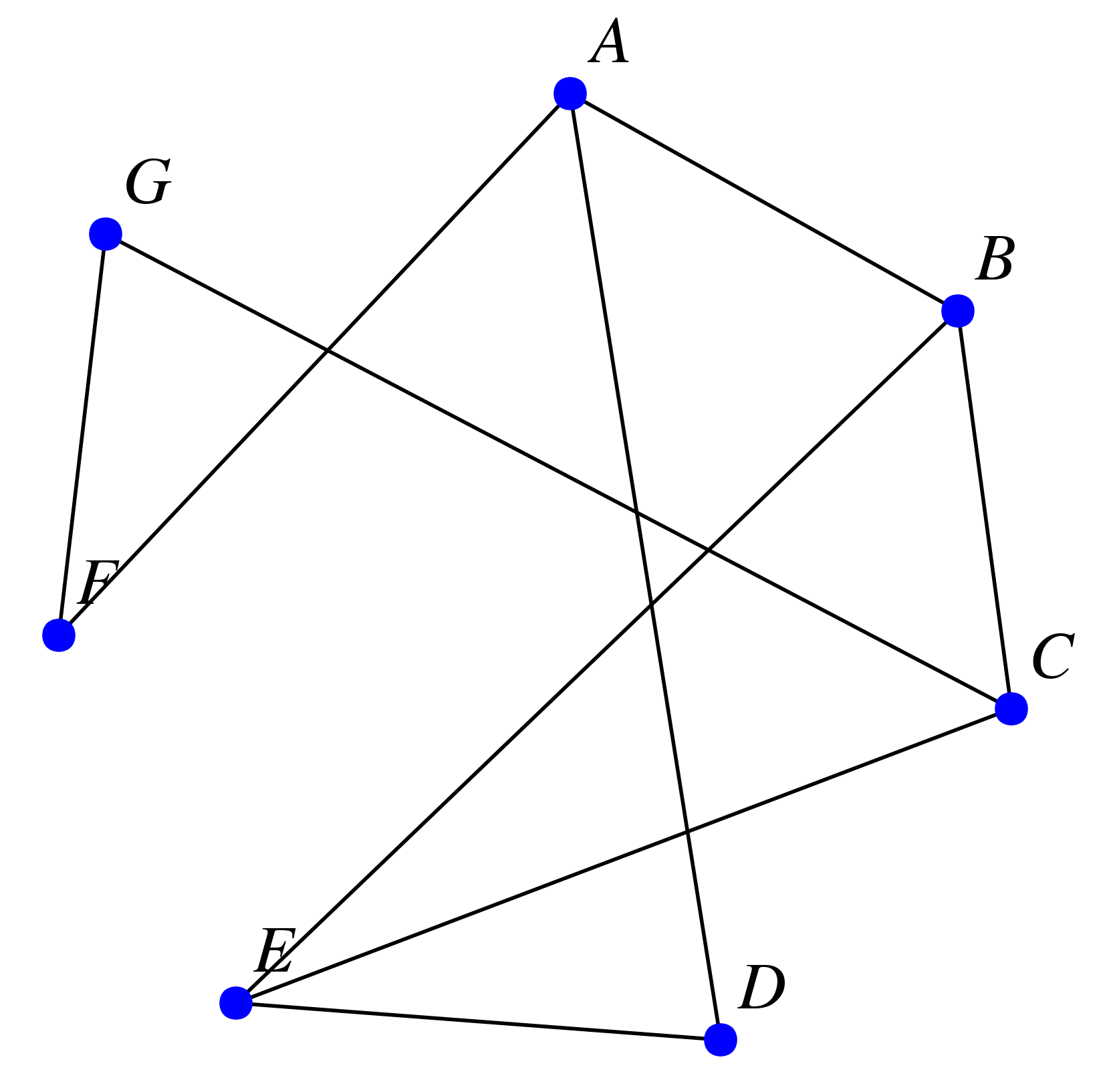
On considère le graphe non-orienté suivant :
-
Quel est l'ordre du graphe ?
-
Quel nom peut porter la chaîne $B - C - E - B$ ? Quelle est sa longueur ?
-
Déterminer une chaîne de longueur 8 reliant $F$ à $D$
-
Déterminer un cycle d'origine $G$.
-
Le graphe est-il connexe ?
Graphe orienté
Vocabulaire
-
Un graphe orienté est un graphe dont les arêtes sont orientées : chaque arête ne peut être parcourue que dans le sens de la flèche.
-
Ces arêtes orientées sont aussi appelés arc.
-
Dans un graphe orienté, on appelle chemin de longueur $n$ une succession de $n$ arcs tels que l'extrémité de chacun est l'origine du suivant (sauf pour le dernier arc).
-
On dit que le chemin est fermé lorsque l'origne du premier arc coïncide avec l'extrémité du dernier.
-
Un chemin fermé composé d'arcs tous distincts est appelé circuit.
Proxémie des termes suivant l'orientation ou non du graphe :
| Graphe non-orienté | Graphe orienté |
|---|---|
| arête | arc |
| chaîne | chemin |
| cycle | circuit |
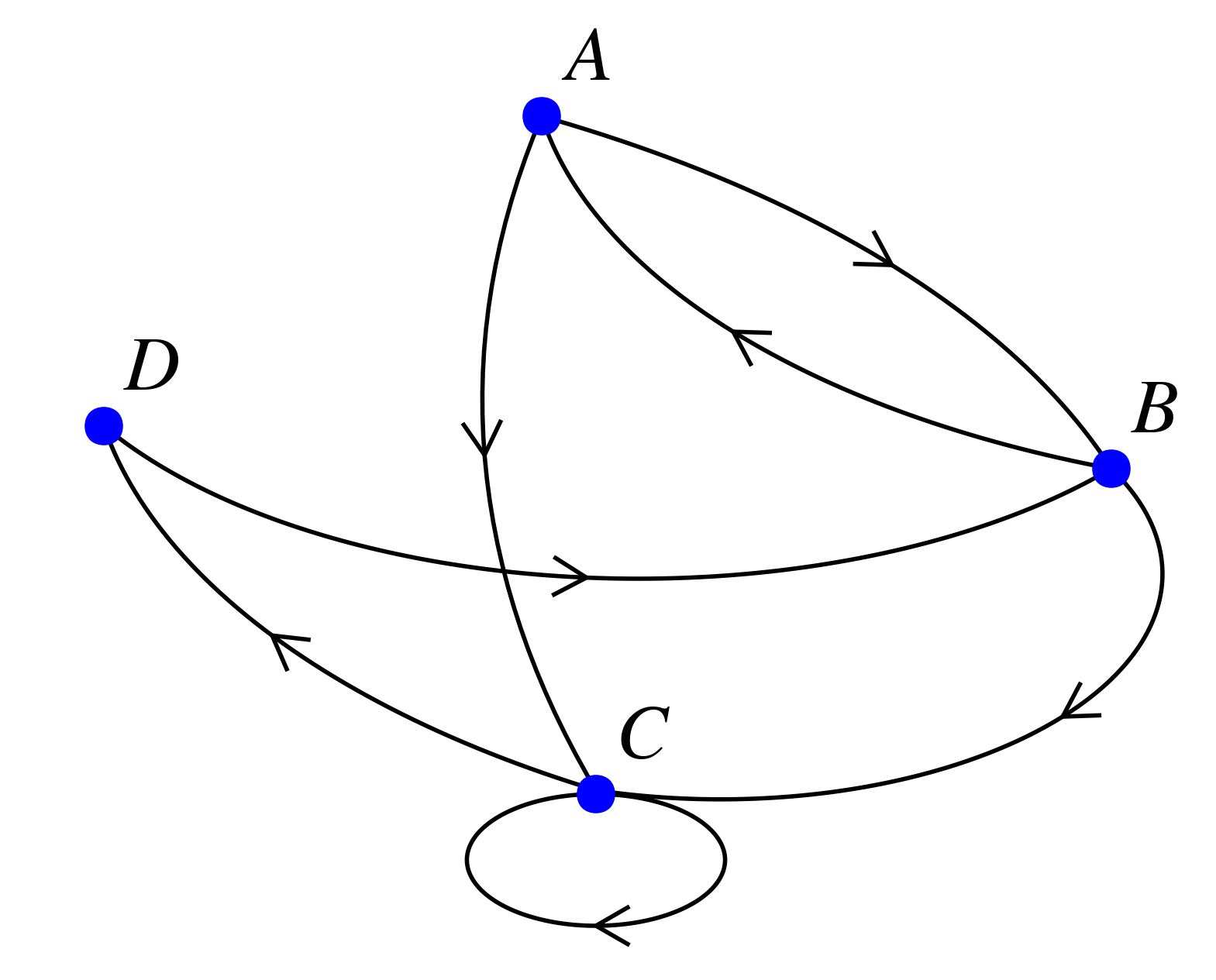
Voici un graphe :
-
On peut se rendre du sommet $B$ vers le sommet $C$ mais pas du sommet $C$ vers le sommet $B$ : c'est donc un graphe orienté.
-
On peut se rendre du sommet $B$ vers le sommet $A$ et du sommet $A$ vers le sommet $B$ : deux arcs sont nécessaires.
-
À partir du sommet $C$, on peut se rendre au sommet $C$ grâce à un circuit.
-
Le chemin $ B - A - C - C - D - B - A$ est un chemin de longueur 6.
-
Le chemin $A - C - D - B - A$ est un circuit de ce graphe.
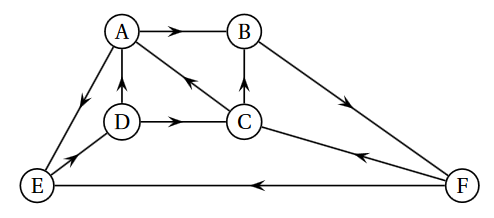
Le graphe suivant représente le plan d’une ville. Les arcs du graphe représentent ses avenues commerçantes, en prenant en compte le sens de circulation, et les sommets du graphe les carrefours de ces avenues.
-
Est-ce un graphe orienté ou non-orienté ? Pourquoi ?
-
Quel est l'ordre du graphe ?
-
Proposer un chemin de longueur 4 d'origine $F$ et d'extrémité $B$.
-
Proposer un circuit passant par tous les sommets.
Matrice d'adjacence d'un graphe
Un journaliste britannique d’une revue consacrée à l’automobile doit tester les autoroutes françaises. Pour remplir sa mission, il décide de louer une voiture et de circuler entre six grandes villes françaises : Bordeaux ($B$),Lyon ($L$), Marseille ($M$), Nantes ($N$), Paris ($P$) et Toulouse($T$). Le réseau autoroutier reliant ces six villes est modélisé par le graphe ci-dessous sur lequel les sommets représentent les villes et les arêtes les liaisons autoroutières entre ces villes.
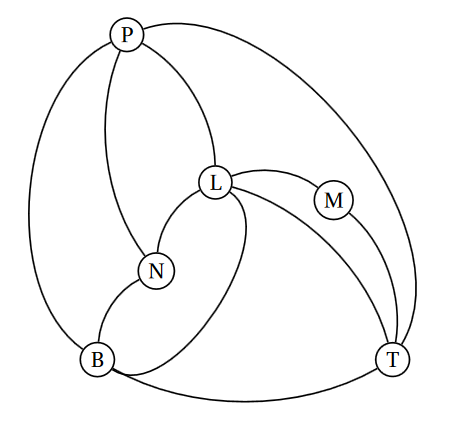
Plutôt que de représenter la situation par un graphe, le journaliste visualise le réseau avec un tableau dans lequel il met 1 s'il existe une liaison directe entre les deux villes correspondant à la case et 0 sinon. Il obtient donc le tableau ci-dessous :
| Villes | $B$ | $L$ | $M$ | $N$ | $P$ | $T$ |
|---|---|---|---|---|---|---|
| $B$ | 0 | 1 | 0 | 1 | 1 | 1 |
| $L$ | 1 | 0 | 1 | 1 | 1 | 1 |
| $M$ | 0 | 1 | 0 | 0 | 0 | 1 |
| $N$ | 1 | 1 | 0 | 0 | 1 | 0 |
| $P$ | 1 | 1 | 0 | 1 | 0 | 1 |
| $T$ | 1 | 1 | 1 | 0 | 1 | 0 |
Par exemple, il existe une autoraute reliant directement Paris $P$ à Nantes $N$, donc il y a le nombre 1 dans les cases repérées par $N$ et $P$ ;
il n'existe pas d'autoraute reliant directement Marseille $M$ à Bordeaux $B$, donc il y a le nombre 0 dans les cases repérées par $M$ et $B$.
Pour synthétiser l'information (en mémorisant le fait que les villes sont rangées dans l'ordre alphabétique), il suffit de considérer le tableau extrait contenant les données chiffrées. On peut appeler ce tableau matrice. Voici la matrice représentant la situation :
$$G = \begin{pmatrix} 0 &1 &0 &1 &1 &1 \\ 1 &0 &1 &1 &1 &1\\ 0 &1 &0 &0 &0 &1\\ 1 &1 &0 &0 &1 &0 \\ 1 &1 &0 &1 &0 &1\\ 1 &1 &1 &0 &1 &0 \end{pmatrix} $$La matrice associée à un graphe d'ordre $n$ est la matrice carrée de taille $n$, où le terme de la $i$-ème ligne et de la $j$-ème colonne est égal au nombre d'arêtes (ou d'arc) partant du sommet $i$ pour arriver au sommet $j$.
Cette matrice s'appelle la matrice d'adjacence de ce graphe.
Le graphe ci-dessous représente, dans un aéroport donné, toutes les voies empruntées par les avions au roulage. Ces voies, sur lesquelles circulent les avions avant ou après atterrissage, sont appelées taxiways. Les sommets du graphe sont les intersections. Les arcs du graphe représentent les voies de circulation (les « taxiways ») en prenant en compte le sens de circulation pour les avions dans les différentes voies ainsi que le temps de parcours pour chacune en minute(s).
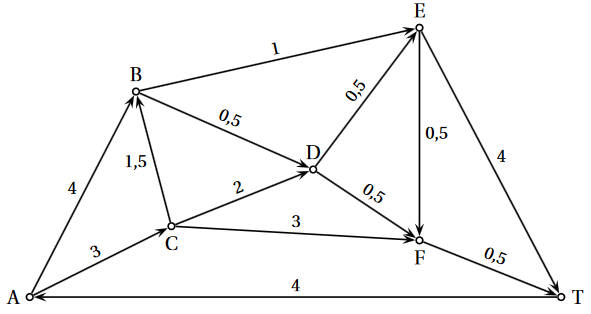
En rangeant les sommets dans l'ordre alphabétique, la matrice $M$ d'ajacence de ce graphe est
$$M = \begin{pmatrix} 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{pmatrix}$$En effet peu importe les distances écrites et, par exemple, :
-
Il y une liaison directe de $A$ vers $B$, donc le deuxième coefficient ($2^{ème}$ car l'arrivée $B$ est le deuxième sommet) de la première ligne (celle du départ $A$) vaut 1.
-
Il n'y a pas de liaison directe de $C$ vers $A$, donc le premier coefficient (colonne correspond à l'arrivée $A$) de la troisième ligne (celle du départ $C$) est 0.
Le graphe suivant représente le plan d’une ville. Les arcs du graphe représentent ses avenues commerçantes, en prenant en compte le sens de circulation, et les sommets du graphe les carrefours de ces avenues.

-
Écrire la matrice $M$ associée à ce graphe. (On rangera les sommets dans l’ordre alphabétique).
-
Cette matrice est-elle symétrique ? Pourquoi ceci était-il prévisible ?
Exercices
Graphe non-orienté
On a schématisé ci-dessous une partie du plan du métro londonien par un graphe $\Gamma$ dont les sommets sont les stations et les arêtes sont les lignes desservant ces stations.
Chaque station de métro est désignée par son initiale comme indiqué dans la légende.
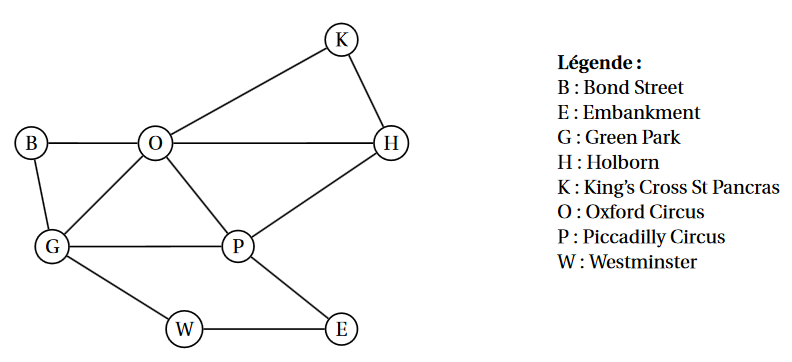
-
Proposer un cycle qui permettrait de passer par chacune des stations de métro du graphe $\Gamma$.
-
Déterminer en justifiant si le graphe $\Gamma$ est connexe.
-
Déterminer en justifiant si le graphe $\Gamma$ est complet.
-
Donner la matrice d'adjacence $M$ du graphe $\Gamma$ (les sommets seront rangés dans l'ordre alphabétique).
-
On appelle chaîne eulérienne une chaîne qui permet de passer par toutes les arêtes une et une seule fois.
Existe-t-il une chaîne eulérienne à ce graphe $\Gamma$ ? Si oui, en donner une.
Sarah, une jeune étudiante en géologie, souhaite partir en voyage en Islande avec des amis. Elle a loué
une voiture tout terrain pour pouvoir visiter les lieux remarquables qu'elle a sélectionnés.
Sarah
a construit le graphe ci-dessous
dont les sommets représentent les lieux à visiter et les arêtes représentent les routes ou pistes :
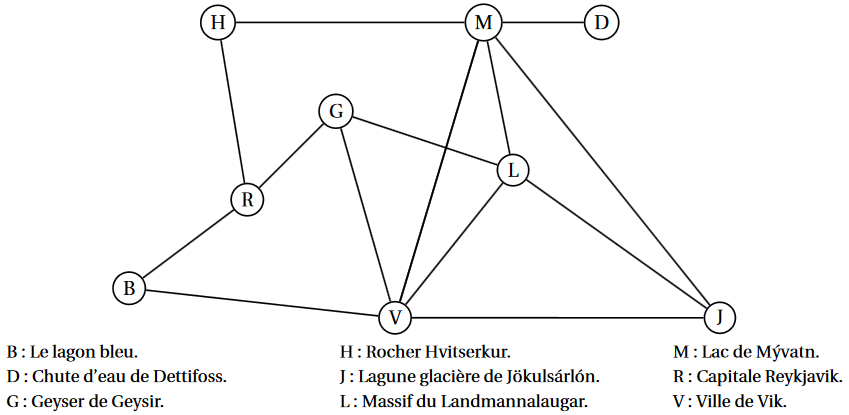
-
Dans cette question, chaque réponse sera justifiée.
-
Déterminer l'ordre du graphe.
-
Déterminer si le graphe est connexe.
-
Déterminer si le graphe est complet.
-
-
-
Dresser un tableau dans lequel apparaîtront chaque arête avec son degré.
-
Comment peut-on en déduire le nombre d'arêtes du graphe ?
-
-
On appelle $M$ la matrice associée au graphe précédent sachant que les sommets sont placés dans l'ordre alphabétique.
$$M = \begin{pmatrix} 0 &0 &0 &0 &0 &0 &0 &1 &1 \\ 0 &0 &0 &0 &0 &0 &1 &0 &0 \\ 0 &0 &0 &0 &0 &1 &0 &1 &1 \\ 0 &0 &0 &0 &0 &0 &1 &1 &0 \\ 0 &0 &0 &0 &0 &1 &1 &0 &1\\ 0 &0 &1 &0 &1 &0 &1 &0 &1\\ \ldots&\ldots&\ldots&1 &1 &1 &0 &0 &1\\ \ldots&\ldots&\ldots&1 &0 &0 &0 &0 &0\\ \ldots&\ldots&\ldots&0 &1 &1 &1 &0 &0 \end{pmatrix}$$Il manque certains coefficients de la matrice $M$. Compléter et recopier uniquement la partie manquante de cette matrice.
Graphe orienté
Un parcours sportif est composé d'un banc pour abdominaux, de haies et d'anneaux. Le graphe orienté ci-dessous indique les différents parcours conseillés partant de D et terminant à F.
Les sommets sont: D (départ), B (banc pour abdominaux), H (haies), A (anneaux) et F (fin du parcours).
Les arcs représentent les différents sentiers reliant les sommets.
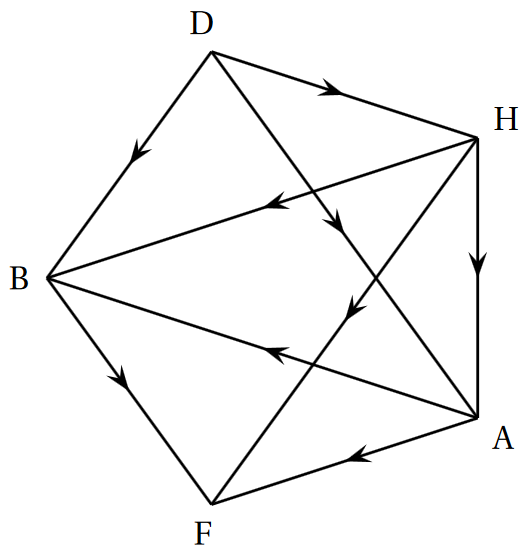
-
Quel est l'ordre du graphe?
-
Est-il possible de suivre un parcours en passant par toutes les étapes ?
-
On note $M$ la matrice d'adjacence de ce graphe où les sommets sont rangés dans l'ordre alphabétique. Déterminer cette matrice $M$.
-
Le responsable souhaite ajouter une barre de traction notée T. De nouveaux sentiers sont construits et de nouveaux parcours sont possibles.
La matrice d'adjacence $N$ associée au graphe représentant les nouveaux parcours, dans lequel les sommets sont classés en ordre alphabétique, est :
$$N = \begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ \end{pmatrix}$$Compléter le graphe précédent en ajoutant les arcs nécessaires pour que le graphe orienté obtenu corresponde à la matrice $N$.
Modélisation par un graphe
Voici la carte des arrondissements du département de la Marne lors des dernières élections législatives.
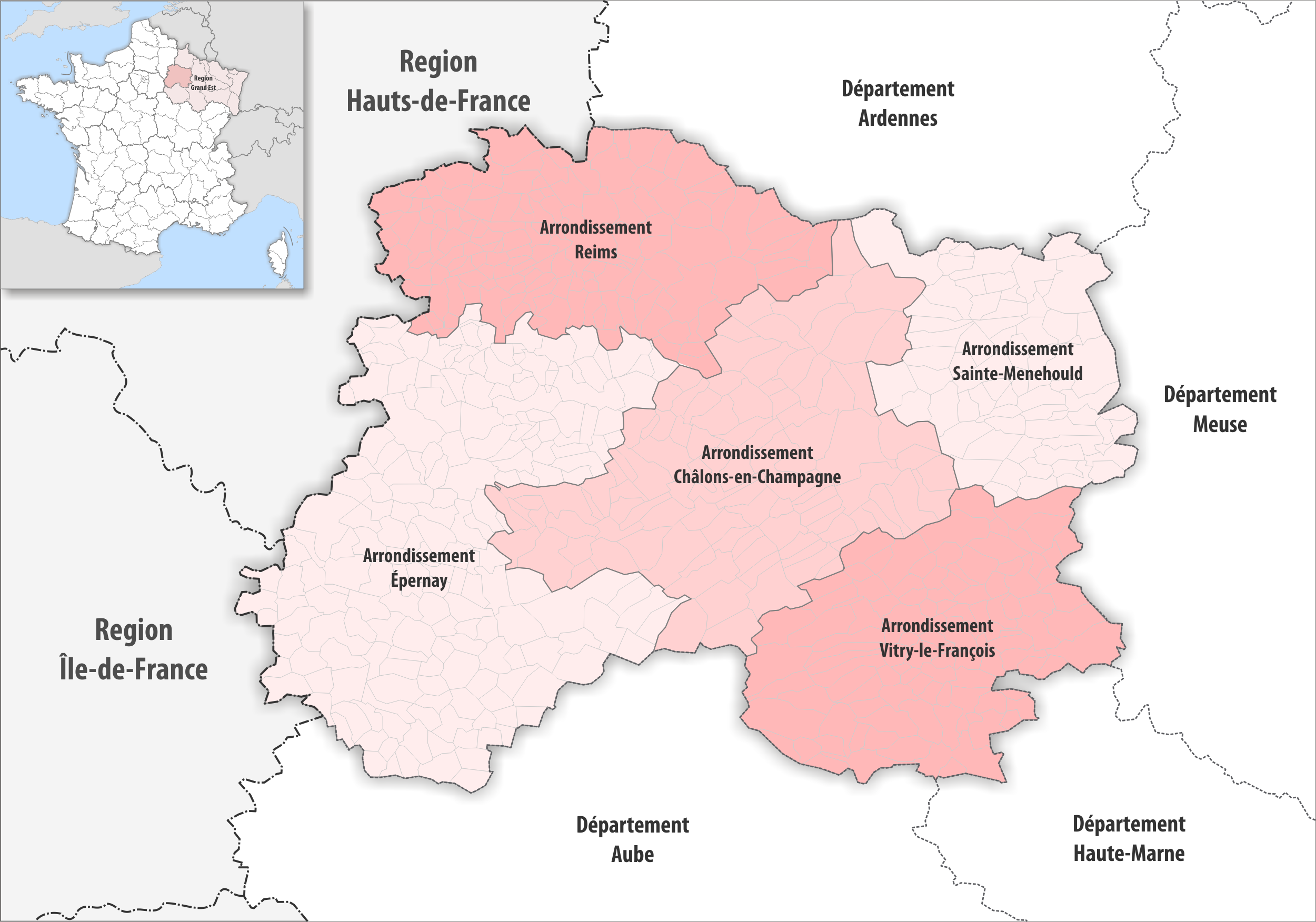
-
Modéliser cette carte des arrondissements par un graphe dans lequel les sommets sont les arrondissements (prendre l'initiale du nom de l'arrondissement comme nom du sommet) et les arêtes traduisent la présence d'une frontière entre deux régions.
-
Le graphe est-il orienté ?
-
Le graphe est-il complet ?
-
Le graphe est-il connexe ?
$P_1$, $P_2$, $P_3$, $P_4$, $P_5$ et $P_6$ désignent 6 espèces de poissons.
Dans le tableau ci-dessous, une croix signifie que deux espèces ne peuvent cohabiter dans le même milieu.
| Espèces de poissons | $P_1$ | $P_2$ | $P_3$ | $P_4$ | $P_5$ | $P_6$ |
|---|---|---|---|---|---|---|
| $P_1$ | X | X | ||||
| $P_2$ | X | X | X | |||
| $P_3$ | X | X | ||||
| $P_4$ | X | X | ||||
| $P_5$ | X | X | ||||
| $P_6$ | X |
-
Le graphe où les sommets sont des espèces de poissons tandis que les arêtes indiquent les incompatibilités entre espèces est-il orienté ou non ? Justifier.
-
Représenter ce graphe.
-
Combien de bassins différents faut-il prévoir au minimum pour pouvoir élever ces 6 espèces de poissons ?
Une classe de Terminale est en voyage scolaire en Angleterre.
Les professeurs organisateurs de ce voyage décident de visiter plusieurs sites de Londres.
Les sites retenus dans Londres sont les suivants : Warren Street, Oxford Circus, Piccadilly Circus, Leicester Square, Holborn, Embankment et Temple. Ces lieux sont désignés respectivement par les lettres $W$, $O$, $P$, $L$, $H$, $E$ et $T$.
Le professeur d'anglais aimerait représenter l'ensemble des sites à visiter avec les jonctions possibles entre eux à l'aide d'un graphe.
Il y a demandé de l'aide à son collègue de mathématiques, qui très taquin, lui a transmis le "tableau de nombres" suivant :
$$ \begin{pmatrix} 0 &0 &0 &0 &1 &1 &0 \\ 0 &0 &1 &0 &0 &1 &1 \\ 0 &1 &0 &0 &1 &1 &1\\ 0 &0 &0 &0 &1 &0 &1\\ 1&0 &1 &1 &0 &1 &0\\ 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &0 &0\\ \end{pmatrix} $$Le professeur de maths lui a aussi dit que :
-
il avait considéré les lettres des sites dans l'ordre alphabétique,
-
qu'il fallait alors considéré le "tableau de nombres" comme la matrice d'adjacence du graphe recherché.
Tout cela est très obscur pour le professeur d'anglais, il est tout déo=sorienté ! Il fait donc appel à vous pour obtenir le graphe recheché.
Construire un graphe correspondant au besoin du professeur d'anglais ; il vous remerciera au moins d'un grand "Thanks a lot !"
Lors d'une soirée chez mes voisins, j'ai entendu 45 tintements de verre.
En supposant que chaque personne a trinqué une et une suele fois avec les autres, déterminer le nombre de personnes présentes.
Un État virtuel compte 11 grandes viles dont la capitale $C$.
Chacune de ces 11 viles est reliée a au moins 5 grandes villes par une autoraute.
Peut-on aller, en emprunant l'autoroute, de la capitale à chacune des autres grandes villes de ce pays ?
On donne ci-dessous le plan simplifié d'un lycée :
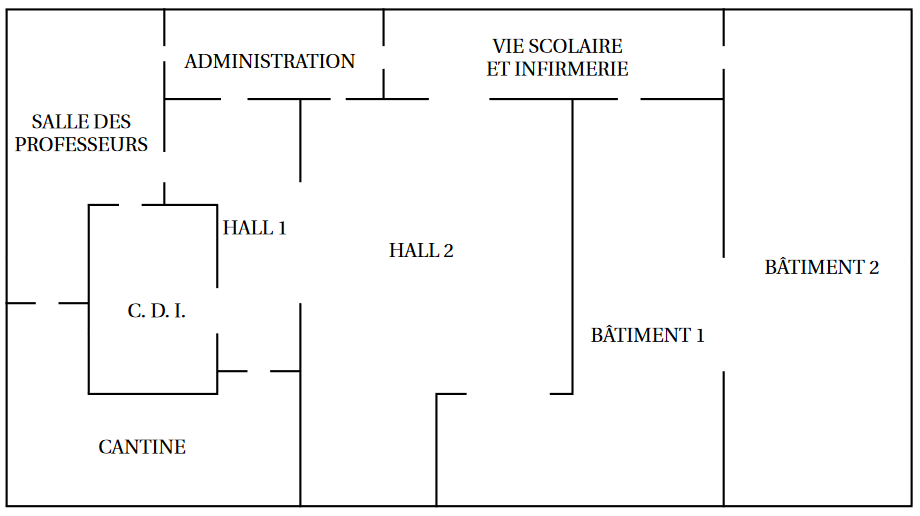
-
Traduire la situation par un graphe dont les sommets représentent les salles et dont les arêtes représentent les passages possibles entre ces salles.
-
Quel est l'ordre du graphe ?
-
Le graphe est-il connexe ? Qu'en déduire concrètement ?
-
Le graphe est-il complet ? Qu'en déduire concrètement ?
À la fin d'un semestre, les examines de licence prposent six options : Calcul différentiel ; Géométrie euclidienne ; Théorie des nombres ; Algèbre linéaire ; Probabilités et Statistiques.
Chacun des candidats a pu choisir deux ou trois de ces options.
Certians ont choisi Théorie des nombres et Algèbre linéaire ; d'autres le Calcul différentiel, les Probabilités et les Statistiques ; enfin d'autres ont choisi Géométrie euclidienne et Théorie des nombres.
Sachant que les étudiants passent au plus une épreuve chaque jour, combien peut-on programmer d'épreuves au maximum en une journée ?
Parmi 11 élèves volontaires, un professeur de mathématiques doit constituer des groupes d'au plus 4 personnes pour faire préparer une présentation orale.
Le professeur doit faire attention aux relations entre les élèves :
-
Erwan ne supporte pas Kenza et n'apprécie ni Gwendoline, ni Blaise, ni Chloé.
-
Jordan refuse de travailler avec Gwendoline,
-
Kenza n'arrive jamais a resté sérieuxe ni avec Aya, ni avec Driss.
-
Blaise a du mal à travailler avec Erwan,
-
Chloé ne supporte ni Jordan, ni Blaise
-
Comme Hector a remplacé Fred dans le coeur d'Ilana, Fred ne veut plus échanger un mot avec Hector ou Ilana.
Comme le professeur de mathématiques n'arrive pas à constituer le minimum de groupes ne dépassant pas 4 élèves, il fait appel à vous :
Combien de groupes ne dépassant pas 4 élèves peut-on faire au minimum ? Proposez une répartition des élèves pour avoir un minimum de groupes.
Exercices de prolongement
Partie A : Conjecture d'un théorème
Une chaîne eulérienne est une chaîne qui contient une fois et une seule chaque arête du graphe.
Concrètement, Chercher une chaîne eulérienne revient à essayer de dessiner le graphe sans lever le crayon et sans passer plus d'une fois sur le même trait
Voici ci-dessous différents graphes :
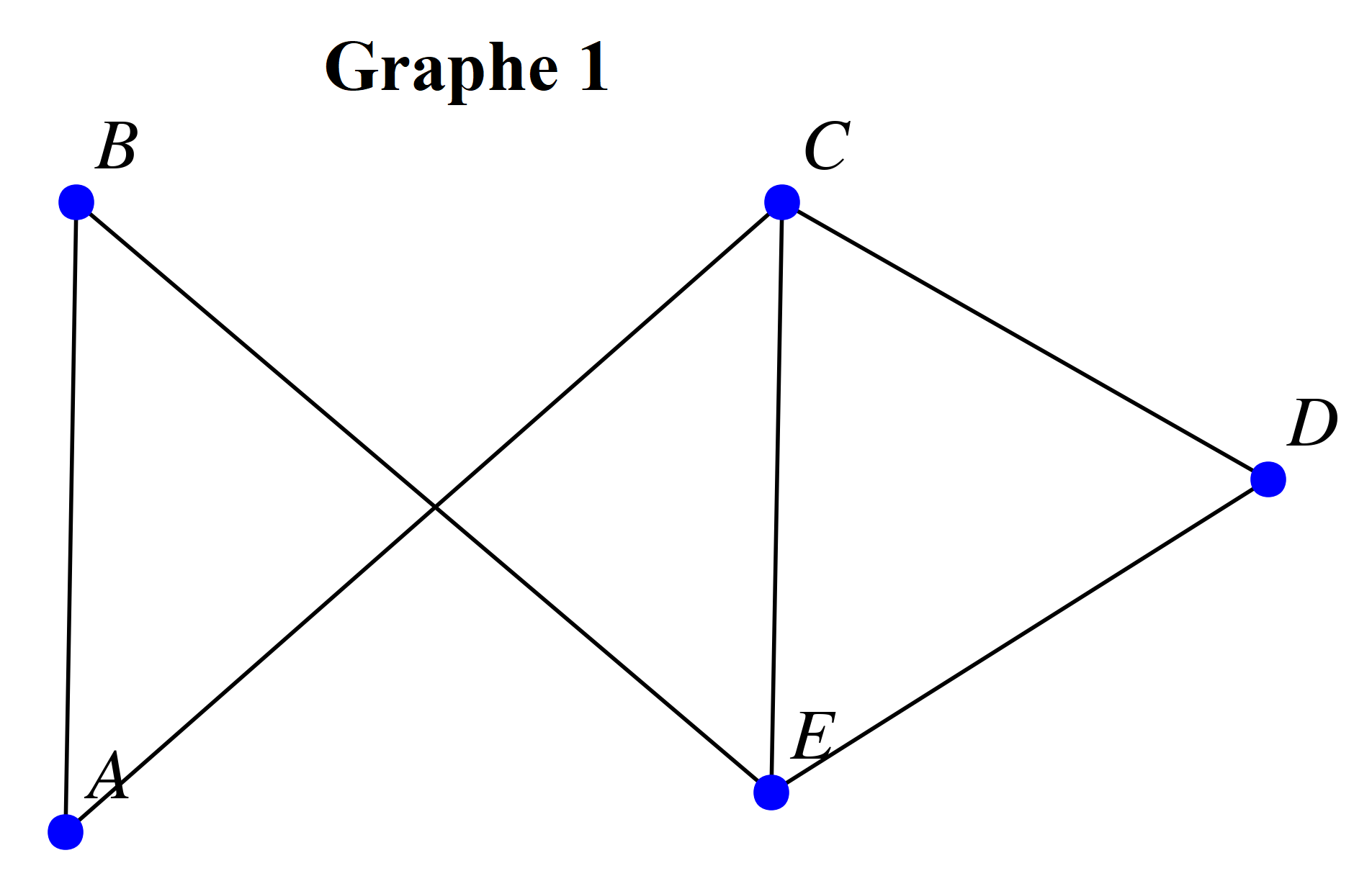
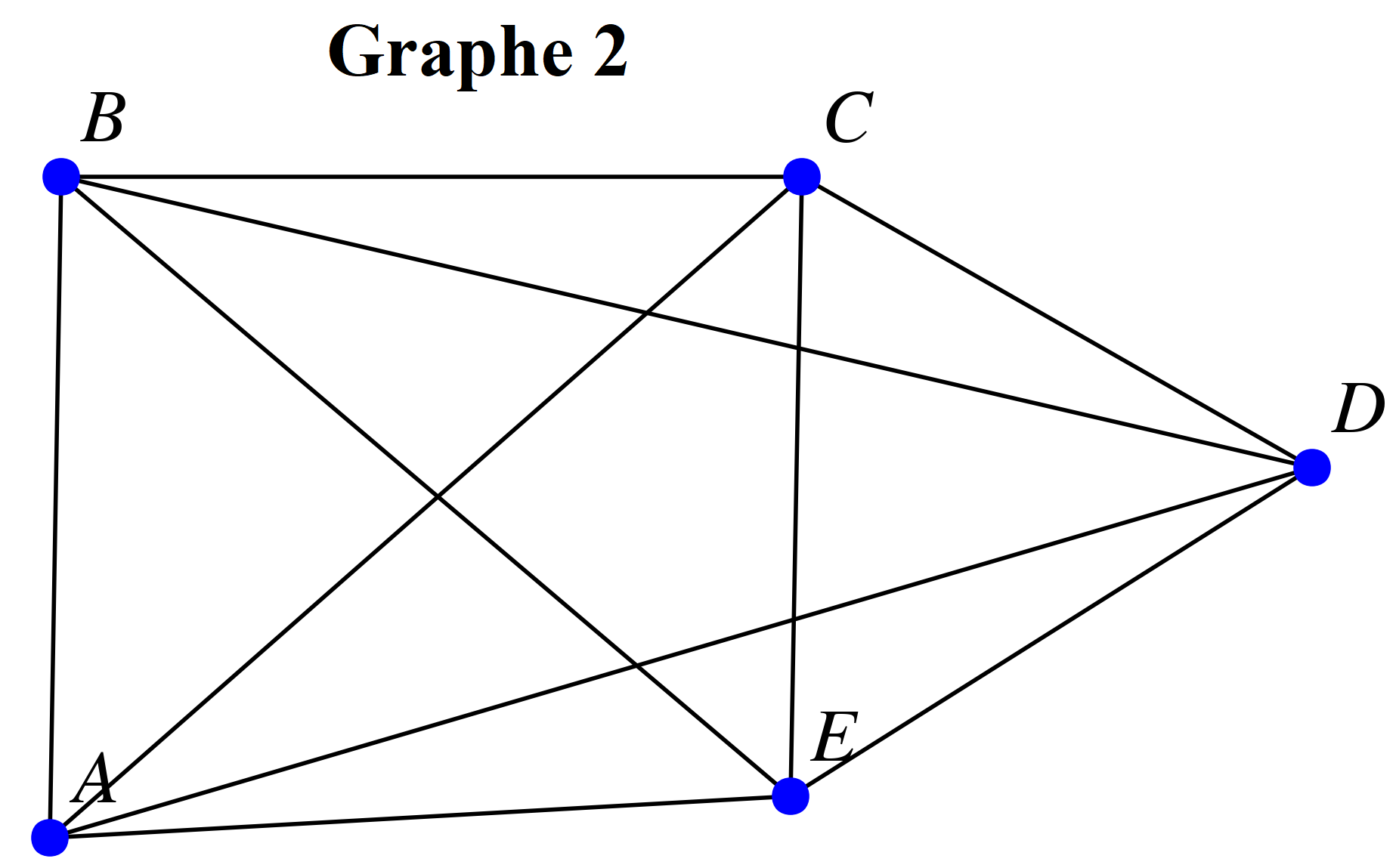
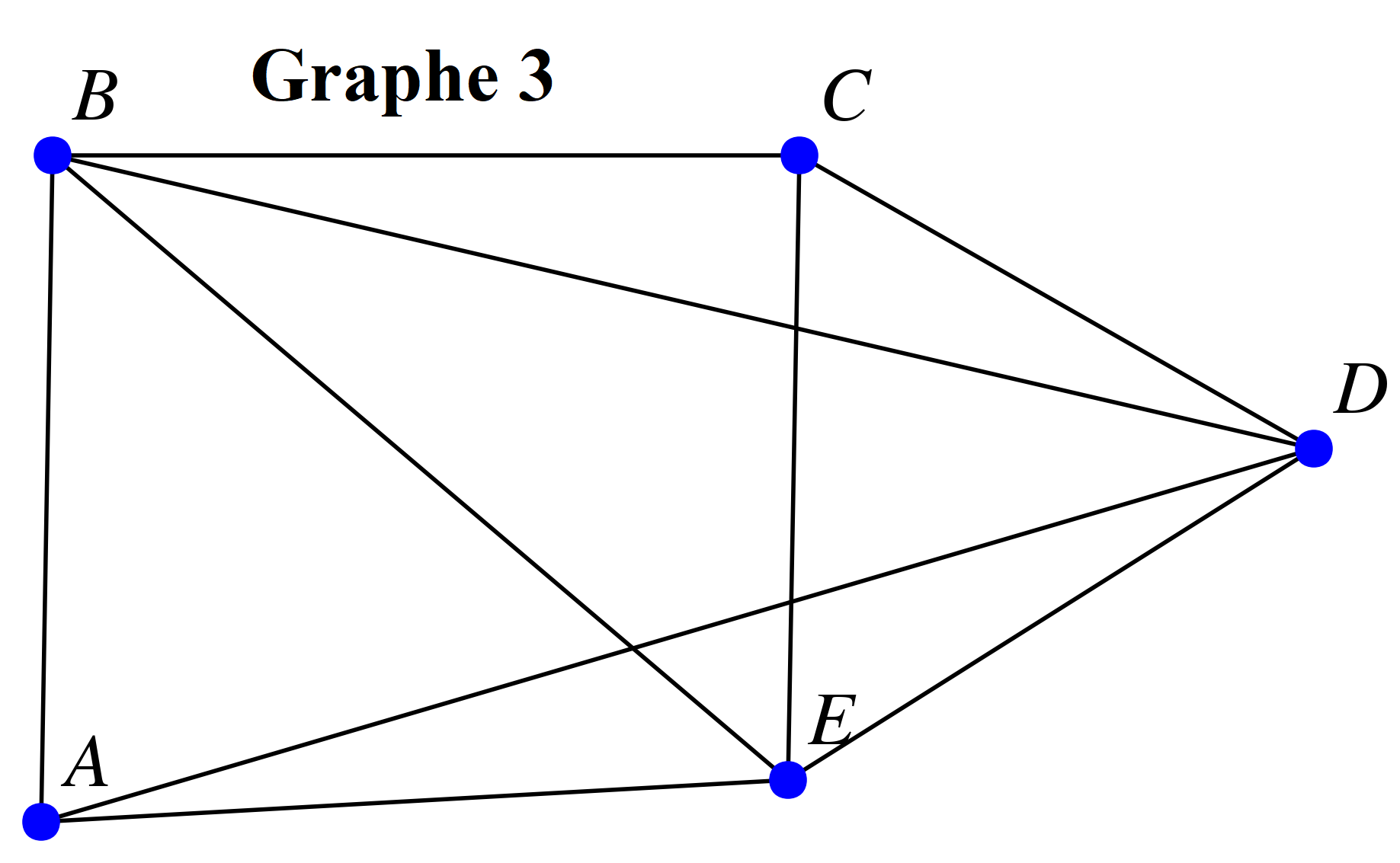
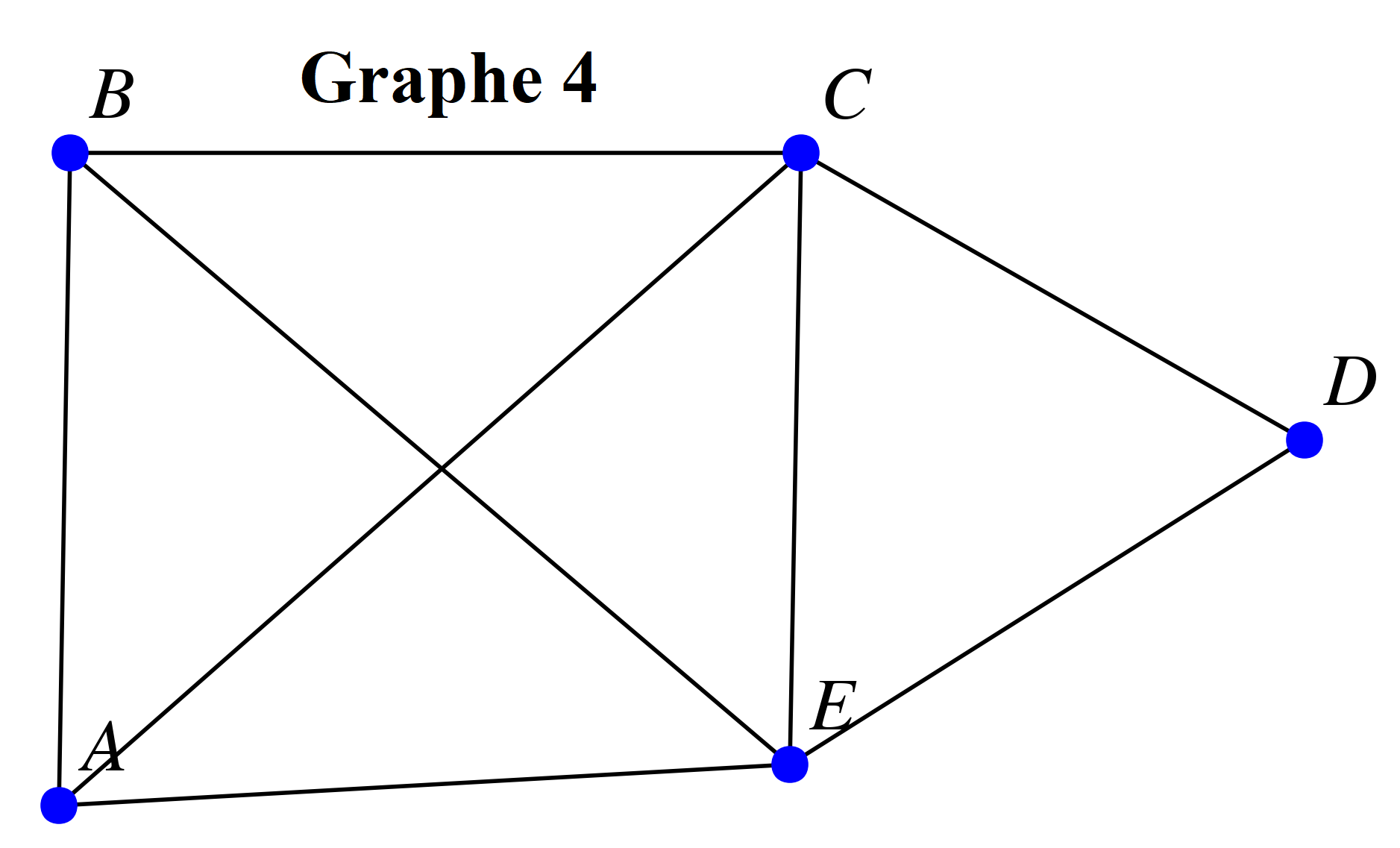
-
Pour chacun des graphes ci-dessus :
-
Chercher si le graphe admet une chaîne eulérienne ou non.
-
Dresser le tableau des degrés du graphe.
-
-
Conjecturer un lien entre l'existence d'une chaîne eulérienne et les degrés du graphe.
Partie B : Application au problème du pont de Königsberg
On considère un graphe contenant une chaîne eulérienne.
-
Expliquer pourquoi tous les sommets sont d'ordre pair, sauf éventuellement le premier et le dernier de la chaîne.
-
On se place dans le cas où les extrémités sont confondues. Considérons un sommet $S$ par lequel la chaîne est passée $k$ fois, $k\in\mathbb{N}$. Quel est le degré de $S$ ?
-
On se place à présent dans le cas où les extrémités ne sont pas confondues? Quel est le degré Quel est le degré d'une extrémité par lequel la chaîne est passée $k$ fois, $k\in\mathbb{N}$ ?
-
Voici un théorème, énoncé par Euler en 1736 et prouvé par Hierholzer en 1873 :
un graphe connexe possède une chaîne eulérienne si, et seulement si, au plus deux de sommets sont de degré impair.
Avec les questions précédentes, a-ton prouvé ce thérème ou non ?
-
Conclure sur le problème des ponts de Königsberg.
Partie A : étude du problème
-
Colorier un graphe, c'est affecter une couleur à chaque sommet, de sorte que deux sommets adjacents ne portent pas la même couleur.
-
Le nombre chromatique, noté $\gamma$, est le plus petit nombre de couleurs nécessaires pour colorier un graphe.
-
Considérons un graphe $\Gamma$.
Un sous-graphe de $\Gamma$ est un graphe $\Gamma'$ composé de certains sommets de $\Gamma$ et de toutes les arêtes reliant ces sommets.
Notons $m$ l'ordre du plus grand des sous-graphes complets de $\Gamma$ et $\Delta$ le plus grand des degré des sommets de $\Gamma$.
Justifier que $m\leqslant \gamma \leqslant \Delta+1$.
Partie B : algorithme de Welh-Powell
Pour colorier un graphe, on peut utiliser l'algorithme glouton suivant :
-
Étape 1 : Ranger les sommets par ordre décroissant de leurs degrés ;
-
Étape 2 : Choisir une couleur ; Affecter cette couleur au premier sommet de la liste non encore coloré ;
-
Étape 3 : Suivre la liste en attribuant cette même couleur à tout sommet :
-
qui n'est pas encore coloré ;
-
et qui n'est pas adjacent à un sommet coloré avec cette couleur.
-
-
Étape 4 : Continuer jusqu'à ce que la liste soit finie :
Si tous les sommets ne sont pas colorés, choisir une couleur qui n'est pas encore utilisée et recommencer les étapes 2 et 3 ;
Continuer tant que chaque sommet n'est pas coloré.
Colorier le graphe ci-dessous à l'aide de cet algorithme :

Partie C : application sur un problème concret
Diogène est éducateur de chiens ; il donne donne des leçons à 9 chiots : Antisthène, Bion, Cléomène, Démétrios, Échéclès, Favonius, Gadarides, Héracléios et Isidore.
Diogène souhaite réaliser des exercices par petits groupes, de 2 ou 3 chiots tout en respectant la nature de ces animaux :
-
Favonius ne pense qu'à jouer si ce chiot est trop proche de Bion, Cléomène ou d'Échéclès,
-
Démétrios est très distrait si Bion et Favonius sont à proximité,
-
Isidore ne supporte pas le caractère trop fougueux de Gadarides,
-
Antisthène ne tolère que la présence d'Échéclès et d'Héraclios.
-
Représenter cette situation à l'aide d'un graphe $\Gamma$.
-
Le graphe est-il connexe ? Justifier.
-
-
Déterminer un sous-graphe complet d'ordre maximal du graphe $\Gamma$.
-
Que peut-on en déduire pour le nombre chromatique du graphe $\Gamma$ ?
-
-
Doner la valeur du nombre chromatique du graphe $\Gamma$.
-
Peut-on proposer une répartition des chiots en groupes de deux ou trpois chiots pouvant travailler ensemble ?
Savoirs et savoirs-faire
-
le vocabulaire sur les graphes non-orientés (ordre, sommets adjacents, degré, chaîne, longueur, connexe, complet),
-
le vocabulaire sur les graphes orientés (arc, degré),
-
la notion de matrice d'adjacence.
-
modéliser un problème concret à l'aide d'un graphe,
-
écrire la mtrice d'adjacence associée à un graphe.

NSI de Auteurs : Thomas Lourdet, Johan Monteillet, est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.