Les phénomènes où apparaît le hasard peuvent être étudiés grâce aux probabilités. La fiabilité d’un objet ou d’un système sont de tels phénomènes.
Exemple introductif
Un élève répond au hasard aux questions d’un Q.C.M. Pour chaque question, quatre réponses dont une seule est exacte. $X$ est la variable aléatoire égale au nombre de bonnes réponses.
-
Si le QCM est constitué d'une seule question, on peut modéliser l'expérience de répondre à ce QCM par un arbre de probabilité comme celui-ci :
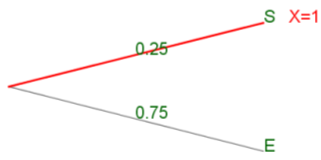
-
Si le QCM est constitué de deux questions, on peut modéliser l'expérience de répondre à ce QCM par un arbre de probabilité comme celui-ci :
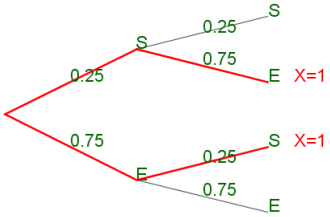
-
Dans le cas où le QCM possède une seule question, quelle est la probabilité d'obtenir une bonne réponse ? (s'aider de l'arbre explicité dans l'exemple ci-dessus).
-
On considère le cas où le QCM possède deux questions.
-
Quelle est la probabilité d'obtenir l'issue $(Succès ; Echec)$ ?
-
Quelle est la probabilité d'obtenir exactement 1 bonne réponse, ce qui se note $P(X=1)$ ?
-
-
On considère le cas où le QCM possède trois questions.
-
Modéliser l'expérience de répondre à ce QCM par un arbre de probabilité.
-
Quelle est la probabilité d'obtenir l'issue $(Echec ; Succès ; Echec)$ ?
-
Quelle est la probabilité d'obtenir exactement 1 bonne réponse, ce qui se note $P(X=1)$ ?
-
Que signifie $P(X=2)$ ?
Que vaut $P(X=2)$ ?
-
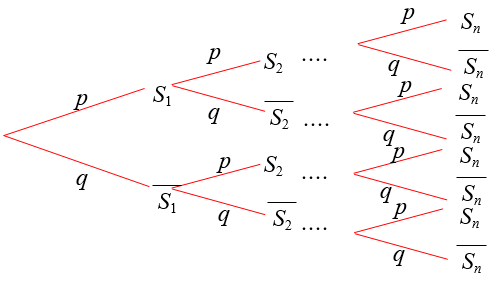
Le problème est que le raisonnement sur ce type d'arbre devient vite ingérable dans le cas où le nombre de questions devient assez grand.
Par exemple, pour $n=8$ l'arbre ci-dessous est illisible et inutilisable pour calculer $P(X=2)$ :
image issue du fichier Geogebra réalisé par M. Créach disponible à
cette adresse.
Il est nécessaire de conceptualiser cette idée d'arbres de probabilité en réfléchissant à ce que l'on fait lorsque l'on construit un arbre de probabilité.
Épreuve et schéma de Bernoulli
Pour construire l'arbre précédent illustrant tout un QCM, on commence par étudier la première question avec deux possibilités, d'où la première défininion :
Une épreuve de Bernoulli est une expérience aléatoire qui ne comporte que deux issues appelées
succès (noté $S$) et échec (noté $\overline{S}$), de probabilités respectives $p$ et $q=1 – p$.
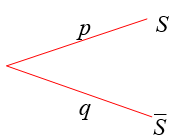 La loi de probabilité ce cette expérience est appelée loi de Bernoulli de paramètre $p$.
La loi de probabilité ce cette expérience est appelée loi de Bernoulli de paramètre $p$.
On considère un QCM ayant 4 questions dont une seule est correcte.
Répondre au hasard à ce QCM est une expérience aléatoire qui ne comprote que deux issues :
-
le "succès" : répondre correctement, de probabilité $\dfrac{1}{4}$,
-
l'"échec" : répondre faussement, de probabilité $\dfrac{3}{4}$.
Répondre au hasard à ce QCM est donc une épreuve de Bernoulli de loi de paramètre $\dfrac{1}{4}$.
Justifier qu'obtenir un 4 lors d’un lancer d’un dé cubique est une épreuve de Bernoulli dont le paramètre de la loi est à préciser.
Le nom d'épreuve de Bernoulli vient du fait que ceci a été développé par Jacques Bernoulli un mathématicien et physicien suisse du XVIIe siècle.
Une fois le premier niveau d'embranchements de l'arbre effectué, il faut réaliser les autres embranchements. Comme les événements et les probabilités sont les même pour chacune des branches, il suffit de répéter pour chaque embranchement l'épreuve de Bernoulli précédente, d'où la définition suivante :
Un schéma de Bernoulli est une expérience aléatoire qui consiste à répéter $n$ fois, dans des conditions indépendantes la même épreuve de Bernoulli dont la probabilité de succès est notée $p$.
Répondre au hasard à un QCM de 10 questions ayant 4 réponses possibles dont une seule est correcte est un schéma de Bernoulli.
En effet, il y a une répétition 10 fois de manière indépendante à l'épreuve Bernoulli consistant à répondre
à une question par la choix au hasard d'une réponse possible parmi les 4 proposées.
Une entreprise fabrique un très grand nombre de câbles coaxiaux.
L’entreprise étudie régulièrement le nombre de câbles coaxiaux produits de qualité ainsi que le nombre de pannes
survenant sur la machine-outil permettant la fabrication de ces câbles.
Ces études ont montré que :
-
la qualité de chaque câble coaxial produit est indépendante de celles des autres câbles coaxiaux déjà produits et que la probabilité qu'un câble coaxial prélevé au hasard soit de qualité est de 0.973.
-
une panne arrive sur une machine-outil indépendamment des autres pannes déjà rencontrées. En moyenne, il y a 4 jours sur 100 où cette machine-outil tombe en panne.
-
L'entreprise emploie 100 peronnes dont 40 femmes.
Pour chacune expérience aléatoire suivante, préciser si elle correspond ou non à un schéma de Bernoulli. Justifier.
-
L'étude du nombre de câbles coaxiaux de qualité sur un prélèvement de 100 câbles.
-
L'étude du nombre de jours sur une durée de 100 jours consécutifs où la machine-outil tombe en panne.
-
L'entreprise décide chaque jour de mettre en avant un.e employé.e. Ainsi, sur chaque période de 100 jours ouvrés, elle tire au sort un.e salarié.e de l'entreprise qui se voit alors valoriser devant toute l'équipe et aussi financièrement. Pour des questions d'équité, une fois un.e salarié.e sélectionné.e, iel ne peut plus être tirée au sort : ainsi chaque employé.e sera valorisé.e une fois au cours de chaque période de 100 jours ouvrés.
On considère ainsi l'expérience aléatoire correspondant à l'étude du nombre de femmes salariées valorisées sur les 30 premiers jours ouvrés. Est-ce un schmé de Bernoulli ? Pourquoi ?
Loi binomiale
Définition et rédaction
On considère une expérience aléatoire à deux issues $S$, de probabilité $p$, et $\overline{S}$, de probabilité $q=1-p$.
On répète $n$ fois de suite cette expérience aléatoire de façons indépendantes.
Soit $X$ la variable aléatoire comptabilisant le nombre de fois où $S$ est réalisée lors de ces $n$ expériences.
On dit que $X$ suit la loi binomiale de paramètres $n$ et $p$.
Cette loi est notée $\mathcal{B}(n;p)$.
Lancer 20 fois de suite le même dé est un schéma de Bernoulli car chaque lancer est identique et indépendant.
Soit $X$ la variable aléatoire donnant le nombre de fois où le 4 sort.
$X$ suit la loi binomiale de paramètres $n=20$ et $p=\dfrac{1}{6}$.
Rédaction attendue à chaque fois :
Vous pouvez modifier les phrases suivantes et l'adapter à chaque question concrète, mais :
-
les éléments en gras sont nécessaires,
-
les phrases en italique ne sont pas à reproduire : elles ne servent qu'à comprendre que la rédaction revient à décrire comment dessiner un arbre de probabilité avec de nombreuses répétitions.
On commence par le premier embranchement :
Pour chaque lancer, il y a deux issues possibles :
-
le succès : "le nombre 4 est obtenu", de probabilité $p=\dfrac{1}{6}$.
-
l'échec : "le nombre 4 n'est pas obtenu", de probabilité $q=1-\dfrac{1}{6}=\dfrac{5}{6}$.
On explique comment procéder pour les autres embranchements :
On répète ceci 20 fois dans des conditions où sont données les réponses sont identiques et indépendantes.
On explique ce que l'on regarderait sur l'arbre de probabilité :
$X$ comptabilise le nombre de succès, donc X suit la loi binomiale de paramètres $n=20$ et $p=\dfrac{1}{6}$, soit $\mathcal{B}(20;16)$.
On considére une entreprise fabriquant des commutateurs (switches). On admet que 0.4% des commutateurs sont
non fonctionnels.
Un envoi de 800 commutateurs est prévu : 800 commutateurs sont prélevés du stock produit.
La production est assez importante pour que l’on puisse assimiler ce prélèvement à un tirage avec remise.
On considère la variable aléaroite $X$ qui, à tout prélèvement de 800 commutateurs, associe le nombre de commutateurs non fonctionnels.
Déterminer rigoureusement la loi de probabilité suivie par $X$.
Utilisation de Geogebra
En BTS, il est essentiel de savoir utiliser Geogebra pour calculer des probabilités liées à la loi binomiale.
Voici la méthode à suivre :
-
Lancer le module Calculs de probabilités de Geogebra :
-
soit choisir au niveau de l'onglet ABC la ligne Calculs de probabilité.
-
soit cliquer au démarrage sur Calculs de probabilité.
-
soit cherche dans le menu affichage l'onglet Calculs de probabilité.
-
-
Apparaît alors une fenêtre comme celle ci-dessous :
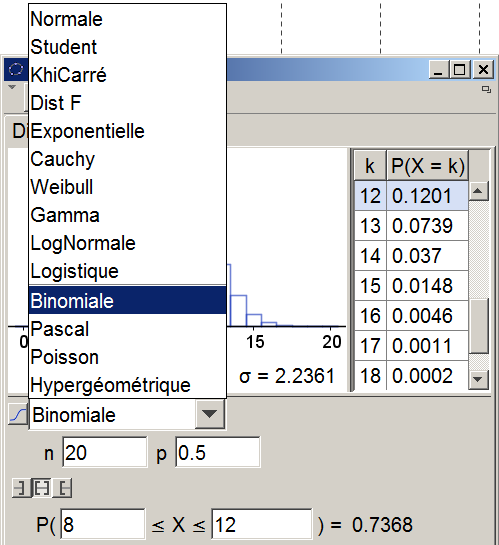
En choisissant Binomiale dans le menu déroulant, puis en réglant les paramètres $n$ et $p$, vous pourrez faire obtenir toutes les probabilités désirées. -
Par exemple, pour travailler avec la loi binomiale de paramètres $n=20$ et $p=0.3$, on obtient l'affichage suivant :
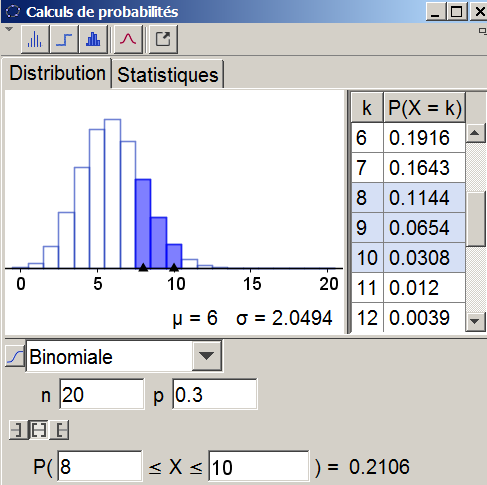
Cet affichage permet de :-
visualiser la représentation graphique de cette loi binomiale (zone supérieure gauche),
-
connaître la valeur de chaque probabilité $P(X=k)$ (colonne de droite),
-
visualiser une valeur approchée de l'espérance $\mu$ et de l'écart-type $\sigma$ (cf. partie 4 ) de cette loi binomiale (coin inférieur droit de la zone graphique),
-
calculer la valeur de chaque probabilité de la forme $P(X\le k)$ ou $P(a\le X\le b)$ ou $P(k\le X)$ (dernière ligne).
La probabilité calculée est représentée aussi graphiquement comme partie colorée de l'histogramme.
-
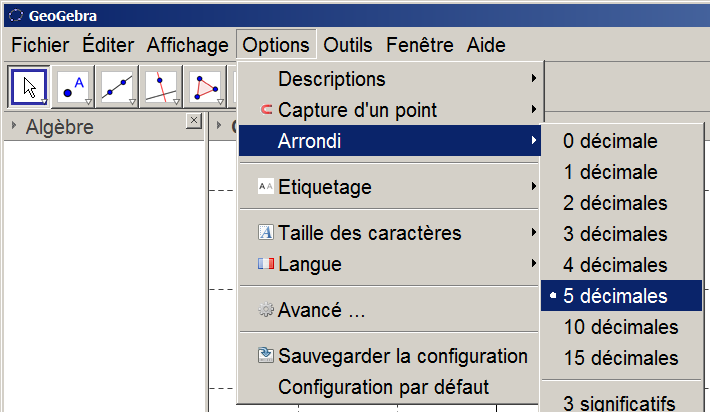
$X$ suit la loi binomiale de paramètres $n=123$ et $p=0.14$.
On veut obtenir la probabilité arrondie à $10{-5}$ près de $P(X\ge 35)$.
Pour cela, il suffit de :
-
modifier la précision de l'affichage dans Options, puis Arrondi.
-
Sélectionner la loi binomiale puis préciser la valeur de chaque paramètre,
-
Sélectionner la zone correspondant à $...\le X$ puis préciser la valeur de la borne.
-
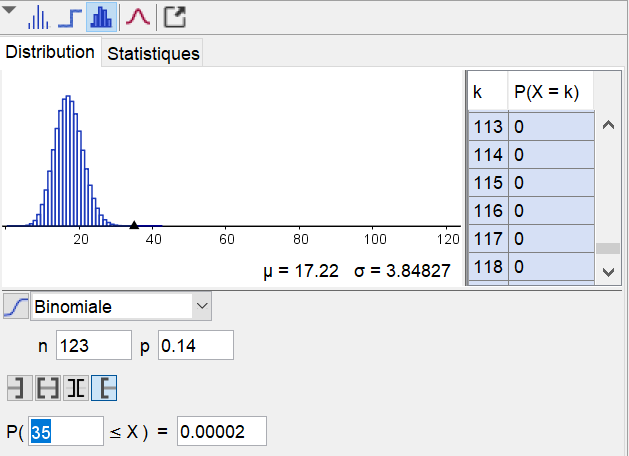
Lire la valeur affichée pour la probabilité choisie.
Ici, on obtient ainsi, $P(X\ge 35) \approx 0.00002$.
On considère un stock important de clé USB d'une entreprise d'import/export de matériel informatique.
On admet que dans ce stock 2 % des clés USB ne sont pas acceptables.
On prélève au hasard 260 clés USB de ce stock.
Le stock est suffisamment important pour que l’on puisse assimiler ce prélèvement à un tirage avec
remise de 260 clés USB.
On note $Y$ la variable aléatoire qui, à tout prélèvement de 260 clés USB, associe le nombre
d’entre elles qui ne sont pas acceptables.
-
Justifier que la variable aléatoire $Y$ suit une loi binomiale dont on déterminera les paramètres.
-
Calculer la probabilité qu’au plus quatre clés ne soient pas acceptables dans le prélèvement.
-
Calculer la probabilité que plus de huit clés ne soient pas acceptables dans le prélèvement.
-
Calculer la probabilité que le prélèvement contiennent sept clés non acceptables.
-
Calculer la probabilité que le prélèvement contiennent entre trois et neuf clés non acceptables.
-
Un lot similaire de 260 clés doit être acheminé à un client.
Les clauses de qualité stipulent que ce client sera remboursé de l'intégralité du lot envoyé si ce lot contient au moins 8 % de clés USB non acceptables.
Déterminer la probabilité que l'entreprise d'import/export doive rembourser l'intégralité du lot de 260 clés USB envoyé.
Espérance, variance et écart-type
Espérance
Un élève répond au hasard aux questions d’un Q.C.M.
Pour chaque question, quatre réponses dont une seule est exacte. $X$ est la variable aléatoire égale au nombre de bonnes réponses.
-
Si le QCM est constitué de 4 questions, combien de réponses en moyenne peut-on espérer comme bonnes ?
-
Si le QCM est constitué de n questions, combien de réponses en moyenne peut-on espérer comme bonnes ?
Ce nombre est appelé l'espérance mathématiques de $X$ et est noté $E[X]$. -
Un QCM est constitué de 10 questions. Le concepteur teste son QCM en faisant répondre au hasard par un ordinateur à ses 10 questions.
Il répète $m$ fois ce test et calcule la moyenne des bonnes réponses sur ces $m$ tests. Il obtient le tableau suivant :

Est-ce que l'espérance mathématique correspond à la moyenne de bonnes réponses que l'on peut espérer en répétant un très grand nombre de fois ?
L'espérance mathématique d'une variable aléatoire $X$ qui prend $n$ valeurs $x_i$ avec des probabilités $P(X=x_i)$ est le nombre $E[X]=x_1\times P(X=x_1)+x_2\times P(X=x_2)+x_3\times P(X=x_3)+ .... +x_n \times P(X=x_n)$, ce qui se note : $\displaystyle E[X]=\sum _{k=0}^{n} x_k\times P(X=x_k)$.
L'espérance $E[X]$ peut être interprétée comme tendance à long terme de la valeur moyenne observée $\overline{x}$ dans le cas d'un très grand nombre de réalisations du schéma de Bernoulli associé à la variable aléatoire $X$.
L'espérance mathématique d'une variable aléatoire suivant une loi binomiale $\mathcal{B}(n;p)$ est $n\times p$.
Ce qui se note : $E[\mathcal{B}(n;p)]=n\times p$.
Variance et écart-type
Soit une variable aléatoire $X$ qui prend $n$ valeurs $x_i$ avec des probabilités $P(X=x_i)$. On note $E[X]$ son espérance mathématique.
-
La variance de $X$ est le nombre : $V[X]=(x_1-E[X])^2\times P(X=x_1)+(x_2-E[X])^2\times P(X=x_2)+(x_3-E[X])^2\times P(X=x_3)+ .... +(x_n-E[X])^2 \times P(X=x_n)$, ce qui se note :
$\displaystyle V[X]=\sum _{k=0}^{n} (x_k-E[X])^2\times P(X=x_k)$.La variance est la moyenne des carrés des écarts entre la moyenne et chaque valeur : c'est un indice de la dispersion des valeurs autour de la moyenne : plus la variance est faible, plus les valeurs sont proches de la moyenne.
-
L’écart-type de $X$ est le nombre $\sigma(X)=\sqrt{V(X)}$.
L'écart-type est comme la variance un indice de la dispersion des valeurs autour de la moyenne : plus l'écart-type est faible, plus les valeurs sont proches de la moyenne.
La variance d'une variable aléatoire suivant une loi binomiale $\mathcal{B}(n;p)$ est $n\times p\times (1-p)$.
Ce qui se note : $V[\mathcal{B}(n;p)]=n\times p\times (1-p)$.
L'écart-type d'une variable aléatoire suivant une loi binomiale $\mathcal{B}(n;p)$ est $\sqrt{n\times p\times (1-p)}$.
Ce qui se note : $\sigma[\mathcal{B}(n;p)]=\sqrt{n\times p\times (1-p)}$.
Geogebra affiche dans le coin inférieur droit de la zone graphique la valeur approchée de l'espérance mathématique sous la forme la lettre $\mu$ et de l'écart-type sous la lettre $\sigma$.
Un lecteur MP3 contient 70% de titres anglais et 30% de titres français.
On crée au hasard une playlist de 20 morceaux (avec possibilité de répéter plusieurs fois le même titre).
$X$ compte le nombre de titres français dans la playlist.
-
Justifier que la loi de probabilité de $X$ est une loi binomiale dont les paramètres sont à préciser.
-
Quelle est la probabilité d’obtenir au moins 7 titres français dans cette playlist ?
-
Déterminer le nombre moyen de titres français de cette playlist.
-
Déterminer l'écrt-type $\sigma(X)$ du nombre de titres français.
-
Déterminer la probabilité que le nombre de titres français soit compris entre $E[X]-\sigma(X)$ et $E[X]+\sigma(X)$.
Propriété de linéarité
-
Si j'augmente de 1 chacune des notes obtenues au devoir précédent, comment évoluera la moyenne de classe obtenue à ce devoir ?
-
Si je mutilplie par 2 chacune des notes obtenues au devoir précédent, comment évoluera la moyenne de classe obtenue à ce devoir ?
-
Si j'augmente de 1 chacune des notes obtenues au devoir précédent, comment évoluera la variance (=dispersion) de classe obtenue à ce devoir ?
-
Si je mutilplie par 2 chacune des notes obtenues au devoir précédent, comment évoluera la variance (=dispersion) de classe obtenue à ce devoir ?
Pour tout réel $a$ et $b$, on a :
-
$E[aX+b]=aE[X]+b$.
-
$V[aX+b]=a^2\times V[X]$.
À un jeu de hasard, la probabilité de gagner est de 0.0001. Chaque semaine, on peut jouer à ce jeu.
On admet que le fait de gagner ou de perdre une semaine donnée de dépend pas du résultat des semaines précédentes.
On note $X$ la variable aléatoire comptabilisant le nombre de victoires du joueur sur une année.
-
On admet que $X$ sui une loi binomiale. Préciser les paramètres de cette loi.
-
On admet qu'à ce jeu, on peut participer pour une mise de 2€ et que l'on peut gagner 8000€ en cas de victoire.
On note $Y$ la variable aléatoire donnant le bilan algébrique financier du joueur sur une année (bilan=gain-dépenses).-
Justifier que $Y=8000X-104$.
-
Pensez-vous qu'il serait intéressant que vous jouiez à ce jeu ou non ? Pourquoi ?
-
Exercices
Arbre pondéré
Des plats cuisinés d'un certain type sont fabriqués en grandes quantités.
On prélève au hasard un plat d'un lot dans lequel 97 % des plats sont conformes au cahier des charges.
On remet le plat dans le lot et on effectue un deuxième prélèvement d'un plat.
On répète une troisième fois l'expérience. On a réalisé trois prélèvements d'un plat avec remise.
-
Construire un arbre pondéré schématisant les prélèvements.
-
Calculer la probabilité de l'événement $C$: "deux des trois plats prélevés sont conformes au cahier des charges".
Utilisation de Geogebra
-
-
Utiliser Geogebra afin de représenter la loi binomiale de paramètres $n=20$ et $p=0.5$ à l'aide d'un diagramme en bâtons.
-
Quelle propriété possède le diagramme pour $p=0.5$ ?
-
Comparer l'allure des diagrammes lorsque $p=0.1$, $p=\dfrac{1}{3}$ et $p=0.9$.
-
-
Pour $n=100$, comparer l'allure des diagrammes lorsque $p=0.1$ et $p=0.01$.
Propriétés de linéarité
Deux amis jouent à un jeu. Le premier lance deux dés équilibrés.
On compte la somme des deux dés. Si cette somme dépasse ou égale 10, le premier joueur gagne le jeu.
-
Prouver que la probabilité que le premier joueur gagne est de $\dfrac{1}{6}$.
-
Les deux amis décident de répéter ce jeu 40 fois.
On note $X$ la variable aléatoire comptabilisant le nombre de victoire du premier joueur.-
Déterminer la loi de probabilité suivie par $X$.
-
Quelle est la probabilité que le premier joueur gagne exactement 10 parties ?
-
Quelle est la probabilité que le premier joueur gagne au moins la moitié des 40 parties ?
-
Combien de parties gagne au maximum le premier joueur dans au moins la moitié des cas ?
-
-
Les deux amis décident de modifier le jeu. A chaque victoire du premier joueur, il gagne 11€, à chaque défaite, il perd 2€.
On note $Y$ la variable aléatoire donnant le gain du premier joueur sur les 40 parties.-
Justifier que $Y=13X-80$.
-
Déterminer l'espérance et la variance de $Y$.
-
Conseilleriez-vous au premier joueur de jouer à ce jeu ou non ? Pourquoi ?
-
Dans cet exercice, tous les résultats seront arrondis à $10^{-3}$ près.
Un représentant d'une société de conseil en sécurité informatique démarche dix clients par jour.
On suppose que chaque client lui signe un contrat de sécurité avec une probabilité de 0.05 et que chaque client
prend la décision de signer ou non un tel contrat, sans être influencé par le comportement des autres clients
-
Calculer la probabilité, pour le représentant, de faire signer un jour donné :
-
au moins un contrat de sécurité,
-
exactement trois contrats.
-
-
Sachant que le représentant touche 100 euros de commission pour chaque signature, calculer la probabilité qu'il gagne au moins 200 euros en une journée.
-
Quelle est, en moyenne, la somme totale des commissions gagnées en une journée ?
Une entreprise produit des objets qu'elle vend en réalisant un bénéfice de 10€ pièce si cet objet est correct.
L'entreprise indemnise ses clients avec 30€ par pièce non conforme livrée.
On considère que la probabilité qu'une pièce produite, choisie au hasard, ne soit pas conforme est de 0.02.
L'entreprise prélève pour livraison 200 objets de sa production. On considère que la production est assez importante pour
assimiler ce prélèvement à un tirage avec remise de 200 objets.
On note $X$ la variable aléatoire comptant le nombre de pièces correctes sur cette livraison de 200 pièces et
$Y$ la variable aléatoire donnant bénéfice réalisé par cette livraison.
Déterminer le bénéfice que peut espérer l'entreprise lors de cette livraison.
loi binomiale
On s'intéresse aux requêtes reçues par le serveur Web d'une grande entreprise, provenant de clients dispersés sur le réseau
Internet. La réception de trop nombreuses requêtes est susceptible d'engendrer des problèmes de surcharge de serveur.
On considère :
-
d'une part, que la probabilité pour le serveur de connaître des dysfonctionnements importants au cours d'une journée donnée est $p=0.01$,
-
d'autre part, que les dysfonctionnements importants survenant au cours de journées distinctes constituent des événements aléatoires indépendants.
On désigne par $X$ la variable aléatoire qui, à tout mois de 30 jours choisi au hasard, associe le nombre de jours où le serveur connaît des dysfonctionnements importants.
-
Justifier que la variable aléatoire $X$ suit une loi binomiale et préciser les paramètres de cette loi.
-
Déterminer la probabilité que le serveur connaisse au plus 2 jours de dysfonctionnements importants pendant un mois.
-
Déterminer, sur un mois de 30 jours, le nombre de jours où, en moyenne, le serveur connaisse des dysfonctionnements importants.
extraits ou modifications de sujets de BTS
Les ateliers de peinture d'un grand constructeur automobile fonctionnant à l'aide de robots permettant de positionner
les pistolets autour de la carrosserie.
Les pannes mécaniques sur le bras articulé de ces robots, assez fréquentes, sont souvent sans gravité.
Elles sont généralement dues à l'encrassage par la peinture (événement $E$) , à du jeu ou à un blocage dans les
articulations mécaniques (événement $M$).
Les ateliers de peinture comptent 100 robots équipés de bras articulés identiques dont les pannes mécaniques
surviennent de façon indépendante. Pour chaque bras articulé, la probabilité, qu'une semaine choisie au hasard,
de l'événement encrassage $E$ est de 0.05 et celui de l'événement $M$ est de 0.02.
-
Justifier que la probabilité, qu'une semaine donnée, un bras articulé subisse une panne mécanique (événement $A$) est de 0.069.
-
Justifier que $X$ suit une loi binomiale dont les paramètres seront à préciser. (rédiger les phrases attendues)
-
Déterminer une valeur approchée arrondies à $10^{-3}$ près des probabilités suivantes :
-
$P(X=2)$.
-
$P(X\lt 4)$.
-
$P(X\ge14)$.
-
$P(2\le X\le 8)$.
-
$P(B)$ où $B$ est l'événement "en une semaine, strictement plus de 10 robots ont connu une panne mécanique sur leur bras articulé".
-
-
-
Déterminer l'espérance de la variable aléatoire X.
-
Interpréter concrètement le résultat.
-
Une semaine étant choisie au hasard, on réalise, pour chacun des 100 robots, la même expérience aléatoire constituant
à observer si son bras connaît une défaillance mécanique.
On désigne par $X$ la variable aléatoire qui, à toute semaine, associe le nombre de robots dont le bras a connu une panne.
Une usine fabrique des moteurs électriques. Afin de vérifier la conformité des moteurs, on procède à deux tests : l’un
de type mécanique, l’autre de type électrique.
Un moteur est déclaré parfait état de marche s’il ne présente aucun des deux défauts ; il est rejeté sinon.
Une étude statistique de la production conduit à admettre que :
-
la probabilité qu’un moteur soit défectueux pour le test mécanique est de 0.08,
-
la probabilité qu’un moteur soit défectueux pour le test électrique est de 0.05,
-
la probabilité qu’un moteur soit défectueux pour les deux tests est de 0.02.
On prélève au hasard un moteur dans la production. On appelle $D_M$ l’événement : "le moteur présente un défaut de type mécanique" et $D_E$ l’événement : "le moteur présente un défaut de type électrique".
-
-
Les événements $D_E$ et $D_M$ sont-ils indépendants ?
-
Calculer la probabilité de l’événement $D_M$ sachant que l’événement $D_E$ est réalisé.
-
-
-
Calculer la probabilité de l’événement $A$ : "le moteur prélevé présente au moins un défaut".
-
Démontrer que la probabilité de l’événement B : "le moteur prélevé est en parfait état de marche" est 0.89.
-
Déterminer la probabilité de l’événement C : "le moteur prélevé présente un seul défaut".
-
-
-
Justifier que la variable aléatoire $Y$ suit une loi binomiale dont on donnera les paramètres.
-
Calculer la probabilité de l’événement "il y a au moins 10 moteurs en parfait état de marche".
On prélève 12 moteurs au hasard dans la production (on assimile cette épreuve à un tirage de 12 pièces successivement avec remise). Soit $Y$ la variable aléatoire qui, à chaque prélèvement de 12 moteurs, associe le nombre de moteurs en parfait état de marche de ce prélèvement.
-
La communication par courants porteurs en ligne (ou CPL) permet de transmettre des informations
en utilisant des conducteurs électriques en fonctionnement.
Le principe des CPL consiste à superposer au réseau électrique un signal de haute fréquence et de
basse énergie. Ce deuxième signal se propage sur l’installation électrique et peut être reçu et décodé
à distance.
Il est possible d'utiliser ce signal porteur pour transmettre des signaux numériques (bits) sur chaque période de ce signal porteur.
On admet que, dans certaines conditions des bits peuvent être mal transmis.
On transmet, durant chaque période, 80 bits. Chaque bit a une probabilité égale à 0,015 d’être mal
transmis.
On note $X$ la variable aléatoire qui associe à chaque période le nombre de bits mal transmis
durant cette période.
-
Quelle est la loi de probabilité suivie par la variable aléatoire $X$ ? Justifier rigoureusement et préciser les paramètres.
-
Calculer la probabilité que tous les bits soient correctement transmis durant une période.
Arrondir la réponse au millième. -
Calculer la probabilité que strictement plus de 4 bits soient mal transmis.
Arrondir la réponse au millième. -
-
Calculer l’espérance de la variable aléatoire $X$.
-
On considère que la ligne est de bonne qualité si, en moyenne, moins de deux bits sont mal transmis durant une période.
La ligne est-elle de bonne qualité?
-
Un grossiste en fournitures de bureau revend un ruban adhésif transparent répondant à deux critères :
-
pouvoir être repositionné au moins une fois sans arracher le support, noté $C1$ ;
-
ne pas jaunir le papier sur lequel il est posé, noté $C2$.
Les réponses des deux parties sont indépendantes. Les résultats numériques seront arrondis à $10^{-3}$.
Partie A :
Ce grossiste a trois fournisseurs AderOtop, ADZif et S.A.Col.
Il commande 27% des rubans adhésifs transparents chez AderOtop, 33 % chez ADZif et 40% chez S.A.Col.
Le pourcentage de rubans qui ne répondent pas au critère C1 est 2,9% chez AderOtop, 3,1% chez ADZif et
4,2% chez S.A.Col. Ensuite, les rubans sont répartis dans le rayon sans tenir compte du fournisseur.
-
Un client prend au hasard un ruban adhésif dans le rayon.
Montrez que la probabilité d’obtenir un ruban ne répondant pas au critère $C1$ est 0,035 à $10^{-3}$ près. -
Le chef de rayon, après réclamation d’un client, a en main un ruban adhésif ne répondant pas au critère $C1$. Quelle est la probabilité que ce ruban vienne de chez ADZif ?
Partie B :
La probabilité qu’un ruban adhésif jaunisse le papier est de 0,008.
Un client achète 500 rubans adhésifs. On assimilera le choix de ces 500 rubans à un tirage aléatoire avec remise.
On s’intéresse à la variable aléatoire $X$ qui compte, dans ce lot de 500 rubans adhésifs, le nombre de ceux
qui jaunissent le papier.
-
Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.
-
Quelle est la probabilité qu’au moins deux de ces 500 rubans adhésifs jaunisse le papier ?
Dans cet exercice, les résultats approchés sont, sauf mention du contraire, à arrondir à $10^{-3}$.
La vertéporfine est un médicament utilisé pour soigner une certaine forme de dégénérescence maculaire liée à
l’âge (D. M. L. A.).
Pour étudier l’efficacité de la vertéporfine pour soigner cette forme de D. M. L. A., une étude a été
réalisée auprès de 240 patients atteints de D. M. L. A. et âgés de plus de 50 ans.
Lors de cette étude, les patients ont été répartis en deux groupes constitués au hasard :
-
160 patients ont reçu un traitement à base de vertéporfine ;
-
80 patients ont reçu un placebo.
Après un an de traitement, les patients ont été examinés pour déterminer s’ils avaient perdu moins de
trois lignes d’acuité visuelle sur l’échelle E. T. D. R. S. par rapport à leur vision de départ.
Un tel patient est nommé « répondeur ».
Le tableau suivant indique pour chaque groupe le nombre de répondeurs.
| Groupe | Traitement à base de vertéporfine | Placebo |
|---|---|---|
| Nombre de répondeurs | 108 | 36 |
Partie A. Probabilités conditionnelles
On tire au hasard une fiche parmi celles des 240 patients concernés par l’étude.
On désigne par $V$ l’évènement « la fiche tirée est celle d’un patient ayant reçu le traitement à base de vertéporfine ».
On désigne par $R$ l’évènement « la fiche tirée est celle d’un répondeur ».
-
Construire un arbre de probabilités ou un tableau correspondant à la situation.
-
Calculer $P(R\cap V)$.
-
Montrer, par un calcul, que $P(R)=0,6$.
-
Sachant que la fiche tirée est celle d’un répondeur, quelle est la probabilité que ce patient ait reçu un traitement à base de vertéporfine ?
Partie B. Loi binomiale
Dans cette partie, on s’interroge sur la probabilité d’observer au moins 108 répondeurs sur un échantillon
aléatoire de taille 160 issu d’une population où la proportion des répondeurs est 0,6.
On tire au hasard et avec remise 160 fiches parmi celles des 240 patients concernés par l’étude. On suppose que la probabilité
qu’une fiche tirée soit celle d’un répondeur est $p=0,6$.
On désigne par $X$ la variable aléatoire qui, à tout prélèvement ainsi décrit, associe le nombre de fiches correspondant à
des répondeurs.
-
Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.
-
Calculer l’espérance de $X$ et en donner une interprétation.
-
Montrer, par un calcul, que $P(R)=0,6$.
-
-
Donner la probabilité qu’il y ait exactement 96 répondeurs parmi les 160 fiches prélevées.
-
Calculer $P(X>108)$.
-
Demander le programme !
-
Le vocabulaire sur les probabilités (issues, événement, univers, expérience aléatoire, ...)
-
La notion d'indépendance de deux événements.
-
Écrire une phrase concrète liée à l'aide d'événements.
-
Savoir utiliser un diagramme (de Venn) pour calculer des probabilités.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International