La transformée en $Z$ est très utile pour étudier les signaux numériques ainsi que des filtres numériques.

Série entière

Introduction

Voici ci-dessous une animation Geogebra qui permet de visualiser le comportement d'une succession particulière de polynômes vis-à-vis de la fonction exponentielle. Déplacer le curseur progressivement vers la droite pour visualiser le comportement de la suite de polynômes par rapport à la fonction exponentielle.

  1. Que pouvez-vous dire des polynômes par rapport à la fonction exponentielle au voisinage de $t=0$ ?

  2. Comment l'approximation évolue-t-elle en fonction du degré $n$ du polynôme considéré ?

  3. En généralisant l'approximation obtenue, on peut penser que la fonction exponentielle peut s'écrire sous la forme d'une somme infinie.
    Proposer une telle écriture.

L'écriture d'une fonction sous forme d'une somme infinie est appelée série entière.

Série géométrique

Le but est d'étudier la série $S(t)$ de terme général $u_n=t^n$, c'est-à-dire celle définie par $\displaystyle S(t)=\sum_{n=0}^{n=+\infty}t^n$.

  1. Démontrer que pour tout réel $t$ et tout entier naturel $m$, on a : $\displaystyle\left(\sum_{k=0}^{k=m}t^k\right)\times(1-t)=1-t^{m+1}$, c'est-à-dire que $\displaystyle\left(1+t+t^2+t^3+...+t^{m-1}+t^m\right)\times(1-t)=1-t^{m+1}$.

  2. En déduire que pour tout réel $t\neq 1$ et tout entier naturel $m$, on a : $\displaystyle\sum_{k=0}^{k=m}t^k=\dfrac{1-t^{m+1}}{1-t}$.

  3. Quelle est la limite de la suite $(t^n)$ lorsque $t$ tend vers $+\infty$ dans le cas où $-1<t<1$ ?

  4. En déduire que pour tout réel $t$ tel que $|t|<1$, on a : $\displaystyle\sum_{k=0}^{k=+\infty}t^k=\dfrac{1}{1-t}$.

  5. Voici ci-dessous une visualisation Geogebra qui permet de comparer suivant deux fenêtres différentes la fonction $t\mapsto \dfrac{1}{1-t}$ avec $t\mapsto \displaystyle\sum_{k=0}^{k=m}t^k$, pour différentes valeurs de $m$.

    1. Déplacer le curseur $m$, d'abord avec les flèches directionnelles, puis à la souris.

    2. Pour quelles valeurs de $t$, la série $\displaystyle\sum_{k=0}^{k=+\infty}t^k$ semble-t-elle exister ?

    3. Quelle fonction semble pouvoir s'écrire sous forme de la série $\displaystyle\sum_{k=0}^{k=+\infty}t^k$ au voisinage de 0 ?


La série $S(t)$ de terme général $u_n=t^n$, c'est-à-dire celle définie par $\displaystyle S(t)=\sum_{n=0}^{n=+\infty}t^n$, est appelée série géométrique.
Cette série est définie lorsque $|t|<1$ avec comme forme simplifiée : $\displaystyle S(t)=\sum_{n=0}^{n=+\infty}t^n=\dfrac{1}{1-t}$.
Dans ce cas, on parle de série convergente.

La série $\displaystyle S(t)=\sum_{n=0}^{n=+\infty}t^n$ est définie et existe sur l'intervalle $]-1;1[$.

Par contre, la fonction $t\mapsto \dfrac{1}{1-t}$ est définie sur $\mathbb{R}\setminus\{1\}$, c'est-à-dire pour tous les réels diférents de 1.

Définitions

On appelle série entière de la variable $t$ toute série de terme général $u_n=a_n t^n$, où $a_n$ est un réel et $n$ un nombre entier naturel.
Sur tout intervalle où la série est convergente, une série entière a pour somme une fonction $f$ : $f(t)=\displaystyle S(t)=\sum_{n=0}^{n=+\infty}a_n t^n$.

On peut généraliser cette définition avec la variable $z$ complexe avec $\displaystyle \sum_{n=0}^{n=+\infty}a_n z^n$.

On considère une série entière $\displaystyle \sum_{n=0}^{n=+\infty}a_n z^n$, avec $z\in \mathbb{R}$ ou $z\in \mathbb{C}$.

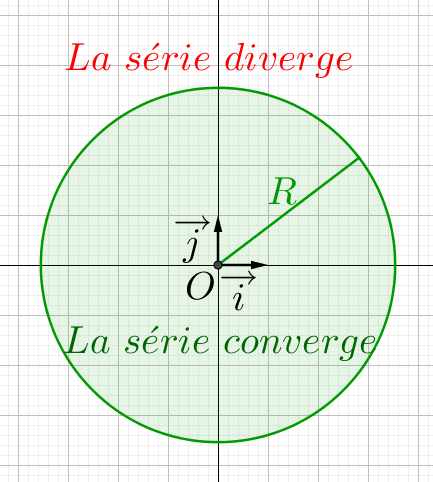
Le nombre $R$ est appelé, lorsqu'il existe, le rayon de convergence de la série.

Transformée en $Z$

Échantillonnage

En électronique, en électricité ou en mécanique, beaucoup de signaux sont analogiques c'est-à-dire correspondent à des fonctions définies sur $[0;+\infty[$ : le temps est alors une variable continue.

Connaître la fonction causale analogique revient à connaître toutes les images sur tout un intervalle voire sur $[0;+\infty[$ ; or, il y en a une infinité.

Il est donc nécessaire de discrétiser la fonction causale $f$ en ne prenant que des valeurs de $f$ espacées.

Les moyens actuels de traitement de l'information permettent de limiter les données concernant un signal à une liste de valeurs régulièrement prises par la fonction $f$. On parle alors de signal causal échantillonné. Ce type de signal est mathématiquement modélisé par une suite mathématique.

Plus précisément, on note $T_e$ la période fixée arbitrairement entre deux valeurs successives prises par $f$.
Le signal causal échantillonné correspond à la suite notée $(x(n))$ définie pour tout entier $n$ par $x(n)=f(nT_e)$.

On considère la fonction $\color{red}{causale}$ $f$ définie par $f(t)=6te^{-\frac{t}{2}}\color{red}{\mathcal{U}(t)}$.
Cette fonction est représentée ci-dessous.

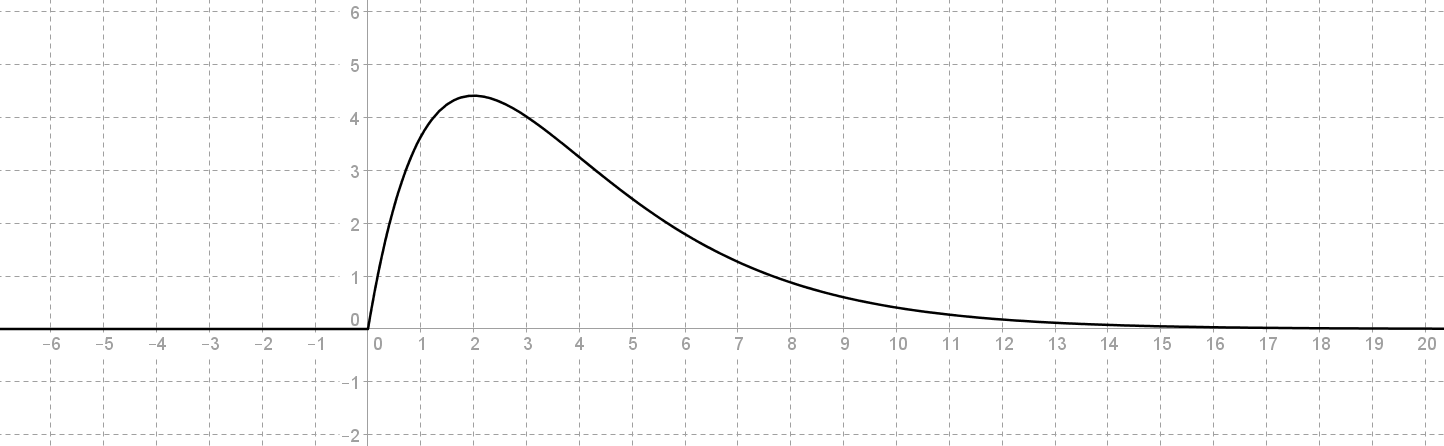
On décide d'échantillonner régulièrement avec une période $T_e$, ici $T_e=1.7$ :

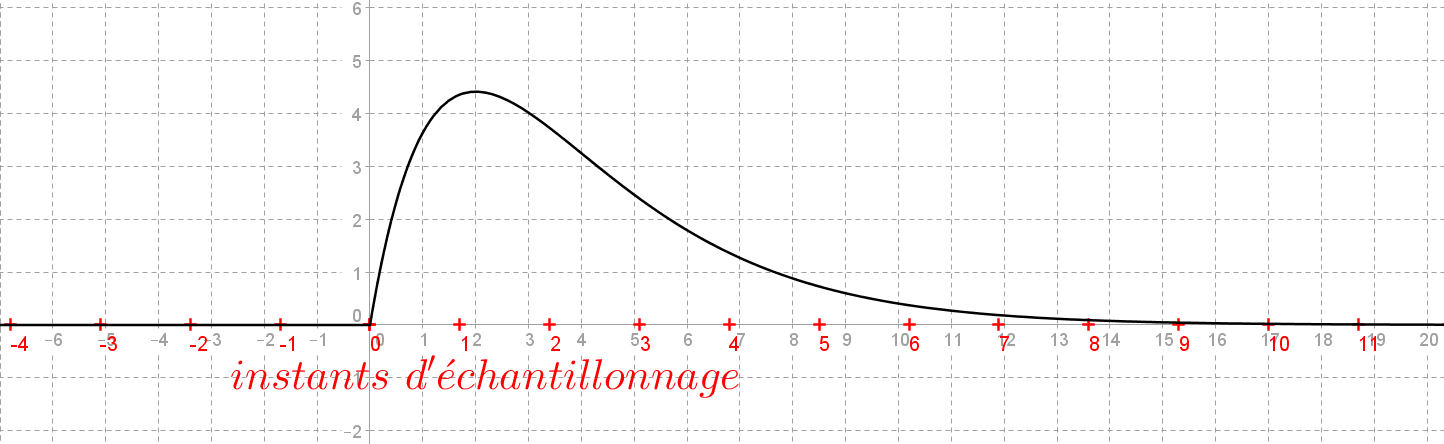
On mesure la valeur de $f$ à chacun des instants de l'échantillonnage :

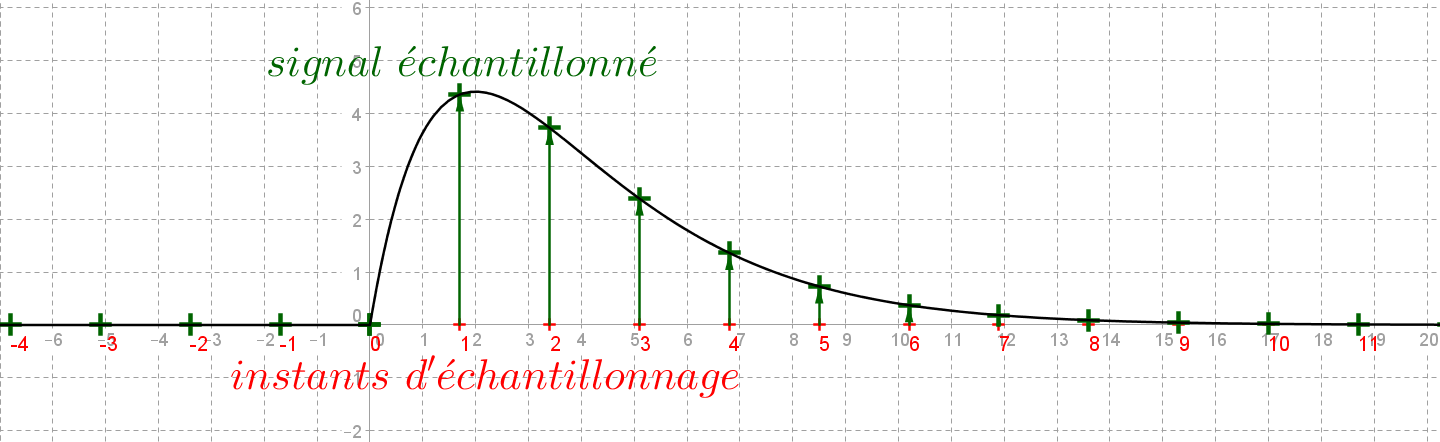
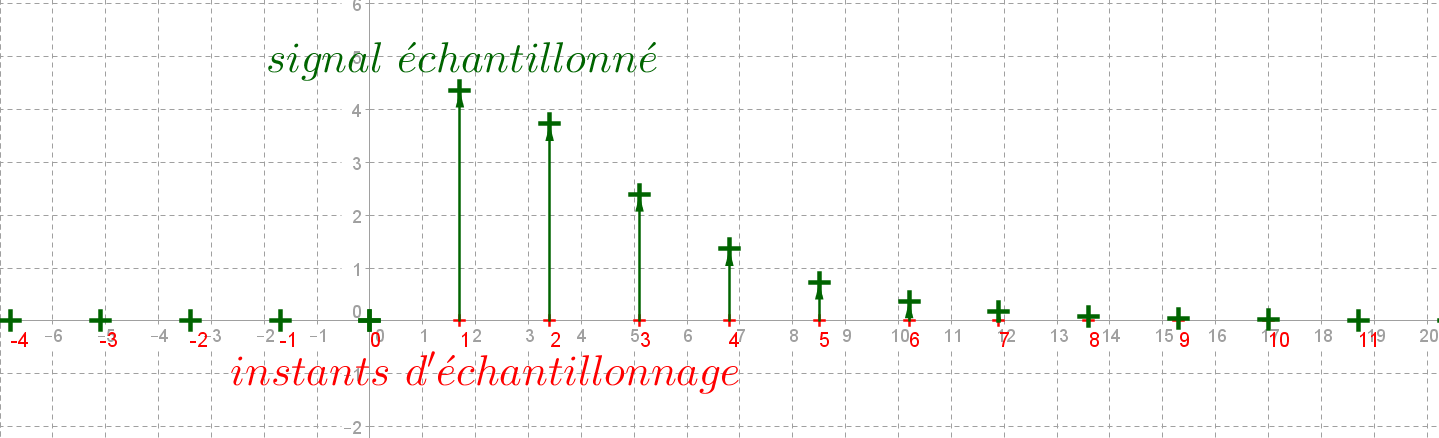
On obtient ainsi par échantillonnage le signal échantilloné, représenté par une suite de valeurs $\color{green}{x(n)=f(n T_e)}$ :

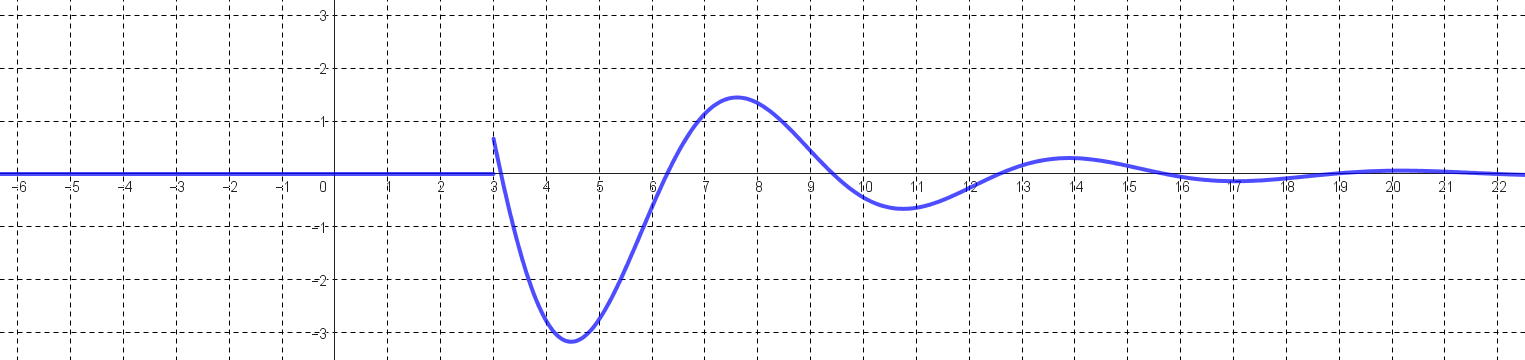
Voici ci-dessous la représentation graphique d'un signal analogique.

  1. Le signal analogique est-il causal ? Pourquoi ?

  2. Échantillonner le signal analogique avec une période $T_e=2$ pour obtenir le signal dicret échantillonné $(x(n))$.

  3. On admet que le signal analogique est donné par la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=0$ si $t<3$ et $f(t)=10 e^{-\frac{t}{4}} \sin(t)$ si $t\ge 3$.
    Quelle est l'expression de $x(n)$ en fonction de $n$.

Code de déblocage de la correction :

Définition de la transformée en $Z$

Maintenant que l'on sait obtenir un signal discret, voyons comme le transformer en une fonction pour l'étudier.

On considère $x:n\mapsto x(n)$ un signal causal discret.

La transformée en $Z$ du signal discret causal $x$ est la fonction $\displaystyle Zx:z\mapsto (Zx)(z)=\sum_{n=0}^{n=+\infty}x(n) z^{-n}$ définie pour tout $z$ tel que la série converge.
La variable $z$ est réelle ou complexe.

On peut écrire ainsi la transformée en $Z$ de $x$ : $\displaystyle Zx:z\mapsto (Zx)(z)=\sum_{n=0}^{n=+\infty}x(n) z^{-n}$ $\displaystyle =\sum_{n=0}^{n=+\infty}x(n) \left(\dfrac{1}{z}\right)^{n}$ $\displaystyle=x(0)+x(1)\times \dfrac{1}{z}+x(2)\times \dfrac{1}{z^2}+...+x(n)\times \dfrac{1}{z^n}+...$

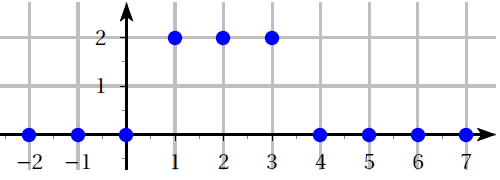
On considère le signal discret $x$ représenté ci-dessous.

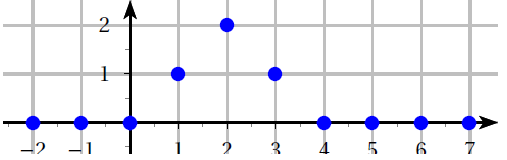
Le signal est bien causal car si $n<0$ alors $x(n)=0$.

Les seules valeurs non nulles du signal sont : $x(1)=1$, $x(2)=2$ et $x(3)=1$.

La transformée en $Z$ de ce signal est défini par : $(Zx)(z)=x(0)+x(1)\times \dfrac{1}{z}+x(2)\times \dfrac{1}{z^2}+...+x(n)\times \dfrac{1}{z^n}+...$ $=0+\dfrac{1}{z}+2\dfrac{1}{z^2}+\dfrac{1}{z^3}+0$ $=\dfrac{1}{z}+\dfrac{2}{z^2}+\dfrac{1}{z^3} \left(=\dfrac{z^2+2z+1}{z^3}\right)$.

À l’aide de la définition de la transformée en $Z$, donner l'expression des transformées en $Z$ des suites causales représentées graphiquement ci-dessous, sachant que pour chacune de ces suites $x(n)=0$ si $n\ge 4$ :

Transformée en $Z$ des suites de références

Pour les signaux non réduits à quelques valeurs, la simplification de l'écriture de la somme, qui peut contenir une infinité de termes, est possible grâce à des formules admises.
Il est essentiel de savoir passer d'un signal discret de référence à sa transformée en $Z$ par lecture de tableau, tableau qui synthétisera l'ensemble des formules qui vont être vues progressivement.

Impulsion de Dirac (impulsion unité discrète)

L'impulsion unité discrète (ou impulsion de Dirac) est le signal discret causal $d$ défini pour $n=0$ par $d(n)=1$ et si $n\neq 0$ par $d(n)=0$.
Voici la représentation graphique de cette impulsion unité discrète :

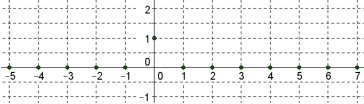
La transformée en $Z$ de l'impulsion unité discrète $d$ est $Zd:z\mapsto 1$.
Cette transformée en $Z$ est définie pour tout $z$ tel que $z\neq 0$.

  1. Sur Xcas, cette impulsion unité discrète peut être obtenue en saisissant : Kronecker(n).

  2. Pour obtenir la transformée en $Z$ d'une suite sur Xcas, il suffit de saisir : ztrans(terme général de la suite,n,z).

Dans ztrans(terme général de la suite,n,z), la variable de la suite doit être n et le troisième paramètre z permet d'obtenir comme affichage une fonction dont la variable est z.

Vérifier sur Xcas, l'expresssion de la transformée en $Z$ de l'impulsion de Dirac.

Échelon unité discret

L'échelon unité discret est le signal discret causal $e$ défini pour $n\ge 0$ par $e(n)=1$ et si $n\lt 0$ par $e(n)=0$.
Voici la représentation graphique de cet échelon unité discret :

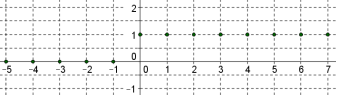
La transformée en $Z$ de l'échelon unité discret $e$ est $Ze:z\mapsto \dfrac{z}{z-1}$.
Cette transformée en $Z$ est définie pour tout $z$ tel que $|z|\lt 1$.

Sur Xcas, cet échelon unité discret peut être obtenue en saisissant : Heaviside(n).

Retrouver sur Xcas, l'expression de la transformée en $Z$ de l'échelon unité discret.

Rampe causale discrète

La rampe causale discrète est le signal discret causal $r$ défini pour $n\ge 0$ par $r(n)=n$ et si $n\lt 0$ par $r(n)=0$.
Voici la représentation graphique de cette rampe causale discrète :

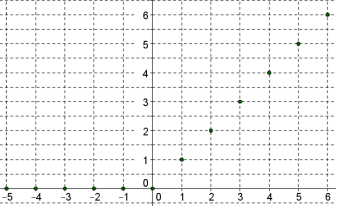
Pour obtenir la rampe causale discrète sur Xas, il suffit de saisir n*Heaviside(n).

Trouver sur Xcas, l'expression factorisée de la transformée en $Z$ de la rampe causale discrète.

La transformée en $Z$ de la rampe causale discrète $r$ est $Zr:z\mapsto \dfrac{z}{(z-1)^2}$.
Cette transformée en $Z$ est définie pour tout $z$ tel que $|z|\lt 1$.

Signal causal carré discret

Le signal causal carré discret est le signal discret causal $c$ défini pour $n\ge 0$ par $c(n)=n^2$ et si $n\lt 0$ par $c(n)=0$.
Voici la représentation graphique de ce signal causal carré discret :

Pour obtenir le signal causal carré discret sur Xas, il suffit de saisir n^2*Heaviside(n).

Trouver sur Xcas, l'expression factorisée de la transformée en $Z$ du signal causal carré discret.

La transformée en $Z$ du signal causal carré discret $c$ est $Zc:z\mapsto \dfrac{z(z+1)}{(z-1)^3}$.
Cette transformée en $Z$ est définie pour tout $z$ tel que $|z|\lt 1$.

Signal causal exponentiel discret

Le signal causal exponentiel discret est le signal discret causal $f$ défini pour $n\ge 0$ par $f(n)=a^n$, où $a$ est un réel non nul fixé, et si $n\lt 0$ par $f(n)=0$.
Voici la représentation graphique de ce signal causal exponentiel discret dans le cas où $a=2$ :

Pour obtenir le signal causal exponentiel discret sur Xas, il suffit de saisir a^n*Heaviside(n).

Trouver sur Xcas, l'expression factorisée de la transformée en $Z$ du signal causal exponentiel discret.

La transformée en $Z$ du signal causal carré discret $f$ est $Zf:z\mapsto \dfrac{z}{z-a}$.
Cette transformée en $Z$ est définie pour tout $z$ tel que $|z|\lt |a|$.

Propriétés de la transformée en $Z$

Linéarité

Soient $f$ et $g$ deux signaux causaux admettant des transformées en $Z$ et $\alpha$ et $\beta$ deux nombres réels.
On a : $(Z(\alpha f+\beta g))=\alpha (Zf)+\beta Z(g)$.

  1. Rapeller la transformée en $Z$ du signal causal défini sur $\mathbb{N}$ par $s(n)=n$.

  2. En utilisant la propriété de linéarité en remarquant que $3=3\times 1$, déterminer la transformée en $Z$ du signal causal défini sur $\mathbb{N}$ par $t(n)=3$.

  3. En utilisant la propriété de linéarité, en déduire la transformée en $Z$ du signal causal défini sur $\mathbb{N}$ par $u(n)=2n+3$.

  4. Utiliser Xcas pour vérifier l'expression de la transformée en $Z$ trouvée pour le signal $u$ précédent.

    Penser à mettre l'expression obtenue à la main et celle sur Xcas sous la même forme pour pouvoir facilement les comparer.

Multiplication par $a^n$

Soit $x$ un signal causal admettant une transformée en $Z$ et soit $y$ le signal causal défini sur $\mathbb{N}$ par $y(n)=a^n\times x(n)$.
$y$ admet alors une transformée en $Z$.
De plus, les transformées en $Z$ des signaux $x$ et $y$ sont liées par la relation : $(Zy)(z)=(Zx)\left(\dfrac{z}{a}\right)$.
Cette formule signifie qu'en pratique :

  1. On commence par trouver la transformée en $Z$ du signal $x$ (sans le facteur $a^n$),

  2. On remplace dans l'expression de cette transformée en $Z$ tous les $z$ par la fraction $\dfrac{z}{a}$.

On considère le signal $y(n)=n^2\times 5^n$.

Pour obtenir la transformée en $Z$ de ce signal, on remarque que $y(n)$ peut être vu comme $x(n)\times a^n$ avec $x(n)=n^2$ et $a^n=5^n$. Ainsi, on procède en deux étapes :

  1. Étape 1 : transformée en $Z$ du signal sans le facteur $a^n$ :
    $y(n)=n^2\times 5^n$. On cherche la transformée en $Z$ de $n^2$.
    La tranformée en $Z$ de $n^3$ est $\dfrac{z(z+1)}{(z-1)^3}$.

  2. Étape 2 : remplacer $z$ par $\dfrac{z}{a}$ :
    Ici $a=5$ puisque $y(n)=n^2\times 5^n$.
    Ainsi, $Zy(z)=\dfrac{\color{red}{\dfrac{z}{5}}\left(\color{red}{\dfrac{z}{5}}+1\right)}{\left(\color{red}{\dfrac{z}{5}}-1\right)^3}$.
    Si on veut modifier la forme de cette transformée, il suffit d'utiliser Xcas.

Le but est d'obtenir à la main puis sur Xcas la transformée en $Z$ du signal causal défini sur $\mathbb{N}$ par $s(n)=4n\times 3^n$.

  1. Quelle forme globale voyez-vous apparaître dans l'expression de $s(n)$ ?

  2. Déterminer à la main l'expression de la transformée en $Z$ du signal causal défini sur $\mathbb{N}$ par $t(n)=4n$.

  3. En déduire en utilisant le théoème précédent, l'expression de la transformée en $Z$ du signal causal $s$.

  4. Vérifier sur Xcas, l'expression obtenue de la transformée en $Z$ du signal causal $s$.

Translation sur la variable $z$ : cas du retard

Soit $x$ un signal discret.
Notons $e$ la fonction échelon unité discret.
Le signal $n\mapsto x(n-n_0)e(n-n_0)$ est le signal retardé de $n_0$.

Voici la représentation d'un signal causal $x$ :

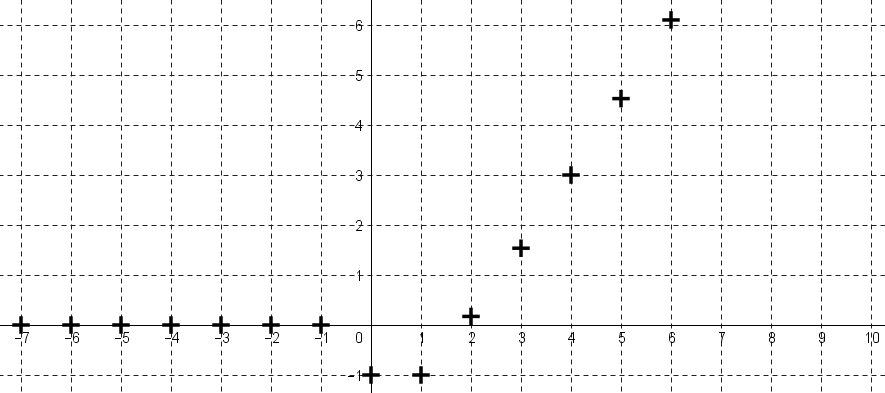
Voici la représentation avec des croix rouge du signal retardé de 3 :

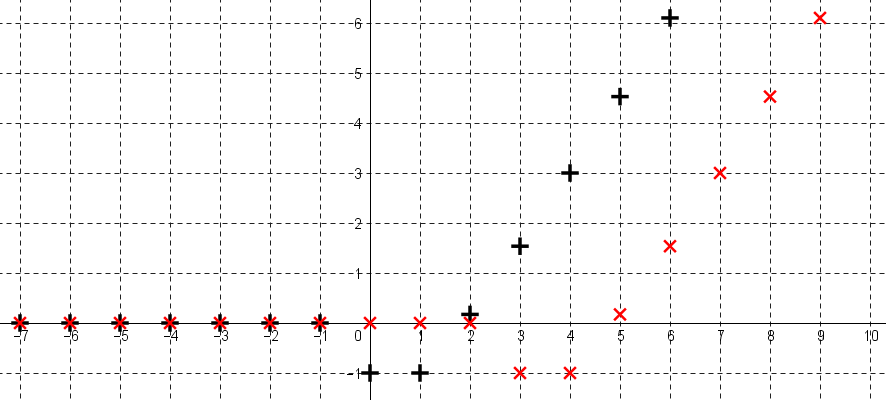
Notons $y$ le signal $x$ retardé de 3.
Le signal $y$ est défini sur $\mathbb{N}$ par $\color{red}{y:n\mapsto x(n-3) e(n-3)}$, où $e$ est l'échelon unité discret.

On note $x(n)$ la suite causale tracée ci-contre :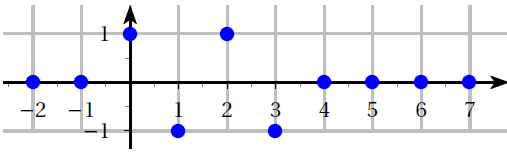

  1. Reproduire le signal $x$ puis tracer le signal retardé de 2, signal noté $y$.

  2. Déterminer l'expression du signal rétardé $y$ en fonction du signal $x$.

  3. Déterminer, à l'aide du graphique obtenu, la transformée en $Z$ du signal $y$, transformée écrite $(Zy)$.

  4. On rappelle que l'on a déjà démontré que le signal $x$ admet comme transformée en $Z$ : $(Zx)(z)=1-\dfrac{1}{z}+\dfrac{1}{z^2}-\dfrac{1}{z^3}$.
    Quel lien pouvez-vous deviner entre $(Zx)$ et $(Zy)$ ?

Soient $x$ un signal discret causal admettant une transformée en $Z$ et soit $y$ le signal $x$ retardé de $n_0$.

Le signal $y$ admet une transformée en $Z$, notée $(Zy)$, défini par $(Zy)(z)=z^{-n_0}\times (Zx)(z)$.

Le coefficient multiplicateur $z^{-n_0}$ apparaissant dans l'expression de la transformée en $Z$ du signal retardé est appelé facteur retard.

Soit $s$ le signal causal défini sur $\mathbb{N}$ par $s(n)=\dfrac{n^2}{2}$ . Soit $f$ le signal causal $s$ retardé de 2.

  1. Réprésenter sur une feuille quadrillée la représentation graphique du signal $s$.

  2. En déduire la représentation graphique du signal $f$.

  3. Déterminer à la main l'expression de la transformée en $Z$ du signal causal $s$.

  4. En déduire l'expression de la transformée en $Z$ du signal $f$.

  5. Retrouver sur Xcas l'expression de la transformée en $Z$ des signaux causaux $s$ et $f$.

Translation sur la variable z : cas de l'avance

Soit $x$ est un signal discret.
Notons $e$ l'échelon unité discret.
$f:n\mapsto x(n+n_0)e(n+n_0)$ est le signal avancé de $n_0$.

Voici la représentation graphique d'un signal causal $x$ :

Le signal avancé de 3 est représenté par les croix rouge suivantes :

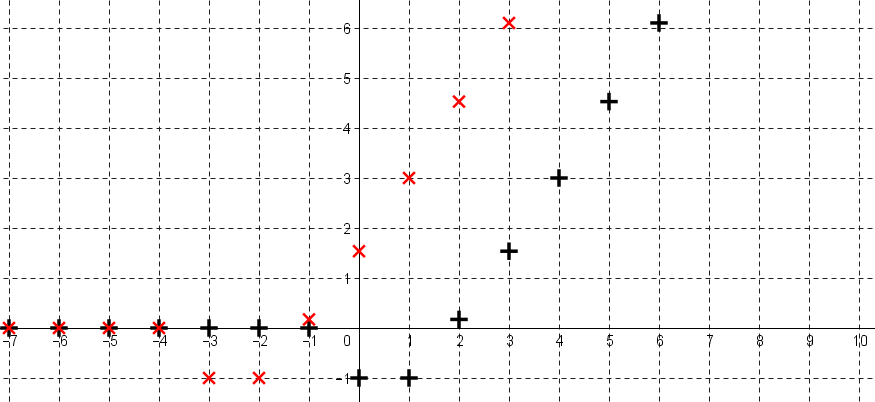
En notant $y$ le signal avancé de 3, $y$ est défini, pour tout entier relatif $n$, par $\color{red}{y(n)=x(n+3) e(n+3)}$.

Comme le prouve l'exemple précédent un signal avancé d'un signal causal n'est pas forcément causal.
Un signal $y$ avancé de $n_0$ d'un signal causal $x$ est aussi un signal causal si, et seulement si, $x(0)=x(1)=...=x(n_0-1)=0$.

Soit $x$ est un signal discret.
Notons $e$ l'échelon unité discret.
$f:n\mapsto x(n+n_0) e(\underline{n})$ est le signal causal avancé de $n_0$.

Voici la représentation graphique d'un signal causal $x$ :

Le signal causal avancé de 3 est représenté par les ronds vert suivants :

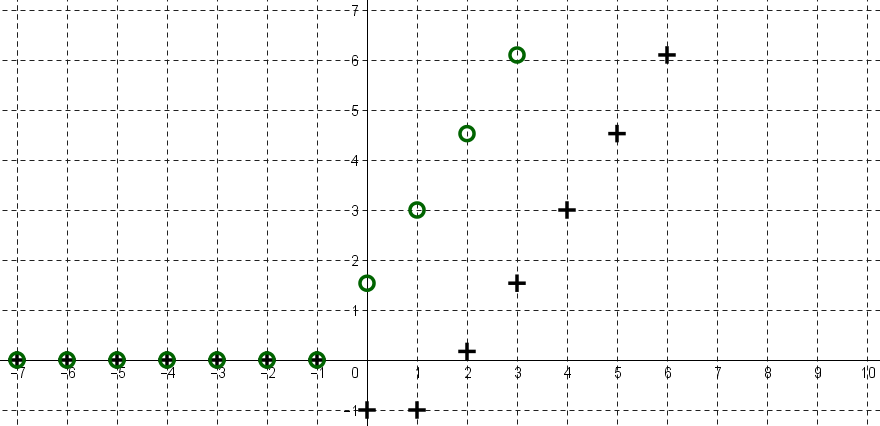
En notant $y$ le signal avancé de 3, $y$ est défini, pour tout entier relatif $n$, par $\color{red}{y(n)=x(n+3) e(n)}$.

  1. Pour passer d'un signal causal à un signal (pas forcément causal) avancé de $n_0$ on décale les termes de $n_0$ rangs.

  2. Pour passer d'un signal (pas forcément causal) avancé de $n_0$ à un signal causal avancé de $n_0$, il suffit d'annuler les $n_0$ premiers termes du signal avancé discret.

On note $x(n)$ la suite causale tracée ci-contre :

  1. Reproduire le signal $x$ puis tracer le signal retardé de 1, signal noté $y$.

  2. Déterminer l'expression du signal rétardé $y$ en fonction du signal $x$.

  3. Ce signal $y$ est-il causal ?

  4. Tracer le signal causal avancé de $1$, signal noté $w$.

  5. Déterminer l'expression du signal causal $w$ en fonction du signal $x$.

  6. Déterminer, à l'aide du graphique obtenu, la transformée en $Z$ du signal $w$, transformée écrite $(Zw)$.

  7. On rappelle que l'on a déjà démontré que le signal $x$ admet comme transformée en $Z$ : $(Zx)(z)=1-\dfrac{1}{z}+\dfrac{1}{z^2}-\dfrac{1}{z^3}$.
    Quel lien pouvez-vous deviner entre $(Zx)$ et $(Zw)$ ?

Soit $x$ un signal discret causal admettant une transformée en $Z$ notée $(Zx)$.
Soit $y$ le signal causal $x$ avancé de 1.
Le signal $y$ admet une transformée en $Z$ notée $(Zy)$ et cette transformée est définie par : $(Zy)(z)=z[(Zx)(z)-x(0)]$.

On peut retenir cette formule en y retrouvant les deux idées trouvées graphiquement pour obtenir la représentation graphique d'un signal causal avancé :

On considère le signal causal $x$ défini par la représentation graphique suivante :
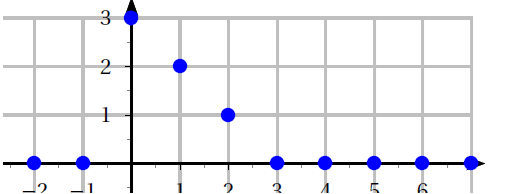
On avait montré dans un exercice précédent que la transformée en $Z$ de ce signal est donné par $(Zx)(z)=3+\dfrac{2}{z}+\dfrac{1}{z^2}$.

On considère le signal $y$ qui est le signal causal $x$ avancé de 1.

  1. Déterminer une expression de la transformée en $Z$ du signal $y$.

  2. Représenter graphiquement le signal $y$.

  3. Vérifier graphiquement l'expression de la transformée en $Z$ du signal $y$ trouvée.

On considère le signal causal $x$ défini sur $\mathbb{N}$ par $x(n)=(2^n-5)e(n)$, où $e$ est l'échelon unité discret.
Soit $y$ le signal causal $x$ avancé de 1.

  1. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  2. Vérifier sur Xcas l'expression de la transformée en $Z$ de $x$ trouvée.

  3. En déduire l'expression de la transformée en $Z$ de $y$.

  4. Exprimer $y(n)$ en fonction de $x(n)$.

  5. Vérifier sur Xcas l'expression de la transformée en $Z$ de $y$ trouvée.

Soit $x$ un signal discret causal admettant une transformée en $Z$ notée $(Zx)$.
Soit $y$ le signal causal $x$ avancé de 2.
Le signal $y$ admet une transformée en $Z$ notée $(Zy)$ et cette transformée est définie par : $(Zy)(z)=z^2[(Zx)(z)-x(0)-x(1)\times z^{-1}]$.

Là encore, on peut retenir cette formule en y retrouvant les deux idées trouvées graphiquement pour obtenir la représentation graphique d'un signal causal avancé :

On considère le signal causal $x$ défini par la représentation graphique suivante :
On avait montré dans un exercice précédent que la transformée en $Z$ de ce signal est donné par $(Zx)(z)=\dfrac{1}{z}+\dfrac{2}{z^2}+\dfrac{1}{z^3}$.

On considère le signal $y$ qui est le signal causal $x$ avancé de 2.

  1. Déterminer une expression de la transformée en $Z$ du signal $y$.

  2. Représenter graphiquement le signal $y$.

  3. Vérifier graphiquement l'expression de la transformée en $Z$ du signal $y$ trouvée.

On considère le signal causal $x$ défini sur $\mathbb{N}$ par $x(n)=(2n^2-3n+4)e(n)$, où $e$ est l'échelon unité discret.
Soit $y$ le signal causal $x$ avancé de 2.

  1. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  2. Vérifier sur Xcas l'expression de la transformée en $Z$ de $x$ trouvée.

  3. En déduire l'expression de la transformée en $Z$ de $y$.

  4. Exprimer $y(n)$ en fonction de $x(n)$.

  5. Vérifier sur Xcas l'expression de la transformée en $Z$ de $y$ trouvée.

On peut généraliser la formule de l'avance :

Soit $x$ un signal discret causal admettant une transformée en $Z$ notée $(Zx)$.
Soit $y$ le signal causal $x$ avancé de $n_0$.
Le signal $y$ admet une transformée en $Z$ notée $(Zy)$ et cette transformée est définie par : $(Zy)(z)=z^{n_0}[(Zx)(z)-x(0)-x(1)\times z^{-1}-...-x(n_0)\times z^{-n_0}]$.

Là encore, on peut retenir cette formule en y retrouvant les deux idées trouvées graphiquement pour obtenir la représentation graphique d'un signal causal avancé :

On considère le signal causal $x$ défini sur $\mathbb{N}$ par $x(n)=\dfrac{n}{3}e(n)$, où $e$ est l'échelon unité discret.
Soit $y$ le signal causal $x$ avancé de 4.
Voici une représentation graphique du signal $x$ :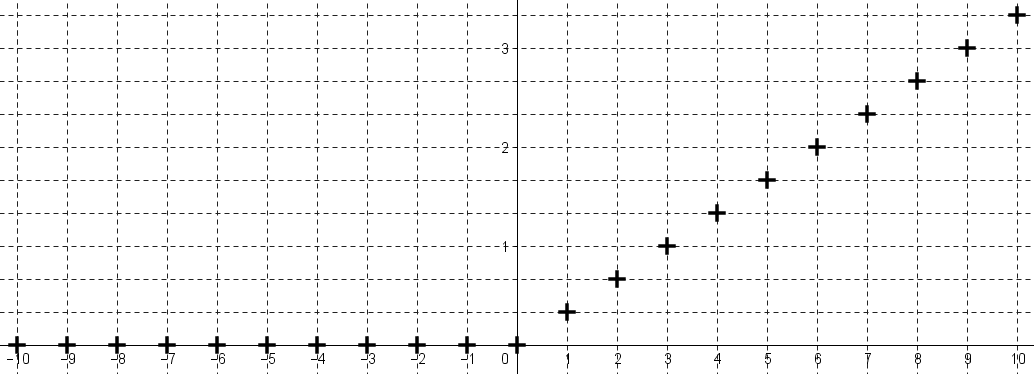

  1. Reproduire la représentation graphique du signal $x$ puis tracer la représentation graphique du signal $y$.

  2. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  3. Vérifier sur Xcas l'expression de la transformée en $Z$ de $x$ trouvée.

  4. En déduire l'expression de la transformée en $Z$ de $y$.

  5. Exprimer $y(n)$ en fonction de $x(n)$.

  6. Vérifier sur Xcas l'expression de la transformée en $Z$ de $y$ trouvée.

Deux théorèmes utiles en physique

Les deux formules suivantes sont utiles en physiques pour prendre en compte les conditions initiales et pour étudier la tendance à long terme d'un phénomène.

Théorème de la valeur initiale :

Soit $x$ un signal causal discret. Si cette limite existe, on a : $\displaystyle \lim_{z\to +\infty}(Zx)(z)=x(0)$.

Théorème de la valeur finale :

Soit $x$ un signal causal discret. Si ces limites existent, on a : $\displaystyle \lim_{z\to 1}(z-1)\times (Zx)(z)=\lim_{n \to +\infty}x(n)$.

Voici un tableau résumant les transformées en $Z$ usuelles et les propriétés essentielles :

Signal causal discret

Transformée en $Z$

$e(n)=1$ si $n\ge 0$ et $e(n)=0$ si $n\lt 0$.

$(Ze)(z)=\dfrac{z}{z-1}$

$d(n)=1$ si $n=0$ et $d(n)=0$ si $n\neq0$.

$(Zd)(z)=1$

$r(n)=n$ si $n\ge 0$ et $r(n)=0$ si $n\lt 0$.

$(Zr)(z)=\dfrac{z}{(z-1)^2}$

$c(n)=n^2$ si $n\ge 0$ et $c(n)=0$ si $n\lt 0$.

$(Zc)(z)=\dfrac{z(z+1)}{(z-1)^3}$

$p(n)=a^n$ si $n\ge 0$, avec $a\neq 0$, et $p(n)=0$ si $n\lt 0$.

$(Zp)(z)=\dfrac{z}{z-a}$

$y(n)=x(n)\times a^n$, avec $a\neq 0$.

$(Zy)(z)=(Zx)\left(\dfrac{z}{a}\right)$

$y(n)=x(n-n_0)e(n-n_0)$.

$(Zy)(z)=z^{-n_0}\times (Zx)(z)$

$y(n)=x(n+1)e(n)$.

$(Zy)(z)=z[(Zx)(z)-x(0)]$

$y(n)=x(n+2)e(n)$.

$(Zy)(z)=z^2[(Zx)(z)-x(0)-x(1)z^{-1}]$

$y(n)=x(n+n_0)e(n)$.

$(Zy)(z)=z^{n_0}[(Zx)(z)-x(0)-x(1)z^{-1}-...-x(n_0)z^{-n_0}]$

Exercices

Liens avec un graphique

On considère le signal causal $x$ défini par la représentation graphique suivante :
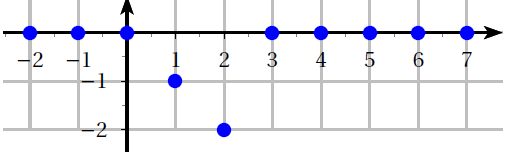
On avait montré dans un exercice précédent que la transformée en $Z$ de ce signal est donné par $(Zx)(z)=-\dfrac{1}{z}-\dfrac{2}{z^2}$.

On considère le signal $y$ qui est le signal causal $x$ retardé de 2.

  1. Déterminer à la main une expression de la transformée en $Z$ du signal $y$.

  2. Représenter graphiquement le signal $y$.

  3. Vérifier graphiquement l'expression de la transformée en $Z$ du signal $y$ trouvée.

On considère le signal causal $x$ défini par $x(n)=2$ si $0\le n\le 4$ et $x(n)=0$ si $n\lt 0$ ou si $n\gt 4$.

On considère le signal $y$ qui est le signal causal $x$ retardé de 1.

  1. Représenter graphiquement le signal $x$.

  2. En s'aidant du graphique, déterminer la transformée en $Z$ du signal causal $x$.

  3. Déterminer à la main une expression de la transformée en $Z$ du signal $y$.

  4. Représenter graphiquement le signal $y$.

  5. Vérifier graphiquement l'expression de la transformée en $Z$ du signal $y$ trouvée.

On considère le signal causal $x$ défini par la représentation graphique suivante :
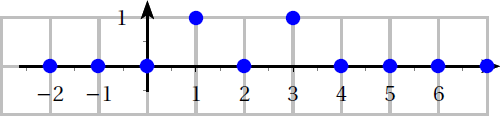
On avait montré dans un exercice précédent que la transformée en $Z$ de ce signal est donné par $(Zx)(z)=\dfrac{1}{z}+\dfrac{1}{z^3}$.

On considère le signal $y$ qui est le signal causal $x$ avancé de 2.

  1. Déterminer à la main une expression de la transformée en $Z$ du signal $y$.

  2. Représenter graphiquement le signal $y$.

  3. Vérifier graphiquement l'expression de la transformée en $Z$ du signal $y$ trouvée.

Utilisation du tableau de formules

Déterminer, à la main puis sur Xcas, la fonction qui est la transformée en $Z$ de la suite causale donnée dans chacun des cas, sachant que $e$ est l'échelon unité discret défini par $e(n)=1$ si $n\ge 0$ et $e(n)=0$ sinon.

  1. $x(n)=\left(2n^2-n+4\right)e(n)$

  2. $x(n)=n\left(-1\right)^n e(n)$

  3. $x(n)=(n-4)e(n-4)$

  4. $x(n)=(n+2)^2 e(n)$

  5. $x(n)=\left(2^n-\dfrac{n^2}{4}+1\right)e(n)$

  6. $x(n)= (n-2)^2 e(n-2)$

  7. $x(n)= 4 d(n)$, où $d(n)=1$ si $n=0$ et $d(n)=0$ sinon.

  8. $x(n)=3^{n-1} e(n)$

  9. $x(n)=n^2\times 2^{n} e(n)$

  10. $x(n)=4\times (-1)^n e(n)$

Déterminer, à la main puis sur Xcas, la fonction qui est la transformée en $Z$ de la suite causale donnée dans chacun des cas, sachant que $e$ est l'échelon unité discret défini par $e(n)=1$ si $n\ge 0$ et $e(n)=0$ sinon.

  1. $x(n)=(n+1)^2e(n-1)$

  2. $x(n)=\left(n^2\times 3^n\right) e(n)$

  3. $x(n)=n\times d(n)$ où $d(n)=1$ si $n=0$, $d(n)=0$ sinon.

  4. $x(n)=(n-3)\times e(n-3)$

  5. $x(n)=3^ne(n)$

  6. $x(n)= \left(\dfrac{4}{3} \times (-1)^{n-1}- \dfrac{1}{3} \times 2^{n-1}\right)e(n-1)$

  7. $x(n)= \left(\dfrac{1}{3}\right)^n e(n)$

  8. $x(n)= \left(\dfrac{1}{2}\right)^{n-2}\times \left(\dfrac{1}{3}\right)^{n} e(n)$

  9. $x(n)=\left(\dfrac{1}{2}n^2+ \dfrac{1}{2} n+1\right) e(n)$

  10. $x(n)= \left(\dfrac{4n-3}{2^n}\right) e(n)$

Soit $x$ le signal causal défini sur $\mathbb{N}$ par $x(n)=2-n+\left(\dfrac{1}{2}\right)^n$.

Soit $y$ le signal causal $x$ retardé de 2.

  1. Exprimer $y(n)$ en fonction de $x(n)$.

  2. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  3. En déduire l'expression de la transformée en $Z$ de $y$.

  4. Retrouver les deux transformées précédentes en utilisant Xcas.

Soit $x$ le signal causal défini sur $\mathbb{N}$ par $x(n)=2-\left(-\dfrac{1}{3}\right)^n$.

Soit $y$ le signal causal $x$ avancé de 1.

  1. Exprimer $y(n)$ en fonction de $x(n)$.

  2. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  3. En déduire l'expression de la transformée en $Z$ de $y$.

  4. Retrouver les deux transformées précédentes en utilisant Xcas.

Soit $x$ le signal causal défini par $x(n)=\left( 4n-3 \right) e(n)$.

Soit $y$ le signal causal $x$ avancé de 2.

  1. Exprimer $y(n)$ en fonction de $x(n)$.

  2. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  3. En déduire l'expression de la transformée en $Z$ de $y$.

  4. Retrouver les deux transformées précédentes en utilisant Xcas.

Soit $x$ le signal causal défini par $x(n)=\left(3n^2-2n+6\right)e(n)$.

Soit $y$ le signal causal $x$ retardé de 2.

  1. Exprimer $y(n)$ en fonction de $x(n)$.

  2. Déterminer à la main l'expression de la transformée en $Z$ de $x$.

  3. En déduire l'expression de la transformée en $Z$ de $y$.

  4. Retrouver les deux transformées précédentes en utilisant Xcas.

Lien avec des suites particulières

On considère l'équation aux différences suivantes $y(n+1)=2y(n)$, si $n\ge 0$, avec $y(0)=1$.

  1. Calculer les valeurs de $y(1)$, $y(2)$, $y(3)$ et $y(4)$.

  2. Déterminer la nature de la suite $(y(n))$.

  3. Déterminer la transformée en $Z$ de la suite $(y(n)e(n))$.

  4. Utiliser le théorème de la valeur finale pour vérifier la limite de $y(n)$ lorsque $n$ tend vers $+\infty$.

Échantillonnage et équation différentielle

On dispose d'un filtre analogique passe bas du premier ordre dont l'équation différentielle est $7s'(t)+s(t)=f(t)$, où $s$ est la fonction causale associée au signal analogique de sortie, $f$ est la fonction causale associée au signal analogique d'entrée et où le coefficient 7 correspond à la valeur 7 ms de la constante de temps $\tau$ du filtre analogique, l'unité pour le temps $t$ étant la milliseconde.

On peut alors réaliser un filtre numérique passe-bas du premier ordre tel que :

  1. Montrer que l'équation aux différences peut s'écrire $y(n)= \dfrac{7}{8} y(n-1)+ \dfrac{1}{8} x(n)$.

  2. Dans cette question, on suppose que le signal d'entrée $x$ est l'impulsion unité discrète $d$ définie par $d(0)=1$ et par $d(n)=0$ si $n\neq 0$.

    1. Calculer $y(0)$ sachant que la suite $y$ correspond à un signal causal.

    2. Calculer successivement $y(n)$ pour les valeurs de $n$ comprises entre 1 et 3.

    3. À partir des valeurs trouvées, proposer, sans démonstration, une expression de $y(n)$ en fonction de $n$.

    4. Vérifier votre expression conjecturée en calculant $y(4)$.

    5. Déterminer l'expression de la transformée en $Z$ du signal $y$.

    6. Déterminer de deux manières la limite suivante : $\displaystyle \lim_{n\to +\infty} y(n)$.

La vitesse de rotation est régulée numériquement. Le cadencement de calcul se fait à une fréquence, notée $f_e$, de 20 khz. Le système, constitué par l’ensemble moteur alimenté par l’onduleur, fonctionne en boucle fermée avec un correcteur numérique. Ce système peut être identifié à un deuxième ordre numérique.
L’ensemble est schématisé sur la figure ci-dessous, $s_n$ désignant la vitesse (en tr/min) à l’instant $nT_e$, $e_n$ désignant la consigne (=l'entrée) (en tr/min) à l’instant $nT_e$. $T_e$ est la période de calcul donnée par $T_e= \dfrac{1}{f_e}$.

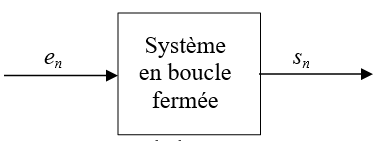
L’équation récurrente caractéristique du système en boucle fermée est : $s_n=\dfrac{1}{6} s_{n-1}+ \dfrac{2}{6} s_{n-2}+ \dfrac{1}{6} e_{n}$.
Le système étant au repos ($s_n$ et en nulles pour $n\lt 0$), on souhaite étudier la réponse à un échelon.
La consigne en vitesse en passe donc de 0 à 100 tr/min à $n=0$.

  1. Reproduire et compléter le tableau suivant en indiquant les 6 première valeurs de $t=nT_e$ et de $s_n$.

    $n$ $n\lt 0$ 0 1 2 3 4 5
    $t=nT_e$ (en $\mu$s) $t\lt 0$
    $e_n$ 0 150 150 150 150 150 150
    $s_n$ 0

  2. Quelle est la valeur en régime permanent de $s_n$, c'est-à-dire la valeur $s_{perm}$ telle que losque $t$ tend vers $+\infty$ $s_n\approx s_{n+1}\approx s_{n+2}\approx ...\approx s_{perm}$ ?

  3. Parmi les propositions suivantes, une correspond à l'expression de $s_n$ en fonction de $n$, si $n\ge 0$. Laquelle ?

    • $s_n=\dfrac{25 \left(\dfrac{1}{2}\right)^n -200 \left(\dfrac{3}{2}\right)^n + 350}{7}$

    • $s_n=\dfrac{25 \left(\dfrac{1}{2}\right)^n -200 \left(\dfrac{2}{3}\right)^n + 350}{7}$

    • $s_n=\dfrac{25 \left(-\dfrac{1}{2}\right)^n -200 \left(\dfrac{2}{3}\right)^n + 350}{7}$

  4. Déterminer la transformée en $Z$ de $s_n$.

  5. Déterminer de deux façons différentes la limite $\displaystyle \lim_{n\to +\infty}s_n$. Quelle interprétation concrète en donner ?

On considère un filtre dont le schéma est donné ci-contre : $s$ représente la tension entre les bornes du condensateur lorsque le circuit est alimenté par une source de tension $v$ et parcouru par un courant $i$.

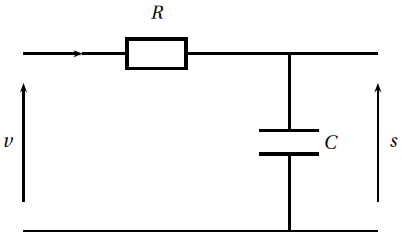
Les fonctions $s$ et $v$ sont liées par l’équation différentielle suivante : $RCs'(t)+s(t)=v(t)$ (1).

De plus, on suppose que $s(t)=0$, pour tout nombre réel $t$ négatif ou nul.
Pour tout l’exercice on considère que $R=250.103\ \Omega$ et $C=20.10^{-9}\ F$.

Partie A : signal analogique :

On considère que la tension $v$ est constante à $3\ V$.

  1. Montrer que l’équation différentielle (1) s’écrit alors : $0.005s'(t)+s(t)=v(t)$.

  2. Déterminer, à l'aide de Xcas, la solution $s$ l'équation différentielle $0.005s'(t)+s(t)=3$, sachant que $s(0)=0$.

Partie B : échantillonnage :

On peut discrétiser ce filtre analogique en un filtre numérique du premier ordre tel que : $0.005s'(t)+s(t)=v(t)$.

  1. Montrer que l'équation aux différences peut s'écrire $s_{n+1}= \dfrac{1}{3} s_n+ \dfrac{2}{3} x_n$.

  2. Reproduire et compléter le tableau ci-dessous, en indiquant les six premières valeurs de $t=nT_e$ et $s_n$.

    $n$ $n\lt 0$ 0 1 2 3 4 5
    $t=nT_e$ (en ms) $t\lt 0$
    $x_n$ 0 3 3 3 3 3 3
    $s_n$ 0

  3. Quelle est, alors, la valeur en régime permanent de $(s_n)$ notée $s_ {perm}$, sachant que pour $t$ tendant vers l’infini, $s_n=s_{n-1}=s_{n-2}=...=s_{perm}$ ?

  4. On admet que, pour tout entier naturel $n$, $s_n=3-3\left(\dfrac{1}{3}\right)^n$.
    Déterminer la transformée en $Z$ du signal causal $s$.

Partie C : Comparaison du signal analogique et du signal discret :

  1. Compléter la ligne donnant les valeurs de $s_n$ dans le tableau ci-dessous (arrondir à $10^{-3}$ près) pour comparer les réponses à l’échelon unité du système analogique et du système numérique.

    $n$ 0 1 2 3 4 5 10 100
    $s_n$ 0 2.667 2.889
    $t=0.01n$ 0 0.01 0.02 0.03 0.04 0.05 0.10 1
    $s(t)$ 0 2.594 2.999

  2. Comparer les comportements à très long terme des signaux obtenus dans chacune des parties en calculant chacune des limites.

On considère une chasse d'eau connectée permettant d'analyser et de réduire la consommation d'eau dans les toilettes d'une station service sur autoroute.

Quand le réservoir est vide, la vanne est grande ouverte : le débit d'arrivée d'eau est maximal : le débit est maximal. Au fur est à mesure que le réservoir se remplit, la vanne se referme afin que le débit diminue progressivement jusqu'à l'arrêt complet.

La hauteur d'eau $h(t)$ à l'instant $t$ lorsque le réservoir se remplit est solution de l'équation différentielle $y'+0.05y=0.015$ avec $y(0)=0$.

Partie A : signal analogique :

  1. Déterminer, à l'aide de Xcas, la solution $h$ l'équation différentielle $y'+0.05y=0.015$ avec $y(0)=0$.

  2. Déterminer la limite $L$ de $h$ en $+\infty$.

  3. La vanne se ferme lorsque la hauteur atteint 99% de la hauteur limite $L$. Déterminer le temps d'ouverture de la vanne.

Partie B : échantillonnage :

Afin de vérifier le bon remplissage du réservoir et savoir si le niveau d'eau est suffisant lors de l'utilisation suivante, un capteur envoie un signal causal numérique discret $(y(n)e(n))$.

Ce signal correspond à la hauteur $h$ échantillonnée suivant le procédé suivant :

  1. Montrer que la relation de récurrence peut s'écrire $y(n+1)= \dfrac{100}{101} y(n)+ \dfrac{3}{1010}$.

  2. Compléter le tableau de valeurs ci-contre :

    $n$ $n\lt 0$ 0 1 2 3 4 5
    $t=nT_e$ (en s) $t\lt 0$
    Sortie $y(n)$ $0$

  3. On admet que pour tout entier naturel $n$ : $y(n)=0.3\left(1-\left(\dfrac{100}{101}\right)^n\right)$.

    1. Déterminer la transformée en $z$ du signal causal $y$.

    2. Déterminer la limite $L_y$ de $y(n)$ quand $n$ tend vers $+\infty$.

    3. Avec le système numérique, la vanne se ferme lorsque la hauteur atteint 99% de la hauteur limite $L_y$. Déterminer le temps d'ouverture de la vanne.

Partie C : Comparaison du signal analogique et du signal discret :

  1. Comparer les temps d'ouverture de la vanne obtenu dans les deux cas.

Demander le programme !


Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲