L'algorithme des $k$ plus proches voisins est dans la section Algorithmique.
- Contenus : algorithme des $k$ plus proches voisins
- Capacités attendus : écrire un algorithme qui prédit la classe d’un élément en fonction de la classe majoritaire de ses k plus proches voisins.
- Commentaires : Il s’agit d’un exemple d’algorithme d’apprentissage.
Introduction à l'algorithme des $k$ plus proches voisins
L’algorithme des $k$ plus proches voisins est l’un des algorithmes utilisés dans le domaine de l’intelligence artificielle.
C'est un algorithme d'apprentissage automatique supervisé qui attribue une catégorie à un élément en fonction de la
classe majoritaire des ses plus proches voisins dans l'échantillon d'entraînement.
Son principe peut être résumé par cette phrase : Dis-moi qui sont tes amis et je te dirai qui tu es.
Cet algorithme d'apprentissage automatique est par exemple utilisé par des entreprises d'Internet comme Amazon, Netflix, Spotify ou iTunes afin de prévoir si vous seriez ou non intéressés par un produit donné en utilisant vos données et en les comparant à celles des clients ayant acheté ce produit particulier.
Cet algorithme a été introduit en 1951 par Fix et Hodges dans un rapport de la faculté de médecine aéronautique de la US Air Force.
Exemple introductif
Dans cette introduction, nous considérons un jeu de données constitué de la façon suivante :
-
les données sont réparties suivant deux types : le type 1 et le type 2,
-
les données n'ont que deux caractéristiques : caractéristique 1 et caractéristique 2,
Imaginez la situation suivante dans un jeu :
-
Vous avez deux types de personnages : les fantassins (type 1 : "fantassin") et les chevaliers (type 2 : "chevalier").
-
Vous avez deux types de caractéristiques : la force (caractéristique 1 : nombre entre 0 et 20) et le courage (Caractéristique 2 : nombre entre 0 et 20 ).
-
Vous avez une collection de personnages dont vous connaissez les caractéristiques et le type.
Vous introduisez un nouveau personnage dont vous ne connaissez pas le type. Vous possédez les caractéristiques de ce nouveau personnage. Le but de l'algorithme KNN ($k$ Nearest Neighbors = $k$ plus proches voisins en français) est de déterminer le type de ce nouveau personnage.
Les données sont stockées dans un fichier csv téléchargeable : fichier csv à télécharger
Voici un aperçu des données :
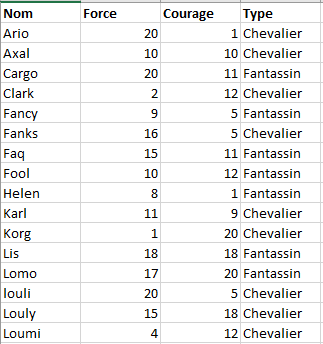
Voici une représentation de ces données :
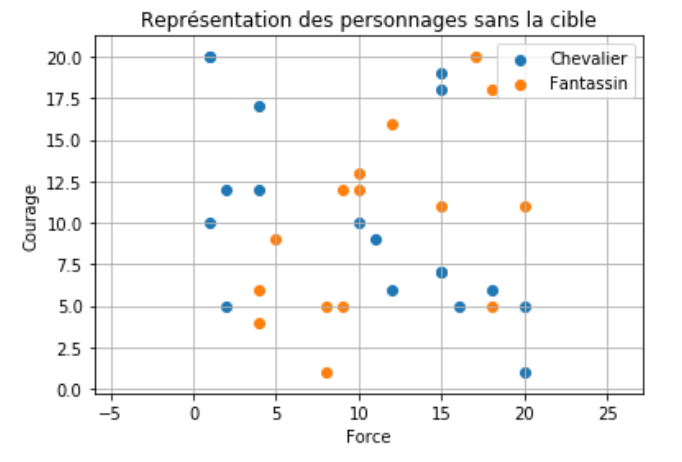
Nous introduisons une nouvelle donnée (appelée cible dans notre exemple) avec ses deux caractéristiques : une force de 12 et un courage de 12,5 . Le but de l'algorithme KNN des $k$ plus proches voisins est de déterminer le type de cette nouvelle donnée.
-
Dans un premier, il faut fixer le nombre de voisins. Nous allons choisir $k$=7.
Voici une nouvelle représentation avec la cible et la recherche des 7 voisins les plus proches proches, ceux qui se trouvent dans le cercle bleu :
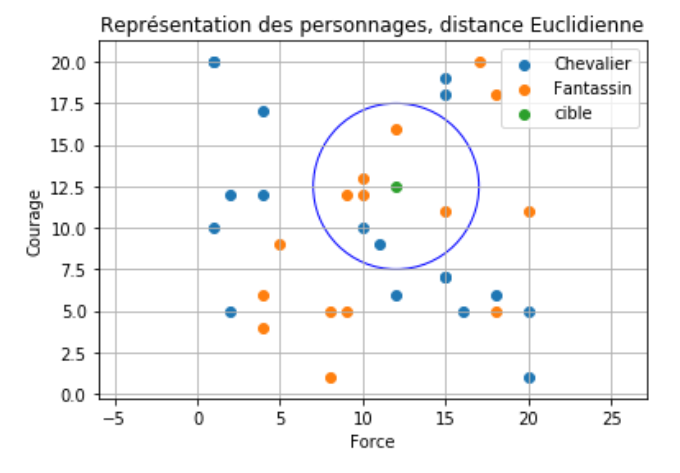
En utilisant les voisins de type "chevalier" et de type "fantassin", déterminer le type le plus probable de notre cible.
-
On considère désormais la valeur $=13$. Voici une nouvelle représentation avec la cible et la recherche des 13 voisins les plus proches proches, ceux qui se trouvent dans le cercle bleu :
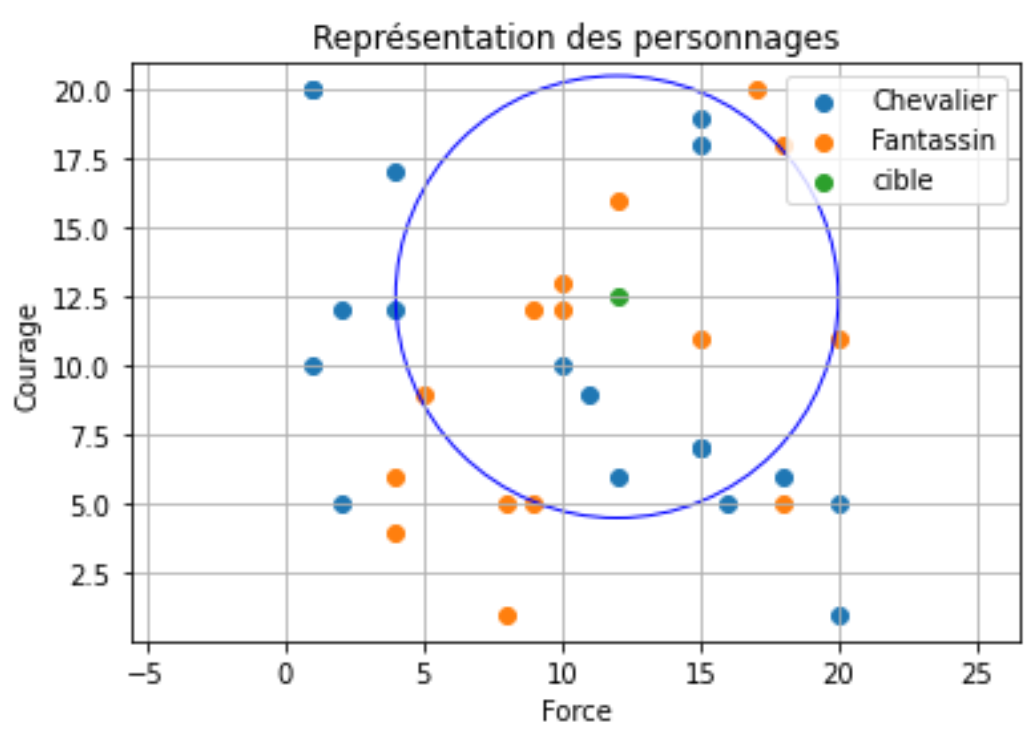 Déterminer le type le plus probable de notre cible dans ce cas ?
Déterminer le type le plus probable de notre cible dans ce cas ?
-
La valeur $k$=7 est ici un choix arbitraire. Cette valeur doit néanmoins être choisie judicieusement : trop faible, la qualité de la prédiction diminue ; trop grande, la qualité de la prédiction diminue aussi. Il suffit d'imaginer qu'il existe une classe prédominante en nombre. Avec une grande valeur de $k$, cette classe remporterait la prédiction à chaque fois.
-
Nous avons utilisé une distance schématisée par un disque. Ce choix est discutable. Il faut faire attention à la distance euclidienne qui n'a de sens que dans un repère orthonormé. Nous aurions pu choisir une autre distance.
-
Il est facile de représenter graphiquement les données avec 1 à 3 caractéristiques. Nous ne pouvons pas représenter des données avec des caractéristiques supérieures à 3 mais l'algorithme reste opérationnel.
L'algorithme
Pour prédire la classe d’un nouvel élément, il faut des données :
-
Un échantillon de données ;
-
Un nouvel élément dont on connaît les caractéristiques et dont on veut prédire le type ;
-
La valeur de $k$, le nombre de voisins étudiés.
Une fois ces données modélisées, nous pouvons formaliser l'algorithme de la façon suivante :
-
Trouver, dans l’échantillon, les $k$ plus proches voisins de l'élément à déterminer.
-
Parmi ces proches_voisins, trouver la classification majoritaire.
-
Renvoyer la classification_majoritaire comme type cherché de l'élément.
Ce qui nous donne l'algorithme naïf suivant :
-
Données: -
une
tablede données de taille $n$ ; -
une donnée cible ;
-
un entier $k$ plus petit que $n$ ;
-
une règle permettant de calculer la
distanceentre deux données. -
Algorithme: -
Trier les données de la table selon la distance croissante avec la donnée cible.
-
Créer la liste des $k$ premières données de la table triée.
-
Renvoyer cette liste.
Influence de la distance choisie
Nous reprenons le même ensemble de données :

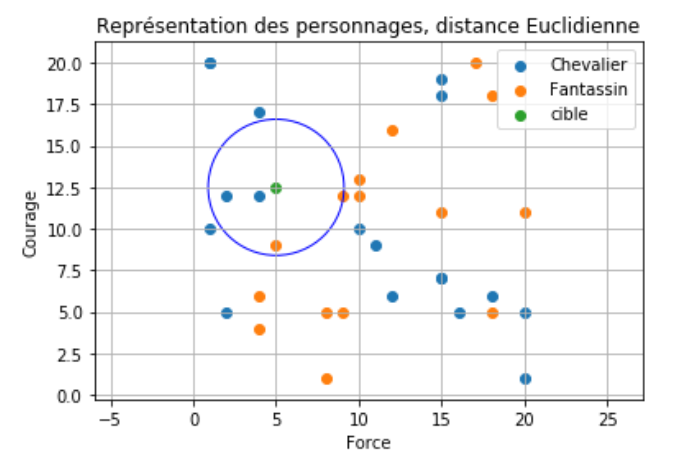
Nous introduisons une cible : force = 5 et courage = 12,5
-
On choisit $k$=4 et la distance schématisée par un disque .
-
Quel est le type de notre donnée cible ? Quel est le problème ?
-
Donner une valeur de $k$ qui permette de décider du type de notre donnée cible ?
-
Donner pour cette valeur de $k$ le type de la donnée cible.
-
-
On choisit $k=9$. Pour la distance, on décide que les valeurs de la force n'ont pas d'importance. La distance dépend du courage.
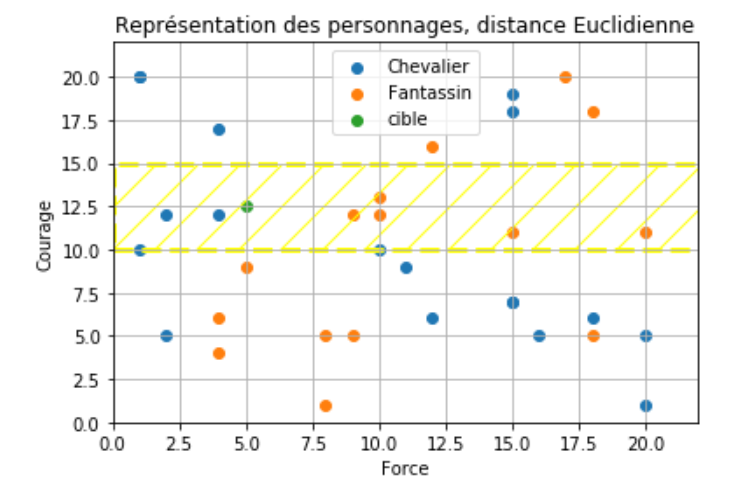
Quel est le type de notre donnée cible ?
-
On choisit $k=5$. Pour la distance, on décide que les valeurs du courage n'ont pas d'importance. La distance dépend de la force.
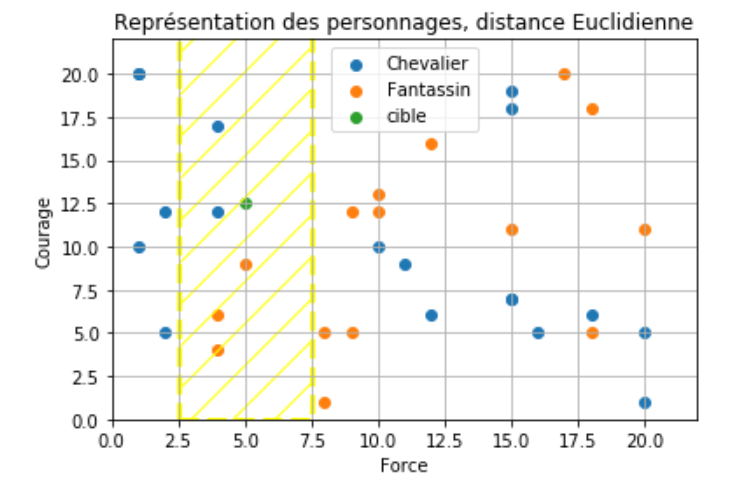
Quel est le type de notre donnée cible ?
Comment représenter ce type de données en Python ?
Les figures précédentes ont été réalisées grâce au module matplotlib, librairie très utile en Python.
-
-
Tester le script Python suivant :
from math import * import matplotlib.pyplot as plt # Données de type 1 liste_x_1 = [1, 3, 8, 13] liste_y_1 = [28, 27.2, 37.6, 40.7] # Données de type 2 liste_x_2 = [2, 3, 10, 15] liste_y_2 = [30, 26, 39, 35.5] plt.axis([0, 15, 0, 50]) # Attention [x1, x2, y1, y2] plt.xlabel('Caractéristique 1') # premier commentaire attendu plt.ylabel('Caractéristique 2') plt.title('Représentation des deux types') plt.axis('equal') # Pour avoir un repère orthonormé plt.grid() plt.scatter(liste_x_1, liste_y_1, label='type 1') # second commentaire attendu plt.scatter(liste_x_2, liste_y_2, label='type 2') plt.legend() plt.show() -
Remplacer les deux commentaires attendus par un commentaire expliquant le rôle des fonctions
plt.labeletplt.scatter.
-
-
-
Vous pouvez ajouter des formes (rectangle, ellipse, etc.).
Exécuter le script suivant :
from math import * import matplotlib.pyplot as plt # Données de type 1 liste_x_1 = [1, 3, 8, 13] liste_y_1 = [28, 27.2, 37.6, 40.7] # Données de type 2 liste_x_2 = [2, 3, 10, 15] liste_y_2 = [30, 26, 39, 35.5] fig, ax = plt.subplots() plt.axis([0, 15, 0, 50]) # Attention [x1, x2, y1, y2] plt.xlabel('Caractéristique 1') plt.ylabel('Caractéristique 2') plt.title('Représentation des deux types') plt.axis('equal') # pour avoir un repère orthonormé. Faire des tests. plt.grid() plt.scatter(liste_x_1, liste_y_1, label='type 1') plt.scatter(liste_x_2, liste_y_2, label='type 2') plt.legend() # Ajout d'un cercle (ou d'une ellipse) ax.add_artist(plt.Circle((6, 30), 4, edgecolor='b', facecolor='none')) # Ajout d'un rectangle ax.add_artist( plt.Rectangle((6, 0), 2, 50, edgecolor='black', facecolor='none', fill=True, hatch='/', linestyle='dashed', linewidth=3, zorder=1)) plt.show() -
Quel est le rôle du premier argument
(6, 30)de la fonctionplt.Circle? -
Quel est le rôle des trois premiers arguments
(6, 0),2et50de la fonctionplt.Rectangle?
-
Influence de la valeur de $k$ choisie
Sur un champ de bataille de la Première Guerre Mondiale un mémorial a été construit. Afin de réaliser une extension, des
fouilles préventives ont été réalisées par l'INRAP (Institut National de Recherches Archéologiques Préventives).
Au cours de ces fouilles, différents objets ou éléments de squelettes humains ont été trouvés. L'étude de ces découvertes a
permis d'identifier la nationalité de nombreux artefacts retrouvés : soit allemand, anglais ou français.
Le plan ci-dessous représente la zone de fouille et la position des éléments dont l'origine a été identifiée.
L'unité est le mètre.
Un élément d'un squelette a été retrouvé en $(10;4)$ ; il est représenté par un losange couleur magenta sur le plan.
L'objectif est de déterminer une origine probable pour cet élément de squelette avant de le déposer dans un ossuaire.

La distance qui sera prise en compte est la distance dite de Tchebychev. (la définition précise de celle-ci sera donnée
au 2.)
Ce que vous devez seulement savoir sur cette distance pour cet exercice c'est que l'ensemble des points
se trouvant à une distance $r$ d'un point $I$ correspond au pourtour du carré, de centre $I$, de côtés parallèles aux axes et
de longueurs $2r$.
Sur le graphique ci-dessus, le carré dessiné :
-
en rouge correspond ainsi à l'ensemble des points se trouvant à 3 mètres.
-
en noir correspond ainsi à l'ensemble des points se trouvant à 1 mètre.
-
-
À quelle valeur de $k$ correspond le carré noir ?
-
Quelle serait l'origine de l'élément de squelette en considérant cette valeur de $k$ ?
-
-
On choisit $k=9$. Quelle serait l'origine de l'élément de squelette en considérant cette valeur de $k$ ?
-
On choisit $k=11$. Quelle serait l'origine de l'élément de squelette en considérant cette valeur de $k$ ?
-
Peut-on savoir à coup sûr, en prenant une valeur de $k$ inférieure au égale à 11, si le combattant dont on a trouvé un élément de squelette était un combattant de la Triple-Entente (France + Royaume-Uni + Russie) ou de la Triple-Alliance (Allemagne + Autriche-Hongrie + Italie) ?
L'algorithme des $k$ plus proches voisins, comme tout algorithme d'apprentissage supervisé est soumis aux
biais d'apprentissage.
Un biais d'apprentissage signifie que l'on entraîne un algorithme d'apprentissage sur un ensemble de données qui
conduit à favoriser de manière erronée une catégorie de manière systématique.
Voici deux exemples réels de cas où ce biais d'apprentissage a pu avoir un impact social important :
-
Le groupe Amazon a développé un logiciel d'apprentissage pour aider aux recrutements. Comme l'ensemble des collaborateurs qui a servi de base à l'apprentissage était constitué majoritairement d'hommes, ce logiciel défavorisait systématiquement le recrutement de femmes.
-
La reconnaissance faciale est aussi fondée sur des algorithmes d'apprentissage.
Des études ont montré des préjugés raciaux et déshumanisant dans les conclusions renvoyées par certains logiciels de reconnaissance faciale. En cause, entre autre, un entraînement sur un ensemble de photos mal calibré.
Implémentation de l'algorithme des $k$ plus proches voisins
Pour implémenter cet algorithme, il nous faut :
-
Une table de données. Cette table peut être une liste ou un dictionnaire.
-
Une distance entre deux données.
-
Une cible.
La notion de distance est un élément central de cet algorithme. Voici quelques distances possibles :
La distance euclidienne (dans un repère orthonormé)
Soit deux données $donnee_{1}$ et $donnee_{2}$ de coordonnées données par les tuples respectifs $(x_{1}, y_{1})$ et $(x_{2}, y_{2})$.
$distance(donnee_{1},donnee_{2}) = \sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$
La distance de Manhattan
Soit deux données $donnee_{1}(x_{1}, y_{1})$ et $donnee_{2}(x_{2}, y_{2})$.
$distance(donnee_{1},donnee_{2}) = \lvert{x_{1}-x_{2}}\rvert+\lvert{y_{1}-y_{2}}\rvert$.
La distance de Tchebychev
Soit deux données $donnee_{1}(x_{1}, y_{1})$ et $donnee_{2}(x_{2}, y_{2})$.
$distance(donnee_{1},donnee_{2}) = max(\lvert{x_{1}-x_{2}}\rvert,\lvert{y_{1}-y_{2}}\rvert$).
Voici le début la structure globale de l'algorithme des $k$ plus proches voisins, sachant que :
-
la fonction distance incluse est à préciser,
-
la liste des voisins renvoyée permettra ensuite de déterminer la catégorie majoritaire.
def k_plus_proches_voisins(table, cible, k):
"""Renvoie la liste des $k$ plus proches voisins de la cible"""
def distance_cible(donnee):
""" renvoie la distance entre la donnée et la cible"""
return distance
# On trie la table de manière croissante en utilisant la distance comme critère.
table_triee = sorted(table, key=distance_cible)
# gestion de la liste des k plus proches voisins
proches_voisins = [] # initialisation vide
for i in range(k):
proches_voisins.append(table_triee[i]) # On ajoute les $k$ premières valeurs
return proches_voisins # On renvoie la liste des $k$ plus proches voisins.
# On peut utiliser des listes ou des dictionnaires
table = [['t1', 1, 28], ['t1', 3, 27.2], ['t1', 8, 37.6], ['t1', 13, 40.7], ['t2', 2, 30], ['t2', 3, 26], ['t2', 10, 39], ['t2', 15, 35.5]]
# 't1' représente le type 1
# 't2' représente le type 2
# La première valeur numérique correspond à la valeur de la caractéristique 1
# La deuxième valeur numérique correspond à la valeur de la caractéristique 2
# Caractéristiques 1 et 2 de la cible
cible = [7, 28.4]
# Valeur de $k$
k = 3
def k_plus_proches_voisins(table, cible, k):
"""Renvoie la liste des $k$ plus proches voisins de la cible"""
def distance_cible(donnee):
""" renvoie la distance entre la donnée et la cible"""
distance = abs(donnee[1]-cible[0]) + abs(donnee[2]-cible[1])
return distance
table_triee = sorted(table, key=distance_cible)
proches_voisins = []
for i in range(k):
proches_voisins.append(table_triee[i])
return proches_voisins
k_plus_proches_voisins(table, cible, k)
-
Afficher le résultat de la fonction
k_plus_proches_voisins(table, cible, k). Quel est le type de la cible ? -
Quelle est la valeur de $k$ ?
-
Quelle distance a-t-on utilisée ?
-
Utiliser d'autres valeurs de $k$. Quel est l'effet sur le type de la cible ?
-
Changer la distance. Programmer la distance de Tchebychev. Quel est l'effet sur le type de la cible ?
On considère le code ci-dessous.
from math import *
# from random import *
import matplotlib.pyplot as plt
# import numpy as np
# from scipy.stats import linregress
# Données de type 1
liste_x_1 = [1, 3, 8, 13]
liste_y_1 = [28, 27.2, 37.6, 40.7]
# Données de type 2
liste_x_2 = [2, 3, 10, 15]
liste_y_2 = [30, 26, 39, 35.5]
plt.axis([0, 15, 0, 50]) # Attention [x1, x2, y1, y2]
plt.axis('equal')
plt.xlabel('Caractéristique 1')
plt.ylabel('Caractérstique 2')
plt.title('Représentation des deux types')
plt.grid()
plt.scatter(liste_x_1, liste_y_1, label='type 1')
plt.scatter(liste_x_2, liste_y_2, label='type 2')
plt.scatter(7, 28.4, label='cible')
plt.legend()
plt.show()
table = [['t1', 1, 28], ['t1', 3, 27.2], ['t1', 8, 37.6], ['t1', 13, 40.7], ['t2', 2, 30], ['t2', 3, 26], ['t2', 10, 39], ['t2', 15, 35.5]]
cible = [7, 28.4]
k = 3
def k_plus_proches_voisins(table, cible, k):
"""Revoie la liste des k plus proches voisins de la cible"""
def distance_cible(donnee):
""" renvoie la distance entre la donnée et la cible, on choisit la distance de Manhattan"""
distance = abs(donnee[1]-cible[0]) + abs(donnee[2]-cible[1])
return distance
table_triee = sorted(table, key=distance_cible)
proches_voisins = []
for i in range(k):
proches_voisins.append(table_triee[i])
return proches_voisins
print("La liste des ", k, " plus proches voisins de la cible : ", k_plus_proches_voisins(table, cible, k))
Vous pouvez exécuter ce code directement sur ce trinket.
-
Faire une recherche sur la distance de
Hamming. - Donner la distance de
Hamming:-
entre $100100$ et $100010$ ;
-
entre $210510$ et $201511$ ;
-
entre "maille" et "paille".
-
-
Écrire, en langage Python, une fonction
hammingqui renvoie la distance deHammingentre deux éléments.
Exercices
Chevaliers et fantassins
Le but est d'étudier plus en détail l'exemple qui a servi d'introduction visuelle à l'algorithme des $k$ plus proches voisins.
-
Voici une fonction
impor:import csv def impor(nom): lecteur = csv.DictReader(open(nom + '.csv', "r", encoding='utf-8-sig'), delimiter=";") return [ligne for ligne in lecteur]La fonction
DictReaderdu modulecsvpermet d'ouvrir un fichier csv et de créer un itérable de dictionnaires. La première ligne du fichier csv donne l'ensemble des clés des dictionnaires et chaque autre ligne donnera les valeurs d'un dictionnaire.Si le fichier csv
monty_python.csvest donné par le contenu suivant où chaque élément est séparé par le symbole;nom;prenom Graham;Chapman John;Cleese Terry;Gilliam Eric;Idle Terry;Jones Michael;Palinalors l'instruction
impor("monty_python")renvoie la liste suivante :[{'nom': 'Graham', 'prenom': 'Chapman'}, {'nom': 'John', 'prenom': 'Cleese'}, {'nom': 'Terry', 'prenom': 'Gilliam'}, {'nom': 'Eric', 'prenom': 'Idle'}, {'nom': 'Terry', 'prenom': 'Jones'}, {'nom': 'Michael', 'prenom': 'Palin'}]Expliquer comment utiliser cette fonction afin de récupérer dans une variable nommée
combattantsla liste des personnages associés à leur force, courage et type ; données initialement dans un fichierpersonnages.csvaccessible ici directement.Tester le bon fonctionnement de la fonction avec le fichier
personnages.csvaccessible ici directement.Le fichier
personnages.csvtéléchargé doit être placé au niveau du répertoire courant de travail de votre IDE.
Si vous ne connaissez pas le répertoire courant de travail ou si vous voulez placer le fichier csv dans le même répertoire que le fichier .py contenant la fonctionimpor, il vous suffit tout ou partie du code suivant :import os # import du module permettant d'utiliser les fonctionnalités dépendant du système d'exploitation print(os.getcwd()) # Pour afficher le répertoire courant de travail usuel os.chdir(os.path.dirname(os.path.abspath(__file__))) # pour travailler désormais dans le répertoire du fichier python exécuté print(os.getcwd()) # pour vérifier le répertoire courant de travail modifié -
Proposer une fonction
est_personnagequi prend en paramètres une liste de personnages comme celle renvoyée par la fonction de la question précédente et un nom sous forme de chaîne de caractères. Cette fonction renvoie un booléen donnant l'appartenance ou non d'un personnage portant le nom donné comme argument dans cette liste.Utiliser cette fonction afin de savoir s'il existe un combattant du nom de
"Lis"? -
Trier la table des personnages par le type.
En cas de difficultés, en cliquant ici, il est possible d'obtenir un code à trous à compléter.-
La fonction
sortedpermet de renvoyer une liste triée suivant un critère qui est précisé comme fonction donnée en tant qu'argument de l'attributkey:liste_triee = sorted(liste_initiale, key=fonction_de_critere_prioritaire_de_tri).
Vous trouverez un exemple d'utilisation dans le deuxième exemple de cette page officielle de la documentation du langage Python. -
Vous pouvez utiliser la lambda-fonction
lambda dico: dico["Type"]comme montré dans le cours sur le tri d'une table ou dans la documentation proposée ci-dessus.
Copier puis compléter le script suivant en vous servant des commentaires et du test proposé ci-dessus.
import csv def impor(nom): lecteur = csv.DictReader(open(nom + '.csv', "r", encoding='utf-8-sig'), delimiter=";") return [ligne for ligne in lecteur] combattants = impor(...) # attention à adapter selon l'endroit où a été déposé ou renommé le fichier personnage.csv print(combattants) # pour visualiser la liste des personnages et leurs caractéristiques associées. combattants_tries = sorted(..., key=lambda dico: dico[...]) print(combattants_tries) -
-
Écrire et utiliser l'algorithme des $k$ plus proches voisins avec $k=7$ et la distance euclidienne pour savoir quel sera le type du personnage nommé
"popsi", de force'12'et de courage'12.5'selon la table des personnages connus.En cas de difficultés, en cliquant ici, il est possible d'obtenir un code à trous à compléter.-
Vous pouvez compléter et adapter la forme générale du script proposé dans la propriété 2 de ce chapitre.
-
Pour la distance euclidienne, la fonction
sqrtissue du modulemathsera sûrement nécessaire. -
Pour définir la fonction
distance_cible, vous pouvez utiliser la fonctioneval. Cette fonction peut prendre une chaîne de caractères correspondant à une expression en Python comme argument et renvoie la valeur calculée pour cette expression (cf. documentation officielle).
Copier puis compléter le script suivant en vous servant des commentaires et du test proposé ci-dessus.
import csv def impor(nom): lecteur = csv.DictReader(open(nom + '.csv', "r", encoding='utf-8-sig'), delimiter=";") return [ligne for ligne in lecteur] combattants = impor(...) # attention à adapter selon l'endroit où a été déposé ou renommé le fichier personnage.csv print(combattants) # pour visualiser la liste des personnages et leurs caractéristiques associées. # algorithme des k plus proches voisins : def k_plus_proches_voisins(table, cible, k): """Renvoie la liste des k plus proches voisins de la cible""" def distance_cible(personnage): # choix de la distance """ renvoie la distance entre la donnée et la cible, on choisit la distance euclidienne""" distance = sqrt((eval(...)-eval(...))**2 + (eval(...)-eval(...))**2) return ... table_triee = sorted(table, key=distance_cible) # table triée par ordre croissante en fonction de leur distance à la cible. proches_voisins = [] for i in range(k): proches_voisins.append(...[i]) return proches_voisins # Saisie des données particulières étudiées table = ... # choix de la table k = ... # choix de la valeur de k cible = {'Nom': ..., ...: ..., ...: ...} # personnage popsi à entrer # affichage de la liste des k plus proches voisins : print(k_plus_proches_voisins(table, cible, k)) -
Il est possible de remplacer l'utilisation de la lambda-fonction de la question 3 par la création préalable au tri d'une fonction qui à chaque dictionnaire représentant un personnage associe son type comme ainsi :
# saisir avant le contenu du script du 1.
def ordre_type(dico: dict) - >str: # dico est un dictionnaire représentant un personnage
return dico['Type'] # le type du personnage est renvoyé
combattants_tries = sorted(combattants, key=ordre_type)
print(combattants_tries)
Le but est d'obtenir des graphiques représentant sous forme de nuages de points les données de l'exercice précédent, graphiques similaires à ceux utilisés dans la première partie de ce chapitre.
En abscisse sera placé le niveau de force, en ordonnée celui du courage.
-
Écrire un script qui stocke : dans une variable :
-
liste_chevalier_xla liste des niveaux de force pour les seuls chevaliers -
liste_chevalier_yla liste des niveaux de courage pour les seuls chevaliers -
liste_fantassin_xla liste des niveaux de force pour les seuls fantassins -
liste_fantassin_yla liste des niveaux de courage pour les seuls fantassins
Attention à avoir correctement classé la table afin que les éléments de même index pour chacune des listes correspondent à un même combattant.
-
-
Créer un script qui affichage le nuage de points des personnages de la table en fonction de leur force (en abscisse) et de la courage (en ordonnée).
-
Rajouter le personnage cible nommé "popsi", de force 5 et de courage 12.5 ainsi que le cercle centré sur ce personnage et de rayon 6.
-
Quelle valeur de $k$ correspond à ce cercle ?
Quel type est associé avec cette valeur et cette distance au personnage cible ? -
Modifier le script précédent afin de ne prendre en compte que le niveau de courage : il affiche au lieu du cercle un rectangle de largeur 5, centré en hauteur sur le point cible.
Quel type est associé avec cette valeur et cette distance au personnage cible ?
-
Modifier le script précédent afin de ne prendre en compte que le niveau de force : il affiche au lieu du cercle un rectangle de largeur 5, centré en largeur sur le point cible.
Quel type est associé avec cette valeur et cette distance au personnage cible ?
Harry potter
Source : NSI 1re générale (Numérique et sciences informatiques) - Prépabac, nouveau programme de Première (2020-2021) – Céline Adobet, Guillaume Connan, Gérard Rozsavolgyi, Laurent Signac Lien vers le manuel de chez Hatier Objectif bac page 266
À l’entrée à l’école de Poudlard, le Choixpeau magique répartit les élèves dans les différentes maisons (Gryffondor, Serpentard, Serdaigle et Poufsouffle) en fonction de leur courage, leur loyauté, leur sagesse et leur malice.
Le Choixpeau magique dispose d’un fichier CSV dans lequel sont répertoriées les données d’un échantillon d’élèves. Le fichier ChoixpeauMagique.csv est téléchargeable à cet endroit :
choixpeauMagique.csv
| Nom | Courage | Loyauté | Sagesse | Malice | Maison |
|---|---|---|---|---|---|
| Adrian | 9 | 4 | 7 | 10 | Serpentard |
| Andrew | 9 | 3 | 4 | 7 | Gryffondor |
| Angelina | 10 | 6 | 5 | 9 | Gryffondor |
| Anthony | 2 | 8 | 8 | 3 | Serdaigle |
On souhaite que Choixpeau magique oriente :
| Nom | Courage | Loyauté | Sagesse | Malice |
|---|---|---|---|---|
| Hermione | 8 | 6 | 6 | 6 |
| Drago | 6 | 6 | 5 | 8 |
| Cho | 7 | 6 | 9 | 6 |
| Cédric | 7 | 10 | 5 | 6 |
-
Modéliser un élève
On modélise un élève par un dictionnaire.
Exemple :
{'Nom': 'Bellatrix', 'Courage': 10, 'Loyauté': 4, 'Sagesse': 9, 'Malice': 9, 'Maison': 'Serpentard'}.-
Donner la modélisation de l'élève Anthony.
-
On utilise la distance de Manhattan.
-
Vérifier à la main que la distance entre Hermione et Adrian est égale à 8.
-
Quelle est la distance entre Angelina et Drago ?
-
Écrire le code d'une fonction distance qui prend deux élèves en paramètre et qui renvoie la distance entre ces deux élèves. Ne pas oublier de préciser la documentation et donner au moins un test.
-
-
- Charger les données de la table
Se reporter au chapitre sur les tables afin d'écrire une fonction qui permet de récupérer les données des élèves d'un fichier CSV pour les stocker dans une liste. On doit obtenir une liste de dictionnaires.
- Trouver la maison majoritaire
-
Écrire une fonction
frequence_des_maisons(table)qui prend en paramètre une table d'élèves et qui renvoie le dictionnaire des fréquences des maisons. Vous devez obtenir :{'Serpentar': 12, 'Gryffondor': 17, 'Serdaigle': 11, 'Poufsouffle': 10}. -
Écrire une fonction
maison_majoritaire(table)qui prend en paramètre une table d'élèves et qui renvoie le nom de la maison la plus représentée.
-
-
Algorithme des 7 plus proches voisins
On dispose d'une
tableet d'une nouvelle élèveNiuequi n'a pas encore de maison. On sait que cette élève est de "Courage" de niveau 7, de "Loyauté" de niveau 8, 5 en niveau de "Sagesse" et 4 en niveau de "Malice".
On cherche les 7 plus proches voisins de ce nouveau.-
Écrire l'algorithme des 7 plus proches voisins.
-
Implémenter cet algorithme en python.
-
Faire un test avec 'Hermione'. Vous devez obtenir les 7 voisins suivants :
[{'nom': 'Cormac', 'Courage': 9, 'Loyauté': 6, 'sagesse': 5, 'malice': 4, 'maison': 'Gryffondor'}, {'nom': 'Milicent', 'Courage': 9, 'Loyauté': 3, 'sagesse': 5, 'malice': 6, 'maison': 'Serpentar'}, {'nom': 'Neville', 'Courage': 10, 'Loyauté': 5, 'Sagesse': 6, 'Malice': 4, 'Maison': 'Gryffondor'}, {'nom': 'Padma', 'Courage': 6, 'Loyauté': 6, 'Sagesse': 6, 'Malice': 9, 'Maison': 'Serdaigle'}, {'nom': 'Susan', 'Courage': 5, 'loyauté': 6, 'Sagesse': 5, 'malice': 5, 'Maison': 'Poufsouffle'}, {'nom': 'Angelina', 'Courage': 10, 'loyauté': 6, 'Sagesse': 5, 'Malice': 9, 'Maison': 'Gryffondor'}, {'nom': 'Colin', 'Courage': 10, 'Loyauté': 7, 'Sagesse': 4, 'Malice': 7, 'Maison': 'Gryffondor'}]La maison attribuée pour 'Hermione' est 'Gryffondor'.
-
- Attribuer une maison
On dispose d'une
tableet de cette nouvelle élèveNiuequi n'a pas encore de maison. On sait que cette élève est de "Courage" de niveau 7, de "Loyauté" de niveau 8, 5 en niveau de "Sagesse" et 4 en niveau de "Malice".
On cherche désormais à lui attribuer une maison.Implémenter en python l'algorithme de l'attribution :
-
Trouver dans la table les 7 plus proches voisins de cette nouvelle élève.
-
Parmi ces proches voisins, trouver la maison majoritaire.
-
Renvoyer la maison majoritaire pour cette élève "Niue".
Faire un test avec 'Hermione'. Vous devez obtenir comme maison "Gryffondor".
-
On décompose l'exercice en 5 parties :
Pokemon : exercice facultatif
Source : NSI 1re générale (Numérique et sciences informatiques) - Prépabac, nouveau programme de Première (2020-2021) – Céline Adobet, Guillaume Connan, Gérard Rozsavolgyi, Laurent Signac Lien vers le manuel de chez Hatier Exercice page 246
Vous avez ci-dessous à disposition un fichier csv dans lequel vous avez environ 400 Pokemon répartis selon 18 types.
fichier csv à téléchargerJe vous donne un nouveau Pokemon : Hippodocus qui possède les caractéristiques suivantes :
-
points de vie = 108 ;
-
attaque=112 ;
-
défense = 118 ;
-
vitesse= 47.
Questions :
-
Quel type pouvez-vous attribuer à ce Pokemon ?
-
Varier les valeurs de $k$ et les différents types de distances. Le résultat reste-il stable ?
Observer la table "pokemon", surtout les effectifs des différents types.
Pensez-vous que la table soit efficace pour entrainer une intelligence artificielle à la reconnaissance des types pokemon ?
Complexité/coût de l'algorithme KNN
La complexité est abordée dans le chapitre A2 : complexité d'un algorithme.
La complexité de l'algorithme KNN repose sur la complexité du tri de la table.
D'après la documentation du langage Python, le tri de la table dans sortedselon la key distance est en
$ O(n\log(n))$. Cela veut dire que son coût est comparable à $n \log(n)$ ($n$ est la taille de la table à trier).
Dans ce cas on parle de complexité quasi-linéaire.
Première approche du coût d'un algorithme :
Le coût d'un algorithme dépend du nombre d'opérations élémentaires (arithmétiques ou logiques) ainsi que d'affectations nécessaires à son exécution.
Le coût dépend de la donnée elle-même. Dans notre cas, la donnée est une table et la complexité est celle du tri croissant de la table. Si la table est déjà triée, il n'y aura aucun tri à effectuer, on a une situation très favorable. Inversement, on peut facilement imaginer une situation très défavorable (table triée dans l'ordre décroissant).
On parle de plusieurs types de complexité :
-
>La complexité dans le meilleur des cas : c'est la situation la plus favorable.
-
La complexité dans le pire des cas : c'est la situation la plus défavorable.
-
La complexité moyenne.
Dans l'algorithme naïf, on admet que le temps mis pour déterminer les 5 plus proches voisins d’une cible dans un échantillon de taille 10 est de 1 ms. Vérifier que le temps mis pour déterminer les 5 plus proches voisins d'une cible dans un échantillon de taille 50 est de 8,5 ms de taille 50 000 de 23 494 ms.
-
penser à calculer les valeurs de $n \log(n)$ pour $n=10$ ; $n=50$ et $n=50 000$;
-
penser à faire un tableau de valeurs.
Pour les curieux : vers l'intelligence artificielle et le machine learning
Le machine learning est un concept utilisé en intelligence artificielle. Il s'agit d'entraîner une machine à apprendre à reconnaitre certaines formes. On utilise une base d'entraînement pour la machine. L'algorithme knn donne une méthode qui permet d'utiliser cette base d'entrainement.
On vous propose une approche de reconnaissance des chiffres :
Aperçu du fichier principal :
Il y a plusieurs fichiers à télécharger, outre le fichier principal, pour utiliser ce fichier:
- fichier principal Jupyter à exécuter par étapes une fois téléchargé
- le fichier d'entraînement à télécharger et à installer dans votre répertoire courant de travail
- le fichier de tests à télécharger et à installer de même
Merci à Goery Valance pour avoir accepté de partager dans cette partie ses documents.
QCM
Questions issues de la Banque Nationale de Sujets
Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC
Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).
On a représenté sur un quadrillage les éléments de quatre classes (chaque classe est représentée par un carré,
un triangle, un losange ou un disque) ainsi qu’un nouvel élément X.
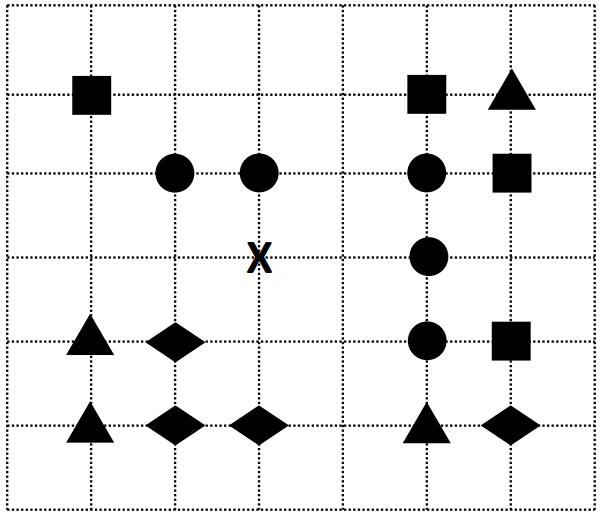
En appliquant l'algorithme des $k$ plus proches voisins pour la distance usuelle dans le plan, avec $k=5$, à quelle classe est affecté le nouvel élément X ?
Réponses :
A- La classe des carrés.
B- La classe des triangles.
C- La classe des losanges.
D- La classe des disques.
Une seule des affirmations suivantes est vraie :
Réponses :
A- L'algorithme des $k$ plus proches voisins a pour but de déterminer les $k$ plus proches voisins d'une observation dans un ensemble de données.
B- L'algorithme des $k$ plus proches voisins a pour but de déterminer la classe d'une observation à partir des classes de ses $k$ plus proches voisins.
C- L'algorithme des $k$ plus proches voisins a pour but de déterminer dans un ensemble de données le sous-ensemble à $k$ éléments qui sont les plus proches les uns des autres.
D- L'algorithme des $k$ plus proches voisins a pour but de déterminer les éléments d'un ensemble de données appartenant à une même classe.
On dispose d’une table de données de villes européennes. On utilise ensuite l’algorithme des $k$ plus proches
voisins pour compléter automatiquement cette base avec de nouvelles villes.
Ci-dessous, on a extrait les 7 villes connues de la base de données les plus proches de Davos.
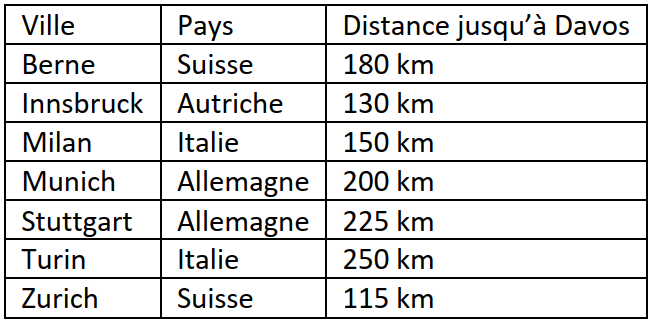
En appliquant l’algorithme des 4 plus proches voisins, quel sera le pays prédit pour la ville de Davos ?
Réponses :
A- Allemagne.
B- Autriche.
C- Italie.
D- Suisse.
À quelle catégorie appartient l’algorithme des $k$ plus proches voisins ?
Réponses :
A- Algorithmes de tri.
B- Algorithmes gloutons.
C- Algorithmes de recherche de chemins.
D- Algorithmes de classification et d’apprentissage.
Autres QCM
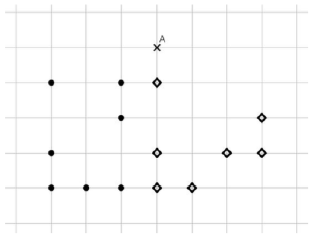
Dans le quadrillage ci-dessous 14 points sont dessinés, dont 7 de la classe C1, avec des ronds noirs •, et 7 de la classe C2, avec des losanges ◇.
On introduit un nouveau point A, dont on cherche la classe à l'aide d'un algorithme des $k$ plus proches voisins pour la distance géométrique habituelle,
en faisant varier la valeur de $k$ parmi 1, 3 et 5.
Quelle est la bonne réponse (sous la forme d'un triplet de classes pour le triplet (1, 3, 5) des valeurs de $k$) ?
Réponses :
A- C1, C2, C3.
B- C2, C1, C2.
C- C2, C2, C2.
D- C2, C1, C1.
Soient les points de coordonnées suivantes :
A(4, 2)
B(1, 5)
C(3, 2)
D(2, 0)
E(7, 6)
F(6, 3)
G(6, 2)
H(8, 5)
En utilisant la distance euclidienne, quels sont les deux plus proches voisins du point I(4, 5) ?
Réponses :
A- Les points A et B.
B- Les points C et D.
C- Les points E et F.
D- Les points G et H.
Dans quel ordre s'effectue les étapes de l'algorithme des k plus proches voisins ?
Réponses :
A- 1. Calculer les distances entre l’élément inconnu et tous les autres points ;
2. Trier les distances, par ordre croissant ;
3. Retenir les k plus courtes distances ;
4. Dénombrer la classe majoritaire ;
5. Attribuer la classe majoritaire à l’élément inconnu.
B- 1. Retenir les k plus courtes distances ;
2. Calculer les distances entre l’élément inconnu et tous les autres points ;
3. Trier les distances, par ordre croissant ;
4. Dénombrer la classe majoritaire ;
5. Attribuer la classe majoritaire à l’élément inconnu.
C- 1. Attribuer la classe majoritaire à l’élément inconnu ;
2. Calculer les distances entre l’élément inconnu et tous les autres points ;
3. Retenir les k plus courtes distances ;
4. Trier les distances, par ordre croissant ;
5. Dénombrer la classe majoritaire.
D- 1. Trier les distances, par ordre croissant ;
2. Retenir les k plus courtes distances ;
3. Calculer les distances entre l’élément inconnu et tous les autres points ;
4. Dénombrer la classe majoritaire ;
5. Attribuer la classe majoritaire à l’élément inconnu.
Générateur aléatoire de questions sur ce chapitre
Il faut actualiser la page pour changer de question. Propriétaire de la ressource : le site GeNumsi en licence CC BY_NC-SA
Sitographie/Bibliographie
NSI 1re générale (Numérique et sciences informatiques) - Prépabac, nouveau programme de Première (2020-2021) – Céline Adobet, Guillaume Connan, Gérard Rozsavolgyi, Laurent Signac Lien vers le manuel de chez Hatier.
Savoir et savoir-faire
-
Savoir que l’algorithme des k plus proches voisins est un algorithme d’apprentissage supervisé.
-
Connaître le fonctionnement de l'algorithme des $k$ plus proches voisins.
-
Savoir définir quelques distances différentes.
-
Savoir que la catégorie attribuée dépendant de la distance et du nombre k de voisins choisis.
-
Savoir écrire l'algorithme des $k$ plus proches voisins.
-
Trouver la classe d'un élément en fonction de la classe majoritaire de ses $k$ plus proches voisins.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International