B2 : codage des entiers relatifs en binaire

Une première représentation intuitive

Une première idée serait de coder le signe $\color{red}{+}$ par un $\color{red}{0}$ et le signe $\color{red}{-}$ par un $\color{red}{1}$.
Ainsi, comme l'écriture binaire de l'entier naturel $\color{blue}{6}$ est $6_{10}=\color{blue}{110}_{2}$ se coderait alors en $\color{red}{0}\color{blue}{110}_{2}$. Mais $\color{red}{-}\color{blue}{6}_{10}$ se coderait alors en $\color{red}{1}\color{blue}{110}_{2}$.

Représentez $14_{10}$ en binaire. Que remarquez vous?

Par conséquent nous allons devoir pour fixer un nombre de bits, $n$, un espace mémoire. On conserve alors le premier pour le signe et les $n-1$ autres pour le codage de la valeur absolue du nombre.

Ainsi sur 8 bits $\color{red}{-}\color{blue}{6}_{10}$ se code en $\color{red}{1}\color{blue}{0000110}$.

Déterminer le codage en binaire sur 8 bits puis sur 9 bits, des nombre suivants :

$11$
$-35$
$26$

Un premier problème avec cette représentation est que le chiffre $\color{blue}{0}_{10}$ a deux représentations. En effet sur 3 bits: $0_{10}=\color{red}{0}\color{blue}{00}_{2}$ et $0_{10}=\color{red}{1}\color{blue}{00}_{2}$.

Un autre problème se pose avec cette méthode sur l'addition de deux nombres en binaires.

Reprendre la représentation en binaire de $-35$ sur 8 bits et l'ajouter à la représentation de $35$ sur 8 bits.

Oubliez donc cette option !

Le complément à deux

Cas des entiers naturels

La représentation d'un nombre entier naturel en binaire se fait de la même manière que dans le paragraphe précédent.

Représentation binaire sur $n$ bits des entiers relatifs positifs

Si on dispose de $n$ bits :

le premier sera $\color{red}{0}$ pour indiquer que l'entier est $\color{red}{positif}$.
les $\color{blue}{n-1}$ autres seront le codage en binaire de l'entier relatif positif vu comme entier naturel comme vu au chapitre B1.

Si l'on dispose de $n$ bits, nous ne pourrons pas dépasser un entier plus grand que $2^{n-1}-1$.

Nous avons vu dans le chapitre B1 que sur $n$ bits, nous pouvions coder au maximum le nombre $2^n-1$.
Puisque nous ne disposons que de $n-1$ bits, le nombre le plus grand codable sera $2^{n-1}-1$.

Comme $12=8+4$, l'écriture binaire du nombre 12 comme entier naturel est $\color{blue}{1100}$.
Si l'on dispose de 6 bits, on peut représenter $12_{10}$ comme $12_{10}=\color{red}{0}\color{blue}{01100}_{2}$.
Si l'on dispose de 5 bits, on peut représenter $12_{10}$ comme $12_{10}=\color{red}{0}\color{blue}{1100}_{2}$.
Si l'on dispose que de 4 bits, on ne peut tout simplement pas représenter $12_{10}$ en binaire si nous considérons les entiers relatifs car il ne reste que 3 bits pour coder la valeur de $12_{10}$ sans son signe et qu'il en faut au minimum 4 pour l'écrire (avec $\color{blue}{1100}$).

Quel est le plus grand entier naturel codable en considérant un bit pour le signe :

sur 5 bits ?
sur 8 bits ?

Cas des entiers négatifs

Complément à deux des entiers relatifs négatifs

Pour représenter un entier relatif négatif, nous allons utiliser le complément à deux :

Voilà la procédure :

On code la valeur absolue du nombre en binaire.
On remplace tous les 0 par des 1 et les 1 par des 0.
On ajoute 1.

Traitons le cas de $-12$ sur 8 bits :

Écriture en binaire de la valeur absolue :
$12_{10}=1100_2$. Nous sommes sur 8 bits donc il faut écrire $12_{10}=00001100_2$.
Permutation des 0 et des 1 :

On remplace tous les 0 par des 1 et les 1 par des 0 : $00001100_2$ devient $11110011_2$.
Ajout de 1 :

On ajoute 1 :$\begin{array}{rrrrrrrrr} &&&&&&1&1&\\ &1&1&1&1&0&0&1&1&\\ +&0&0&0&0&0&0&0&1\\ \hline\\ &1&1&1&1&0&1&0&0 \end{array}$
Ainsi, $-12_{10}$ a pour représentation binaire en complément à deux $\color{red}{1}\color{blue}{1110100}_{2}$.

Vérifions le résultat en ajoutant -12 et 12 dans leur représentation binaire: $\begin{array}{rrrrrrrrr} 1&1&1&1&1&1&&&\\ &1&1&1&1&0&1&0&0\\ +&0&0&0&0&1&1&0&0\\ \hline\\ 1&0&0&0&0&0&0&0&0 \end{array}$

Nous sommes sur 8 bits donc le 1 bit de poids fort en première position doit être enlevé. Nous retombons bien sur 0.

Déterminer la représentation binaire en complément à deux sur 8 bits de $-19$ ; effectuer ensuite l'addition avec la représentation de 19 en binaire.
Déterminer la représentation binaire en complément à deux sur 16 bits de $-72$ ; effectuer ensuite l'addition avec la représentation de 72 en binaire.
Déterminer la représentation binaire en complément à deux sur 6 bits de $24$.

Le terme complément à deux vient du fait que, sur $n$ bits, le nombre négatif $-x$ est représenté en binaire comme le serait le nombre positif $2^n-x$.

Voici la correspondance entre les nombres binaires de 8 bits codés en complément à deux et les entiers relatifs correspondants :

Écriture binaire	Écriture décimale
00000000	0
00000001	1
00000010	2
...	...
01111110	126
01111111	127
10000000	-128
10000001	-127
10000010	-126
...	...
11111110	-2
11111111	-1

Pour comprendre la position des nombres négatifs par rapport aux nombres positifs dans l'écriture binaire lorsque l'on les représente avec le complément à deux, on peut penser aux horloges :

Lorsque la grande aiguille pointe vers le chiffre 8, on peut dire :

qu'il est 40, si on considère le nombre positif de minutes écoulées depuis la dernière heure entière,
ou qu'il est -20, si on considère le nombre de minutes nécessaires pour atteindre la prochaine heure entière.

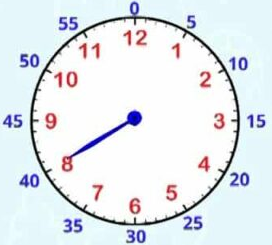
On peut considérer la même chose avec des horloges avec $2^n$ valeurs possibles (au lieu de 12) et ayant comme première valeur 0 (au lieu de 1).
Par exemple avec 8 valeurs possibles :
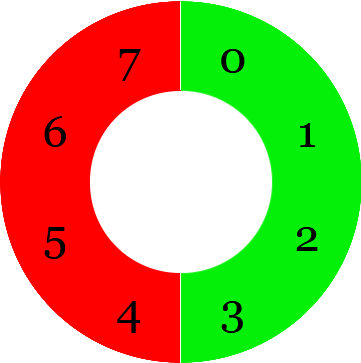
En regardant la partie de gauche comme le nombre de "minutes" pour revenir à 0, on a :
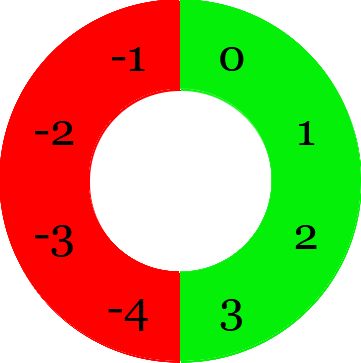
Ce qui donne bien en binaire : 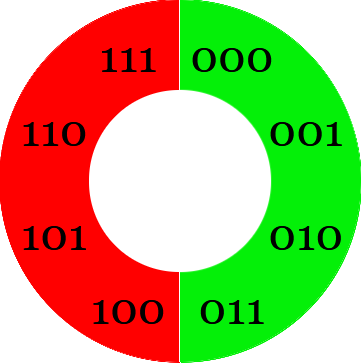et ce aussi bien si l'on considère l'écriture binaire des nombres entiers naturels (positifs), que la représentation binaire en complément à deux des nombres relatifs.

Lien vers une animation permettant de visualiser cela sur d'autres valeurs.

Il faut bien distinguer le nombre binaire de sa représentation en binaire !

Le nombre binaire $1100_{2}$ correspond à l'entier naturel $12_{10}$.
La représentation binaire en complément à deux $1100_{2}$ correspond à l'entier relatif $-4_{10}$.

Avec $n$ bits nous pouvons coder uniquement $2^n$ entiers, ceux compris entre $-2^{n-1}$ et $2^{n-1}-1$

Nous avons vu dans le chapitre B1 que sur $n$ bits, nous pouvions coder $2^n$ entiers.
Puisque le premier bit est réservé au signe de l'entier, nous ne disposons que de $n-1$ bits pour la suite.
Avec 0 comme premier bit, on pourra coder sur les $n-1$ bits restants les $2^{n-1}$ premiers positifs (ou nuls) : ceux entre $0$ et $2^{n-1}-1$.
Avec 1 comme premier bit, on pourra coder sur les $n-1$ bits restants les $2^{n-1}$ premiers strictement négatifs : ceux entre $-1$ et $-2^{n-1}$

Sur 8 bits, donner un encadrement des entiers relatifs codables.
Même question sur 9 bits.

Voici une méthode pour trouver l'écriture décimale d'un nombre entier relatif dont on a le représentation binaire en complément à deux :

Si le bit de poids est 0, alors le nombre cherché est positif : il suffit d'effectuer la même démarche que celle vue dans le chapitre B1 avec des entiers naturels.
Si le bit de poids fort est 1, alors le nombre cherché est négatif : il suffit d'inverser (l'ordre et l'action) des trois étapes vues pour la conversion de décimale vers binaire, plus précisément, il suffit de :
- Étape 1 : commencer par soustraire 1.
- Étape 2 : changer les 0 en 1 et les 1 en 0.
- Étape 3 : convertir en décimal le nombre binaire obtenir.
Attention à ne pas oublier le signe "-" lors de la conclusion.

Déterminer l'écriture décimale du nombre entier relatif dont la représentation binaire en complément à deux est donnée par $11010011_2$.

Code de déblocage de la correction :
Déterminer l'écriture décimale du nombre entier relatif dont la représentation binaire en complément à deux est donnée par $01110111_2$.

Code de déblocage de la correction :
Déterminer l'écriture décimale du nombre entier relatif dont la représentation binaire en complément à deux est donnée par $10011001_2$.

Code de déblocage de la correction :

De nombreuses machines suivent la norme IEEE 1003, appelée aussi norme POSIX. Cette norme spécifie entre autres que le temps est représenté comme le nombre de secondes écoulées depuis depuis le 1er janvier 1970 à 00:00:00 en temps universel.
La plupart des systèmes d'exploitation fonctionnant en 32 bits représente ce nombre de secondes comme un entier signé (nombre binaire utilisant le complément à 2) de 32 bits.

Déterminer le plus grand entier naturel qui peut être représenté sur 32 bits dans le cas du complément à 2 ?
Pourquoi parle-ton "du bug de l'an 2038" ?
Désormais, la plupart des système d'exploitation fonctionnent en 64 bits. Est-ce que cela conduira à un bug en 2106 puisque l'écart entre 1970 et 2038 étant de 68 ans et $2106=2038+68$ ?

Dans le langage Python, le type de données int est utilisé pour représenter des entiers, qui peuvent être négatifs, nul ou positifs.

Dans d'autres langages, comme par exemple le langage C, il est possible de manipuler des entiers avec des représentations diverses adaptées à différents contextes et besoins.
Par exemple :

En C, le type int peut représenter des valeurs négatives, positives et nulles.
Comme par défaut ces entiers sont codés sur 32 bits, la plage des entiers que l'on peut définir avec de type est l'ensemble des entiers compris entre $-2^31$ et $2^31-1$.
Le bit le plus à gauche est utilisé comme bit de signe, où 1 indique une valeur négative et 0 une valeur positive.
En C, le type unsigned int peut représenter des valeurs positives et nulles.
Comme par défaut ces entiers sont codés sur 32 bits, la plage des entiers que l'on peut définir avec de type est l'ensemble des entiers compris entre $0$ et $2^32-1$.
Aucun bit n'est réservé pour le signe, ce qui permet d'utiliser tous les bits pour représenter des valeurs positives.

Du Python pour finir

Écrire une fonction en Python dec_en_binaire(entier, nb_bit) qui convertit un entier naturel en binaire. La fonction renverra l'écriture binaire sous forme d'une liste ànb_bit éléments.

Des opérateurs utiles :
- a%b renvoie le reste de la division de a par b,
- a//b renvoie le quotient de la division de a par b,
- l.append(a) ajoute à la liste l l'élément a,
- l.reverse() inverse les éléments d'une liste l.
Pensez à tester en précondition si le nombre saisi comme premier paramètre et bien un nombre entier naturel et si le nombre de bits nb_bits est suffisant ou non ; en cas d'erreur, pensez à afficher un message d'erreur approprié.
Documentez aussi votre fonction !
Testez :

Vous devriez avoir (au message d'erreur près) :

Testez aussi :

Vous devriez avoir (au message d'erreur près) :

L'objectif de cet exercice est d'écrire une fonction en Python dec_relatif_en_binaire(entier, nb_bit) qui convertit un entier relatif en binaire sur nb_bit.

Il faudra penser à gérer le manque de bits et renvoyer un message d'erreur explicite.

Écrire une fonction change_0_en_1(l) qui remplace les 1 en 0 et les 0 en 1 dans une liste ne contenant que des 0 et des 1.

Testez :

Vous devriez avoir :

Code de déblocage de la correction :
Écrire une fonction ajoute_1(lst) qui ajoute 1 à un binaire représenté par une liste de 0 et de 1 (sans prendre en compte un éventuel dépassement).

Testez :

Vous devriez avoir :

Code de déblocage de la correction :
Écrire la fonction dec_relatif_en_binaire(entier, nb_bit).
Vous utiliserez abs() pour la valeur absolue d'un nombre.

Vous utiliserez les fonctions déjà écrites en langage Python :
- dec_en_binaire
- change_0_en_1
- ajoute_1
Testez :

Vous devriez avoir :

Écrire une fonction binaire_en_dec(l) qui a pour argument une liste l correspondant à un entier écrit en binaire et qui renvoie l'entier en écriture décimale.

Testez :

Vous devriez avoir :

Compléter la fonction ci-dessous de sorte qu'elle prenne en paramètre une liste de 0 et de 1 (correspondant à la représentation binaire d'un entier naturel) et qu'elle renvoie la liste représentant le même entier relatif mais diminué de 1.
Attention ! Si la liste représente 0 alors le renvoi doit représenté -1 en complément à deux, donc doit être la liste formée uniquement de 1.

def ote_1(l: list) -> list:
    """fonction qui prend en paramètre une liste de 0 et de 1 correspondant un nombre binaire
    et qui renvoie la liste représentant le nombre binaire diminué de 1."""
    l.reverse()
    lst = []
    i = 0
    while i... and l[i] == ...:
        i = i+1
    if i == len(l): # cas de 0 représenté en complément à 2 
        for j in range(...):
            lst.append(..) 
    else: 
        for j in range(...):
            lst.append(...)
        lst.append(...)
        # autres bits non modifiés:
        for k in range(..., ...):
            lst.append(...)
    lst.reverse()
    return lst

Voici un jeu de tests possibles :

>>>def ote_1([0, 0, 1, 0, 1, 1])
            [0, 0, 1, 0, 1, 0]
>>>def ote_1([0, 0, 0, 1, 0, 0])
[0, 0, 0, 0, 1, 1]
>>>def ote_1([1, 0, 0, 0, 0, 0, 0])
[0, 1, 1, 1, 1, 1, 1]
>>>def ote_1([0, 0, 0, 0, 0, 0, 0, 0])
[1, 1, 1, 1, 1, 1, 1, 1]

Proposer une fonction binaire_comp_en_dec qui prend en paramètre une liste de 0 et de 1 (supposé représentée en complément à deux un entier relatif) et renvoyant la valeur décimale de cet entier relatif.
Voici un jeu de test pour cette fonction :
```
>>>def binaire_comp_en_dec([1, 0, 0, 0, 0, 0])
-32
>>>binaire_comp_en_dec([0, 0, 0, 0, 0, 0, 0, 0])
0
>>>binaire_comp_en_dec([1, 0, 0, 1, 1])
-13  
```
Reprendre la méthode pour convertir une représentation binaire en complément à deux en nombre décimal.

Utiliser les fonctions déjà écrites binaire_en_dec, ote_1 et change_0_en_1.

Écrire une fonction sommer(nb1, nb2, nb_bit) qui prend en paramètres deux entiers nb1 et nb2, qui additionne ces deux nombres à partir de leur écriture décimale, puis qui transforme cette somme en liste de 0 et de 1 correspondant à l'écriture binaire de ce nombre sur nb_bits, enfin qui renvoie ce résultat.

Testez :

Vous devriez avoir :

Écrire une fonction add(nb1, nb2, nb_bit) qui prend en paramètres deux entiers nb1 et nb2, qui transforme ces deux entiers en liste de 0 et de 1 correspondant à l'écriture binaire de ces nombres sur nb_bits, puis qui additionne ces deux nombres à partir de leur écriture binaire, enfin qui renvoie le résultat de la somme en binaire sur nb_bit bits sous forme de liste de 0 et de 1.

Vous pouvez utilisez la fonction dec_relatif_en_binaire.

Testez :

Vous devriez avoir :

Comparer l'exécution de chaque fonction lorsque les arguments donnés sont (23,-35,5).

QCM

Questions issues de la Banque Nationale de Sujets

Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC

Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).

Quelle est la représentation en binaire signé en complément à 2 de l’entier −1 sur un octet ?

Réponses :

A- 1000 0000

B- 1000 0001

C- 1111 1110

D- 1111 1111

Quelle est la plage des valeurs entières (positifs ou négatifs) que l'on peut coder sur un octet (8 bits) en complément à 2 ?

Réponses :

A- -127 à 128

B- -128 à 127

C- -255 à 128

D- -256 à 127

Quelle est la séquence de bit qui représente –25 en complément à 2 sur 8 bits ?

Réponses :

A- 0001 1001

B- 0001 1010

C- 1110 0110

D- 1110 0111

Comment s'écrit le nombre −42 en binaire, sur 8 bits, en complément à 2 ?

Réponses :

A- -0010 1010

B- 1010 1011

C- 1101 0101

D- 1101 0110

À quoi sert le codage en complément à 2 ?

Réponses :

A- à inverser un nombre binaire

B- à coder des nombres entiers négatifs en binaire

C- à convertir un nombre en hexadécimal

D- à multiplier par 2 un nombre en binaire

L'écriture décimale du nombre 1001 1101 écrit sur 8 bits en complément à 2 est :

Réponses :

A- -4

B- -29

C- -99

D- 157

Quelle est la représentation binaire en complément à deux sur huit bits du nombre –3 ?

Réponses :

A- 1000 0011

B- 1111 1100

C- 1111 1101

D- 1 0000 0011

Quel est l'entier codé sur 4 bits en complément à 2 par 1101 ?

Réponses :

A- -6

B- -3

C- 13

D- 14

Soit $𝑛$ l'entier dont la représentation binaire en complément à deux codée sur 8 bits est 0110 1110. Quelle est la représentation binaire de $−𝑛$ ?

Réponses :

A- 0001 0001

B- 0001 0010

C- 1001 0001

D- 1001 0010

Autres QCM

Les QCM suivants sont des QCM modifiés à partir de QCM se trouvant sur le site https://genumsi.inria.fr.

En considérant le complément à 2 sur 4 bits, quel est le résultat du calcul : 2-7 ?

Réponses :

A- 0101

B- 1001

C- 1011

D- le résultat ne peut pas être écrit en complément à 2 sur seulement 4 bits.

En complément à 2 sur 8 bits, quel est l'entier relatif codé par 11010010 ?

Réponses :

A- 210

B- -210

C- 46

D- -46

Que représente 11010 en complément à 2 sur 5 bits ?

Réponses :

A- -6

B- -5

C- 26

D- -26

Générateur aléatoire de questions sur les réseaux

Il faut actualiser la page pour changer de question. Propriétaire de la ressource : le site GeNumsi en licence CC BY_NC-SA

Savoirs et savoir-faire

Savoir que l'on utilise le complément à 2 pour une représentation des entiers relatifs en binaire.

savoir représenter un nombre entier relatif sous forme binaire en complément à 2,
savoir trouver l'entier relatif représenté en complément à 2,
Savoir programmer un script permettant de passer de l'écriture décimale à celle binaire pour un entier relatif.
Savoir programmer un script permettant de passer de l'écriture binaire à celle décimale pour un entier relatif.

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲