Introduction
George Boole (1815-1864) est un logicien, mathématicien, philosophe britannique. Il est le créateur de la logique moderne, fondée sur une structure algébrique et sémantique, que l’on appelle aujourd’hui algèbre de Boole.
Notons B l’ensemble {0; 1} que nous appellerons ici ensemble des booléens
Nous allons dans ce chapitre manipuler quelques opérateurs booléens, c’est à dire des fonctions d’une ou plusieurs variables dans B et à valeurs dans B.
Nous commençons par définir les opérateurs de base et, ou, non. Le nom de ces opérateurs vient de la convention d’associer 0 à “faux” et 1 à “vrai”.
Les variables python de type booléen peuvent prendre deux valeurs : False, True.

Les opérateurs de base
L'opérateur non (not) : la négation
L'opérateur de négation, noté ~ ou ¬ - qui se lit non, est une fonction définie sur B et à valeurs dans B définie par ¬ 0=1 et ¬ 1=0
On représentera souvent la définition d’un opérateur booléen par sa table de vérité qui est plus simplement le tableau de valeurs de cet opérateur :
| x | ¬ x |
|---|---|
| 0 | 1 |
| 1 | 0 |
L'opérateur de négation transforme donc 0 en 1 et 1 en 0 ou encore faux en vrai et vrai en faux.
Ecrire une fonciton Python qui affiche la table précédente. Le 0 sera représenté en python par
False et le 1 par True .
utiliser la fonction not de Python
L'appel de la fonction se fera ainsi :

la réponse attendue est :

Ecrire la fonction non(a) en Python où le paramètre a peut prendre comme argument 0 et 1 et qui renvoie non(a).
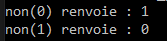
Tester la fonction ainsi :

vous devriez observer :
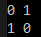
Faites un affichage de sa table de vérité. à l'aide de la fonction non est d'une boucle for.
L'objectif est d'avoir :
L'opérateur et (and) : la conjonction
L'opérateur de conjonction, noté & ou . qui se lit et, est une fonction définie sur B² et à valeurs dans B
Cet opérateur est défini par l'équivalence :
x & y = 1 si et seulement si x et y valent tous deux 1.
- Etablir la table de vérité de l'opérateur &
- Ecrire une fonction Python table_conjonction() qui affiche la table précédente. Le 0 sera représenté en python par
Falseet le 1 parTrue. Utiliser& - Ecrire le script de la fonction
conjontion(x,y)en Python où les paramètresx,ypeuvent prendre comme arguments 0 et 1 et qui renvoiex&y.
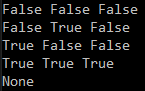
l'appel de la fonction :

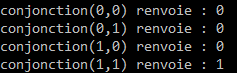
le résultat attendu
les appels de la fonction :
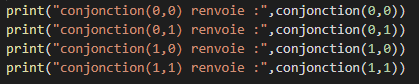
le résultat attendu
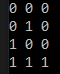
Faites un affichage de sa table de vérité. à l'aide de la fonction conjonction() est d'une boucle for.
L'objectif est d'avoir :
L'opérateur ou (or) : la disjonction
L'opérateur de disjonction , noté | ou + qui se lit ou, est une fonction définie sur B² et à valeurs dans B.
Cet opérateur est défini par l’équivalence :
x | y=1 si et seulement si au moins l’une des deux variables x, y est égale à 1.
On rappelle que le « ou » utilisé en logique est un ou inclusif.
- Etablir la table de vérité de l'opérateur de disjonction
- Ecrire une fonction Python table_disjonction() qui affiche la table précédente. Le 0 sera représenté en python par
Falseet le 1 parTrue. Utiliseror - Ecrire le script de la fonction
disjontion(x,y)en Python où les paramètresx,ypeuvent prendre comme arguments 0 et 1 et qui renvoiex&y.
l'appel de la fonction :

le résultat attendu

les appels de la fonction :

le résultat attendu

Faites un affichage de sa table de vérité. à l'aide de la fonction conjonction() est d'une boucle for.
L'objectif est d'avoir :

Le ou exclusif (xor)
xor, ou exclusif, noté ^ est une fonction définie sur B² et à valeurs dans B
Cet opérateur est défini par l’équivalence :
x ^ y =1 si et seulement si exactement une des deux variables x, y est égale à
1.
Ou encore : x^y=1 si et seulement si x≠y.
Vérifier que x ^ y =( x & ~y ) | (~x & y )
- Etablir la table de vérité de l'opérateur xor
- Ecrire une fonction Python table_xor() qui affiche la table précédente. Le 0 sera représenté en python par
Falseet le 1 parTrue. Utiliser^ - Ecrire la fonction
xor(x,y)en python où les paramètresx,ypeuvent prendre comme arguments 0 et 1 et qui renvoiex^y. - Tester cette fonction en affichant la table de vérité en python
l'appel de la fonction :

le résultat attendu

les appels de la fonction :

le résultat attendu

L'objectif est d'avoir :

Une application : les masques de sous-réseau
Dans un réseau TCP/IP, un ordinateur a une adresse IP qui l’identifie de manière unique (comme un numéro de téléphone), ainsi qu’un masque de sous-réseau.
L’adresse IP et le masque de sous-réseau sont des groupes de 4 entiers positifs, codés
tous les deux sur 4 octets.
Le masque identifie à quel sous réseau d’Internet il fait partie, et permet d’obtenir l’adresse IP du sous-réseau à l’aide d’une opération booléenne.
Pour obtenir l’adresse du sous-réseau de l’ordinateur, on effectue alors un AND entre les octets de l’IP et les octets du masque. En représentation binaire, cela donne :
| IP : | 1 1 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 |
|---|---|
| Masque : | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 |
| AND | |
| adresse de sous-réseau | 1 1 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
Sur un processeur 32 bits, le AND est une opération primitive du processeur, donc l’opération de détermination du sous-masque réseau se fait en une instruction.
Chercher l'adresse IP de votre ordinateur et de son masque sous-réseau. Sous windows, il faut taper la commande ipconfig. Sous linux, il faut taper la commande ifconfig
Chercher l'adresse IP de votre téléphone portable. Vous pouvez vous aider de la fiche : Adresse IP
Ecrire l'adresse des sous-réseaux que vous avez trouvés.
Exercices
mux(x,y,z)=((~x) & y) | (x & z)
Complétez la table suivante:
| x | y | z | ~x | (~x) & y | x & z | mux(x,y,z) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| 0 | 0 | 1 | ||||
| 0 | 1 | 0 | ||||
| 0 | 1 | 1 | ||||
| 1 | 0 | 0 | ||||
| 1 | 0 | 1 | ||||
| 1 | 1 | 0 | ||||
| 1 | 1 | 1 |
1- Dans quel(s) cas l’expression booléenne « x & (~y) » est-elle vraie ?
2- Et pour l’expression « (~x) & (~y) » ?
1- Dans quel(s) cas l’expression booléenne « a | (b & c) » est-elle vraie ?
2- Même question avec l’expression « a | (b & (~c)) » ?
| x | y | ssi(x,y) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Quelques corrections
Vous pouvez télécharger quelques corrections : ici
- Dresser la table d'une expression booléenne
- Réaliser quelques applications directes

NSI de Auteurs : Jean-Christophe Gérard, Thomas Lourdet, Johan Monteillet, Pascal Thérèse est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.