La boucle répétitive for

Rappels sur le pseudo-code

La boucle pour est utilisée quand on connait le nombre de fois où l'on doit répéter une suite d'instructions.

Voici comment écrire cette boucle répétitive dans le cas où on désire $n$ répétitions, $n$ étant un nombre entier naturel non nul.

Structure de la boucle "pour" en pseudo-code :

1 for i←0  to  n-1 
2 	ÉCRIRE i
Pour i allant de 0 à n-1 faire 
Pour i allant de 0 à n-1 faire :
    ...
    les différentes instructions à répéter
    ...    
Fin pour

Autre écriture de la boucle "pour" en pseudo-code :

 for i←0  to  n-1 
    ...
    les différentes instructions à répéter
    ...

On reprend et prolonge un exercice fait dans le chapitre A1 (lien direct)

On veut un algorithme qui donne la somme des $n$ premiers entiers naturels.

Par exemple, pour $n=4$, on veut obtenir la valeur de $0+1+2+3=6$.

Voici une écriture du programme de cet exemple en pseudo-code : 

 
1 S ← 0 
2 for i←0  to  n-1
3    S ← S+i
4 ÉCRIRE S

Pour plus de rappels sur la boucle for en pseudo-code, relire le cours suivant du chapitre A1.

La structure de la boucle for en python avec range

La première ligne fait que la suite du code va être répétée n fois en incrémentant de manière automatique la variable i de 0 à n-1.

Dans un premier temps, nous allons utiliser l'instruction range.

Syntaxe à utiliser pour répéter un bloc d'instruction un nombre $n$ de fois connu à l'avance :

for i in range(n):
    ... 
    les différentes instructions à répéter
    ...

Il y a ainsi trois possibilités pour utiliser l'instruction range, suivant le nombre de paramètres entiers saisis :

On peut réécrire en langage Python, sous forme d'une fonction l'algorithme vu dans l'exemple précédent (lien direct) ainsi : 

def somme(n: int)->int: #les int sont ici pour indiquer le typage des variables d'entrée et de sortie. Ici le paramètre d'entrée est de type int et la sortie également.
    """""La fonction somme renvoie la somme des n premiers entiers naturels.
    la fonction somme a pour attribut un entier (int) : n et renvoie un autre entier :S
    Pour n=4 : S=0+1+2+3+4=10""""" 
    S=0         #initialisation de la somme à 0
    for i in range(n+1):
        S=S+i
    return S

Vous pouvez visualiser la trace d'exécution de cet algorithme grâce au pythontutor ci-dessous :

  1. Modifier la fonction somme de l'exemple précédent en une fonction somme1 qui renvoie la somme des $n+1$ premiers entiers naturels.

    Exemple : pour somme1(4) renvoie 10 car $S=0+1+2+3+4=10$.

  2. Modifier la fonction somme de l'exemple précédent en une fonction somme2 qui prend toujours comme paramètre un entier naturel $n$ et renvoie la somme de tous les nombres entiers impairs inférieurs au égaux à $n$.

    Exemple : pour somme2(6) renvoie 9 car $S=1+3+5=9$.

exercice de renforcement

Écrire une procédure table_multiqui reçoit en entrée un nombre entier $n$ compris entre 0 et 10 et affiche en sortie la table de multiplication de ce nombre.

Par exemple, table_multi(5) conduit à l'affichage suivant (la partie centrale n'a pas été reproduite) :

exercice de renforcement

À la naissance de Crésus, son grand-père Midas, lui ouvre un compte bancaire. Ensuite, à chaque anniversaire, le grand père de Crésus verse sur son compte 100 €, auxquels il ajoute le double de l’âge de Crésus.

Par exemple, lorsqu’elle a deux ans, son grand-père lui verse 104 € ce qui fait un total versé de 100+102+104=306 € à la deuxième année.

Écrire une fonction tresor() qui en entrée reçoit un entier $n$ et en sortie renvoie la somme présente sur le compte de Crésus à sa $n^{ième}$ année écoulée entièrement.

exercice de renforcement

for avec un itérable

Dans la partie précédente, l'instruction range(m,n) créé un ensemble de nombres dont le compteur i parcourait les valeurs.

Un tel ensemble dont un peut parcourir les valeurs avec une boucle for est appelé un itérable.

Au cours de cette années nous verrons progressivement différents itérables :

En Python, pour utiliser un itérable dans une boucle for, il suffit d'utiliser le mot-clé in. Voici la structure générale :

for elt in iterable:
    instruction 1
    instruction 2
    ...

Dans cette boucle, elt va parcourir les éléments de la iterable.

Le programme ci-dessous affiche séparément chaque caractère d'une chaîne de caractères :

# -*- coding: utf-8 -*-
ch="Bonjour à tou.te.s"
for elt in ch:
    print(elt)

Tester le script ci-dessus pour vérifier qu'il réalise bien à ce qui a été annoncé et modifier la chaîne de caractères avec une autre phrase (Vous pouvez aussi rajouter des nombres et des symboles).

  1. Que fait le code suivant :

    # -*- coding: utf-8 -*-
citation="Je ne cherche pas à connaître les réponses, je cherche à comprendre les questions."
compteur=0
for elt in citation:
	if elt=="e":
		compteur=compteur+1
print(compteur)

  2. Transformer le code pour qu'il compte le nombre de i.

  1. Écrire une fonction est_dans_liste qui prend en paramètres une liste lst et un entier n et qui renvoie True si l'entier est dans la liste et False sinon.

  2. Tester la fonction est_dans_liste, entre autres, est_dans_liste([8,4,7,2,5,4],6) renvoie False et est_dans_liste([8,4,7,2,5,4],4) renvoie True.

  3. Proposer au moins deux autres tests pour valider cette fonction sous forme de postconditions.

exercice de renforcement

Voici un programme qui permet de représenter le coût en temps du parcours sur un itérable comme range :

# importation des bibliothèques
from time import perf_counter
import matplotlib.pyplot as plt  

# fonction dont le coût moyen est évalué en fonction de n
def somme(n:int)->int: 
    S=0 #
    for i in range(n+1):
        S=S+i
    return S

# calcul du coût moyen en temps
def temps() -> list:
    Ly = []
    for i in range(11):
        deb = perf_counter() 
        # 100 répétitions du calcul de la somme pour la même valeur de n
        for j in range(100):
            somme(10000*i)
        Ly.append((perf_counter() - deb)/100)  # calcul du temps moyen pour cette valeur de n
    return Ly

# gestion du graphique
Lx = [10000*i for i in range(11)] # création de la liste des abcisses
Ly = temps() # Les différentes valeurs de Ly correspondront aux ordonnées des points 
plt.axis([0,100000, 0, 0.015])    # fenêtre du graphique [x_min,x_max,y_min,y_max]
plt.xlabel("nombre d'entiers additionnées")       # légende de l'axe des abscisses
plt.ylabel('temps moyen nécessaire (en seconde)') # légende de l'axe des orodnnées
plt.title('Coût en temps en fonction du nombre de répétitions')  # titre du graphique
plt.grid()                                # graduation
plt.scatter(Lx,Ly, label='temps moyen')   # nuage de points avec une légende explicative
plt.legend()        # pour faire apparaître la légende explicative précédente
plt.show()          # À ne pas oublier : pour faire appraître le graphique

  1. Exécuter le programme précédent (dans un jupyter-notebook).

    Normalement, vous verrez apparaître un graphique proche de celui-ci :

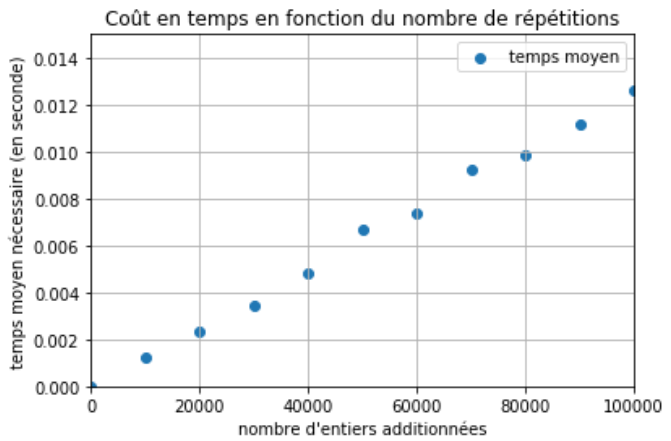
    graphique coût en temps

    Si vous n'avez pas 11 points sur votre graphique, remplacer dans plt.axis([0,100000, 0, 0.015]) 0.015 par un nombre un peu plus grand (tout dépend du processeur de votre ordinateur).

  2. Que pouvez-vous dire quand à la relation liant le temps moyen de calcul et le nombre de répétitions ?

  3. Quel est l'ordre de grandeur du temps moyen que prend une opération comme l'addition sur un ordinateur comme le vôtre ?

Quand le temps de calcul est proportionnel au nombre de répétitions, on dit que le coût en temps est linéaire.

La boucle répétitive while

Rappels sur la boucle répétitive conditionnelle en pseudo-code

La boucle répétitive conditionnelle Tant que / while est utilisée quand on ne connait pas le nombre de fois où l'on doit répéter une suite d'instructions.

Une autre différence majeure avec la boucle pour est l'absence d'incrémentation automatique.

Structure de la boucle "tant que" en pseudo-code :

1 while condition vraie 
2 	bloc d'instructions à répéter

Comment ça marche ?

Dans la boucle while :

Deux écueils à éviter :

On reprend et prolonge un exercice fait dans le chapitre A1 (lien direct)

On veut un algorithme qui donne la somme des $n$ premiers entiers naturels.

Par exemple, pour $n=4$, on veut obtenir la valeur de $0+1+2+3=6$.

Voici une écriture du programme de cet exemple en pseudo-code avec l'instruction répétitive conditionnelle while : 

 
1 S ← 0 
2 i ← 0 
3 while i < n :
4    i ← i+1
5    S ← S+i
6 ÉCRIRE S

Pour plus de rappels sur la boucle while en pseudo-code, relire le cours suivant du chapitre A1.

La boucle répétitive conditionnelle en langage Python

Syntaxe à utiliser avec l'instruction while :

while condition:
   ... 
   les différentes instructions à répéter
   ...

On peut réécrire en langage Python, sous forme d'une fonction l'algorithme vu dans l'exemple précédent (lien direct) ainsi : 

def somme(n: int) -> int: 
    """""La fonction somme renvoie la somme des n premiers entiers naturels.
    la fonction somme a pour attribut un entier (int) : n et renvoie un autre entier :S
    Pour n=4 : S=0+1+2+3=6""""" 
    S = 0 #initialisation de la somme à 0
    i = 0
    while i < n-1:
        i += 1 #o n aurait pu écrire aussi i=i+1 ; incrémente i de 1 à chaque passage dans la boucle     
        S = S+i
    return S

Vous pouvez visualiser la trace d'exécution de cet algorithme grâce au pythontutor ci-dessous :

  1. Modifier la fonction somme de l'exemple précédent en une fonction somme1 qui renvoie la somme des $n+1$ premiers entiers naturels.

    Exemple : pour somme1(4) renvoie 10 car $S=0+1+2+3+4=10$.

  2. Modifier la fonction somme de l'exemple précédent en une fonction somme2 qui prend toujours comme paramètre un entier naturel non nul $n$ et renvoie la somme de tous les nombres entiers impairs inférieurs au égaux à $n$.

    Exemple : pour somme2(6) renvoie 9 car $S=1+3+5=9$.

  3. Rajouter une précondition pour assurer le bon fonctionnement de somme2.

  4. Proposer au moins deux tests pour valider cette fonction.

exercice de renforcement

Une association militant pour la sauvegarde d'une espèce protégée fait appel à un financement participatif. Cette association a besoin de 13500€ pour mener à bien sa campagne annuelle. Elle aimerait savoir combien de jours seront nécessaires pour obtenir la somme de 13500€ en fonction de la somme moyenne recueillie sur le site. Elle fait appel à vous afin que vous lui créiez un programme répondant à la question.

  1. Écrire une fonction attendre qui prend comme paramètre d'entrée un flottant somme indiquant la somme en moyenne recueillie quotidiennement sur le site et renvoie un entier indiquant le nombre de jours nécessaire pour atteindre 13500€.

  2. Proposer des préconditions à cette fonction.

exercice de renforcement

On considère la fonction suivante : 

def repeter(n: int) -> int:
    while n > 10:
        n = n - 10
    return n

Parmi les assertions suivantes lesquelles sont vraies ?

Réponses :

A- On sort de la boucle while dès que n > 10.

B- On sort de la boucle while dès que n < 10.

C- On sort de la boucle while dès que n <= 10.

D- On continue de la boucle while tant que n > 10.

E- On continue de la boucle while tant que n < 10.

F- On continue de la boucle while tant que n <= 10.

On reprend l'exercice qui permettait de savoir si un nombre entier $n$ fait partie d'une liste lst ou non. ( lien vers l'exercice similaire traité avec la boucle for.)

  1. En utilisant une boucle while, écrire une fonction est_dans_liste2 qui prend en paramètres une liste lst et un entier n et qui renvoie True si l'entier est dans la liste et False sinon.

    1. Vous pouvez utiliser l'instruction len qui renvoie la taille d'une liste donnée en paramètre.

      Exemple : len([1,4,6,5,8,3]) renvoie 6 car 6 termes composent la liste.

    2. Attention ! Les éléments d'une liste sont référencés à partie de 0 et non de 1.

      Exemple : Si lst = [10,4,6,5,8,3], lst[0] renvoie 10 car 10 est le premier terme de la liste.
      lst[1] renvoie 4 car 4 est le deuxième terme de la liste.

  2. Tester la fonction est_dans_liste2, entre autres, est_dans_liste2([8,4,7,2,5,4],6) renvoie False et est_dans_liste2([8,4,7,2,5,4],4) renvoie True.

  3. On considère dans cette question d'une liste de taille importante.

    À votre avis les fonctions est_dans_liste, écrite avec un for, et est_dans_liste2, écrite avec un while ont-elles un coût en temps d'exécution proche ou l'une des deux, en général, pourrait être plus rapide à renvoyer un résultat ?

Vous allez programmer un jeu de nombre à deviner contre un ordinateur. Pour commencer l'ordinateur va choisir au hasard un nombre compris entre 1 et 100.

Ensuite, l'utilisateur doit alors deviner ce nombre comme ceci :

  1. Rappeler les lignes de codes à écrire en Python afin d'obtenir un nombre entier entre 1 et 100.

  2. Écrire une procédure plus_ou_moins, sans paramètre d'entrée ni retour qui correspond au jeu du nombre à deviner.

    Voici un exemple de traces d'affichages successifs obtenus sur un jupyter-notebook dans le cas où l'ordinateur avez choisi au hasard le nombre 41 : 

    Donnez un entier entre 1 et 100. 50
La réponse est inférieure à votre propositon. Essayez encore !25
La réponse est supérieure à votre propositon. Essayez encore !32
La réponse est supérieure à votre propositon. Essayez encore !41
Bravo ! Vous avez gagné !

  3. On veut complexifier le jeu en imposant un nombre d'essais maximal.

    Modifier la fonction précédente en une nouvelle plus_ou_moins2 qui :

    • prend un nombre entier comme paramètre, nombre entier qui corrrespond au nombre maximum d'essais autorisés,

    • permet de jouer comme précédent sans permettre plus d'essais que le nombre maximum entré,

    • affiche soit la défaite soit la victoire en précisant le nombre d'essais nécessaires.

  4. Proposer des préconditions à cette fonction plus_ou_moins2.

Ayant travaillé durant les grandes vacances dernières, vous avez un pécule de 500€. Vous décidez de placer cet argent en banque.

La banque vous propose un compte rémunéré à 1% par an, c'est-à-dire que chaque fin d'année vous recevez 1% d'intérêt sur la somme présente sur le compte en début d'année.

Vous aimeriez savoir quand vous aurez sur votre compte 700€.

Proposez une fonction, sans paramètre, qui renvoie le nombre d'années d'attente nécessaires pour avoir 700€ sur le compte.

exercice de renforcement

Lorsque l'utilisateur saisit une donnée, il peut être utile de vérifier qu'elle est conforme à ce qu'on attend de lui.

  1. Proposer un programme qui demande à l'utilisateur de rentrer un nombre positif.

  2. Compléter ce programme afin de demander à l'utilisateur de saisir un nouveau nombre si le nombre entré ne correspond pas à la demande.

  3. Modifier le programme précédent pour limiter la répétition à au plus 10 demandes successives.
    Rajouter un message d'arrêt si l'utilisateur "s'obstine" à saisir un nombre strictement négatif.

Votre enseignant vous exploite : il vous demande de créer un programme qui lui renverra la moyenne des notes saisies.

Pour cela, il vous donne le cahier des charges suivant :

  1. Proposer une fonction continuer qui répond au cahier des charges. Faire en sorte que la casse (=minuscule ou majuscule) ne soit pas un problème pour la saisie, par exemple en utilisant ma méthode upper.

    "mélanGes".upper() renvoie 'MÉLANGES'.

  2. Tester la fonction continuer créée.

  3. Proposer une fonction moyenne qui répond au cahier des charges. Cette fonction aura trois paramètres :

    • moy un flottant qui correspond à la moyenne pour l'instant obtenue,
    • nb_notes un entier qui correspond au nombre de notes déjà pris en compte dans la moyenne moy,
    • new_note un flottant qui correspond à la nouvelle note à prendre en compte pour la moyenne.

    Cette fonction renverra la moyenne de l'ensemble des notes saisies (en comptant aussi la dernière).

    Aide mathématique :

    On considère deux ensembles de notes A et B de moyenne respective $moy_A$ et $moy_B$ comprenant respectivement $nb_A$ et $nb_B$ notes. La moyenne des notes formant la réunion de ces deux ensembles est doné par la formule :

    $$ moyenne = \frac{moy_A \times nb_A + moy_B \times nb_B}{nb_A + nb_B}$$.

  4. Tester la fonction moyenne créée.

  5. Proposer une fonction main qui répond au cahier des charges. Cette fonction fera appel aux deux fonctions continuer et moyenne et n'aura pas de paramètre ; elle renverra la moyenne de toutes les notes successivement saisies.

  6. Tester votre programme principal, par exemple en saisissant successivement les valeurs 10, 19 et 13.

Vous avez décider de partir en randonnée avec un ami. Celui possède un très grand sac pesant 5.2kg et a une technique très particulière pour le remplir : il prend au hasard des éléments parmi tout le nécessaire à emporter et s'arrête dès que le poids obtenu dépasse 20 kg. Les objets choisis au hasard pèsent tous entre 10 et 500 grammes.

Comme vous êtes très intrigué.e par sa manière de faire, vous décider de modéliser la situation informatiquement afin d'évaluer en moyenne combien d'éléments va prendre votre ami dans son sac.

Pour cela, vous disposez des informations suivantes :

  1. Proposer une fonction remplir_sac, sans paramètre, qui renvoie la liste des masses des objets du sac de sorte que le remplissage s'arrête dès que la masse totale dépasse 20 kg.

  2. Proposer une fonction nb_objets qui prend en paramètres une liste et renvoie le nombre d'éléments de cette liste.

  3. Proposer une fonction qui renvoie une moyenne du nombre d'éléments que va prendre cet ami dans son sac.

Écrire une fonction triangle qui prend en paramètre un nombre entier n et qui affiche un triangle isocèle formé d’étoiles.
La hauteur du triangle (c’est-à-dire le nombre de lignes) correspond à l'argument n, comme dans l’exemple ci-dessous.
On s’arrangera pour que la dernière ligne du triangle s’affiche sur le bord gauche de l’écran.
Exemple d'exécution de triangle(6) : 


     *
    ***
   *****
  *******
 *********
***********

Écrire un code qui affiche toutes les manières possibles d’obtenir un euro avec des pièces de 2 cents, 5 cents et 10 cents. Faire aussi afficher combien de possibilités ont été ainsi trouvées.

Les résultats seront affichés comme suit :


1 euro = 50 X 2c
1 euro = 45 X 2c 2 X 5c
1 euro = 40 X 2c 4 X 5c
1 euro = 35 X 2c 6 X 5c
1 euro = 30 X 2c 8 X 5c
1 euro = 25 X 2c 10 X 5c
1 euro = 20 X 2c 12 X 5c
1 euro = 15 X 2c 14 X 5c
1 euro = 10 X 2c 16 X 5c
1 euro = 5 X 2c 18 X 5c
1 euro = 20 X 5c
1 euro = 45 X 2c 1 X 10c
1 euro = 40 X 2c 2 X 5c 1 X 10c
1 euro = 35 X 2c 4 X 5c 1 X 10c
1 euro = 10 X 2c 2 X 5c 7 X 10c
1 euro = 5 X 2c 4 X 5c 7 X 10c
1 euro = 6 X 5c 7 X 10c
1 euro = 10 X 2c 8 X 10c
1 euro = 5 X 2c 2 X 5c 8 X 10c
1 euro = 4 X 5c 8 X 10c
1 euro = 5 X 2c 9 X 10c
1 euro = 2 X 5c 9 X 10c
1 euro = 10 X 10c
En tout, il y a 66 façons de faire 1 euro

Écrire un algorithme qui affiche la « table de multiplication » des nombres de 1 à 10, sous la forme suivante : 


     | 01  02  03  04  05  06  07  08  09  10 
 --------------------------------------------
01   | 01  02  03  04  05  06  07  08  09  10 
02   | 02  04  06  08  10  12  14  16  18  20 
03   | 03  06  09  12  15  18  21  24  27  30 
04   | 04  08  12  16  20  24  28  32  36  40 
05   | 05  10  15  20  25  30  35  40  45  50 
06   | 06  12  18  24  30  36  42  48  54  60 
07   | 07  14  21  28  35  42  49  56  63  70 
08   | 08  16  24  32  40  48  56  64  72  80 
09   | 09  18  27  36  45  54  63  72  81  90 
10   | 10  20  30  40  50  60  70  80  90  100

Pour gérer l'affichage des nombres et faire en sorte que les premiers s'écrivent avec deux chiffres, vous pouvez utiliser le symbole % :

  • le signe % suivi d’une lettre indiquant le type de la variable :

    • %s : chaîne de caractères ;

    • %d : nombre entier ;

    • %.Xd : X désignant un nombre entier indiquant le nombre de chiffres minimal pour écrire le nombre entier ;

    • %f : nombre décimal ;

    • %.Xf : X désignant un nombre entier indiquant le nombre de décimales après la virgule.

  • Le signe % derrière l'apostrophe de fermeture introduit la valeur de chaque variable (dans l’ordre d’apparition respectif dans le texte, un peu comme la méthode format() )

  • print('%d'%1234) renvoie 1234 ;

  • print('%.2d'%1234) renvoie 1234 ;

  • print('%.6d'%1234) renvoie 001234 ;

  • print("valeur1=%.6d , valeur2=%.3f" %(1234,1.23456)) renvoie valeur1=001234 , valeur2=1.235.

Le parcours France IOI

Vous pouvez vous rendre sur le site France IOI. Créer un compte et rejoindre le groupe NSI de votre lycée.

Il faut attendre qu'un professeur valide votre compte.

Nous pouvons visualiser votre progression. Ce travail sera valorisé.

Il est idéal si vous avez des difficultés avec l'algorithmique mais idéal aussi pour vous perfectionner.

Exercices de renforcement

Sur la boucle for avec range

Écrire une fonction produit qui prend comme paramètre un entier naturel $n$ et renvoit le produit de tous les nombres entiers compris entre 1 et $n$.

Exemple : pour produit(4) renvoie 24 car $P=1\times 2\times 3\times 4=24$.

Pour accéder au code de la correction : lien

Vous travaillez pour un magasin de bricolage.

Vous avez à gérer un programme informatique qui créé l'affichage du prix à payer suivant le nombre de vis particulières.

Chaque vis coûte 0.15€.

Écrire une procédure prix_visqui reçoit en entrée un nombre entier $n$ et affiche en sortie un ensemble de lignes ; chaque ligne affiche le prix à payer pour un nombre de vis.

Par exemple, prix_vis(10) conduit à l'affichage suivant (la partie centrale n'a pas été reproduite) :

Remarquez que le calcul avec des flottants est imprécis. On pourrait utiliser la fonction round par exemple pour arrondir au centime d'euro.

Pour accéder au code de la correction : lien

Vous travaillez pour une ONG qui creuse des puits en zone sahélienne.

Il y a un coût fixe de 800€ pour l'étude de chantier et l'apport du matériel sur la zone.

Le premier mètre coûte 50€ pour être creusé.

Chaque mètre supplémentaire creusé coûte 5€ de plus que le précédent.

Par exemple, le deuxième mètre creusé coûte 55€, le troisième 60€, ...
Ainsi, le coût total pour creuser un puits de trois mètres de profondeur est de 800+50+55+60=965 €.

Écrire une fonction cout_puits qui en entrée reçoit un entier $n$ non nul qui corespond à la profondeur en mètres du puits à percer et en sortie renvoie le côut total de percement en euros.

Une fois la fonction écrite, rajouter une ou des préconditions afin que $n$ soit bien un entier non nul.

Pour accéder au code de la correction : lien

for avec un itérable

  1. Écrire une fonction occurence_dans_liste qui prend en paramètre une liste lst et un entier $n$ et qui renvoie le nombre de fois où l'entier $n$ apparaît dans la liste.

  2. Tester la fonction occurence_dans_liste, entre autres, occurence_dans_liste([8,4,7,2,5,4],6) renvoie 0 et occurence_dans_liste([8,4,7,2,5,4],4) renvoie 2.

  3. Proposer au moins trois tests pour valider cette fonction.

Pour accéder au code de la correction : lien

La boucle répétitive conditionnelle while

  1. Écrire une fonction produit2, utilisant une boucle while qui prend comme paramètre un entier naturel $n$ et renvoit le produit de tous les nombres entiers compris entre 1 et $n$.

    Exemple : pour produit2(4) renvoie 24 car $P=1\times 2\times 3\times 4=24$.

  2. Proposer au moins deux tests pour valider cette fonction.

  3. Rajouter une précondition sur $n$ pour s'assurer que $n$ est bien un entier naturel non nul.

Pour accéder au code de la correction : lien

Karamoko place 1200€ sur un compte rémunéré à 1.3%, c'est-à-dire que chaque fin d'année la banque rajoute au capital placé par Karamoko 1.3% d'intérêt par rapport à la somme présente sur le compte en début d'annnée.

  1. Écrire une fonction attendre qui prend comme paramètre d'entrée un flottant objectif indiquant la somme qu'aimerait atteindre Karamoko sur son compte et renvoie un entier indiquant le nombre d'annéess nécessaire pour atteindre cette somme.

  2. Proposer une précondition à cette fonction.

  3. Comme l'espérance de vie d'une personne plaçant de l'argent en banque est inférieure à 100 ans, rajouter une postcondition à cette fonction.

Pour accéder au code de la correction : lien

Chaque année la consommation énergétique d'un data center est estimée augmenter de 8 %.
Déterminer le nombre d'années nécessaires au doublement de la consommation énegétique de ce data center.

Le résultat ne dépend pas de la consommation énergétique actuelle de ce data center.

Pour accéder au code de la correction : lien

Des mini-projets en Python

Dès que vous avez terminé ce parcours "de base" vous devez vous lancer dans des mini-projets.

Vous devez vous mettre par groupe de trois

Votre projet doit être achevé au retour des vacances le 4 novembre

Ce projet sera présenté à vos professeurs selon une organisation que l'on fixera.

La forme de ce projet est laissé libre, il faut rendre un support qui décrit votre projet et qui contient des codes pythons.

Chacun doit être capable de décrire sa participation dans le groupe.

Le choix du projet est libre, ne soyez pas torp ambitieux, vous débutez.

Vous pouvez partir sur des projets existants

Il faudra être capable d'expliquer les codes pythons et de montrer les modifications que vous avez apporté.

Pensez bien à documenter et à tester vos fonctions et programmes en laissant apparentes les préconditions et les postconditions utilisées.

Quelques idées :


Pour un projet, il faudra être capable de faire une explication rapide de votre idée et d'organiser une démo (fonction utilisateur) à vos professeurs.

QCM

Questions issues de la Banque Nationale de Sujets

Propriétaire des ressources ci-dessous : ministère de l'Éducation nationale et de la jeunesse, licence CC BY SA NC

Voici une sélection de questions issues de la banque nationale de sujets, répondez à ces questions (attention, cette sélection n'est pas exhaustive).

Quelle est la valeur du couple $(s,i)$ à la fin de l'exécution du script suivant ? 

s = 0
i = 1
while i < 5:
    s = s + i
    i = i + 1

Réponses :

A- (4,5)

B- (10,4)

C- (10,5)

D- (15,5)

$𝑛$ étant un entier strictement positif, la fonction suivante calcule sa factorielle, c'est-à-dire le produit $1 \times 2 \times 3 \times ⋯ \times (𝑛 − 1) \times 𝑛$. Comment faut-il écrire la ligne en pointillée ci-dessous pour ce faire ? 

def factorielle(n):
    f = 1
    .........
        f = f * i
    return f

Réponses :

A- for i in range(1,n):

B- for i in range(n+1):

C- for i in range(0,n):

D- for i in range(1,n+1):

On exécute le script suivant : 

a = 4
b = 4
c = 4
while a < 5:
    a = a - 1
    b = b + 1
    c = c * b

Que peut-on dire ?

Réponses :

A- ce programme ne termine pas

B- à la fin de l'exécution, la variable a vaut 5

C- à la fin de l'exécution, la variable b vaut 34

D- à la fin de l'exécution, la variable c vaut 42

On souhaite écrire une fonction qui renvoie le maximum d'une liste d'entiers : 

def maximum(L):
    m = L[0]
    for i in range(1,len(L)):
        if .........:
            m = L[i]
    return m

Par quoi faut-il remplacer les pointillés pour que cette fonction produise bien le résultat attendu ?

Réponses :

A- i > m

B- L[i] > m

C- L[i] > L[i-1]

D- L[i] > L[i+1]

Quelle est la valeur de c à la fin de l'exécution du code suivant : 

L = [1,2,3,4,1,2,3,4,0,2]
c = 0
for k in L:
    if k == L[1]:
        c = c+1

Réponses :

A- 0

B- 2

C- 3

D- 10

Que renvoie la fonction suivante quand on l'appelle avec un nombre entier et une liste d'entiers ? 

def mystere(n,L):
    for x in L:
        if n == x:
            return True
    return False

Réponses :

A- une valeur booléenne indiquant si le nombre n est présent au moins une fois dans la liste L

B- une valeur booléenne indiquant si le nombre n est présent plusieurs fois dans la liste L

C- une valeur booléenne indiquant si le nombre n est le plus grand de la liste L

D- une valeur booléenne indiquant si le nombre n est le plus petit de la liste L

La fonction mystere suivante prend en argument un tableau d'entiers. 

def mystere(t):
    for i in range(len(t) - 1):
        if t[i] + 1 != t[i+1]:
            return False
    return True

À quelle condition la valeur renvoyée par la fonction est-elle True ?

Réponses :

A- si le tableau passé en argument est une suite d'entiers consécutifs

B- si le tableau passé en argument est trié en ordre croissant

C- si le tableau passé en argument est trié en ordre décroissant

D- si le tableau passé en argument contient des entiers tous identiques

T est un tableau de nombres entiers non vide. Que représente la valeur de s renvoyée par cette fonction ? 

def mystere(T):
    s = 0
    for k in T:
        if k % 2 == 0:
            s = s+k
    return s

Réponses :

A- la somme des valeurs du tableau T

B- la somme des valeurs positives du tableau T

C- la somme des valeurs impaires du tableau T

D- la somme des valeurs paires du tableau T

On considère le code incomplet suivant qui recherche le maximum dans une liste. 

liste = [5,12,15,3,15,17,29,1]
iMax = 0
for i in range(1,len(liste)):
    ............
    iMax = i
print (liste[iMax])

Par quoi faut-il remplacer la ligne pointillée ?

Réponses :

A- if i > iMax:

B- if liste[i] > liste[iMax]:

C- if liste[i] > iMax:

D- if i > liste[iMax]:

Quelle est la valeur de element à la fin de l'exécution du code suivant : 

L = [1,2,3,4,1,2,3,4,0,2]
element = L[0]
for k in L:
    if k > element:
element = k

Réponses :

A- 0

B- 1

C- 4

D- 10

La fonction suivante doit calculer la moyenne d’un tableau de nombres, passé en paramètre. Avec quelles expressions faut-il remplacer les points de suspension pour que la fonction soit correcte ? 

def moyenne(tableau):
    total = ...
    for valeur in tableau:
        total = total + valeur
    return total / ...

Réponses :

A- 1 et (len(tableau) + 1)

B- 1 et len(tableau)

C- 0 et (len(tableau) + 1)

D- 0 et len(tableau)

Quelle est la valeur de la variable n à la fin de l'exécution du script ci-dessous ? 

n = 1
while n != 20:
    n = n + 2

Réponses :

A- 1

B- 20

C- 22

D- le programme ne termine pas, la boucle tourne indéfiniment

Soit 𝑛 un entier naturel. Sa factorielle est le produit des nombres entiers strictement positifs qui sont plus petits ou égaux à 𝑛. Par exemple la factorielle de 4 vaut 1 × 2 × 3 × 4 = 24. Quelle est la fonction correcte parmi les suivantes ?

Réponses :

A- 

def factorielle(n):
    i = 0
    fact = 1
    while i <= n:
        fact = fact * i
        i = i + 1
    return fact

B- 

def factorielle(n):
    i = 1
    fact = 1
    while i < n:
        fact = fact * i
        i = i + 1
    return fact

C- 

def factorielle(n):
    i = 0
    fact = 1
    while i < n:
        i = i + 1
        fact = fact * i
    return fact

D- 

def factorielle(n):
    i = 0
    fact = 1
    while i <= n:
        i = i + 1
        fact = fact * i
    return fact

On exécute le script suivant : 

for i in range(n):
    for j in range(i):
        print('NSI')

Combien de fois le mot NSI est-il affiché ?

Réponses :

A- $n^2$

B- $(n+1)^2$

C- $1+2+...+(n-1)$

D- $1+2+...+(n-1)+n$

La fonction suivante doit calculer le produit de tous les éléments de la liste passée en paramètre. Avec quelles expressions doit-on la compléter pour que cette fonction soit correcte ? 

def produit (L):
    p = ...
    for elt in L:
        .......
    return p

Réponses :

A- 1 puis p = p * elt

B- 0 puis p = p * elt

C- 1 puis p = elt

D- 0 puis p = elt

On considère un entier positif $A$.
Parmi les quatre codes suivants, il y en a un dont l'exécution ne termine pas. Lequel ?

Réponses :

A- 

i = A + 1
while i < A:
    i = i - 1

B- 

i = A + 1
while i < A:
    i = i + 1

C- 

i = A - 1
while i < A:
    i = i - 1

D- 

i = A - 1
while i < A:
    i = i + 1

Que peut-on dire du programme Python suivant de calcul sur les nombres flottants ? 

x = 1.0
while x != 0.0:
    x = x - 0.1

Réponses :

A- l'exécution peut ne pas s'arrêter, si la variable x n'est jamais exactement égale à 0.0

B- à la fin de l'exécution, x vaut – 0.00001

C- à la fin de l'exécution, x vaut 0.00001

D- l'exécution s'arrête sur une erreur FloatingPointError

Soit T un tableau de flottants, a et b deux entiers. On considère une fonction nommée somme renvoyant la somme des éléments du tableau d'indice compris entre a et b définie par : 

def somme(T, a, b):
    S = 0
    for i in range(a, b+1) :
        S = S + T[i]
    return S

Quel ensemble de préconditions doit-on prévoir pour cette fonction ?

Réponses :

A- a < b

B- a < longueur(T) et b < longueur(T)

C- a <=b < longueur(T)

D- a <=b < longueur(T) et T est un tableau trié

Autres QCM

Les QCM suivants sont issus de https://genumsi.inria.fr.

(Auteur Nicolas Revéret)

On souhaite que l’utilisateur saisisse une valeur entière comprise entre 1 et 20 (inclus).
Quel code est correct ?

Réponses :

A- 

a = int ( input("Saisir un nombre entre 1 et 20") )
while (a < 1 and a > 20) :
    a = int ( input("Saisir un nombre entre 1 et 20") )

B- 

while (a < 1 and a > 20) :
    a = int ( input("Saisir un nombre entre 1 et 20") )

C- 

a = int ( input("Saisir un nombre entre 1 et 20") )
while (a < 1 or a > 20) :
    a = int ( input("Saisir un nombre entre 1 et 20") )

D- 

a = int ( input("Saisir un nombre entre 1 et 20") )
while (a >=1 and a >= 20) :
    a = int ( input("Saisir un nombre entre 1 et 20") )

(Auteur Nicolas Revéret)

On souhaite écrire un programme affichant tous les entiers multiples de 3 entre 6 et 288 inclus.
Quel code est correct ?

Réponses :

A- 

for n in range(6, 288, 3) :
    print(n)

B- 

for n in range(6, 289) :
    print(n/3)

C- 

for n in range(6, 288) :
    print(3 * n)

D- 

for n in range(6, 290, 3) :
    print(n)

(Auteur : Sylvie Genre)

$a$ et $m$ étant des entiers strictement positifs,la fonction suivante calcule $a^m$ : 

def puissance (a,m) :
    p = 1
    n = 0
    while n < m :
        p = p * a
         #
        n = n + 1
    return p

À la ligne marquée d'un #, on a, après le # :

Réponses :

A- $p = a^n$

B- $p = a^{n+1}$

C- $p = a^{n-1}$

D- $p = a^{m}$

Sitographie

Savoir faire et Savoir

Licence Creative Commons
NSI de Auteurs : Jean-Christophe Gérard, Thomas Lourdet, Johan Monteillet, Pascal Thérèse est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.
▲