L'algorithme de Boyer-Moore est un algorithme de recherche de sous-chaîne particulièrement efficace. Il a été développé par Robert S. Boyer et J Strother Moore en 1977.

Dans ce chapitre nous traitons un algorithme qui s'approche de celui de Boyer Moore sans l'atteindre réellement.

Cours réalisé à partir du document d'accompagnement sur cette partie du programme

Problématique

L'objectif de ce cours est de réfléchir à la recherche de motifs dans une chaîne de caractères.

Autrement dit, il s'agit d'écrire des scripts qui permettent de vérifier qu'un motif (=mot, chaîne de caractères etc) se trouve à l'intérieur d'une chaîne de caractères.

Quelques notations et structures pour mettre en place l'algorithme.

Dans toute la suite on cherche la première occurrence d’un motif ( = chaîne de caractère) d'une longueur donnée dans un texte.

Définissons et nommons les variables qui vont nous être utile à l'écriture de l'algorithme:

Au cours de la recherche, on pose une fenêtre de taille long sur le texte, sur laquelle on aligne le motif.

On notera position la variable contenant l'index du caractère de texte qui est en face du premier élément de la fenêtre.

Enfin, nous notons j la variable contenant l'index du caractère du motif à comparer à un caractère du texte.

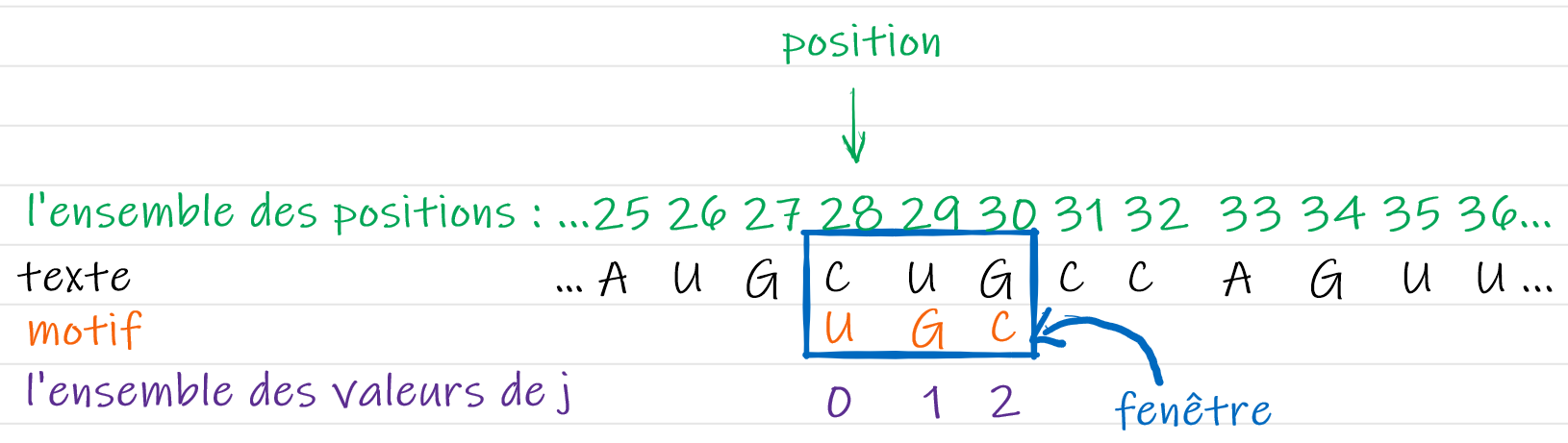
S'il n’y a pas correspondance entre le motif et la partie du texte que la fenêtre éclaire, on décalera la fenêtre avant de recommencer la comparaison.

Dans tous les algorithmes présentés ici, la fenêtre se déplacera toujours de gauche à droite.

Déterminer la longueur du texte, la valeur de position, les valeurs possibles pour j et la valeur de long dans l'image suivante :

Code de déblocage de la correction :

Même exercice avec l'image:

Code de déblocage de la correction :

Avec les notations de la définition précédente, quel est le script qui permettra de comparer le caractère d'indice j dans le motif avec le caractère qui lui fait face dans le texte?

Code de déblocage de la correction :

À quelle condition pourrons nous faire glisser la fenêtre de comparaison sur le texte ?
Écrire la réponse avec les notations précédentes.

Code de déblocage de la correction :

L'algorithme Naïf

Écartons immédiatement l'usage du in de Python, qui renvoie simplement un booleen sans nous renseigner sur la position du motif ou bien le nombre d'occurrences.

De plus, ce cours est un cours d'algorithme et le in est une facilité de Python qui peux nous éloigner de la comprehension complète de l'algorithme.

L’algorithme naïf consiste simplement à comparer un à un, de gauche à droite, les caractères du texte apparaissant dans la fenêtre avec ceux du motif. En cas de non-correspondance, on avance simplement la fenêtre d’une unité vers la droite.

Dans cet exercice, on veut écrire une fonction qui nous informe sur la correspondance du motif sur la partie du texte éclairée par la fenêtre ainsi que le décalage à appliquer.

  1. Écrire une fonction idem(texte, motif, position, long) qui renvoie un tuple constitué :

    • d'un booléen True si le motif de longueur long se trouve dans le chaîne de caractères texte à l'index position et False sinon.

    • d'un entier correspondant au décalage à appliquer : 1 si on n'a pas correspondance et 0 sinon.

    Par exemple, idem("veni vidi vici", "vi", 3, 2) renvoie le tuple (False, 1), mais idem("veni vidi vici", "vi", 10, 2) renvoie le tuple (True, 0).

    Code de déblocage de la correction :

  2. Écrire une fonction rechercher(texte, motif) qui renvoie l'indice du premier caractère du motif dans le texte s'il est présent et -1 sinon. On utilisera la fonction idem précédente.

    Par exemple rechercher("veni vidi vici", "vi") renvoie l'indice 5

Code de déblocage de la correction :

Le script suivant permet de charger le fichier text.txt: 

fichier = open('text.txt', 'r')
texte = fichier.read()
fichier.close()

  1. Télécharger Le soleil est toujours riant-Racine et Le Rouge et le noir.-Stendhal puis tester votre fonction rechercher précédente avec le motif "tel".

  2. Qu'observez vous?

Code de déblocage de la correction :

Proposer au moins une précondition à la fonction rechercher

Code de déblocage de la correction :

Algorithme d'Horspool vers Boyer-Moore

Principe général

Nigel Horspool est né en Grande-Bretagne mais citoyen canadien. Il est professeur émérite d’informatique de l’université de Victoria, retraité depuis 2016. Il a conçu l'algorithme que nous décrivons maintenant.

On décale toujours la fenêtre de gauche à droite.

Déroulement de l'algorithme

Nous considérons ici la recherche du motif 'mai' dans le texte "lesmathsatapmaislinfoctopossi".

Avec nos notations, long=3, n=29 et la première occurrence du motif dans le texte apparaît en position 12.

On commence avec la fenêtre tout à gauche, c’est-à-dire avec position=0.

lesmathsatapmaislinfoctopossi
mai

Comme on commence à comparer de droite à gauche, c’est pour j=2 qu’il y a non-correspondance : motif[j]!= texte[position + j], en effet motif[j]=motif[2]='i' et texte[position+j]=texte[0+2]='s'.

Le caractère texte[position+j]=texte[0+2]='s' n'apparait pas dans le motif, on peut donc décaler de la longeur du motif ici 3 :

lesmathsatapmaislinfoctopossi
   mai

On commence à comparer de droite à gauche, c’est pour j=2 qu’il y a non-correspondance : motif[j]!= texte[position + j], en effet motif[j]=motif[2]='i' et texte[position+j]=texte[3+2]='t'.

Là encore le caractère texte[position+j]=texte[0+2]='t' n'apparait pas dans le motif, on peut donc décaler de la longeur du motif ici 3 :

lesmathsatapmaislinfoctopossi
      mai

On commence à comparer de droite à gauche, c’est pour j=2 qu’il y a non-correspondance : motif[j]!= texte[position + j], en effet motif[j]=motif[2]='i' et texte[position+j]=texte[6+2]='a'.

Mais cette fois, le caractère texte[j+position]=texte[2+6]='a' apparait dans le motif, on peut donc opérer un decalage de 1 pour mettre en face les caractères identiques ici 'a' :

lesmathsatapmaislinfoctopossi
       mai

On commence à comparer de droite à gauche, c’est pour j=2 qu’il y a non-correspondance : motif[j]!= texte[position + j], en effet motif[j]=motif[2]='i' et texte[position+j]=texte[7+2]='t'.

Cette fois le caractère texte[position+j]=texte[0+2]='t' n'apparaît pas dans le motif, on peut donc décaler de la longeur du motif ici 3 :

lesmathsatapmaislinfoctopossi
          mai

On commence à comparer de droite à gauche, c’est pour j=2 qu’il y a non-correspondance : motif[j]!= texte[position + j], en effet motif[j]=motif[2]='i' et texte[position+j]=texte[10+2]='m'.

Cette fois le caractère texte[position+j]=texte[0+2]='m' apparaît dans le motif à la position 0 du motif, on peut donc décaler de la longeur du motif ici 2 pour mettre en face les caractères identiques ici 'm' :

lesmathsatapmaislinfoctopossi
            mai

Cette fois il y a correspondance et la position de la première occurrence du motif est 12.

Calcul du décalage.

  1. Dans le cas où le caractère du texte texte[position+j] ne correspond pas au caractère motif[j] et qu'il n’apparaît pas du tout dans le motif, il convient d'opérer un décalage de j+1.

  2. Dans le cas où le caractère du texte texte[position+j] ne correspond pas au caractère motif[j] et qu'il apparaît dans le motif : en notant r la position la plus à droite de ce caractère dans le motif, il convient d'opérer un décalage de j-r.

Le '+1' de la formule du décalage dans le cas où le caractère est absent du motif vient du fait que j est un index de position : la première position correspond à 0 et non à 1.

Déterminer les décalages à appliquer dans les cas suivants :

  1. jadorecetexerciceetlavie
    cete
  2. jadorecetexerciceetlavie
       cete
  3. jadorecetexerciceetlavie
               cete

Code de déblocage de la correction :

prétraitement du motif

Écrire une fonction pretraitement_motif(motif, long) qui renvoie un dictionnaire dont les clés sont les caractères de la chaîne de caractères motif et les valeurs l'index de la dernière occurence de la clé dans cette chaîne de caractères.

Code de déblocage de la correction :

Écrire une fonction droite(caractere,motif,long) qui renvoie la position la plus à droite du caractère dans le motif de longueur long si le caractère appartient à motif et -1 sinon. Vous utiliserez la fonction précédente.

Code de déblocage de la correction :

Ce sont ces fonctions que nous allons utiliser pour réaliser le calcul de décalage. Le dictionnaire renvoyé par pretraitement_motif est le même lors de l'ensemble de l'algorithme de recherche de motif. Il est indépendant du texte observé.

L'usage d'une variable globale pour ce dictionnaire dico_pre est justifié. Cela permettra de l'utiliser à chaque appel de fonction sans devoir le reconstuire.

Variable globale en Python

Cette partie est là pour ceux qui ne se sentent pas à l'aise avec les variables globales.

Une variable globale est une variable qui reste en mémoire du moment qu'elle a été implémentée et tant que le noyau Python fonctionne.

Pour déclarer une variable globale x on utilisera le script : 

global x

Pour lui donner une valeur on procédera comme pour une variable locale : 

x = 0

global a,b
a=4
b=6
def f(x):
    return a*x+b
print(f(5))

  1. Tester le script précédent.

  2. Tester le script précédent sans la première ligne.

Prétraitement avec un variable globale

Refaire les fonctions pretraitement_motif et droite mais cette fois le dictionnaire pre doit être une variable globale.

Code de déblocage de la correction :

idem version décalage

Écrire une fonction idem2(texte, motif, position, long) qui renvoie un tuple constitué :

Code de déblocage de la correction :

Algorithme de Horspool

Ecrire la fonction rechercher qui utilise l'algorithme de Horspool.

Code de déblocage de la correction :

Nous n'irons pas jusqu'à l'algorithe de Boyer Moore qui est plus compliqué encore que celui de Horspool.

Réaliser la même fonction mais sans variable globale.

Code de déblocage de la correction :

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲