Demandez le programme !

Quelques repères historiques de la calculabilité

Quelques vidéos pour votre culture :

Alan Turing (1912-1954), sa vie en quelques minutes.

Vous pouvez également visionner le film "imitation game". Synopsis officiel du film : "En 1939, alors que la guerre débute, Turing, déjà reconnu pour ses talents de mathématicien, se rend à Bletchley Park et rejoint l'équipe de cryptographie, sous les ordres du commandant Alastair Denniston. Il est accompagné par le maître d'échecs Hugh Alexander, John Cairncross, Peter Hilton, Keith Furman et Charles Richards. Cette équipe va alors tenter de décrypter la machine de cryptographie utilisée par les nazis : Enigma."

Ce travail secret ne sera connu du public que dans les années 1970. Après la guerre, il travaille sur un des tout premiers ordinateurs, puis contribue au débat sur la possibilité de l'intelligence artificielle, en proposant le test de Turing. Vers la fin de sa vie, il s'intéresse à des modèles de morphogenèse du vivant conduisant aux « structures de Turing ». Poursuivi en justice en 1952 pour homosexualité, il choisit, pour éviter la prison, la castration chimique par prise d'œstrogènes. Il est retrouvé mort par empoisonnement au cyanure le 8 juin 1954 dans la chambre de sa maison à Wilmslow (une pomme croquée posée sur sa table de nuit). La reine Élisabeth II le reconnaît comme héros de guerre et le gracie à titre posthume en 2013.

La pomme croquée d'une célèbre marque est un hommage à ce brillant mathématicien.

Pour les curieux : le coin des machines à calculer mécaniques.

Quelques vidéos :

La machine de Turing

Attention cette section 2 sur la machine de Turing hautement culturelle n'est pas un attendu du programme de terminale NSI. Elle peut néanmoins servir de support à un projet.

En 2012 Alan Turing aurait fêté son 100 ième anniversaire. À cette occasion, des universitaires ont construit une machine de Turing en LEGO.

Accès au site

Une machine de Turing est un appareil théorique disposant :

Le fonctionnement de la machine atteint (ou pas) un état particulier qui provoque son arrêt. Cet état particulier est souvent appelé état final.

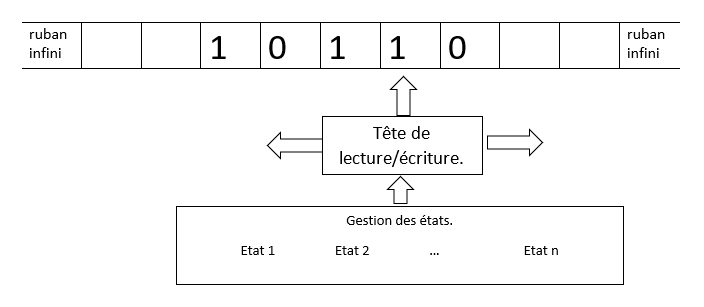
texte de remplacement

Pour représenter l'ensemble des états, on peut utiliser une table des transitions.

Elle permet de définir, pour chaque état, selon le résultat de la lecture, les actions à exécuter : écriture, déplacement, choix d'un nouvel état.

Pour écrire cette table, il faut :

Dans certains exercices, on déplace le ruban mais pas la tête de lecture/écriture.

Alphabet : {'0', '1', 'b'}, 'b' pour un "blanc", c'est-à-dire une case du ruban sans "0" ni "1".

Etat Lit Ecrit Déplace Suivant
e0 blanc rien droite e0

À l'état e0 si la tête lit un blanc, elle n'écrit rien, se déplace à droite et reste à l'état e0

Cette table des transitions donnait naissance à une carte percée de trous que l'on pouvait insérer dans la machine. À l'aide d'aiguilles et de relais électro-mécaniques, ces informations provoquaient des actions dans la machine. Ces cartes étaient les programmes de la machine. Par contre Alan Turing ne verra pas sa "machine" fonctionner.

On peut construire un diagramme de la machine (on parle aussi d' automate).

Pour définir un diagramme, il faut :

Alphabet : {'0', '1', 'b'}

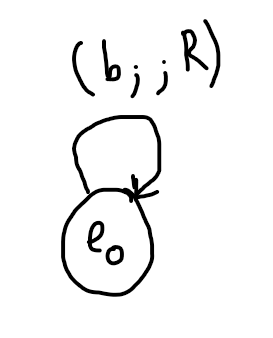texte de remplacement À l'état e0, si la tête lit un blanc alors elle n'écrit rien et se déplace à droite en restant à l'état e0.

Alphabet : {'0', '1', 'b'}

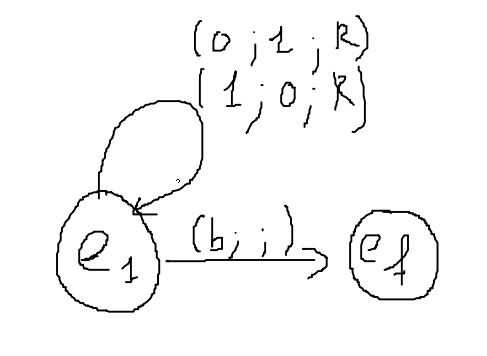
texte de remplacement

Alphabet : {'0';'1;'b'}

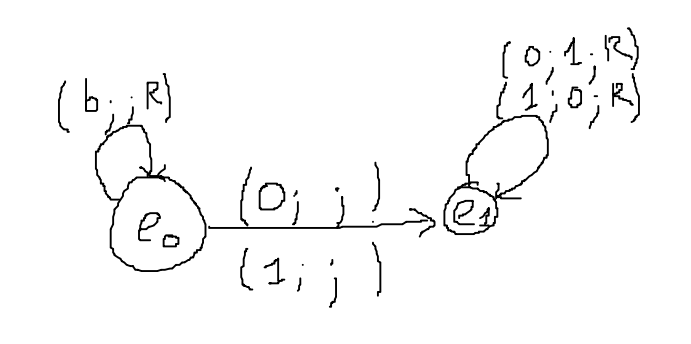
texte de remplacement

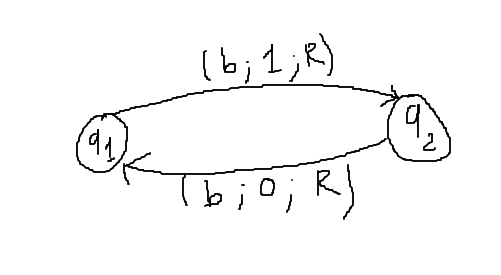
Un diagramme de la machine est un graphe orienté dont les sommets sont les états et les arcs représentent les passages possibles d'un état à un autre.

Dans cet exemple, on écrit une machine de Turing qui remplace les 0 par des 1 et les 1 par des 0.

Analyse du problème et liste des états à écrire.

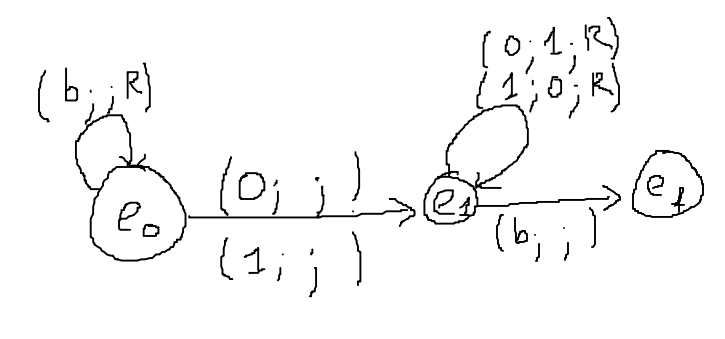
Cela peut donner le diagramme suivant : texte de remplacement

Réalisons la table des transitions de l'exemple précédent.

Etat Lit Ecrit Déplace Suivant
e0 blanc rien droite e0
0 rien rien e1
1 rien rien e1
e1 0 1 droite e1
1 0 droite e1
b rien rien ef
ef Arrêt de la machine

D'un point de vue machine, cela donnerait les représentations suivantes :

État initial : 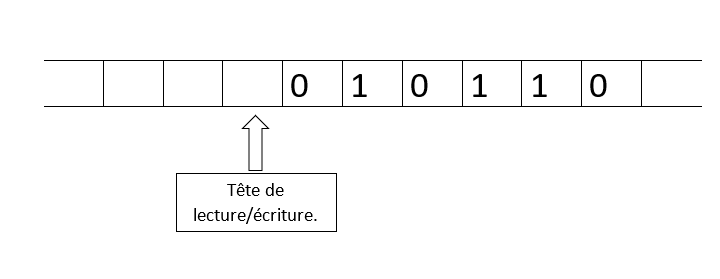texte de remplacement État final :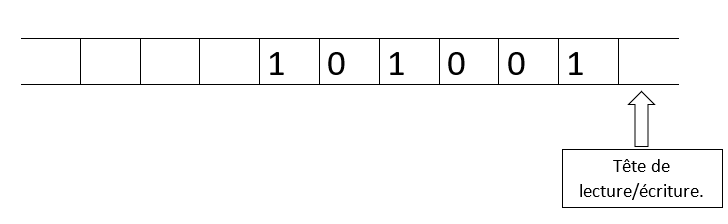 texte de remplacement

Écrire une machine de Turing qui remplace les 1 par des 0 et qui laisse les 0. Cette machine doit transformer le nombre 01010001 par 00000000.

D'un point de vue machine, cela donnerait les représentations suivantes :

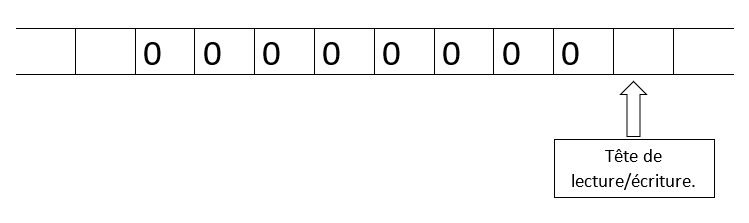
État initial : texte de remplacement État final : texte de remplacement

Vous écrirez le diagramme d'états ainsi que la table des transitions.

Analyse du problème et liste des états à écrire.

Code de déblocage de la correction :

Que produit la machine de Turing décrite par le diagramme suivant en partant d'un ruban vide ? texte de remplacement

Code de déblocage de la correction :

Un simulateur de machine de Turing (attention c'est le ruban qui se déplace ):

Source : INRIA-interstices-machine de Turing

Explications sur le simulateur

Un autre simulateur du site de M. PECHAUD (professeur en classe préparatoire)

Quelques liens et ressources :

La notion de programme en tant que donnée

Il est important de comprendre qu'un programme utilise des données sur lesquelles il travaille.
Ces données peuvent être également des programmes.

Le compilateur Python (ou les autres langages) est un programme (Edupython, Jupyter, idle de python, etc) qui utilise votre programme comme une donnée.

Voici par exemple le contenu d'un programme écrit en langage Python stocké dans un fichier nommé exemple_programme.py

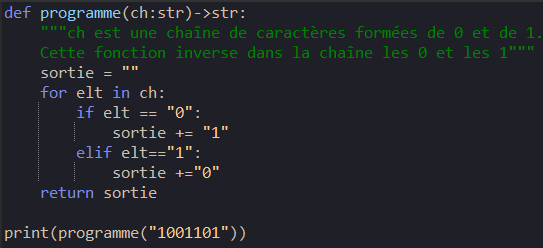
Pour exécuter ce programme, il vous suffit :

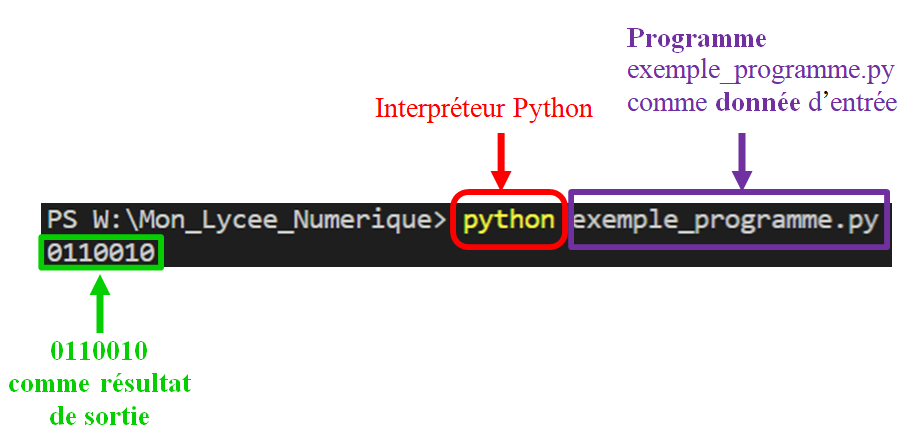
Voici d'autres exemples dans lesquels un programme est une donnée d'un autre programme :

Calculabilité et décidabilité

Calculabilité

Une fonction calculable est une fonction que l'on peut écrire sous forme d'algorithme.

La calculabilité ne dépend pas du langage utilisé.

Ainsi, si une fonction est calculable, il existe un algorithme dans le langage que vous utilisez qui permet de la calculer.

  1. Écrire la fonction successeur qui prend en paramètre un entier et qui renvoie son successeur en langage Python.

  2. Écrire la fonction successeur qui prend en paramètre un entier et qui renvoie son successeur en langage JavaScript.

  3. Écrire cette fonction à l'aide d'une machine de Turing, c'est-à-dire doner la table des transitions.

Code de déblocage de la correction :

Fonctions non-calculables : contrairement à ce que l'on pourrait imaginer, il existe des fonctions qui ne sont pas calculables. Il y en a même une infinité "plus grande" que de fonctions calculables.

La complexité de Kolmogorov est un exemple de fonction non-calculable.

La complexité de Kolmogorov est une fonction qui à tout objet associe la longueur du plus petit algorithme qui permet d'écrire ce nombre dans un language donné.

  • "Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!" peut être écrit en langage Python au moins de trois façons suivantes :

    • directement comme "Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!"

    • avec la fonction f suivant :

      def f():
    return "Bac!"*10

    • avec la fonction f anonymisée :

      f=lambda:"Bac!"*10

    Le dernier programme est celui nécessitant le moins de caractères (17), donc la complexité de l'objet "Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!Bac!" est d'au plus 17. (Il est peut-être possible d'écrire cet objet avec un code encore plus condensé en langage Python, d'où le "au plus").

  • Par contre une chaîne complètement aléatoire comme "a7G$ke5yTC/sw2J!O1f8MnGU6m.r?q" ne peut pas être déterminée par un algorithme de taille inférieure à la longueur de la chaîne.
    Sa complexité de Kolmogorov est au moins celle de sa longueur.

Prouvons, par un raisonnement par l'absurde, que la complexité de Kolmogorov est non-calculable.

Supposons que celle complexité soit calculable. Il existe donc une fonction kolmogorov qui à tout objet obj renvoie sa complexité de Kolmogorov.
Notons carac le nombre de caractères nécessaires pour écrire cette fonction kolmogorov.
Considérons cette fonction seuil_kolmogorov : 

def seuil_kolmogorov():
    n = 0
    while kolmogorov(n) < carac + 1000:
        n += 1
    return n

Cette fonction seuil_kolmogorov écrite en langage Python renvoie le plus petit entier naturel dont sa complexité de Kolmogorov dépasse ou égale $carac + 1000$.
Notons $min$ cet entier. Un tel entier existe forcément (d'où la terminaison du programme) car :

  • Il existe une infinité de nombres entiers,

  • Mais il n'existe qu'un nombre fini d'algorithmes que l'on peut écrire avec au plus $carac + 1000$ caractères (au plus $nombre\_caractère^{carac + 1000}$) donc a fortiori il existe un nombre fini d'algorithmes écrit avec au plus $carac + 1000$ caractères donnant comme résultat un nombre entier.

Cette fonction seuil_kolmogorov est un algorithme qui renvoie l'entier $min$ et qui s'écrit avec moins de 1000 caractères donc strictement moins que $carac + 1000$. Par définition de la complexité de Kolmogorov, kolmogorov(min)$\lt 1000$.

Cependant, par définition de $min$, $min$ est un nombre entier tel que kolmogorov(min)$\ge carac + 1000$, c'est même le plus plus petit entier vérifiant cela.

Ainsi, on a à la fois :

  • kolmogorov(min)$\lt 1000$.

  • kolmogorov(min)$\ge carac + 1000 \gt 1000$.

On aboutit à une contradiction absurde.
Cela signifie que l'hypothèse initiale "la complexite de Kolmogorov est calculable" est fausse.
On a prouvé par un raisonnement par l'absurde que la complexité de Kolmogorov est une fonction non calculable.

Les curieux.ses peuvent aussi aller voir la notion de fonctions des castors affairés.

Décidabilité

Une propriété est décidable s'il existe un algorithme qui la confirme ou l'infirme en un nombre fini d'étapes. L'algorithme doit répondre par oui ou par non à la question posée par le problème. On parle dans ce cas de problème de décision.

Il existe des propriétés non décidables.

Le problème de l'arrêt est non décidable

Il nous est arrivé à tous d'écrire une boucle infinie. C'est le drame car notre programme ne s'arrête jamais. Dans certains domaines, ce problème devient un problème essentiel. Pensez aux problèmes de sécurité (centrale nucléaire, aviation, transports, etc).

Il est donc naturel de se poser cette question :

Peut-on écrire un algorithme capable de prédire que n'importe quel programme va s'arrêter ? La réponse est non. On dit que le problème de l'arrêt d'un programme est indécidable.

Des exemples de programmes qui ne s'arrêtent pas.

Que pensez-vous du script suivant ?

def est_pair(n:int)->bool :
    """Renvoie true si n  est pair"""
    assert(isinstance(n, int)) # Test si n est entier
    test = False
    if n%2 == 0 : test = True
    return test

def infini(n: int) : 
    while est_pair(n):
        n = n*2
    return n

print(infini(5))
print(infini(4))

Vous pouvez si besoin tester ce code dans ce trinket

Code de déblocage de la correction :

Inventer une boucle infinie qui ne soit pas triviale.

Code de déblocage de la correction :

Démonstration par l'absurde de la non décidabilité du problème de l'arrêt d'un programme.

Le raisonnement par l'absurde est une manière de raisonner qui consiste à démontrer la vérité d'une proposition en prouvant l'absurdité du contraire de celle-ci.
Synonyme : apagogie.

Lorsque l'on cherche à démontrer une propriété par l'absurde, on prend comme hypothèse la proposition contraire et on en déduit une (ou des) conséquence(s) absurdes.

Il existe de nombreux exemples en mathématiques de raisonnement par l'absurde :

Pour ceux et celles voulant développer ou mieux comprendre le raisonnement par l'asurde, il vous suffit de consulter ce cours de maths expertes.

Nous allons utiliser ce moyen pour démontrer la propriété suivante :

Le problème de l'arrêt d'un programme est indécidable.

En voici une démonstration à comprendre et connaître :

Raisonnons par l'absurde.

Dans un premier temps, on fait l'hypothèse que l'on est capable de construire un algorithme nommé halt qui résout le problème de l'arrêt d'un programme.
L'objectif est de démontrer que cette hypothèse est fausse.

En pseudo-langage, cette fonction halt peut être vue ainsi : 

fonction halt(P : programme) : booléen
    si P s'arrête alors on renvoie vrai
    sinon on renvoie faux

On construit maintenant un deuxième algorithme que l'on appelle contradiction qui :

procédure contradiction(P : programme)
    test←halt(P)
    si test=vrai alors on exécute une boucle infinie
    sinon on affiche "stop"

On applique maintenant la procédure contradiction à elle même. On exécute ainsi contradiction(contradiction).

  1. On appelle halt(contradiction).

  2. Deux cas possibles :

    • Soit le programme contradiction s'arrête alors halt(contradiction) renvoie vrai. Mais dans ce cas le programme contradiction ne s'arrête pas car on exécute une boucle infinie.

    • Soit le programme contradiction ne s'arrête pas alors halt(contradiction) renvoie faux. Mais dans ce cas le programme contradiction s'arrête en affichant "stop".

On obtient donc une contradiction : contradiction(contradiction) aboutit à deux cas contradictoires.
Par ce raisonnement par l'absurde, notre hypothèse de départ : "on est capable de construire un algorithme halt qui résout le problème de l'arrêt d'un programme" est fausse.

Nous venons donc de démontrer que le programme de l'arrêt est indécidable.

Vous retrouverez cette démonstration dans cette vidéo.

Pour les curieux : la notion en logique de paradoxe.

Intéressez vous à la proposition suivante : "je suis un menteur".

Considérons que ce que je dis est vrai : je suis un menteur. Mais étant que menteur, si je dis que je suis un menteur alors ce que je dis est faux, donc je ne mens pas. Mais j'ai donc menti en disant que je suis un menteur.

Maintenant, considérons que ce que je dis est faux, c'est-à-dire qu'en fait je ne suis pas menteur. Comme je ne mens pas alors ce que je dit est vrai, en particulier mon affirmation "je suis un menteur".
Je dis donc le contraire de la vérité donc je mens, ce qui contredit mon hypothèse de départ.

Dans les deux cas j'aboutit à une absurdité ! Cette proposition est donc ni vraie, ni fausse : quel paradoxe !

Ce paradoxe du menteur serait attribué à Epiménide le Crétois (VIIème sicle av J-C).

On parle dans ce cas d'autoréférence, c'est-à-dire une phrase ou une formule qui fait référence à elle même.
Cette notion a beaucoup d'applications en mathématiques, philosophie et en programmation. Un énoncé contenant une autoréférence est parfois paradoxal.

En 1931, Kurt Gödel, pour démontrer son théorème d'incomplétude, utilise un énoncé inspiré de ce paradoxe.

Pour aller plus loin

Savoir et Savoir faire

▲