Dans ce cours nous allons aborder la notions de structure de données abstraites.
Nous allons à travers des exemples voir ce qu'est l'interface d'une structure de données. Nous allons par la suite implémenter ces structures en Python.
Interface d'une structure de données abstraites
Structure de données abstraites
Un type abstrait ou une structure de données abstraite est une spécification mathématique d'un ensemble de données et de l'ensemble des opérateurs associés.
On qualifie d'abstrait ce type de données car il correspond à un cahier des charges qu’une structure de données doit ensuite implémenter.
Dans ce cours, nous allons aborder deux structures de données abstraites : la pile et la file.
La structure du tableau est une structure de donnée non abstraite. Nous verrons une description de cette structure dans la suite de ce cours.
L'étude des structures de données abstraites permettent de choisir des structures qui simplifient la compréhension des algorithmes mais surtout qui permettent d'optimiser en coût de nombreux algorithmes.
Un premier exemple : la pile
Pile
Une pile est :
- soit vide ;
- soit une cellule à deux champs, un champ contenant un élément, et un champ contenant une autre pile.
On dit que cette structure de donnée est de type LIFO : Last In First Out
On pourra représenter une pile de la manière suivante :$$P=(hautDeLaPile,resteDeLaPile).$$
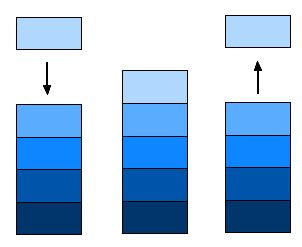
Essayons de comprendre ce que cette définition implique :
Pour pouvoir travailler avec des données structurées en pile, il faut déjà pouvoir créer une pile vide. Nous devons nous doter d'une notation synthétique et compréhensible. Pour créer une pile P vide on écrira :
P=vide()
Créer une Pile vide
La structure pile dispose d'un opérateur pour créer une pile P vide. On notera dans ce cours
P=vide()
Pour appliquer la définition à un objet P, nous devons savoir si P est vide ou non. Il faut donc se doter d'un opérateur estVide qui a un objet de type pile P renvoie un booleen : Vraie si la P est vide et Faux sinon.
La fonction estVide()
A toute pile $P$ :
- $estVide(P)=Vraie$ si $P$ est vide
- $estVide(P)=Faux$ si $P$ n'est pas vide.
Si cette pile n'est pas vide, elle se compose de deux champs : un premier contenant un élément de type élémentaire ( booléen, entier,flottant) et un second de type pile.
Cette définition est donc récursive : une pile est définie à partir d'une pile.
Nous savons ce qu'est une pile vide. C'est une pile dont l'application de l'opérateur
estVide renvoie vraie.
Une pile a un élément est composé dans le haut de sa pile par l'élément et d'une pile vide. Nous avons ainsi compris ce qu'est une pile à un élément :
(a,vide())
Une pile à deux éléments peut être représentées ainsi :
(hautDeLaPile,(secondElementDeLaPile,vide()))



Prenons un exemple, on aimerait ranger un groupe d'individus dans un objet de type pile :
Anakin ; Boba Fett ; Dark Vador ; Han Solo ; Yoda
Une représentation de ces données en pile serait :
P=(Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide())))))
Le haut de la pile est $Anakin$ et le reste est $(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide()))))$.

- Donner une représentation en pile de cette ensemble de couleur : rouge ; bleu ; vert. On nommera cette pile $P_{couleur}$.
- Donner une représentation en pile de cette ensemble de nombre : 12 ; 5 ; 3 ; 6 ; 1. On nommera cette pile $P_{entier}$.
A ce stade, vous avez compris ce qu'est une structure de données pile. Essayons de voir comment manipuler un objet de ce type.
Empiler un élément en haut de pile
Soit $P$ une pile, la pile obtenue en empilant un élément $a$ en haut de $P$ est la pile $(a, P)$.
On notera cet opérateur $empiler(a, P)$
En reprenant l'exemple précédent où $ P =(Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide())))))$; $empiler(Luke,P)$ est la pile :
$(Luke,(Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide()))))))$

Reprendre l'exercice précédent et ajouter le violet à $ P _{couleur}$.
Dépiler le haut d'une pile
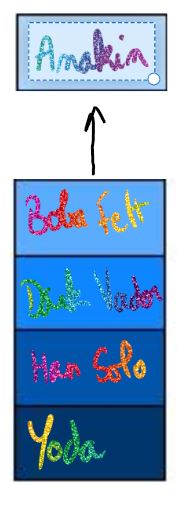
Soit $P_1$, $P_2$ deux piles et $a$ le haut de la pile de $P_1$, la pile obtenue en dépilant l'élément $a$ de pile de $P_1$ est la pile $P_2$.
On notera cet opérateur $depiler(P_1)$, elle transforme la pile initiale et renvoie l'élément dépiler.

En reprenant l'exemple précédent où $P=(Anakin,(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide())))))$; la commande $depiler(P)$ transforme la pile P en : $(Boba Fett,(Dark Vador,(Han Solo,(Yoda,vide()))))$ et renvoie Anakin.
Reprendre l'exercice précédent et retirer la première couleur.
Interface d'une structure de donnée : définition
Interface d'une structure de données abstraite
L'interface d'une structure de données abstraite est l'ensemble des opérateurs nécessaires à la manipulation de cette structure.
Interface de la pile
L'interface de la structure pile est l'ensemble des opérateurs vu précédemment :
- $vide()$
- $estVide(P)$
- $empiler(a,P)$
- $depiler(P)$
Nous pourrions ajouter d'autres éléments à l'interface mais l'objectif et d'avoir une interface minimale qui permettent de manipuler cette structure.
Il peut être intéressant de connaitre le nombre d'éléments dans une pile.
En voila un pseudo-code :
nombreElement=0
while estVide(P) est faux
nombreElement+=1
depiler(P)
renvoyer nombreElement
Nous n'avons donc pas besoin d'ajouter un opérateur qui compterait le nombre d'éléments d'une pile.
Ecrire un script en pseudo-code qui permet de supprimer le premier élément du reste d'une pile.
Correction :
a=depiler(P)
depiler(P)
empiler(a,P)
L'interface de la file
La file
Une file est :
- soit vide ;
- soit une cellule à trois champs, un champ tête , un champ queue et un champ contenant une file.
Une structure de File fonctionne sur le principe premier entré − premier sorti (comme les files d’attentes à un guichet) FIFO : First In First Out.
On pourra représenter une file de la manière suivante :$$F=(teteDeLaFile, queueDeFile, coeurDeFile).$$
-
Prenons un exemple, on aimerais ranger un groupe d'individu dans un objet de type file
Anakin; Boba Fett; Dark Vador; Han Solo; Yoda
une représentation en de la file correspondante est :
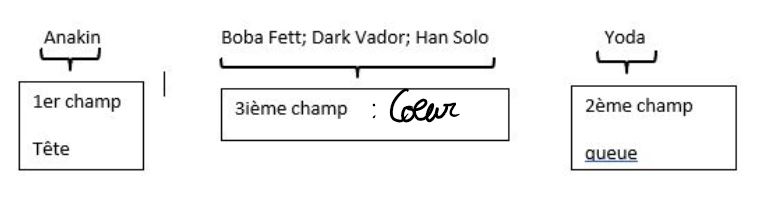
- Une file à un élément a pour :
- tête : vide
- queue : le seul élément
- troisième champ : vide
- Une file à deux éléments a pour :
- tête : un élément
- queue : un élément
- troisième champ : vide.
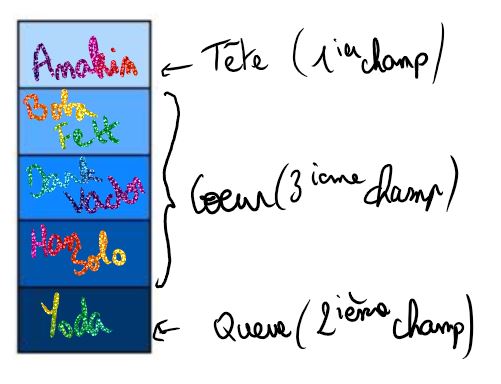
Définir une file vide
Une file est vide si sa queue est vide.
Pour affecter à une variable $F$ une file vide, on notera : $F=vide()$.
définir enfiler(a,F)
la nouvelle file obtenue à l'enfilement de a sur $F$ est la file :
- de tête celle de $F$ ;
- de queue a ;
- et de troisième champ enfiler(troisième champ de $F$, queue de $F$).
Cet opérateur est récursif.
En reprenant l'exemple précédent où $F =(Anakin,Yoda,(Boba Fett,Dark Vador,Han Solo)))$; $enfiler(Luke,F)$ est la file :
$F=(Anakin,Luke,(Boba Fett,Dark Vador,Han Solo,Yoda)))$
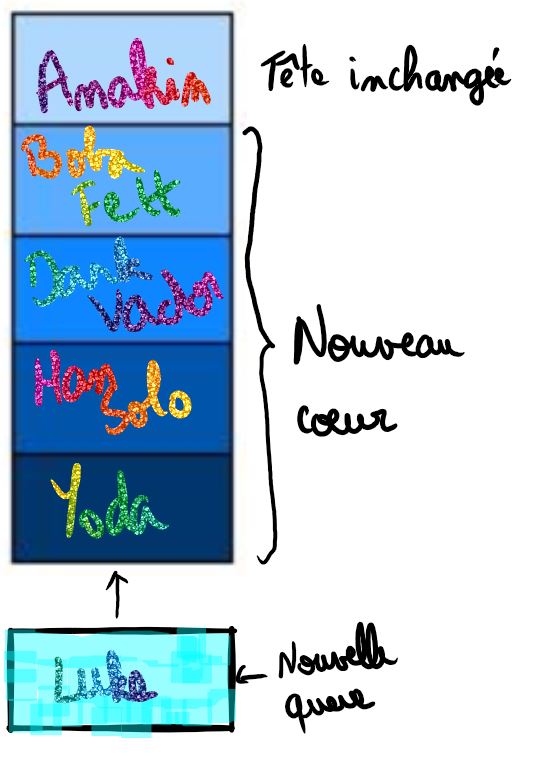
définir defiler($F$)
la nouvelle file obtenue par défilement de $F$ est la file:
- de tête , la tête du troisième champ de $F$ ;
- de queue celle de $F$ ;
- et de troisième champ défiler(du troisième champ de $F$) .
Cet opérateur est récursif.
Cet opérateur transforme $F$ et renvoie la tête de $F$
En reprenant l'exemple précédent où $F=(Anakin,Yoda,(Boba Fett,Dark Vador,Han Solo))$; la commande $defiler(F)$ transforme la file $F$ en : $(Boba Fett,Yoda,(Dark Vador,Han Solo))$ et renvoie Anakin.
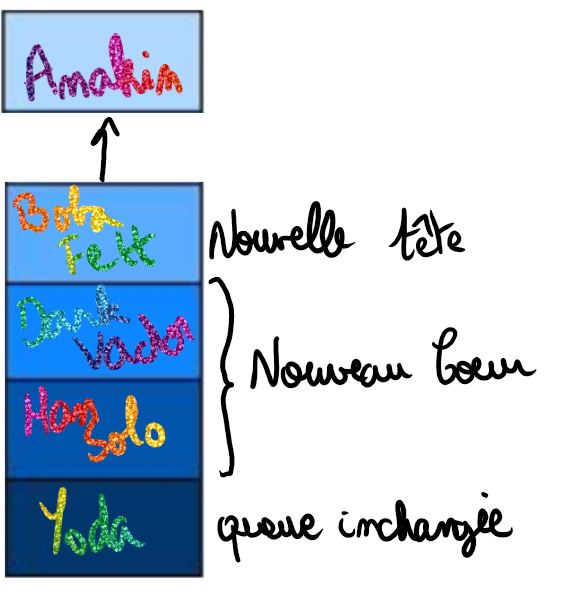
interface d'une file
L'interface de la structure de file est composée de :
- $vide()$
- $estVide(F)$
- $enfiler(a,F)$
- $defiler(F)$
Il peut être intéressant de connaitre le nombre d'éléments dans une file.
En voila un pseudo-code :
nombreElement=0
while estVide(F) est faux
nombreElement+=1
defiler(F)
renvoyer nombreElement
Ecrire un script en pseudo-code qui permet de supprimer le premier élément du troisième champ.
Implémentation
Implémentation
Implémenter une structure de données à travers une structure existante c'est écrire les éléments de l'interface à l'aide des outils proposées par la structure de données existante.
Tableau
Tableau
Un tableau est une structure de données avec une taille fixe où chacune des cases est indexée. On peut accéder à une case connaissant son index.
Accès à une valeur d'un tableau
Pour accéder à une valeur indexée $i$ dans un tableau T. On écrira T[i].
On peut réaffecter une valeur du tableau par une autre à partir de son index.
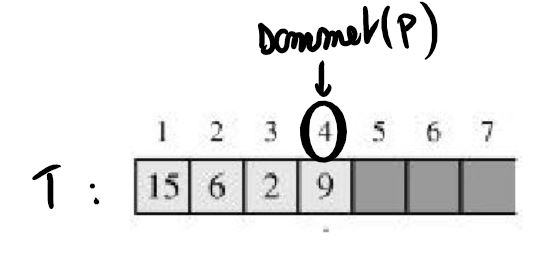
Ce tableau a une longueur maximale de 7. T[1]=15. T[5] est vide.
implémentation des piles avec des tableaux
Soit $P$ une pile.
On dispose d'un tableau nommé $T$ avec $n$ emplacements.
Il est possible d’implémenter la pile $P$ d’au plus $n$ éléments avec le tableau $T$.
Le tableau possède un attribut $sommet(P)$ qui indexe l’élément le plus récemment inséré.
La pile est constituée des éléments $T[1 . . sommet(P)]$, tous ceux compris entre $T[1]$, l’élément situé à la base de la pile, et $T[sommet(P)]$, l’élément
situé au sommet.
La donnée de la pile se constitue donc de la donnée de $T$ et de la valeur de $sommet(P)$.
On considère la pile $(9,(2,(6,(15,vide()))))$. Son implémentation se compose de la donnée du tableau T:

et de $sommet(P)=4$.
$sommet(P)$ est un index du tableau, pas un élément de la pile.
Implémentation de la fonction estVide(P)
estVide(paramètre : P)
si sommet(P)=0 //signifie que le tableau est vide
alors retourner VRAI
sinon retourner FAUX
Implémentation de la procédure empiler(a,P)
empiler(paramètres : a,P)
si sommet(P)=n //signifie que le tableau est complet
alors afficher "espace insuffisant"
sinon
sommet(P)←sommet(P)+1
T[sommet(P)]←a
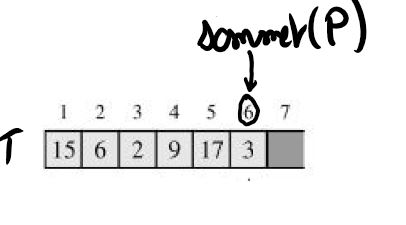
Si on lance empiler(17,P) puis empiler(3,P) on obtient cette représentation :
Implémentation de la fonction depiler(P)
depiler(paramètre : P)
si sommet(P)=0
alors afficher "pile vide"
sinon sommet(P)←sommet(P)-1
retourner T[sommet(P)+1]
On observe que la procédure empiler ne renvoie rien alors que la fonction depiler renvoie un élément de la pile.
Si on lance depiler(P) on obtient :
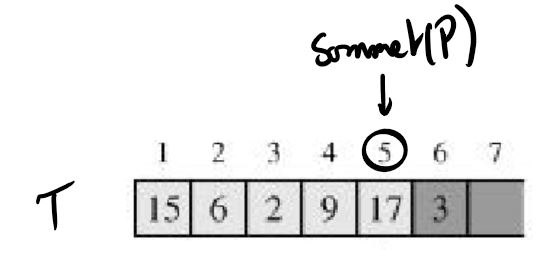
Observer que T[6] a encore un sens pour le tableau mais plus pour la pile.
On considère la pile dont la représentation en tableau est :

Pour chaque question, on repartira du tableau de départ.
- Qu'obtient-on si on lance successivement
depiler(P),depiler(P),depiler(P)etdepiler(P). - Qu'obtient-on si on lance successivement
depiler(P),depiler(P),depiler(P),depiler(P)etdepiler(P). - Qu'obtient-on si on lance successivement
empiler(3,P),empiler(5,P)etdepiler(P)
implémentation des files avec des tableaux
On dispose d'un tableau nommé $T$ avec $n$ emplacements.
Il est possible d’implémenter une file $F$ d’au plus $n$ éléments avec le tableau $T$.
Le tableau possède un attribut $tete(F)$ qui indexe l’élément de tête et un attribut $queue(F)$ qui indexe l'emplacement où un nouvel élément sera inséré. $T[queue(F)]$ est vide au sens de la file.
La file est constituée des éléments $T[tête(F) . . queue(F)-1]$.
Avec cette implémentation $T[n+1]$ doit pointer vers $T[1]$ au sens de la file. Une façons de visualiser cette implémentation est un tableau circulaire où le début du tableau et la fin du tableau seraient reliés.
Les éléments de la file se trouvent aux emplacements $tete(F)$, $tete(F) +1$, . . . , $queue(F) − 1$, après quoi l’on « boucle » : l’emplacement 1 suit immédiatement l’emplacement $n$ dans un ordre circulaire.
Dans cette implémentation la queue est vide
La donnée de la file se constitue de la donnée d'un tableau $T$, de la valeur de $tete(F)$ et de $queue(F)$.
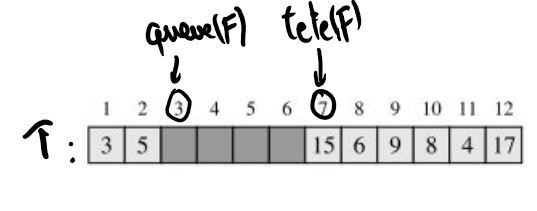
Une représentation de l'implémentation avec un tableau $T$ de la file $F=(15,4,(6,9,8))$ est :
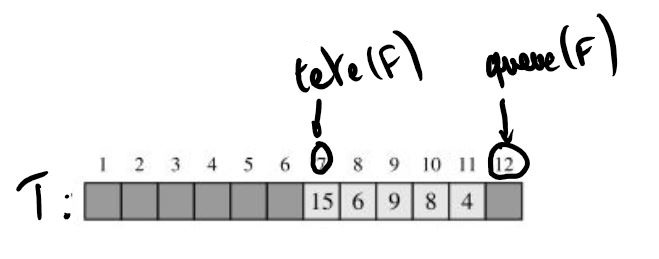
- Quand $tete(F) = queue(F)$, la file est vide.
- Quand $tete(F) = queue(F) + 1$, la file est pleine.
- $queue(F)$ est vide au sens de la file. Si $tete(F) = queue(F)$ alors la tête est vide, c'est que la file est vide.
- L'emplacement $queue(F)$ doit toujours être vide au sens de la file. Si $tete(F) = queue(F) + 1$, le prochain enfilage fera que $tete(F) = queue(F)$
Implémentation de la fonction estVide(F)
estVide(P)
si queue(F)=tete(F)
alors retourner VRAI
sinon retourner FAUX
Implémentation de la fonction enfiler(a,F)
enfiler(a,F)
T(queue(F))←a
si queue(F)=n
alors queue(F)←1
sinon queue(F)←queue(F)+1
On dispose d'une file dont la représentation de l'implémentation en tableau est :

Si on lance enfiler(17,F) puis enfiler(3,F) et enfin
enfiler(5,F), on obtient cette représentation :
Implémentation de la fonction defiler(F)
defiler(F)
x←T[tete(F)]
si tete(F)=n
alors tete(F)←1
sinon tete(F)←tete(F)+1
retourner x
On dispose de la file de l'exemple précédent :

Si on lance defiler(F), on obtient :
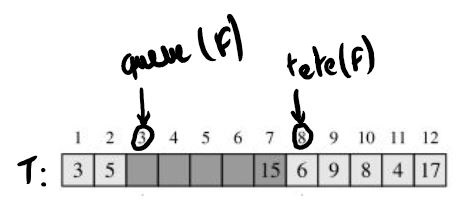
Observer que T[7] a encore un sens pour le tableau mais plus pour la file.
On considère la file dont la représentation de l'implémentation en tableau est :
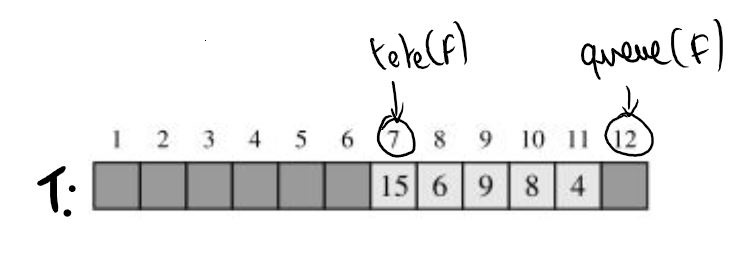
- Qu'obtient-on si on lance successivement
defiler(F),defiler(F),defiler(F)etdefiler(F). - Qu'obtient-on si on lance successivement
defiler(F),defiler(F),defiler(F),defiler(F)etdefiler(F). - Qu'obtient-on si on lance successivement
enfiler(3,F),enfiler(5,F)etdefiler(F)
Reprendre les fonctions $enfiler()$ et $defiler()$ et y ajouter les erreurs de dépassements d'écritures.

NSI de Auteurs : Jean-Christophe Gérard, Thomas Lourdet, Johan Monteillet, Pascal Thérèse est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.