Demandez le programme !

Savoir ce qu'est une structure linéaire.

Les arbres

Nous allons travailler sur la structure de donnée "arbre". Cette structure n'est pas linéaire mais hiérarchique.

Arbre

Un arbre est une structure de données constituée de nœuds.

Le sommet de l'arbre s'appelle la racine.

Le nœud $B$ situé sous un nœud $A$ est appelé enfant du nœud $A$

Un nœud qui ne possède pas d'enfant est appelé feuille.

Les nœuds autre que la racine et les feuilles sont appelés nœuds internes.

Une branche est une suite de nœud consécutifs de la racine vers une feuille.

Dans cet arbre:

il y a 10 nœuds.
Le nœud $A$ est la racine.
Il y a 5 feuilles donc 5 branches.
Le nœud $D$ est l'enfant du nœud $C$.
Il y a 4 nœuds internes.
La succession $A-C-D-F-Z$ est la branche menant à la feuille $Z$ depuis la racine $A$.

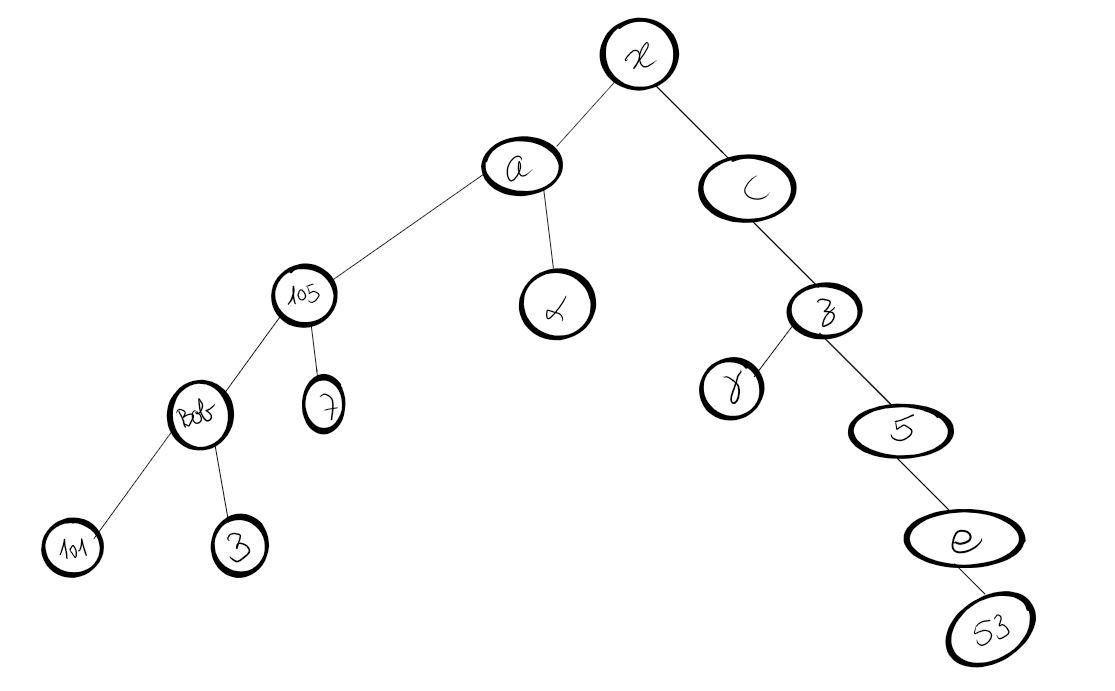
On donne l'arbre suivant :

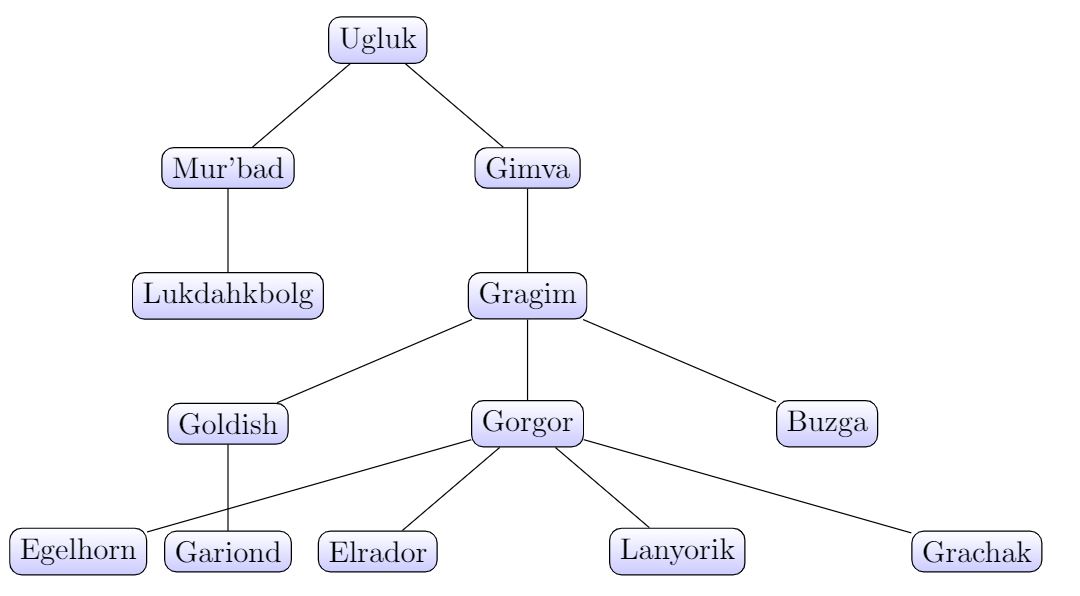
Quelle est la racine de cet arbre ?
Combien y-a-t-il de nœuds ?
Combien y-a-t-il de feuilles ?
Combien y-a-t-il de branches ?
L'ensemble des nœuds internes compte combien d'éléments ?
Quels sont les enfants de Gragim ?

On peut caractériser un arbre par différentes caractéristiques :

Son arité : le nombre maximal d'enfants qu'un nœud peut avoir.
Sa taille : le nombre de nœuds qui le composent.
Sa hauteur : le nombre de nœuds qui constituent la branche contenant le plus de nœuds sans compter la racine.

On reprend l'arbre de la définition d'un arbre :

L'arité de cet arbre est 3.
La taille de cet arbre est 10.
La hauteur de cet arbre est 4.

On donne l'arbre suivant :

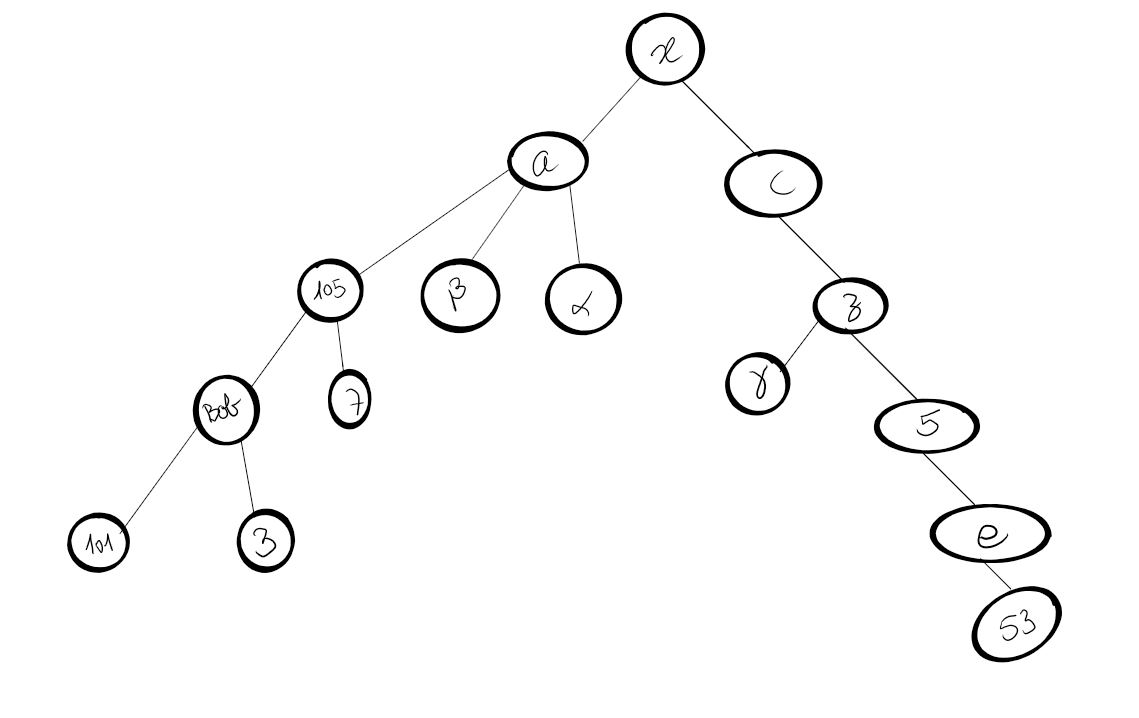
Déterminer l'arité, la taille et la hauteur de cet arbre.

On donne le répertoire à télécharger ici

Représenter l'arborescence des répertoires et des fichiers à l'aide d'un arbre.

Arbres binaires

Définitions

Arbres binaires

On appelle arbre binaire un arbre d'arité inférieure ou égale à 2.

Les arbres binaires sont constitués de nœuds de 0, 1 ou 2 enfants.

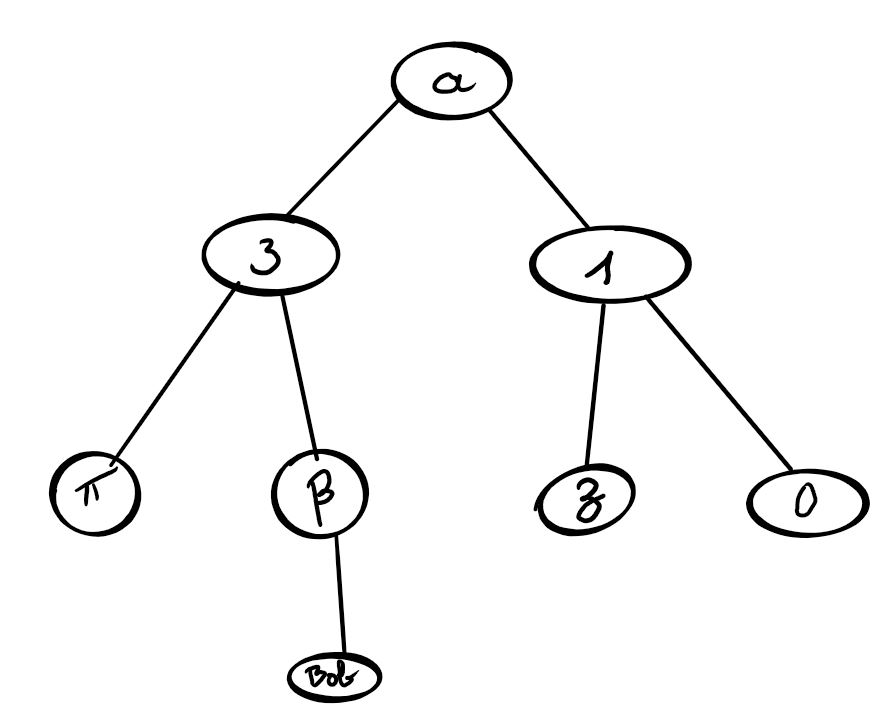
Sous-arbre droit/gauche

Quand un nœud a deux enfants, il possède un sous-arbre gauche et un sous-arbre droit.

Pour un nœud $\alpha$, on notera :

$gauche(\alpha)$ le sous-arbre gauche du nœud $\alpha$ ;
$droit(\alpha)$ le sous-arbre droit du nœud $\alpha$.

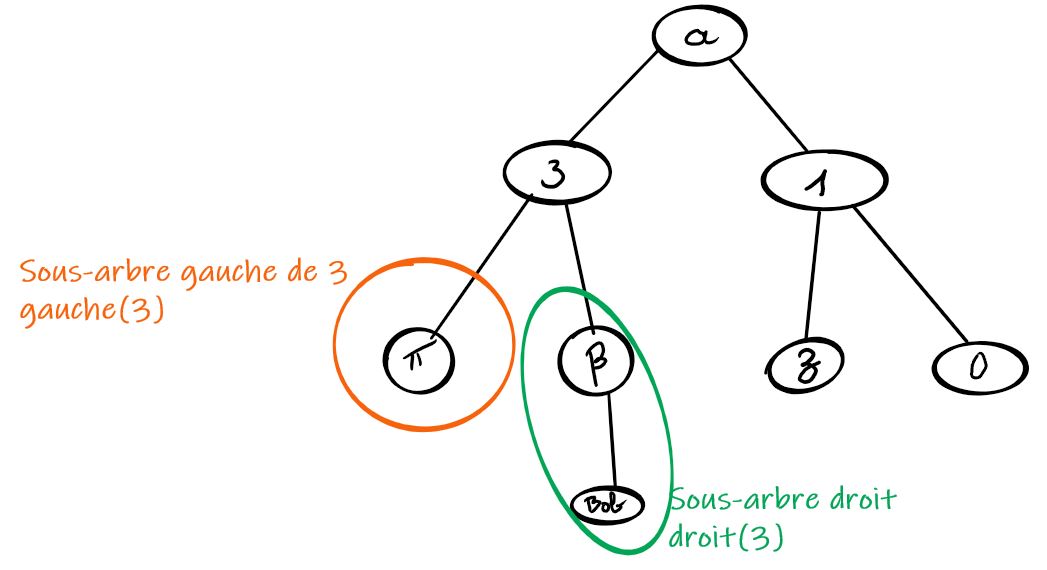
Remarquez bien que les sous-arbres gauche et droit sont aussi des arbres binaires, si bien que les arbres binaires ont naturellement une structure récursive.
C'est la raison pour laquelle, plusieurs fonctions définies par la suite et portant sur les arbres seront définies elles aussi de manière récursive.

Parmi les arbres suivants, lesquels sont binaires?

Mesures sur les arbres binaires

Les arbres binaires étant particuliers, on peut calculer un certains nombres de caractéristiques d'un arbre binaire.

La taille d'un arbre B correspond au nombre de ses nœuds, elle est définie par :

$Taille(B) = 0$, si $B$ est un arbre vide.
$Taille(B) = 1 + Taille(gauche(racine(B))) + Taille(droit(racine(B)))$ sinon.

On donne l'arbre suivant :

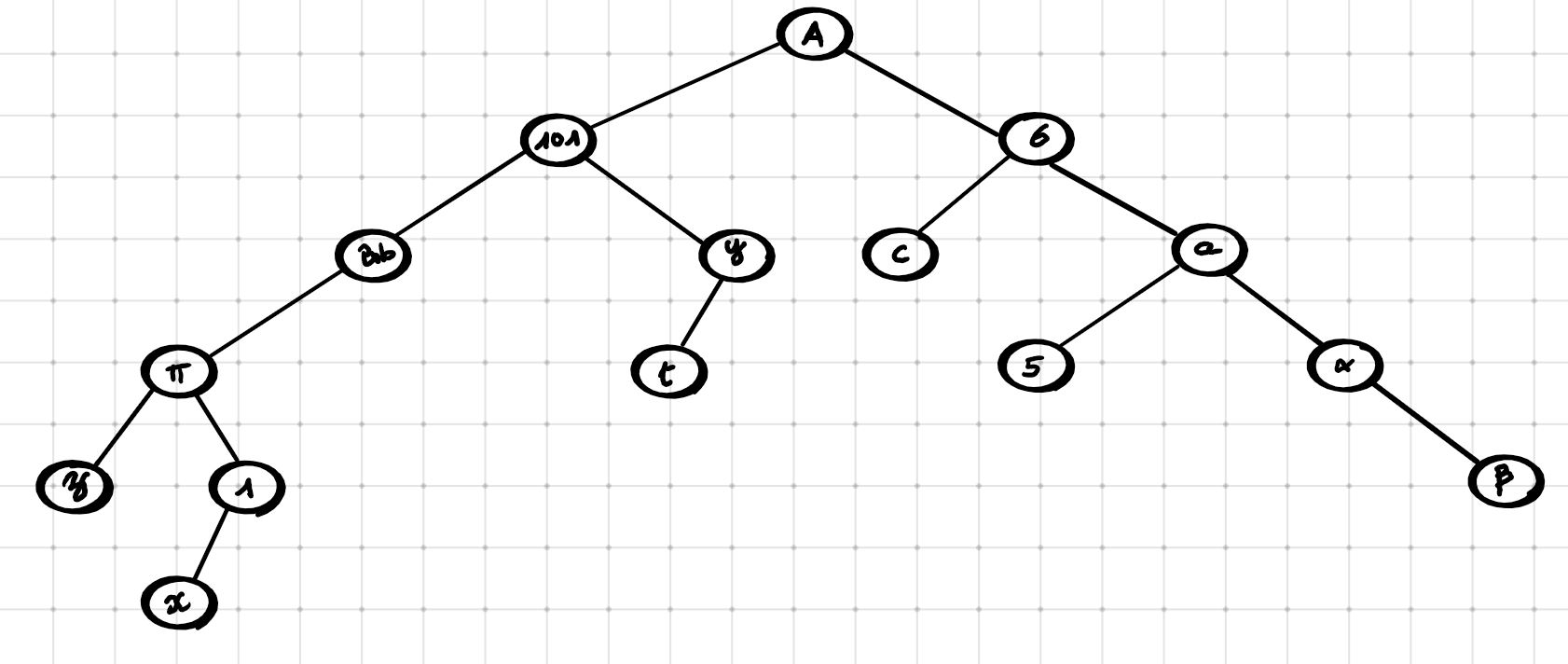
Déterminer la taille de cet arbre.

On peut refaire l'exercice en travaillant de manière récursive.

La hauteur d'un nœud ou la profondeur de $x$ correspond au nombre d'arêtes au-dessus $x$ pour revenir à la racine, elle est définie par :

$HauteurDeNoeud(x) = 0$, si $x$ est la racine de l'arbre.
$HauteurDeNoeud(x) = 1 + HauteurDeNoeud(y)$ si $y$ est le père de $x$.

On donne l'arbre suivant :

Déterminer la hauteur des nœuds $Bob$ et $\alpha$.

La hauteur d'un arbre B correspond au nombre d'arêtes entre la racine et la feuille la plus éloignée :

$Hauteur(B) = Max(HauteurDeNoeud(x))$, où $x$ qui décrit l'ensemble des nœuds de B.

Considérons $B$ un arbre binaire non vide.
Nommons $gauche(B)$ le sous-arbre gauche (éventuellement vide) de la racine de $B$ et $droit(B)$ les sous-arbre droit (éventuellement vide) de la racine de $B$.

La $Hauteur$ d'un arbre binaire $B$ non vide peut être définie de manière récursive ainsi :

Si l'arbre $B$ est réduit à sa racine alors $Hauteur(B) = 0$.
Sinon, $Hauteur(B) = 1 + max(Hauteur(gauche(B)), Hauteur(droit(B)))$

On donne l'arbre suivant :

Déterminer la hauteur de cet arbre.

La longueur de cheminement d'un arbre B correspond à la somme des hauteurs de chacun des nœuds. :

$LC(B)=$somme de tous les $H(x)$, où $x$ qui décrit l'ensemble des nœuds de B.
Autrement dit : $LC(B)=\sum\limits_{i=1}^{T(B)}H(x_i)$.

On donne l'arbre suivant :

Déterminer la longueur de cheminement de cet arbre.

La longueur de cheminement externe d'un arbre B correspond à la somme des hauteurs de chacune des feuilles :

$LCE(B)=$somme de tous les $H(f)$, où $f$ décrit l'ensemble des feuilles de B.
Autrement dit : $LCE(B)=\sum\limits_{i=1}^{NF}H(f_i)$ où $NF$ est le nombre de feuilles.

On donne l'arbre suivant :

Déterminer la longueur de cheminement externe de cet arbre.

La longueur de cheminement interne d'un arbre B correspond à la somme des hauteurs des nœuds internes de B :

$LCI(B)=$somme de tous les $H(x)$, où $x$ décrit l'ensemble des nœuds internes de B.
Autrement dit : $LCI(B)=\sum\limits_{i=1}^{T(B)-NF}H(x_i)$ où $x_i$ est un nœud interne.

On donne l'arbre suivant :

Déterminer la longueur de cheminement interne de cet arbre.

Déterminer une relation entre $LC(B)$, $LCE(B)$ et $LCI(B)$.

La profondeur moyenne d'un arbre B est définie par : $$PM(B)=\frac{LC(B)}{T(B)}$$

On donne l'arbre suivant :

Déterminer la profondeur moyenne de cet arbre.

La profondeur moyenne externe d'un arbre B est définie par : $$PME(B)=\frac{LCE(B)}{NF}$$

$NF$ désigne ici le nombre de feuilles.

On donne l'arbre suivant :

Déterminer la profondeur moyenne externe de cet arbre.

La profondeur moyenne interne d'un arbre B est définie par : $$PMI(B)=\frac{LCI(B)}{T(B)-NF}$$

On donne l'arbre suivant :

Déterminer la profondeur moyenne interne de cet arbre.

La longueur de cheminement et la profondeur moyenne seront utiles pour les algorithmes sur les arbres binaires.

On donne l'arbre $B$ suivant :

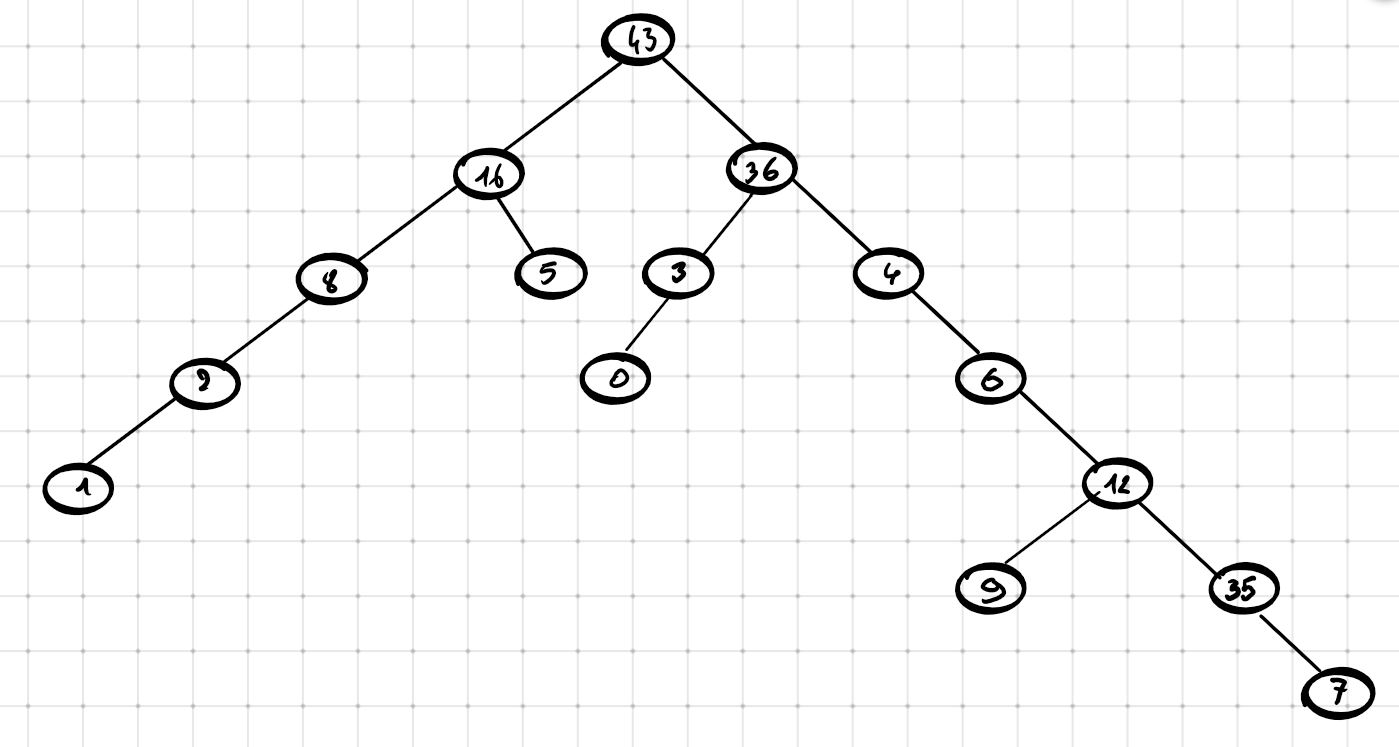
Déterminer :

la racine,
le nombre de feuilles,
le nombre de branches,
l'arité,
sa taille $T(B)$,
La hauteur de $B$, $H(B)$,
$LC(B)$,
$LCE(B)$,
$LCI(B)$,
$PM(B)$,
$PME(B)$,
$PMI(B)$.

Arbre binaire de recherche

Un arbre binaire de recherche est un arbre binaire dans lequel l'étiquette d'un nœud est appelé clé et est un entier. L'arbre binaire vérifie deux propriétés :

Les clés de tous les nœuds du sous-arbre gauche d'un nœud $x$ sont inférieures ou égales à la clé de $x$.
Les clés de tous les nœuds du sous-arbre droit d'un nœud $x$ sont strictement supérieures à la clé de $x$.

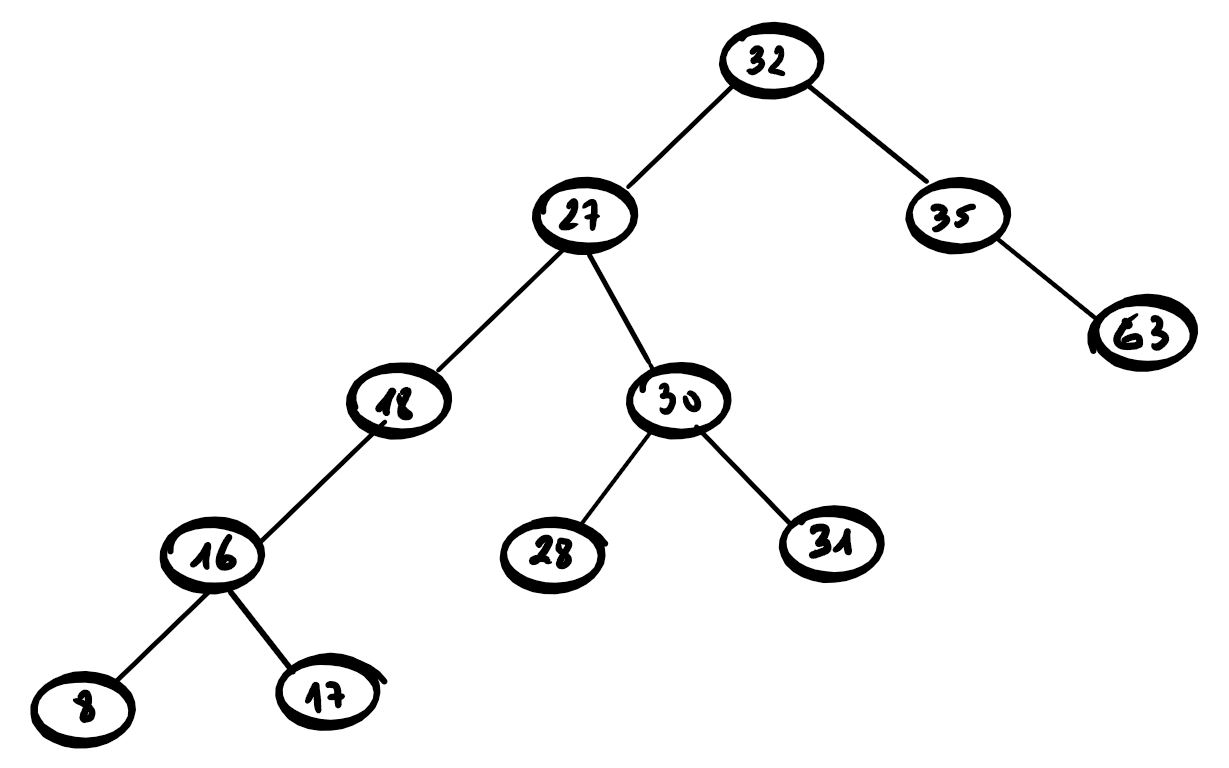
Quels sont parmi les arbres proposés ci-dessous les arbres binaires de recherche?

Compléter cet arbre pour que ce soit un arbre binaire de recherche :

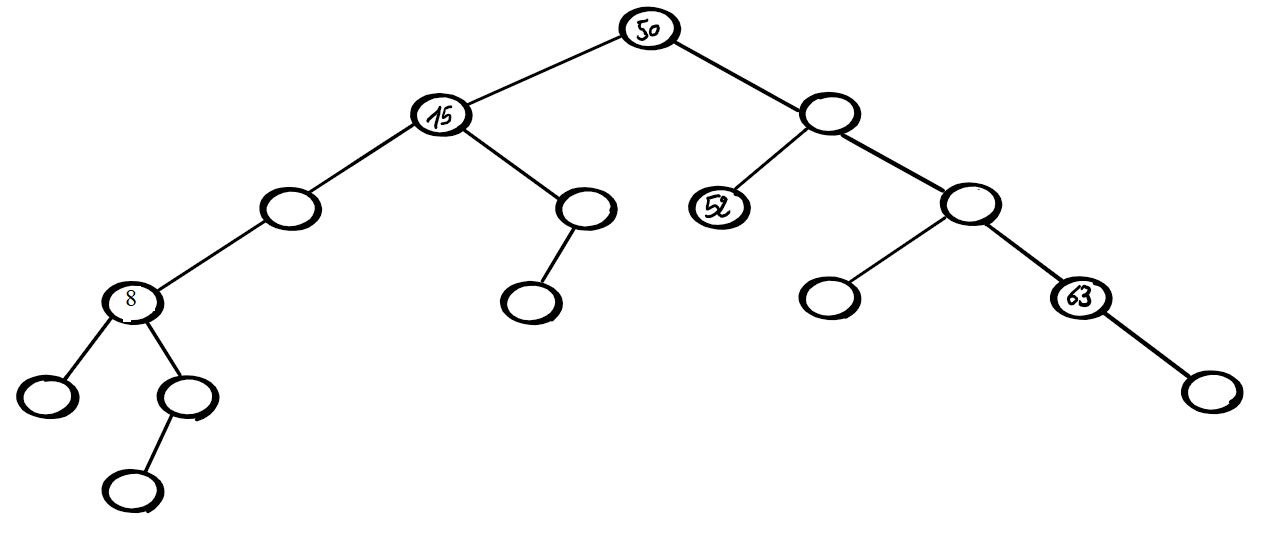
Un étiquetage intéressant d'un arbre de recherche est le suivant :

La racine est étiquetée 1.
La premier nœud du sous arbre gauche prend l'étiquette de son père auquel on ajoute un 0.
La premier nœud du sous arbre droit prend l'étiquette de son père auquel on ajoute un 1.

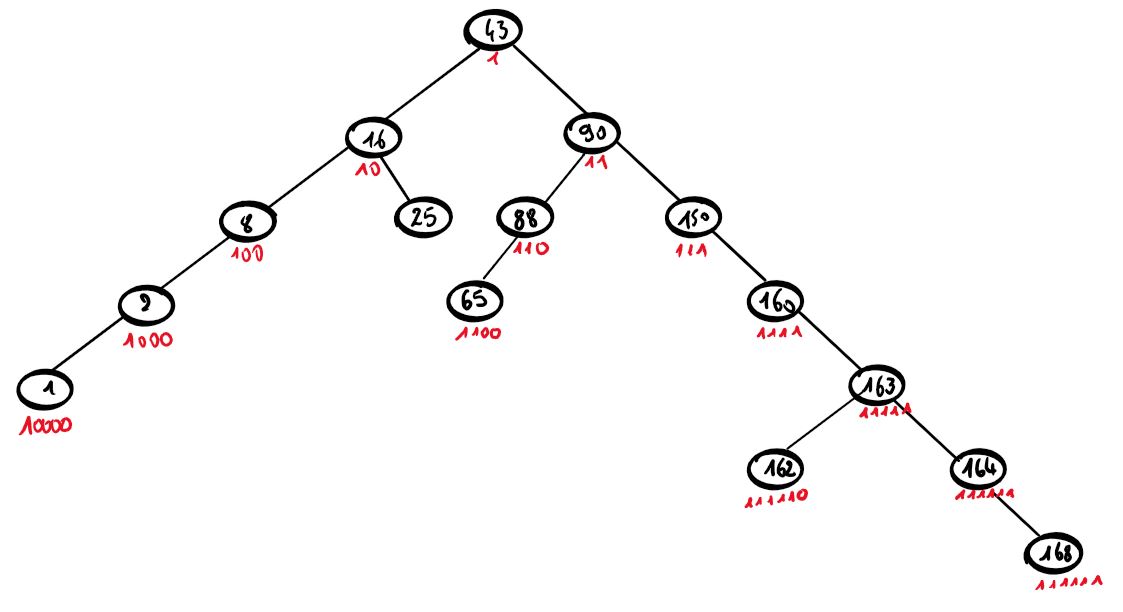
Quelle est l'étiquette de 25 dans l'arbre précédent ?

Étiqueter comme l'exemple précédent l'arbre suivant :

On observe que les étiquettes des nœuds de profondeur p sont constituées de p + 1 bits, et sont deux à deux distinctes. On en déduit que toutes les étiquettes des nœuds d'un même arbre sont deux à deux distinctes.

Les étiquettes peuvent être vues comme les écritures de numéros en base 2 : on a ainsi numéroté les différents nœuds de l'arbre.

Pour la propriété suivante vous devez connaître deux notations mathématiques :

La notation $\lfloor x \rfloor$ désigne la partie entière.
- $\lfloor 1,1 \rfloor=1$.
- $\lfloor 2,8 \rfloor=2$.
- $\lfloor -1,1 \rfloor=-2$.
La fonction $log_2$ est une fonction définie sur $]0;+\infty[$ par $log_2(x)=\frac{ln(x)}{ln(2)}$. Elle se nomme logarithme en base 2.

Un résultat à retenir pour la suite : $log_2(2^n)=n$

Nous aurons l'occasion de réutiliser cette fonction dans le cours A3

Pour un arbre binaire de recherche de hauteur $h$ et de taille $n$ les inégalités : $$\lfloor \log_2(n)\rfloor \leq h\leq n-1$$

Pour démontrer ce résultat nous allons observer le cas où l'arbre est le plus profond et le cas où l'arbre est le moins profond.

Cas où l'arbre est le plus profond :

Pour une taille $n$ fixée, la hauteur maximale d’un arbre binaire est $h = n − 1$, qu’on obtient avec des arbres « filiformes » comme cet arbre :

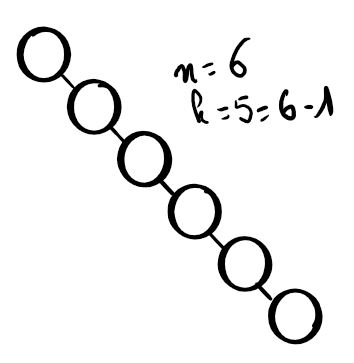
Ainsi $h\leq n-1$.
Cas où l'arbre est le moins profond

Les arbres de taille $n$ de hauteur minimale sont les arbres comme ces arbres :

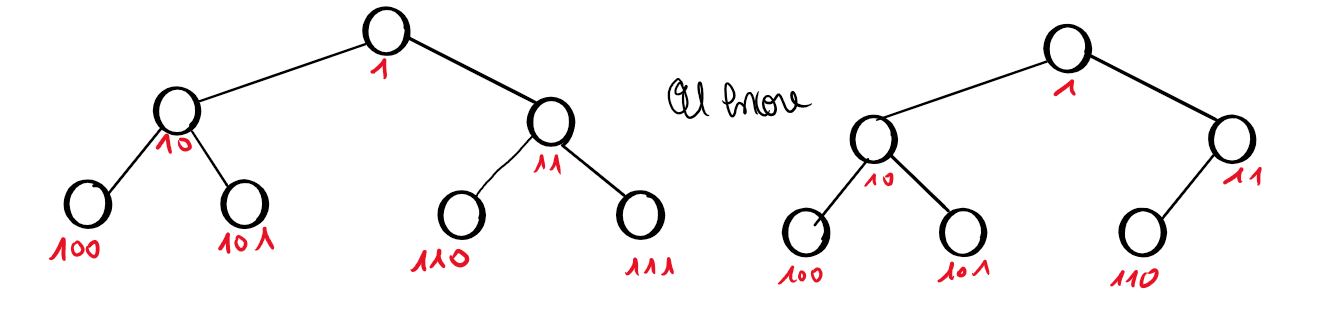
les clés des feuilles sont supérieures ou égales en binaire à $100...0$ où 0 est répété $p$ fois

Dans ce cas la hauteur $h$ est égale à $p$, il y a au moins $n=2^p$ nœuds

Or $log_2(2^p)=p$

Ainsi $log_2(n)\leq h$

Vérifions cette inégalité sur cet arbre :

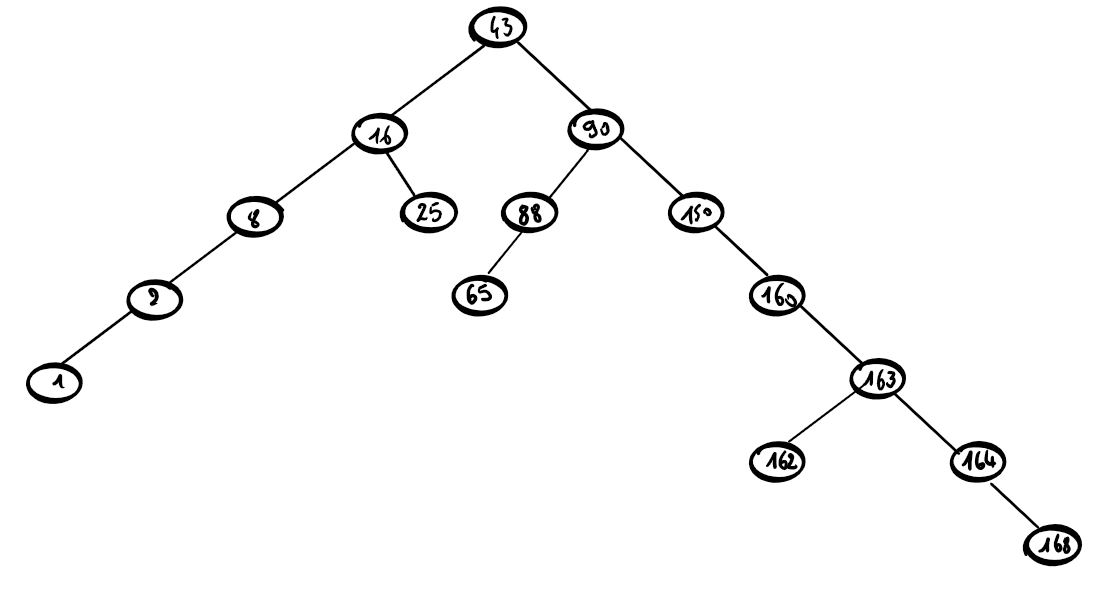
La taille de cet arbre est 15.

La hauteur est 6.

$log_2(15)=3,9$ à $10^{-1}$ près.

$\lfloor 3,9 \rfloor=3$

On a bien : $3\leq 6 \leq 14$

Vérifier l'exactitude de l'inégalité sur cet arbre:

Une implémentation de l'objet arbre binaire de recherche en Python

La classe arbre binaire de recherche (ABR) avec Python

class ABR:

    def __init__(self, valeur, fg=None, fd=None):
        self.v = valeur
        self.fg = fg
        self.fd = fd

    def ajoute(self, valeur):
        if self == None:
            return ABR(valeur, None, None)
        elif valeur < self.v:
            return ABR(self.v, ABR.ajoute(self.fg,valeur), self.fd)
        else:
            return ABR(self.v, self.fg, ABR.ajoute(self.fd, valeur))

    def affiche(self):
        if self == None:
            return None
        else :
            return [self.v, ABR.affiche(self.fg), ABR.affiche(self.fd)]

# À tester pour exemple
arbre = ABR(25).ajoute(17).ajoute(32).ajoute(5)
arbre.affiche()
# Utiliser l'affichage pour faire une représentation de l'arbre

Implémenter,avec cette implémentation, l'arbre suivant :

Écrire en Python une méthode taille qui renvoie la taille d'un arbre binaire.

Vous pouvez vous aider de la relation du cours accessible ici.

Écrire en Python une méthode hauteur qui renvoie la hauteur d'un arbre binaire.

Pour vous aider, chercher une méthode récursive assez simple qui utilise la fonction max et utilise la structure récursive des arbres binaires.

Exercices du baccalauréat

Cet exercice porte sur les arbres binaires de recherche.

Dans cet exercice, les arbres binaires de recherche ne peuvent pas comporter plusieurs fois la même clé. De plus, un arbre binaire de recherche limité à un nœud a une hauteur de 1.

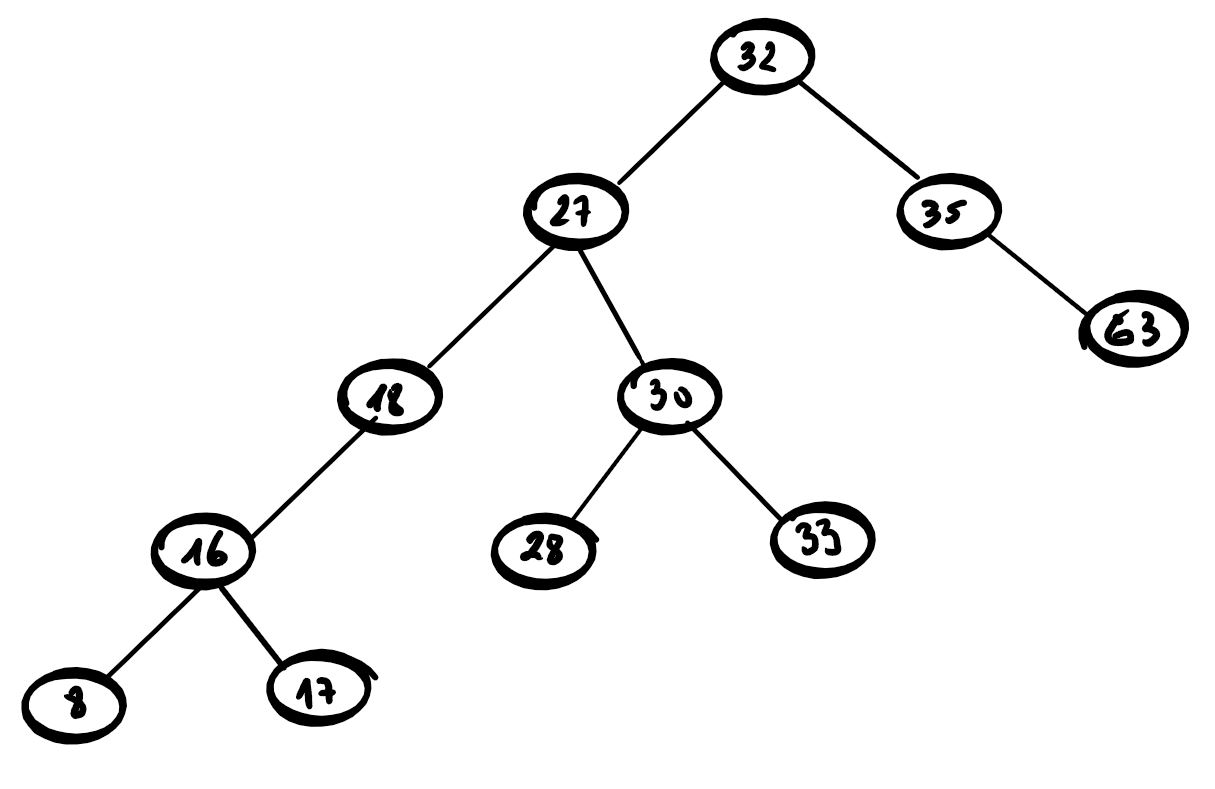
On considère l'arbre binaire de recherche représenté ci-dessous, où val représente un entier :

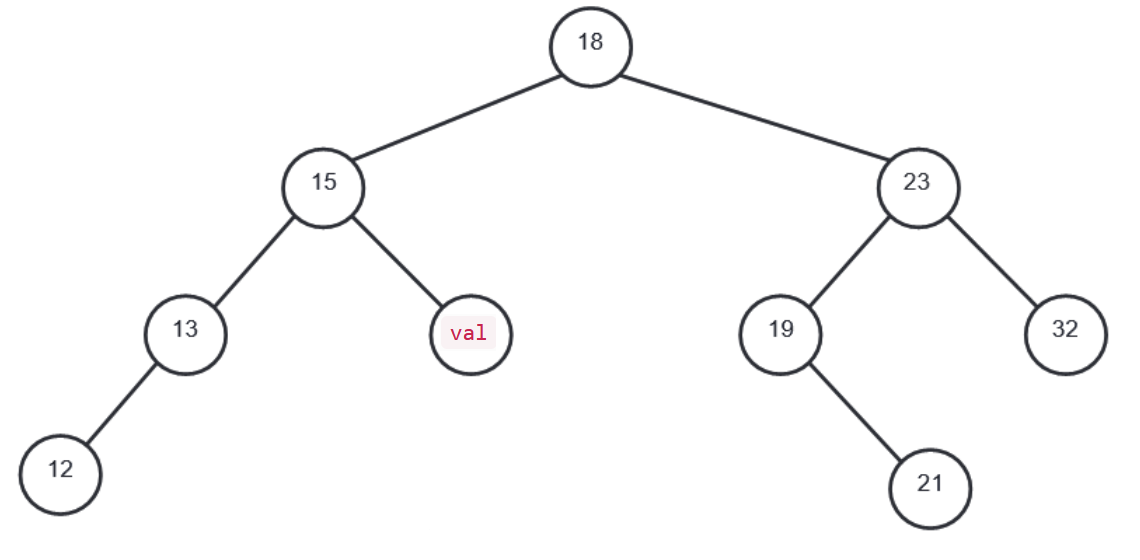
1. Donner le nombre de feuilles de cet arbre et préciser leur valeur (c'est-à-dire leur étiquette).
2. Donner le sous arbre-gauche du nœud 23.
3. Donner la hauteur et la taille de l’arbre.
4. Donner les valeurs entières possibles de val pour cet arbre binaire de recherche.

On suppose, pour la suite de cet exercice, que val est égal à 16.

On considère la classe Noeud définie de la façon suivante en Python :

class Noeud:
    def __init__(self, v):
        self.ag = None
        self.ad = None
        self.v = v

    def insere(self, v):
        n = self
        est_insere = False
        while not est_insere :
            if v == n.v:
                # début du bloc 1
                est_insere = True
                # fin du bloc 1
            elif v < n.v:
                # début du bloc 2
                if n.ag != None:
                    n = n.ag
                else:
                    n.ag = Noeud(v)
                    est_insere = True
                # fin du bloc 2
            else:
                # début du bloc 3
                if n.ad != None:
                    n = n.ad
                else:
                    n.ad = Noeud(v)
                    est_insere = True
                # fin du bloc 3

    def insere_tout(self, vals):
        for v in vals:
            self.insere(v)

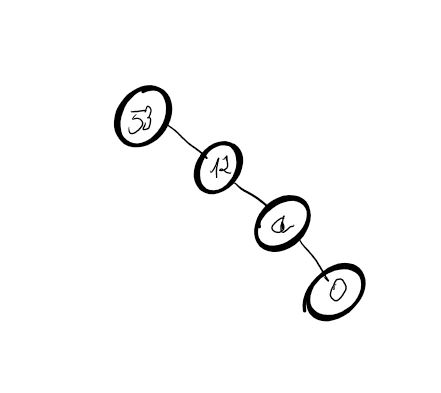
Représenter l'arbre construit suite à l’exécution de l’instruction suivante :
```
racine = Noeud(18) 
racine.insere_tout([12, 13, 15, 16, 19, 21, 32, 23])
```
Écrire les deux instructions permettant de construire l’arbre de la figure précédente. On rappelle que le nombre val est égal à 16.
On considère l’arbre tel qu’il est présenté sur la figure précédente. Déterminer l’ordre d’exécution des blocs (repérés de 1 à 3) suite à l’application de la méthode insere(19) au nœud racine de cet arbre.

Écrire une méthode recherche(self, v) qui prend en argument un entier v et renvoie la valeur True si cet entier est une étiquette de l'arbre, False sinon.

Renforcement

On donne l'arbre $B$ suivant :

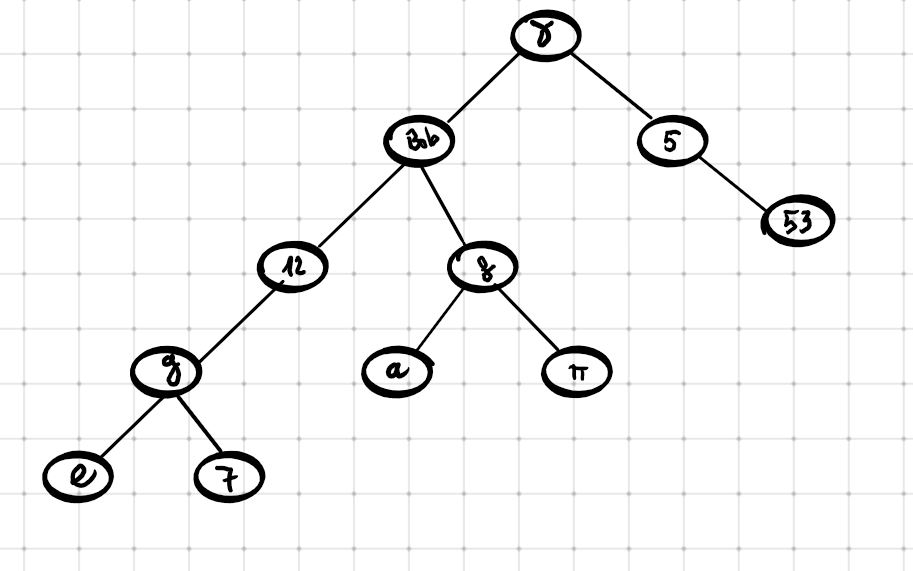
Déterminer :

la racine,
le nombre de feuilles,
le nombre de branches,
l'arité,
sa taille $T(B)$,
La hauteur de $B$, $H(B)$,
$LC(B)$,
$LCE(B)$,
$LCI(B)$,
$PM(B)$,
$PME(B)$,
$PMI(B)$.

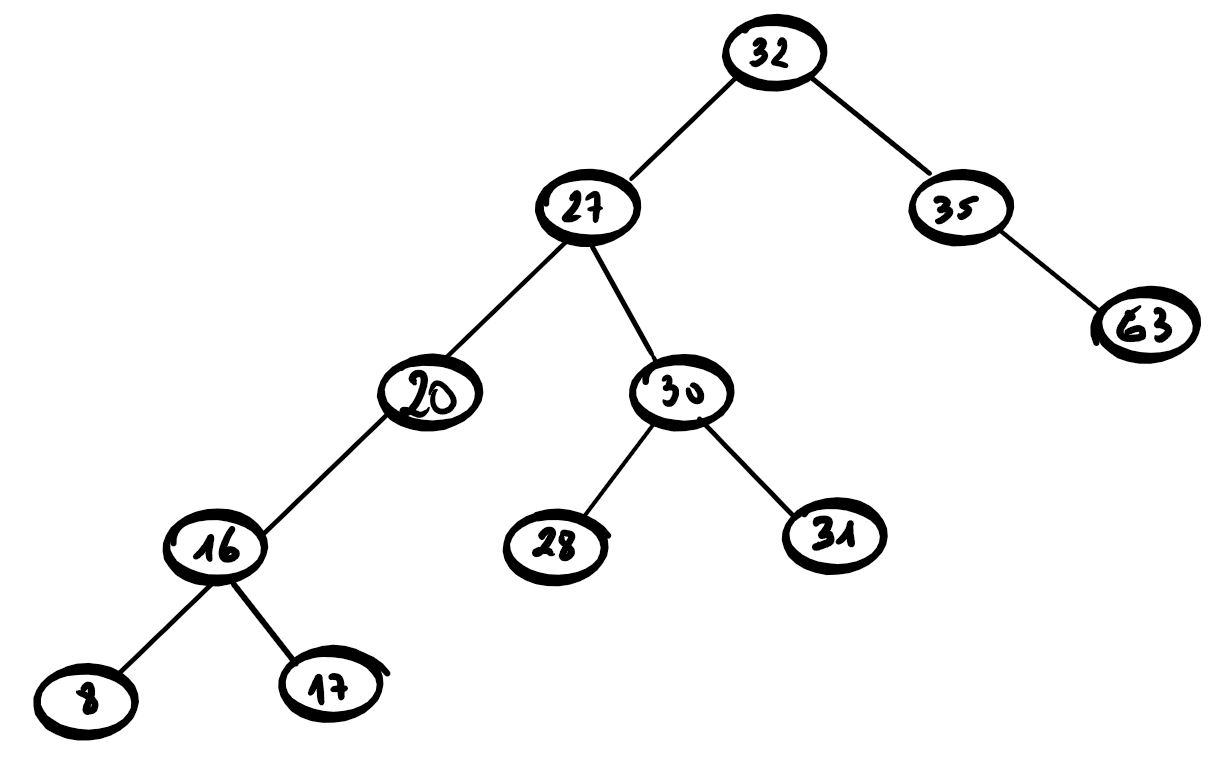
Compléter cet arbre pour que ce soit un arbre binaire de recherche :

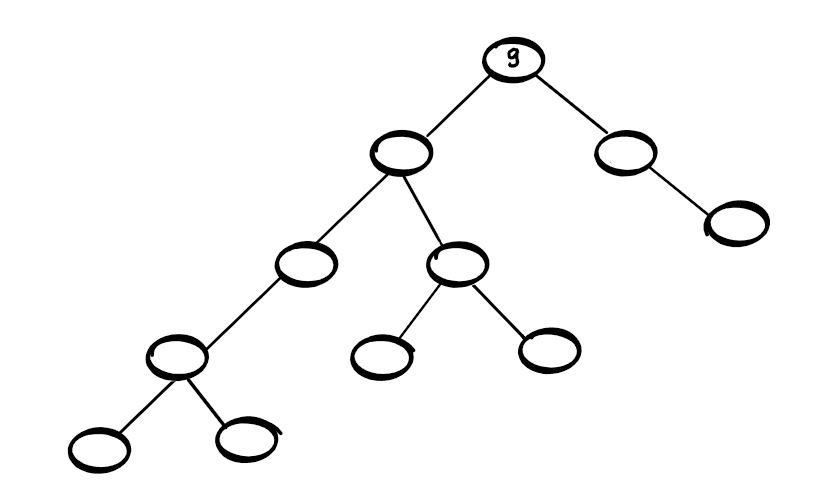
Savoir faire et Savoir

Évaluer quelques mesures sur les arbres,
Construire à la main un arbre binaire de recherche,
Étiqueter un arbre binaire de recherche,
Implémenter un arbre binaire de recherche en Python,
Rajouter des méthodes, des fonctions à une implémentation d'un arbre binaire de recherche en Python.
Identifier des situations nécessitant une structure de données arborescente.

Le vocabulaire sur les arbres,
Qu'un arbre est une structure hiérarchique et non linéaire.

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲