Demander le programme !
- définir une fonciton continue
- Le TVI et son corollaire
- la détermination de l'ensemble sur lequel une fonciton est continue
- le repérage des cas d'applications du corollaire du TVI
- le lien entre corollaire du TVI et les solutions d'une équaiton.
Notion de continuité
Soit $f$ une fonction définie sur un intervalle $I$ et $a\in I$.
- On dit que $f$ est continue en $a$ si $\lim\limits_{x \to a^-} f(x)=f(a)=\lim\limits_{x \to a^+}
f(x)$.
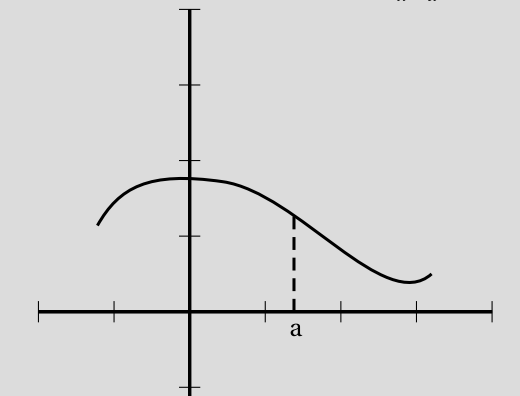
- On dit que $f$ est continue à gauche de $a$ si $\lim\limits_{x \to a^{-}} f(x)=f(a)$.
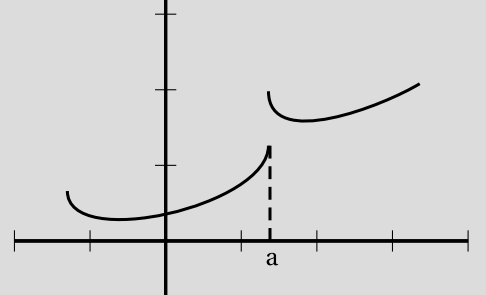
- On dit que $f$ est continue à droite de $a$ si $\lim\limits_{x \to a^{+}} f(x)=f(a)$.
On dit que $f$ est continue sur $I$ si $f$ est continue en $a$ quelque soit la valeur de $a$ dans I.
Autrement dit, $f$ est continue sur $I$ si la courbe représentative de $f$ se trace sans lever le crayon.
Continuité des fonctions usuelles
- Les fonctions polynôme, rationnelles, valeur absolue et racine carrée sont continues sur les intervalles où elles sont définies.
- La somme, le produit , le quotient et la composée de fonctions continues sont continues.
Donner pour chaque fonction l'ensemble sur lequel elles sont continues.
- $f_1: x \longmapsto x^2-5x+1$
- $f_2: x \longmapsto \sqrt{1+x}$
- $f_3: x \longmapsto \frac{\sqrt{x}+1}{\sqrt{|x|+2}}$
Théorème des valeurs intermédiaires
T.V.I.
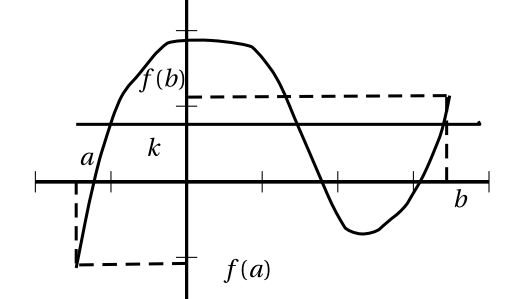
Si $f$ est une fonction continue sur un intervalle $[a;b]$, alors pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe au moins un réel $c$ de $[a;b]$ tel que $f(c)=k$.
Autrement dit l'équation $f(x)=k$ admet au moins une solution sur $[a;b]$.
Montrer que l'équation $2x^3+3x^2-2x=2$ admet au moins une solution sur $[-2;1]$
Corollaire du théorème des valeurs intermédiaires
Si $f$ est une fonction continue et strictement monotone sur $[a;b]$, alors pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe un unique réel $c\in[a;b]$ tel que $f(c)=k$.
Autrement dit, l'équation $f(x)=k$ a une unique solution sur $[a;b]$
Existence :
La fonction $f$ est continue sur $[a;b]$. D'après le T.V.I., pour tout réel $k$ compris entre $f(a)$ et $f(b)$, l'équation $f(x)=k$ admet au moins une solution $c\in[a;b]$.
Unicité : Supposons qu'il existe au moins deux solutions $c$ et $c'$ à $f(x)=k$.
1er cas :$c<c'$ alors la strictement croissance de $f$ impose $f(c)<f(c')$ c'est à dire $k<k$
2ième cas : $c'<c$ alors la strictement croissance de $f$ impose $f(c')<f(c)$ c'est à dire $k<k$</p>
Les deux cas donne une conclusion erronée ce qui contredit l'existence de $c'$ et assure l'unicité de $c$.
Montrer que l'équation $x^3+x=1$ admet une unique solution $\alpha$ sur $[0;1]$.
Donner un encadrement de $\alpha$ d'amplitude $10^{-2}$.
Exercices
Montrer que chaque équation admet une unique solution sur $I$ et donné un encadrement de la solution à $10^{-2}$ près.
- $x^3+x^2=5$ et $I=[1;2]$
- $\sqrt{1+2x}=x$ et $I=[0;5]$
- $\frac{x-1}{1+x^2}=x$ et $I=\mathbb{R}$
Vrai ou Faux
Soit $f$ une fonction définie sur un intervalle $I$.
- Si $f$ change de signe sur $I$, alors $f$ s'annule sur $I$.
- Si $I=[a;b]$, $f(a)f(b)>0$ et $f$ continue sur $I$, alors $f$ ne s'annule pas sur $I$.
- Si $f$ s'annule une seule fois sur $I$ et $f$ continue sur $I$, alors $f$ est strictement monotone sur $I$.
QCM
Soit $f$ une fonction définie et continue sur $[-2;3]$ telle que $f(-2)=0$ et $f(3)=7$.
- Le nombre de solutions de l'équation $f(x)=4$ sur $[-2;3]$ est :
- zéro
- une exactement
- au moins une
- on ne peut pas savoir
- Même question avec l'équation $f(x)=10$ :
- zéro
- une exactement
- au moins une
- on ne peut pas savoir
- On suppose de plus que $f$ est strictement croissante .
Le nombre de solutions de l'équation $f(x)=4$ sur $[-2;3]$ est :
- zéro
- une exactement
- au moins une
- on ne peut pas savoir
- Même question avec l'équation $f(x)=10$ :
- zéro
- une exactement
- au moins une
- on ne peut pas savoir

Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.