Demander le programme !

  1. la définition d'une propabilité
  2. les définition d'intersection , d'union , de complémentaire
  3. les formules de premières sur les probabilités
  4. la définition d'une probabilité conditionnelle
  5. la formule des probabilités totales
  6. définir l'indépendance de deux événements
  1. un arbre pondéré
  2. l'interprétation d'un événement en terme de probabilité conditionnelle
  3. la mobilisation de ses savoirs sur les suites pour résoudre un problème de probabilités

Forme algébrique d'un nombre complexe.

Définitions générales.

  • Un nombre complexe est un élément de la forme $x+iy$ , où $x$ et $y$ sont des réels et $i$ un nombre vérifiant $i^2=-1$. L'ensemble des nombres complexes est noté $\mathbb{C}$.

    • $2+3i;~i+1,5;~2;~-4i;~\pi+\sqrt2i$ sont des nombres complexes.

    L'écriture $x+iy$, où $x\in\mathbb{R} \textrm{ et } y\in\mathbb{R}$, d'un nombre complexe $z$ est la forme algébrique d'un complexe.

    Opérations sur les nombres complexes

    Soient deux nombres complexes $z$ et $z'$ de formes algébriques $x+iy$ et $x'+iy'$.

    Effectuer les calculs suivants :

    $2+3i-(3-5i)$

    $(1+i)(2-\frac12i)$

    Inverse

    Soit $z$ un nombre complexe de forme algébrique $x+iy$.

    Si $z\neq 0$ alors : $\frac1z=\frac{x}{x^2+y^2}+i\frac{-y}{x^2+y^2}$.

    Effectuer le calcul suivant :

    $\frac{1}{-1+3i}$

    Quotient

    Soit $z$ et $z'$ deux complexes de forme algébrique $x+iy$ et $x'+iy'$.

    Si $z'\neq 0$ alors : $\frac{z}{z'}=z\times\frac1{z'}$.

    Effectuer le calcul suivant :

    $\frac{3+2i}{1-i}$

    $zz'=0$ si et seulement si $z=0$ ou $z'=0$.

    Résoudre l'équation suivante :

    $(z-2)(2z-1+i)=0$

    Partie imaginaire et partie réelle d'un nombre complexe

    Partie réelle et partie imaginaire

    Soit $z$ un complexe de forme algébrique $x+iy$.

    Alors $x$ est la partie réelle de $z$ notée $Re(z)$, $y$ la partie imaginaire de $z$ notée $Im(z)$.

    Déterminer les partie réelle et imaginaire des complexes suivants :

    1. $z_1=5+2i$
    2. $z_2=2-8i$
    3. $z_3=3$
    4. $z_4=-2i$

    Imaginaire pur

    Un nombre complexe de forme algébrique $iy$ avec $y\in\mathbb{R}$ est appelé imaginaire pur.

    1. $z$ est un réel si et seulement si $Im(z)=0$.
    2. $z$ est un imaginaire pur si et seulement si $Re(z)=0$.
    3. $z=0$ si et seulement si $Re(z)=0$ et $Im(z)=0$.
    4. $z=z'$ si et seulement si $Re(z)=Re(z')$ et $Im(z)=Im(z')$.

    Autrement dit : deux complexes sont égaux si et seulement si leurs parties réelles et imaginaires sont égales.

    Ces 4 propriétés découlent directement de l'unicité de la forme algébrique d'un nombre complexe.

    Prenons par exemple la 4 :

    On note $x+iy$ et $x'+iy'$ les formes algébriques des nombres complexes $z$ et $z'$ respectivement.

    $\Leftarrow$: Si $Re(z)=Re(z')$ et $Im(z)=Im(z')$ alors $x=x'$ et $y=y'$ ainsi $z=x+iy=x'+iy'=z'$.

    $\Rightarrow$: Si $z=z'$ alors d'aprés l'unicité de la forme algébrique d'un nombre complexe $x=x'$ et $y=y'$ donc $Re(z)=0$ et $Im(z)=0$.

    Résoudre l'équation $2z-3i=(z-5)(1+i)$.

    Conjugué d'un nombre complexe

    Nombre conjugué

    On appelle nombre conjugué du nombre complexe $z=x+iy$ le nombre complexe noté $\overline{z}$ de forme algébrique $x-iy$.

    Donnez les conjugué des complexes suivants :

    1. $z_1=-5-i$
    2. $z_2=2-3i$

    L'inverse d'un complexe non nul z est $\frac1{z}=\frac{\overline{z}}{z\overline{z}}$.

    $z+\overline{z}=2Re(z)$ et $z-\overline{z}=2iIm(z)$.

    Soit $z$ un nombre complexe.

    $z+\overline{z}=Re(z)+iIm(z)+Re(z)-iIm(z)=2Re(z)$

    $z-\overline{z}=Re(z)+iIm(z)-Re(z)+iIm(z)=2iIm(z)$

    Pour tous nombres complexes $z$ et $z'$ et pour tout entier naturel $n$.

    1. $z$ est réel si et seulement si $\overline{z}=z$.
    2. $z$ est imaginaire pur si et seulement si $\overline{z}=-z$.
    3. $\overline{z+z'}=\overline{z}+\overline{z'}$.
    4. $\overline{zz'}=\overline{z}\overline{z'}$.
    5. $\overline{z^n}=\overline{z}^n$.
    6. Si $z'\ne 0$ alors $\overline{\frac1{z'}}=\frac1{\overline{z'}}$ et $\overline{(\frac{z}{z'})}=\frac{\overline{z}}{\overline{z'}}$.
    7. $\overline{overline{z}}=z$

    Toutes ces propriétés se démontrent à l'aide de la forme algébrique.

    1. (sens direct) On suppose que $z$ est un réel : $z=Re(z)$. Alors $Im(z)=0$ et donc $\overline{z}=Re(z)+i\times 0=Re(z)=z$.

      (sens réciproque) On suppose que $z=\overline{z}$ donc $Re(z)+iIm(z)=Re(z)-iIm(z)$ et par unicité de la forme algébrique d'un complexe, on en déduit donc $Re(z)=Re(z)$ et $Im(z)=-Im(z)$. D'où $Im(z)=0$ : $z$ est un réel.

    2. De la même manière que ci-dessus.
    3. $\overline{z+z'}=Re(z+z')-iIm(z+z')=Re(z)+Re(z')-iIm(z)-iIm(z')=(Re(z)-iIm(z))+(Re(z')-iIm(z'))=\overline{z}+\overline{z'}$

    4. $\overline{zz'}=Re(zz')-iIm(zz')=Re(z)Re(z')-Im(z)Im(z')-i(Re(z)Im(z')+Re(z')Im(z))$

      $\overline{z}\overline{z'}=(Re(z)-iIm(z))(Re(z')-iIm(z'))=Re(z)Re(z')-Im(z)Im(z')+i(-Re(z)Im(z')-Re(z')Im(z))=\overline{zz'}$

    5. Récurrence à faire pour le plaisir.

    6. Soit $z$ un complexe non nul.

      $\overline{(\frac1{z})}\times \overline{z}=_{(4)} \overline{\frac1{z}\times z}=\overline{1}=1$.

      Ainsi $\overline{(\frac1{z})}\times \overline{z}=1$ et $\overline{(\frac1{z})}=\frac1{\overline{z}}$.

      En outre, si $z'\neq0$, $\overline{(\frac{z}{z'})}=\overline{z\times\frac1{z'}}=_{(4)} \overline{z}\times

      En outre, si $z'\neq0$, $\overline{(\frac{z}{z'})}=\overline{z\times\frac1{z'}}=_{(4)} \overline{z}\times\overline{\frac1{z'}}=_{\textrm{d'après ci-dessus}}\overline{z}\times \frac1{\overline{z'}}=\dfrac{\overline{z}}{\overline{z'}}$

    Représentation géométrique d'un nombre complexe.

    Le plan est muni d'un repère orthonormal direct $(O,\overrightarrow{u};\overrightarrow{v})$.

    Soit $z$ un nombre complexe de forme algébrique $x+iy$ , où $x$ et $y$ sont des réels.

    Point image associé à un complexe

    À tout nombre complexe , $z=x+iy$ est associé le point M du plan de coordonnées $(x ; y)$ , appelé point image de $z$ noté $M(z)$.

    affixe d'un point

    À tout point $M$ du plan de coordonnées $(x ; y)$ est associé le complexe $z=x+iy$ appelé affixe du point M.

    Représenter les points images $A$, $B$, $C$ et $D$ d'affixes $z_A=3+i$, $z_B=-3i$, $z_C=-1$, $z_D=-2+1,5i$.

    Les points d'affixes $z$ et $\overline{z}$ sont symétriques par rapport à l'axe des abscisses.

    Les points d'affixes $z$ et $-z$ sont symétriques par rapport à l'origine $O$

    Affixes et géométrie

    À tout vecteur du plan $\overrightarrow{u}$ de coordonnées $(x;y)$, on associe le nombre complexe $x+iy$ appelé affixe du vecteur $\overrightarrow{u}$.

    Réciproquement à tout nombre complexe de forme algébrique $x+iy$ , on associe le vecteur de coordonnées $(x;y)$.

    Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ d'affixes respectives $z_{\overrightarrow{u}}$ et $z_{\overrightarrow{v}}$.

    1. Si $z_{\overrightarrow{u}}=x+iy$ alors $\overrightarrow{u}$ a pour norme $\sqrt{x^2+y^2}$.
    2. L'affixe du vecteur $\overrightarrow{u}+\overrightarrow{v}$ est $z_{\overrightarrow{u}}+z_{\overrightarrow{v}}$.
    3. Si $k$ est un réel , l'affixe du vecteur $k{\overrightarrow{u}}$ est $kz_{\overrightarrow{u}}$.

    Soit deux points du plan d'affixes $z_A$ et $z_B$.

    1. L'affixe du vecteur $\overrightarrow{AB}$ est $z_B-z_A$.
    2. L'affixe du milieu I de $[AB]$ est $z_I=\frac12(z_A+z_B)$.

    Pour démontrer ces propriétés , il faut avoir bien compris le lien entre coordonnées d'un objet géométrique et la forme algébrique d'un nombre complexe.

    Les coordonnées du vecteur $\overrightarrow{AB}$ sont $(x_B-x_A ; y_B-y_A)$ ainsi l'affixe de ce vecteur est $$x_B-x_A+i(y_B-y_A)=x_B+iy_B-(x_A+iy_A)=z_B-z_A$$

    Démontrer le deuxième point de la propriété précédente.

    Equations du second degré

    Soit l'équation $az^2+bz+c=0$, d'inconnue $z$, où $a$ et $b$ sont des réels avec $a\neq 0$.

    Le discriminant de cette équation du second degré est $\Delta=b^2-4ac$.

    Pour tout nombre complexe $z$ , $az^2+bz+c=a(z-z_1)(z-z_2)$

    Soit $z$ un nombre complexe.

    $az^2+bz+c=a(z^2+\frac{b}{a}z+\frac{c}{a})=a((z+\frac{b}{2a})^2-\frac{b^2}{4a^2}+\frac{c}{a})=a((z+\frac{b}{2a})^2-\frac{b^2-4ac}{4a^2})=a((z+\frac{b}{2a})^2-\Delta)$.

    Résoudre l'équation : $z^2+3z+4=0$.

    Forme trigonométrique d'un nombre complexe non nul.

    On munit le plan complexe d'un repère orthonormé $(O; \overrightarrow{u},\overrightarrow{v})$.

    Argument d'un nombre complexe non nul.

    Pour tout M distinct de O, on peut donner les coordonnées cartésiennes $(x ; y)$ ou les coordonnées polaires $(r;\theta)$ avec $r=OM$ et $\theta=(\overrightarrow{u};\overrightarrow{OM})$ à $2k\pi$ près $(k\in\mathbb{Z})$.

    Soit $z$ un nombre complexe non nul, M le point d'affixe $z$ et $(r;\theta)$ un couple de coordonnées polaires de M. Alors :

    Soit $z$ un nombre complexe non nul, M le point d'affixe $z$ et $(r;\theta)$ un couple de coordonnées polaires de M.

    La longueur $OM$ est appelelé module de $z$ est on a $OM=|z|=\sqrt{x^2+y^2}$

    L'angle $\theta=(\overrightarrow{u},\overrightarrow{OM})[p\pi]$ est appelé argument de $z$. On a $\cos(\theta )=\frac{x}{r}$ et $\sin(\theta )=\frac{y}{r}$

    Déterminer le module et un argument du nombre complexe de forme algébrique $3-3i$.

    Pour tout complexe $z$ non nul :

    1. $|z|=|\overline{z}|=|-z|=|-\overline{z}|$
    2. $arg(\overline{z})=-arg(z)~[2\pi]$
    3. $arg(-z)=\pi+arg(z)~[2\pi]$
    4. $arg(-\overline{z})=\pi-arg(z)~[2\pi]$

    On considère les points $M_1$ , $M_2$ , $M_3$ , $M_4$ d'affixes respectives : $z,\overline{z},-z,-\overline{z}$.

    1. Comme $OM_1=OM_2=OM_3=OM_4$ on a $|z|=|\overline{z}|=|-z|=|-\overline{z}|$
    2. Dans la suite on note $\theta$ un argument de z.

      Si $z=x+iy$ alors $\overline{z}=x-iy$ donc si $\theta'$ est argument de $\overline{z}$ alors $sin(\theta')=-\frac{y}{r}=-sin(\theta)=sin(-\theta)$ et $cos(\theta')=\frac{x}{r}=cos(\theta)=cos(-\theta)$. Ainsi on a $\theta'=-\theta$ à $2\pi$ près.

    3. Si $z=x+iy$ alors $-z=-x-iy$ donc si $\theta'$ est argument de $-z$ alors $cos(\theta')=-\frac{x}{r}=-cos(\theta)=cos(\pi+\theta)$ et $sin(\theta')=-\frac{y}{r}=-sin(\theta)=sin(\pi+\theta)$. Ainsi on a $\theta'=\pi+\theta$ à $2\pi$ près.
    4. Si $z=x+iy$ alors $-\overline{z}=-x+iy$ donc si $\theta'$ est argument de $-\overline{z}$ alors $cos(\theta')=-\frac{x}{r}=-cos(\theta)=cos(\pi-\theta)$ et $sin(\theta')=\frac{y}{r}=sin(\theta)=sin(\pi-\theta)$. Ainsi on a $\theta'=\pi-\theta$ à $2\pi$ près.

    Dans un repère placer un point d'affixe $z$ et placer les points d'affixes $\overline{z}$, $-z$, $-\overline{z}$

    Forme trigonométrique d'un nombre complexe non nul

    Pour tout nombre complexe de forme algébrique $x+iy$ , on a $r=\sqrt{x^2+y^2}>0$ , donc $z=r(\frac{x}{r}+\frac{y}{r})=r(\cos(\theta)+\sin(\theta))$.

    Forme trigonométrique

    Soit $z$ un nombre complexe non nul. L'écriture $z=r(\cos(\theta)+i\sin(\theta))$ , avec $r=|z|$ et $\theta=arg(z)~[2\pi]$, est appelé forme trigonométrique.

    Donner la forme trigonométrique dans chacun des cas suivants:

    1. $3-3i$.
    2. $3\sqrt{2}(\cos(\frac{\pi}4)-i\sin(\frac{\pi}4))$
    3. $-2(\cos(\frac{\pi}{3})+i\sin(\frac{\pi}{3})$

    Les complexes $z=r(\cos(\theta)+i\sin(\theta))$ et $z'=r(\cos(\theta')+i\sin(\theta'))$ , avec $r>0$ et $r'>0$ , sont égaux si et seulement si : $r=r'$ et $\theta=\theta'+2k\pi , k\in\mathbb{Z}$.

    $\Leftarrow$ C'est immédiat.

    $\Rightarrow$ Si $z=z'$ alors si les formes algébriques de$z$ et $z'$ sont respectivement $x+iy$ et $x'+iy'$, on a $x=x'$ et $y=y'$. Ainsi $r=\sqrt{x^2+y^2}=\sqrt{x'^2+y'^2}=r'$.

    D'autre part on a $r\cos(\theta)=r'cos(\theta')$ et $r\sin(\theta)=r'\sin(\theta')$ d'où $\cos(\theta)=\cos(\theta')$ et $\sin(\theta)=\sin(\theta')$

    Ainsi $\theta=\theta'~[2\pi]$.

    Soit $z=r(\cos(\theta)+i\sin(\theta))$ et $z'=r'(\cos(\theta')+i\sin(\theta'))$ deux nombres complexes.

    1. $zz'=rr'(\cos(\theta+\theta')+i\sin(\theta+\theta'))$
    2. $\frac1{z'}=\frac1{r'}(\cos(-\theta')+i\sin(-\theta'))$ et $\frac{z}{z'}=\frac{r}{r'}(\cos(\theta-\theta')+i\sin(\theta-\theta'))$.
    1. $zz'=r(\cos(\theta)+i(\sin(\theta))\times r'(\cos(\theta')+i(\sin(\theta'))=rr'(\cos(\theta)\cos(\theta')-\sin(\theta)\sin(\theta')+i(\cos(\theta)\sin(\theta')+\cos(\theta')\sin(\theta)))=rr'(\cos(\theta+\theta')+i\sin(\theta+\theta'))$.
    2. $\frac1{z'}=\frac{\overline{z'}}{{r'}^2}=\frac{r'(\cos(-\theta')+i\sin(-\theta'))}{r'^2}=\frac1{r'}(\cos(-\theta')+i\sin(-\theta'))$ et $\frac{z}{z'}=\frac{z\overline{z'}}{r'^2}=\frac{rr'(\cos(\theta-\theta')+i\sin(\theta-\theta'))}{r'^2}=\frac{r}{r'}(\cos(\theta-\theta')+i\sin(\theta-\theta'))$.

    Module :

    1. $|zz'|=|z|\times|z'|$
    2. $|z^n|=|z|^n$ ; $n\in\mathbb{Z}$
    3. $|\frac1{z}|=\frac1{|z|}$ avec $z\ne0$
    4. $|\frac{z}{z'}|=\frac{|z|}{|z'|}$ avec $z'\ne0$.

    Argument :

    1. $arg(zz')=arg(z)+arg(z')~[2\pi]$
    2. $arg(z^n)=n arg(z)~[2\pi]$
    3. $arg(\frac1{z})=-arg(z)~[2\pi]$
    4. $arg(\frac{z}{z'})=arg(z)-arg(z')~[2\pi]$.

    Déterminer la forme trigonométrique des complexes suivants :

    1. $-1+i$
    2. $1-i\sqrt{3}$
    3. $(-1+i)(1-i\sqrt{3})$
    4. $\frac{-1+i}{1-i\sqrt{3}}$

    Module, argument et géométrie

    Soit $\overrightarrow{a}$ un vecteur d'affixe $z$. Alors $||\overrightarrow{a}||=|z|$ et $(\overrightarrow{u};\overrightarrow{a})=arg(z)~[2\pi]$

    Soit $A$ le point tel que $\overrightarrow{OA}=\overrightarrow{a}$. Alors A a pour affixe $z$.

    En outre $||\overrightarrow{a}||=OA=|z|$ et $(\overrightarrow{u};\overrightarrow{a})=(\overrightarrow{u};\overrightarrow{OA})=arg(z)~[2\pi]$ d'où les résultats.

    $z_A$ , $z_B$ , $z_C$ et $z_D$ sont quatre complexes distincts , d'images A , B , C et D dans le plan complexe.

    1. $|z_B-z_A|=AB$ et $arg(z_B-z_A)=(\overrightarrow{u} ; \overrightarrow{AB})$.
    2. $|\frac{z_B-z_D}{z_A-z_C}|=\frac{DB}{CA}$ et $ arg(\frac{z_B-z_D}{z_A-z_C})=(\overrightarrow{CA};\overrightarrow{DB})[2\pi]$.
    1. L'affixe du vecteur $\overrightarrow{AB}$ est $z_B-z_A$ , donc sa norme $AB$ est le module de ce complexe $|z_B-z_A|$ et $arg(z_B-z_A)=(\overrightarrow{u} ; \overrightarrow{AB})[2\pi]$ .
    2. $|\frac{z_B-z_D}{z_A-z_C}|=\frac{|z_B-z_D|}{|z_A-z_C|}=\frac{DB}{CA}$ et $ arg(\frac{z_B-z_D}{z_A-z_C})=arg(z_B-z_D)-arg(z_A-z_C)=(\overrightarrow{u} ; \overrightarrow{DB})-(\overrightarrow{u} ; \overrightarrow{CA})[2\pi]=(\overrightarrow{u} ; \overrightarrow{CB})+(\overrightarrow{CA} ; \overrightarrow{u})[2\pi]=(\overrightarrow{CA};\overrightarrow{CB})[2\pi]$.
    1. Les points A , B et C sont alignés si et seulement si, $ arg(\frac{z_B-z_C}{z_A-z_C})=0[\pi]$.
    2. Les droites $(AB)$ et $(CD)$ sont perpendiculaires si et seulement si $arg(\frac{z_D-z_C}{z_B-z_A})=\frac{\pi}{2}[\pi]$.
    3. Soit $\mathcal{C}$ un cercle de centre $\Omega(\omega)$ et de rayon $R$. $M\in \mathcal{C} \Leftrightarrow \Omega M=R \Leftrightarrow |z-\omega|=R$.
    4. Soit $\Delta$ la médiatrice de $[AB]$. $M(z)\in\Delta\Leftrightarrow MA=MB \Leftrightarrow |z-z_A|=|z-z_B|$.

    Forme exponentielle d'un nombre complexe.

    Définition et premières propriétés

    Pour tout réel $\theta$ , on définit le nombre exponentielle $i\theta$ par $e^{i\theta}=\cos(\theta) + i \sin(\theta)$.

    1. $e^{i0}=1$ ; $e^{i\pi}=-1$ ; $e^{i\frac{\pi}2}=i$ ; $e^{-i\frac{\pi}2}=-i$.
    2. Pour tout $\theta$ , $\theta'$ réels, $e^{i(\theta+\theta')}=e^{i\theta}\times e^{i\theta'}$.
    3. Pour tout $\theta$ , $e^{-i\theta}=\frac1{e^{i\theta}}$.
    1. $e^{i0}=cos(0)+isin(0)=1+i0=1$ etc...
    2. Simple vérification : $e^{i(\theta+\theta')}=cos(\theta+\theta')+isin(\theta+\theta')=cos(\theta)cos(\theta')-sin(\theta)sin(\theta')+i(cos(\theta)sin(\theta')+cos(\theta')sin(\theta)=(cos(\theta)+i(sin(\theta))\times (cos(\theta')+i(sin(\theta'))=(e^{i\theta}\times e^{i\theta'})$.
    3. $e^{-i\theta}=cos(-\theta)+isin(-\theta)=cos(\theta)-isin(\theta)=\overline{e^{i\theta}}=\frac{1}{e^{i\theta}}$

    Tout nombre complexe de module $r$ et d'argument $\theta$, s'écrit $z=r e^{i\theta}$.

    Cette écriture est la forme exponentielle de $z$.

    Pour tous réels $r>0$ et $r'>0$, $\theta$ et $\theta'$ , on a :

    1. $re^{i\theta}r'e^{i\theta'}=rr'e^{i(\theta+\theta')}$.
    2. $\overline{e^{i\theta}}=e^{-i\theta}=\frac1{e^{i\theta}}$.
    3. $\frac{re^{i\theta}}{r'e^{i\theta'}}=\frac{r}{r'}e^{i(\theta-\theta')}$.
    4. $(re^{i\theta})^n=r^ne^{in\theta}$

    On donne $z_1=1+i$ et $z_2=\sqrt{3}-i$.On donne $z_1=1+i$ et $z_2=\sqrt{3}-i$.

    Déterminer la forme exponentielle de $z_1$, $z_2$, $z_1^{12}$, $z_1\times z_2$, et $\frac{z_1}{z_2}$.

    Exercices

    Calculer avec la forme algébrique

    On donne les nombres complexes : $$z_1=-1+2i \textrm{ et } z_2=3+4i.$$ Déterminez la forme algébrique de : $z_1+z_2$, $z_1-z_2$; $2z_1-3z_2$; $z_1\times z_2$.

    Donnez la forme algébrique des nombres complexes suivants :

    1. $(1+i)^2$
    2. $(1-i)^2$
    3. $(3-i)^2$

    On pose $j=-\frac12+i\frac{\sqrt{3}}{2}$.

    1. Donnez la forme algébrique de $j^2$.
    2. Déterminer le discriminent du polynôme : $X^2+X+1$.
    3. Vérifiez que $1+j+j^2=0$.

    Donnez la forme algébrique des nombres complexes suivants : $$(2+i)^2(1-3i) \textrm{ et } (5-2i)(1+4i)(2-i).$$

    $x$ et $y$ sont deux nombres réels. Quelle est la forme algébrique de $(x+1+iy)(x-1-iy)$.

    Manipuler partie réelle et partie imaginaire

    On donne les nombres complexes : $$z_1=1-3i\textrm{, } z_2=4+2i \textrm{, }z_3=5-2i.$$

    Calculez :

    1. $Re(z_1+z_2+z_3)$
    2. $Im(iz_1)$
    3. $Im(z_1z_2)$
    4. $Re(2z_1-3z_2+z_3)$

    $z$ est un nombre complexe. Dans chacun des cas suivants, précisez si $Z$ est réel ou imaginaire pur ou ni l'un ni l'autre.

    1. $Z=z+\bar{z}-3i$
    2. $Z=z-\bar{z}+5i$
    3. $Z=z\bar{z}-z+\bar{z}$
    4. $Z=\bar{z}(z+i)+i(5i-z)$

    Dans chacun des cas suivants, exprimez $\bar{Z}$ en fonction de $\bar{z}$.

    1. $Z=-2+iz$
    2. $Z=(i+z)(2-iz)$
    3. $Z=(2iz+3)^2$
    4. $Z=\frac{1+iz}{2z-i}$

    Déterminer la forme algébrique

    Déterminez la forme algébrique de chacun des nombres complexes suivants :

    1. $i(1-i)$
    2. $(2-3i)(4+i)$
    3. $\frac{3+2i}{4-i}$
    4. $\frac{1}{2+3i}$
    5. $\frac{2}{1+i}-\frac{3}{1-i}$
    6. $\frac{2+3i}{5-2i}$
    7. $(1+i)(4-3i)(1-i)$
    8. $(3+i)^2(3-2i)$
    9. $\frac{2-5i}{3+2i}$
    10. $\frac{1}{i\sqrt{2}-3}$
    11. $2i-\frac3{2-i}$

    On note $z=x+iy$, $x$ et $y$ réels.On pose : $$Z=\frac{z-1}{z+1}, z\ne-1$$ Quelle est la forme algébrique de Z ?

    Résolvez chacune des équations suivantes :

    1. $(3-2i)z=i-2$
    2. $(2+i)\bar{z}=3i$

    On note $z_1=\frac{2i+1}{i+2}$ et $z_2=\frac{1-2i}{2-i}$.

    1. Pourquoi peut on affirmer sans calcul que $z_1+z_2$ est réel et $z_1-z_2$ imaginaire pur?
    2. Retrouvez ces résultats par le calcul.

    Résolution d'équation

    Résolvez dans $\mathbb{C}$ les équations suivantes et donnez les résultats sous forme algébrique.

    1. $3iz-2+4i=(1-2i)z+6$
    2. $(3+2i)z=2i\bar{z}-5i$
    3. $z^2-(2+3i)^2=0$
    4. $z^2+4=0$
    5. $iz^2+(3-4i)z=0$
    6. $\frac{z+1}{z-1}=i$
    7. $z^2-2z+4=0$
    8. $z^2-8z+25=0$
    9. $z^2+2\sqrt{3}z+3=0$
    10. $(2iz+i)(4z-8-4i)=0$
    11. $4\bar{z}+2i-4=0$
    12. $(z^2+2)(z^2-4z+4)=0$
    13. $\frac{z-3}{z-2}=z$
    14. $z^2-2(1+\sqrt{2})z+2(\sqrt{2}+2)=0$

    On donne l'équation $(E)$ : $$z^3-12z^2+48z-128=0.$$

    1. Vérifiez que 8 est solution de $(E)$.
      1. Déterminez des réels $a$, $b$ et $c$ tels que pour tout $z$ de $\mathbb{C}$, $$z^3-12z^2+48z-128=(z-8)(az^2+bz+c)$$
      2. Résolvez dans $\mathbb{C}$ l'équation $(E)$.

    Résoudre les systèmes suivant :

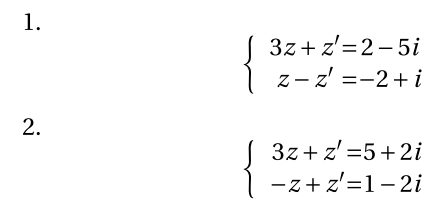
    Forme trigonométrique

    Écrivez sous forme trigonométrique chacun des complexes suivants :

    1. $\sqrt{3}-i\sqrt{3}$
    2. $2i$
    3. $\frac{1}{1+i}$
    4. $3+3i\sqrt{3}$
    5. $2-2i\sqrt{3}$
    6. $-\sqrt{2}+i\sqrt{2}$
    7. $2-2i$
    8. $-3i$
    9. $-5$
    10. $-\frac25+\frac{2i\sqrt{3}}{5}$
    11. $\frac{3}{1-i}$
    12. $(1-i\sqrt{3})(1+i)$
    13. $\frac{1+i\sqrt{3}}{2-2i}$
    14. $-2(\cos(\theta)+i\sin(\theta))$
    15. $3(\sin(\theta)+i\cos(\theta))$

    Formes exponentielles

    Écrivez sous forme exponentielle les complexes suivants :

    1. $2\sqrt{3}-2i$
    2. $(2-2i)(3+i\sqrt{3})$
    3. $-2i(\cos(\frac{\pi}{5})+i\sin(\frac{\pi}{5}))$
    4. $(2-2i)(1+i)$
    5. $2i(\sqrt{2}+i\sqrt{6})$

    Donnez le module et l'argument de chacun des nombres suivants :

    1. $\sqrt{2}e^{2i\theta}$
    2. $-e^{-i\theta}$
    3. $-2e^{i\theta}$

    On pose $z_1=-3e^{-i\frac{\pi}{3}}$ et $z_2=2-2i$.

    1. Donnez la forme algébrique de $z_1$ et de $z_1z_2$.
    2. Écrivez $z_1$, $z_2$ et $z_1z_2$ sous forme exponentielle, puis sous forme trigonométrique.
    3. Déduisez-en la valeur exacte de : $$\cos(\frac{5\pi}{12}) \textrm{ et }\sin(\frac{5\pi}{12}).$$

    On pose $z_1=e^{i\frac{\pi}3}$, $z_2=3e^{-i\frac{\pi}4}$ et $z_3=\sqrt{2}e^{i\frac{2\pi}3}$.

    Donnez une forme exponentielle des complexes suivants :

    1. $z_1z_2$
    2. $\frac{z_1}{z_2}$
    3. $z_1^3$
    4. $z_1z_2z_3$
    5. $z_3^4$
    6. $\frac{z_2}{z_3}$

    Donnez une forme exponentielle de chacun des complexes suivants :

    1. $z_1=-2e^{i\frac{\pi}{3}}$
    2. $z_2=(1-i)e^{-\frac{\pi}{6}}$
    3. $z_3=-\sqrt{2}e^{\frac{\pi}{5}}$
    4. $z_4=\frac{3}{e^{i\frac{\pi}{7}}}$

    Géométrie

    1. Placez les points A, B,C, D d'affixes respectives $-4-3i$, $3-2i$, $4+5i$, $-3+4i$.
    2. Quelle est la nature du quadrilatère ABCD?
    1. Placez les points A, B,C d'affixes respectives $-3-2i$, $2-i$, $-2+6i$.
    2. Quelle est la nature du triangle ABC?

    Les points A et B ont pour affixes respectives $a=2$ et $b=2e^{i\frac{3\pi}{4}}$.

    I est le milieu de $[AB]$.

    1. Faites une figure
      1. Trouvez une mesure de l'angle $(\overrightarrow{u};\overrightarrow{OI})$
      2. Déterminez la forme algébrique de l'affixe de I.
      3. Déduisez-en que $OI=\sqrt{2-\sqrt{2}}$.
      1. Donnez l'affixe de I sous forme exponentielle.
      2. Déduisez-en la valeur exacte de $$\cos(\frac{\pi}8) \textrm{ et } \sin(\frac{\pi}8).$$
    1. Calculez $(1+i)^2$, $(1+i)^4$ et $(1+i)^8$
    2. $M_n$ est le point d'affixe $(1+i)^n$, $n\in\N$. Pour quelles valeurs de $n$, le point $M_n$ appartient-il à l'axe des abscisses?

    Dans chacun des cas suivants, représentez l'ensemble des points M dont l'affixe $z$ vérifie l'égalité donnée.

    1. $arg(z)=\frac{\pi}3 [2\pi]$
    2. $arg(z)=-\frac{\pi}6 [2\pi]$
    3. $arg(iz)=5\frac{\pi}4 [\pi]$
    4. $arg(\frac{z}{1+i})=\frac{\pi}4 [\pi]$
    1. Placez les points A,B,C et D d'affixes respectives : $$z_A=1,5i \textrm{; } z_B=3,5+i \textrm{; } z_C=1-1,5i \textrm{ et } z_D=-2,5-i.$$
    2. Quelle est la nature du quadrilatère ABCD? Justifiez.

    On donne dans le plan complexe les points A, D et C d'affixes respectives : $$z_A=-2 \textrm{, } z_B=1+i \textrm{ et } z_C=-1-3i.$$

    1. Placez les points A,B et C.
    2. Quelle est la nature du triangle ABC? Justifiez.

    Sur la figure ci-dessous, on a placé les points A,B, C d'affixes respectives $-i$, $2+i$, $-1+3i$, et les droites médiatrices $\Delta$ et $\Delta '$ des segments $[AB]$ et $[BC]$ respectivement.

    1. Prouvez que : $$M(z)\in\Delta \Leftrightarrow |z-(-i)|=|z-2-i|.$$
    2. Caractérisez de manière analogue l'appartenance d'un point $M(z)$ à la médiatrice $\Delta '$.
    3. Déterminez et représentez l'ensemble des points $M(z)$ tels que : $$|z+i|=|z-2-i|=|z+1-3i|.$$

    Dans chaque cas, déterminer l'ensemble des points $M$ d'affixe $z$ tels que :

    1. $|z-3|=2$
    2. $|z+2i|=1$
    3. $|z-i|=|z+2|$
    4. $|z-(2+i)|=|z|$
    1. Déterminez l'ensemble des points M du plan complexe dont l'affixe $z$ vérifie, $$|\bar{z}+i|=|z+2|.$$
    2. Déterminez l'ensemble des points M du plan complexe dont l'affixe $z$ vérifie $|\bar{z}+i|=2$
    3. Même question avec $|\bar{z}-2i|=|z+2|$.

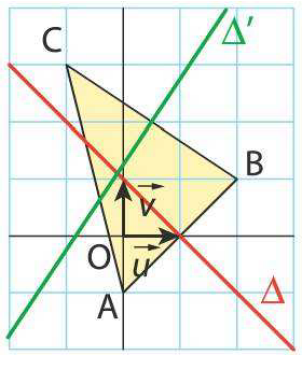
    Sur la figure ci-dessous, on a représenté les cercles de centres B et C d'affixes respectives $z_B=2+i$ et $z_C=-2+2i$, et passant par l'origine O du repère. On note $\Gamma_{B}$ et $\Gamma_C$ les disques fermés correspondants.

    1. Prouvez que $$M(z)\in\Gamma_B \textrm{ si, et seulement si } |z-2-i|\leq \sqrt{5}.$$
    2. Caractérisez de manière analogue l'appartenance du point $M(z)$ au disque $\Gamma_C$.
    3. Caractérisez l'ensemble $\mathcal{E}$ des points $M(z)$ tels que : $$|z-2-i|\leq \sqrt{5} \textrm{ et } |z+2-2i|\leq 2\sqrt{2}.$$

    Synthèse

    ROC: Restitution Organisée de Connaissances

    Pré-requis:

    Le plan complexe est muni d'un repère orthonormé direct $(O;\overrightarrow{u},\overrightarrow{v})$. Si $z$ et $z'$ sont deux nombres complexes non nuls, alors $arg(zz')=arg(z)+arg(z')[2\pi]$.

    1. Démonstration : $z$ et $z'$ sont deux nombres complexes non nuls.Démontrez que :
      1. $arg(\frac{z}{z'})=arg(z)-arg(z')[2\pi]$
      2. $arg(\frac1{z^2})=-2arg(z) [2\pi]$
    2. Application : $z$ est un nombre complexe non nul d'image M. On associe à M le point $M'$ d'affixe $\frac1{z^2}$. On note $d$ la demi-droite d'origine O et de vecteur directeur $\overrightarrow{w}$ tel que $(\overrightarrow{u},\overrightarrow{w})=\frac{\pi}3$.
      1. Quel est l'ensemble des points $M'$ lorsque $M$ décrit la demi-droite $d$ privée de O?
      2. Quel est l'ensemble des points $M$ lorsque $M'$ décrit la demi-droite $d$ privée de O?

    Bac

    $z$ est un complexe non nul $z'=\frac{-2}{z}$.

    1. Quelle relation lie les modules de $z$ et $z'$? Les arguments de $z$ et $z'$?
    2. Dans le plan complexe muni d'un repère orthonormé direct$(O;\overrightarrow{u},\overrightarrow{v})$, $M$ est le point d'affice $z$, $M'$ le points d'affixe $z'$. $\mathcal{D}$ est le disque de centre O et de rayon 2, privé de O. A est le point d'affixe $a$ telle que $|a|=2$ et $arg(a)=\frac{\pi}{4}[2\pi]$.
      1. Quel est l'ensemble des points $M'$ lorsque le point M décrit $\mathcal{D}$?
      2. Quel est l'ensemble des points $M'$ lorsque le point M décrit le segment $[OA]$ privé de O?

    Le plan est rapporté à un repère orthonormé direct $(O;\overrightarrow{u},\overrightarrow{v})$. On a tracé dans ce repère la courbe $\mathcal{C}$ représentative de la fonction $f:x\longmapsto \frac{x}{x-1}$ et la droite $d$ d'équation $x=1$. Au point $M$ d'affixe $z$, on associe l point $M'$ d'affixe $Z=z^2-2(1+i)z.$

    Démontrez que si $M$ est un point de $\mathcal{C}$, alors $M'$ est un point de l'axe des abscisses.

    ROC

    pré requis: $z$ est un nombre complexe tel que $z=a+ib$ où $a$ et $b$ sont deux réels. On note $\bar{z}$ le conjugué de $z$ tel que $\bar{z}=a-ib$.

    1. Démonstration
      1. Démontrez que pour tous nombres complexes $z$ et $\bar{z}$, $$\overline{z\times z'}=\overline{z}\times\overline{z'}.$$
      2. Démontrez par récurrence que pour tout entier naturel $n$ non nul et tout nombre complexe $z$ : $$\overline{z^n}=(\bar{z})^n$$
    2. Application 1 : On considère l'équation $(E): z^4=-4$, où $z$ est un nombre complexe.
      1. Démontrez que si $z$ est solution de $(E)$, alors $-z$ et $\bar{z}$ sont aussi solutions de $(E)$.
      2. On considère le nombre complexe $z_0=1+i$.
        • Écrivez $z_0$ sous forme exponentielle.
        • Vérifiez que $z_0$ est solution de $(E)$.
      3. Déduisez des questions précédentes trois autres solutions de l'équation de l'équation $(E)$.
    3. Application 2 : Le plan complexe est rapporté à un repère orthonormé direct $(O;\overrightarrow{u},\overrightarrow{v})$. A, B, C, D ont pour affixes respectives : $$z_A=1+i \textrm{, } z_B=-1+i \textrm{, } z_C=-1-i \textrm{, } z_D=1-i$$
      1. Placez A, B, C, D dans le repère.
      2. Soit E le point d'affixe $-1+\sqrt{3}$. Démontrez que le triangle BCE est équilatéral et que $(\overrightarrow{CE};\overrightarrow{CB})=\frac{\pi}{3}[2\pi]$.
      3. F est le point d'affixe $-i(1+\sqrt{3})$. Démontrez que $\frac{z_A-z_E}{z_A-z_F}$ est un réel. Déduisez-en que les points A, E et F sont alignés.

    Bac

    Le plan complexe est muni d'un repère orthonormé direct $(O;\overrightarrow{u},\overrightarrow{v})$, d'unité graphique 2 cm.

    On réalisera une figure que l'on complétera tout au long de l'exercice.

    On considère les points A d'affixe $i$, B d'affixe $-2i$ et D d'affixe 1.

    On appelle E le point tel que le triangle ADE est équilatéral direct.

    Soit $f$ l'application qui à tout point M d'affixe $z$ ( $z\ne i$) associe le point $M'$ d'affixe $z'$ définie par :$z'=\frac{2z-i}{iz+1}$.

    1. Démontrez que le point E a pour affixe : $$(\frac12+\frac{\sqrt{3}}{2})(1+i).$$
      1. Exprimez sous forme algébrique l'affixe du point $D'$ associé au point D par l'application $f$.
      2. Démontrez que pour tout nombre complexe $z$ différent de $i$, $(z'+2i)(z-i)=1$.
      3. Déduisez-en que pour tout point $M$ d'affixe $z$ $(z\ne i)$ :$$BM'\times AM=1 \textrm{ et }$$ $$ (\overrightarrow{u};\overrightarrow{BM'})=-(\overrightarrow{u};\overrightarrow{AM})+k\times 2\pi, \textrm{ où } k\in\Z.$$
      1. Démontrez que les points D et E appartiennent au cercle $\mathcal{C}$ de centre A et de rayon $\sqrt{2}$.
      2. En utilisant les résultats de la question 2) b), placez le point $E'$ associé au point E par l'application $f$.Vous laisserez apparents les traits construction.
    4. Quelle est la nature du triangle $BD'E'$? Justifiez.

    BAC

    Dans le plan complexe muni d'un repère orthonormé direct, on associe à tout point M d'affixe $z$ non nulle, le point $M'$ milieu du segment $[MM_1]$ où $M_1$ est le point d'affixe $\frac1{z}$.

    Le point $M'$ est appelé image de M.\begin{enumerate}

      1. Démontrez que : $$OM\times OM_1=1 \textrm{ et } (\overrightarrow{u};\overrightarrow{OM_1})=-(\overrightarrow{u};\overrightarrow{OM})[2\pi].$$
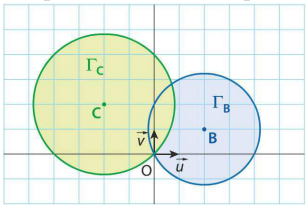
      2. Sur la figure ci-dessous, le point A appartient au cercle de centre O et de rayon 2. Construisez le point $A'$ image de A (On laissera apparent les traits de construction.)
      1. Justifiez que pour tout nombre complexe $z$ non nul, le point $M'$ a pour affixe : $$z'=\frac12(z+\frac1{z}).$$
      2. B et C sont les points d'affixes respectives $2i$ et $-2i$. Calculez les affixes des points $B'$ et $C'$, images respectives de B et C.
      3. Placez B,C, $B'$, $C'$ sur la figure précédente.
    3. Déterminez l'ensemble des points M tel que $M'=M$.
    4. Prise d'initiative : Démontrez que si M appartient au cercle de centre O et de rayon 1, alors son image $M'$ appartient au segment $[KL]$ où K et L sont les points d'affixes respectives $-1$ et $1$.

    Le plan complexe est muni d'un repère orthonormé direct $(O;\overrightarrow{u},\overrightarrow{v})$, d'unité graphique 2 cm.

    On considère les points A,B et C d'affixes respectives : $$z_A=-\frac32+i\frac{\sqrt{3}}{2}\textrm{, }z_B=\overline{z_A}\textrm{ et } z_C=-3.$$

    Partie A

    1. Écrivez $z_A$ et $z_B$ sous forme exponentielle.
    2. Placez les points A, B ,C.
    3. Démontrez que le triangle ABC est équilatéral.

    Partie B

    Soit $f$ l'application qui a tout point M d'affixe $z$ associe le point $M'$ d'affixe : $$z'=\frac13iz^2.$$ On note $O'$, $A'$, $B'$ les points associés par $f$ aux points O, A, B,C respectivement.

      1. Déterminez la forme exponentielle des affixes des points $A'$, $B'$ et $C'$.
      2. Placez les points $A'$, $B'$ et $C'$.
      3. Démontrez l'alignement des points O,A,$B'$ ainsi que celui des points O,B,A'.
    2. Démontrez que si M appartient à la droite $(AB)$, alors $M'$ appartient à la parabole d'équation $y=-\frac13 x^2+\frac34$.

    BAC

    Le plan complexe est muni d'un repère orthonormé direct $(O;\overrightarrow{u},\overrightarrow{v})$.On considère l'application $f$ du plan dans lui-même qui, à tout point M d'affixe $z$, associe le point $M'$ d'affixe $z'=z^2-4z$.

    1. On note A et B les points d'affixes respectives $z_A=1-i$ et $z_B=3+i$.
      1. Calculez les affixes des points $A'$ et $B'$, images respectives des points A et B par $f$.
      2. Soit $M_1$ et $M_2$ deux point d'affices respectifs $z_1$ et $z_2$ qui ont la même image par $f$. Démontrez $M_1=M_2$ ou que $overrightarrow{M_1C}=\overrightarrow{CM_2}$ où $C$ est d'affixe $2$.
    2. I est le point d'affixe $-3$.
      1. Démontrez que le quadrilatère $OMIM'$ est un parallélogramme si, et seulement si, $z^2-3z+3=0$.
      2. Résoudre dans $\mathbb{C}$ l'équation $z^2-3z+3=0$.
      1. Exprimez $z'+4$ en fonction de $z-2$. Déduisez-en une relation entre $|z'+4|$ et $|z-2|$, puis entre $arg(z'+4)$ et $arg(z-2)$.
      2. Les points J et K ont pour affixes respectives $z_J=2$ et $z_k=-4$.
        Démontrez que pour tous les points M du cercle $\mathcal{C}$ de centre J et de rayon 2 ont leur images $M'$ sur un même cercle que l'on déterminera.
      3. E est le point d'affixe $z_E=-4-3i$. Donnez la forme exponentielle de $z_E+4$ et, à l'aide de 3. a), démontrez qu'il existe deux points dont l'image par $f$ est E.

    Soient $a$ et $b$ deux réels. On appelle suite récurrente d'ordre 2 une suite définie par $u_0$, $u_1$ et pour tout $n$, $$u_{n+2}=au_{n+1}+bu_n(1).$$

    1. $u_2=2\times 2+-2\times 1=2$
      $u_2-u_1=0$, $u_1-u_0=1$ donc $u$ n'est pas arithmétique.
      $\frac{u_2}{u_1}=1$ , $\frac{u_1}{u_0}=2$ donc $u$ n'est pas géométrique.
    2. On pose $a=2$ et $b=-2$. On cherche $r$ tel que $u_n=r^n$ vérifie $(1)$.
      1. Montrer que si $r$ est non nul, il est solution de l'équation $r^2-2r+2=0 (2)$.
      2. Résoudre (2).
      3. On note $r_1$ et $r_2$ les solutions de $(2)$. Montrer que si $u_n=cr_1^n+dr_2^n$; alors $u_n$ vérifie $(1)$. On admet que toute suite vérifiant $(1)$ s'écrit ainsi.
      4. Déterminer $c$ et $d$ sachant que $u_0=1$ et $u_1=2$.
      5. Exprimer alors $u_n$ en fonction de $n$.
    Licence Creative Commons
    Maths et Informatique à Saint Dizier Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.