1. Soit $f:x\mapsto x^2$. Montrer que $f$ est dérivable sur $\mathbb{R}$.
2. Soit $g:x\longmapsto \sqrt{x}$. Montrer que $g$ n'est pas dérivable en 0.

Soit $f:x\mapsto \sqrt{x^2+2x}$ définie sur $[0;+\infty[$. Déterminons l'ensemble de dérivabilité de $f$ ainsi que sa dérivée.

Simplifier au maximum : $\frac{e^{3x}e^{2x-1}}{e^{-5x}e^x}$

1. Résoudre dans $\mathbb{R}$ les équations et les inéquations suivantes : a)$e^{-x}+1=0$ b)$e^{3x+1}-e^{-x}<0$ c)$e^{2x}+2e^x<3$
2. Déterminer les variations de la fonction définie sur $\mathbb{R}$ par $f(x)=xe^{-x+1}$

Pour chacune des fonctions suivantes déterminer les limites de la fonction $f$ aux bornes de son ensemble de définition .

1. $f:x\longmapsto e^{3-x}$ sur $\mathbb{R}$
2. $f:x\longmapsto \frac{e^{2x}+2}{e^x-1}$ sur $\mathbb{R}^*$

Déterminer les limites suivantes :

1. \lim\limits_{x\to +\infty} x^3-e^{2x+1}$
2. $\lim\limits_{x\to +\infty} \frac{e^x-x}{2e^x+3}$

Exprimez la fonction dérivée $f$' de la fonction $f$ en précisant sur quel(s) intervalle(s) $f$ est dérivable.

1. $f(x)=x^3-3x^2+x-1$
2. $f(x)=x^{100}+2x^{51}-5$
3. $f(x)=(4-3)^3$
4. $f(x)=(7x^2+x-3)^5$
5. $f(x)=x^2+\frac1{1+x^2}$
6. $f(x)=\frac{1}{\sqrt{2x}}$
7. $f(x)=x\sqrt{x}$
8. $f(x)=\sqrt{x^3-2x}$
9. $f(x)=\sqrt{\frac{3x-2}{2x-3}}$
10. $f(x)=\frac1{x}$
11. $f(x)=\frac{1}{(-2x-3)^3}$
12. $f(x)=x\sqrt{4-x}$

On a tracé les courbes représentatives des fonctions $f$ et $g$ définies sur $\mathbb{R}$ par : $f(x)=\sqrt{x^2-x+1}$ et $g(x)=-\frac14 x^2+x+\frac14$

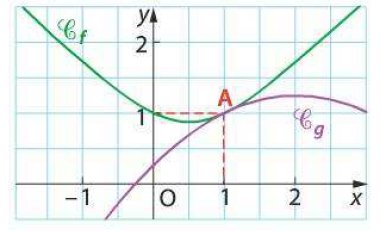
1. Que dire de ces deux courbes au point d'abscisse 1?
2. Démontrer les conjectures.

$f$ est fonction définie sur $\mathbb{R}$ par $f(x)=x+\sqrt{1+x^2}$.

1. Vérifier que pour tout $x$ réel, $\sqrt{1+x^2}\times f'(x)=f(x)$
2. Déduisez en que pour tout réel $x$ : $(1+x)^2f''(x)+xf'(x)-f(x)=0$

On a tracé ci-dessous la courbe $\mathcal{C}$ représentative de la fonction $f$ définie sur $[-1;+\infty[$ par $f(x)=\sqrt{x+1}$ ainsi que la droite $d$ d'équation $y=\frac{x}2+1.$

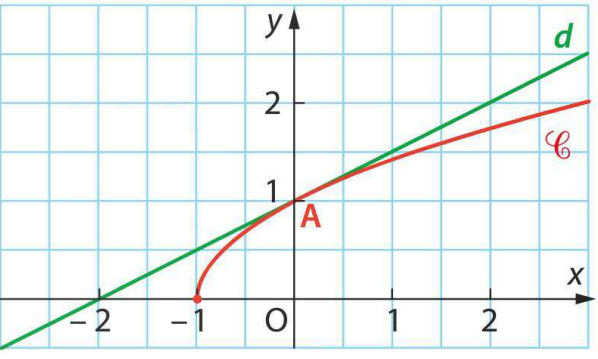
1. Démontrer que la droite $d$ est tangente à $\mathcal{C}$ au point A d'abscisse 0.
2. On se propose de démontrer que pour tout $x$ de l'intervalle $[-1;+\infty[$, la courbe $\mathcal{C}$ est en dessous de $d$.
   Pour cela, on considère la fonction $g$ définie sur $[-1;+\infty[$ par $g(x)=\sqrt{x+1}-\frac{x}2-1$.
   Etudier le variations de la fonction $g$ et dressez son tableau de variations. Conclure.

1. $g$ est la fonction définie sur $\mathbb{R}$ par : $$g(x)=x^3-3x-3.$$
   1. Démontrez que l'équation $g(x)=0$ a une solution unique $\alpha$ dans $\mathbb{R}$.
   2. Donnez une valeur approchée de $\alpha$ à $10^{-1}$ près.
   3. Déduisez des questions précédentes le signe de $g(x)$.
2. $f$ est la fonction définie sur $\mathbb{R}\backslash\{-1;1\}$ par : $$f(x)=\frac{2x^3+3}{x^2-1}.$$
   1. Démontrez que pour tout $x$ de $\mathbb{R}\backslash\{-1;1\}$ : $$f'(x)=\frac{2xg(x)}{(x^2-1)^2}.$$
   2. Dressez le tableau de variation de $f$.
   3. Démontrez que le point A de $\mathcal{C}$ d'abscisse $\alpha$ a pour ordonnée $$f(\alpha)=\frac{3(2\alpha+3)}{\alpha^2-1}.$$

1. Montrer que la fonciton $f:x\longmapsto x^3-4x+1$ s'annule une seule fois sur $[\frac{2\sqrt{3}}{3};2]$.

2. On considère l'algorithme suivant dans lequel $f$ est une fonction numérique.

   
       def f(x):
           return x^3-4x+1
       def mystere(a,b,p):
           while b-a>p:
               if f((a+b)/2)*f(b)<0:
                   a=(a+b)/2
               else:
                   b=(a+b)/2
           return b
       print(mystere(1,2,0.01))
           

Que renvoie la fonction mystère?

$a$ est un nombre tel que $-1<a<0$. La suite $u$ est définie par $u_0=a$ et pour tout $n$ de $\mathbb{N}$, $u_{n+1}=u_n^2+u_n$.

1. Étudiez le sens de variation de la suite $u$.
2. $f$ est la fonction définie sur $\mathbb{R}$ par $f(x)=x^2+x$.
1. Démontrez que si $x\in]-1;0[$, alors il en est de même pour $f(x)$.
2. Démontrez par récurrence que pour tout $n$ de $\mathbb{N}$ : $$-1<u_n<0.$$
3. Étudiez la convergence de la suite $u$ et déterminez sa limite si elle existe.

$f$ est la fonction définie sur $\mathbb{R}$ par : $$f(x)=(e^x+e^{-x})^2-(e^x-e^{-x})^2.$$

1. Représentez $f$ sur votre calculatrice.
2. Que conjecturez vous? Prouvez le.

On considère les fonctions $f$ et $g$ définies sur $\mathbb{R}$ par $f(x)=\frac12(e^{2x}+1)$ et $g(x)=e^x$, ainsi que la droite $\Delta$ tangente à $\mathcal{C}_g$.

1. Montrer que $\Delta$ est tangente à $\mathcal{C}_f$
2. On se propose d'étudier la position relative des courbes $\mathcal{C}_f$, $\mathcal{C}_g$ et $\Delta$.
1. Justifiez que $\mathcal{C}_g$ est au dessus de $\Delta$.
2. On définit la fonction $d$ sur $\mathbb{R}$ par $$d(x)=g(x)-f(x).$$ Étudiez les variations de $d$, puis déduisez-en la position relative de $\mathcal{C}_f$ et $\mathcal{C}_g$.
3. Quel encadrement de $e^x$, $x\in\mathbb{R}$, pouvez-vous en déduire?

Résolvez dans $\mathbb{R}$ les équations et les inéquations suivantes :

1. $e^{2x^2+3}=e^{7x}$
2. $e^{x+1}=e^{\frac2{x}}$
3. $3e^{2x}+e^x-4=0$
4. $e^{x^2}=(e^{-x})^2e^3$
5. $e^{x}\leq e^{x^2-12}$
6. $e^{2x+1}\leq e^{\frac3{x}}$
7. $e^{2x}-3e^x-1\geq 0$
8. $e^{x}+e^{-x}-2\geq 0.$

Calculez la dérivée de la fonction $f$ proposé sur l'intervalle I indiqué.

1. $f(x)=e^x-x-4$; $I=\mathbb{R}$
2. $f(x)=(x^2+x-1)e^{-x}$; $I=\mathbb{R}$
3. $f(x)=\frac{e^x}{e^x-1}$; $I=]0;+\infty[$
4. $f(x)=\frac{1-e^{-x}}{x}$; $I=]0;+\infty[$
5. $f(x)=x+2-\frac{2e^x}{e^x+1}$; $I=\mathbb{R}$

Déterminer la limite de la fonction $f$ en $+\infty$ et en $-\infty$.

1. $f(x)=e^x+e^{-x}$
2. $f(x)=e^{-x^2-1}$
3. $f(x)=e^{2x}-e^{-x}$
4. $f(x)=e^{3x}-e^{2x}+2.$
5. $f(x)=\frac{e^x-1}{2e^x+1}$
6. $f(x)=\frac{e^{2x}+e^x+1}{e^x+2}$

Déterminer la limite de la fonction $f$ en $0$ et en $+\infty$.

1. $f(x)=e^{\frac1{x}}$
2. $f(x)=\frac1{x}e^{\frac1{x}}$
3. $f(x)=e^{2x}-e^{-x}$
4. $f(x)=\frac{e^{2x}}{x^2}$
5. $f(x)=x^2e^{-2x}$

Déterminer la limite de la fonction $f$ en $0$.

1. $f(x)=\frac{e^x-1}{2x}$
2. $f(x)=\frac{1-e^{-x}}{x}$
3. $f(x)=\frac{e^{2x}-1}{x}$
4. $f(x)=\frac{e^{3x}-1}{5x}$

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=(1-x)e^x$. On appelle A et B les points de la courbe représentative de $f$ , $\mathcal{C}$, d'abscisses respectives 1 et -1.

1. Démontrez que les tangentes en A et en B à la courbe $\mathcal{C}$ sont perpendiculaires.
2. Dans cette question, on se propose d'étudier la position de la courbe $\mathcal{C}$ par rapport à la tangente T en B à $\mathcal{C}$. Pour cela, on considère la fonction $g$ définie sur $\mathbb{R}$ par : $$g(x)=(1-x)e^x-\frac{1}{e}(x+3).$$
1. Calculer $g'(x)$ et $g''(x)$ pour tout nombre $x$.
2. Étudiez le sens de variation de $g'$ et précisez $g'(-1)$.
3. Déduisez en le sens de variation de $g$.

On considère la fonction $f$ définie sur $\mathbb{R}$, de courbe représentative $\mathcal{C}$, par : $$f(x)=ax+b+xe^x \textrm{ où a et b sont deux nombres. }$$

1. Trouvez $a$ et $b$ sachant que la tangente à $\mathcal{C}$ en $A(0;2)$ coupe l'axe des abscisses au pint d'abscisse 2.
2. 1. Calculez $f'(x)$ puis $f''(x)$.
   2. Déduisez-en le tableau de variation de $f'$.

A. Lecture graphique

Dans un repère orthonormé, on a tracé les courbes $\mathcal{C}$ et $\mathcal{F}$ représentatives de deux fonctions définies et dérivables sur $\mathbb{R}$.

On note ces fonctions $g$ et $g'$.

On sait que l'une des fonctions est la dérivée de l'autre.

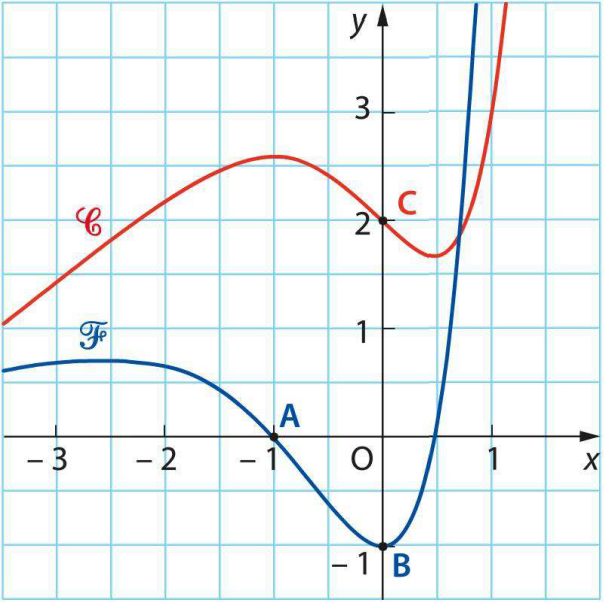
1. Associez à chaque fonction sa courbe. On justifiera les résultats à l'aide d'un tableau de variation partiel qui sera complété dans la suite du problème.
2. Quel est le coefficient directeur de la tangente à $\mathcal{C}$ au point d'abscisse

B. Détermination de la fonction $g$

La fonction $g$ est définie sur $\mathbb{R}$ par $g(x)=(ax^2+bx+c)e^x$, où a,b,c sont trois nombres.

1. A l'aide des points A,B,C clairement définis sur la figure, trouvez a,b,c.
2. Complétez alors le tableau de variation de $g$ en justifiant vos réponses.
3. On note T la tangente en C à la courbe $\mathcal{C}$ et $\phi$ la fonction définie sur $\mathbb{R}$ par $\phi(x)=g(x)-(2-x).$
   1. Etudiez les variations de $\phi$.
   2. Déduisez-en la position de $\mathcal{C}$ par rapport à T.

1. $f$ est une fonction définie et dérivable sur un intervalle I. M est un point dela courbe $\mathcal{C}$ représentative de $f$, d'abscisse $a$ telle que $a$ appartient I. Démontrez que la tangente en M à $\mathcal{C}$ passe par l'origine du repère si et seulement si $f(a)-af'(a)=0.$
2. Application
   $f$ est la fonction définie sur $]-2;+\infty[$ par $f(x)=\frac{e^{x}}{x+2}$.
   On note $\mathcal{C}_f$ sa courbe représentative.
   Démontrez qu'il existe deux tangentes à $\mathcal{C}_f$ passant par l'origine du repère.

ROC

pré requis : La fonction exponentielle $f$ définie sur $\mathbb{R}$ par $f(x)=e^{x}$ est dérivable sur $\mathbb{R}$ et pour tout $x$, $$f'(x)=f(x).$$

1. Démonstration
   1. Étudiez les variations de la fonctions $g$ définie sur $\mathbb{R}$ par $g(x)=e^x-x$. Déduisez-en $\lim\limits_{x\to +\infty} e^x$ et $\lim\limits_{x\to -\infty} e^x$
2. Application:
   $f$ est la fonction définie sur $\mathbb{R}$ par $f(x)=x^2e^{-x}$.
   Établir le tableau de variation de $f$.

BAC

A. $f$ est la fonction définie sur $[0;+\infty[$ par : $$f(x)=\frac{x-1}{x+1}-e^{-x}$$ On note $\mathcal{C}$ sa courbe représentative dans un repère.

1. Démontrer que $\mathcal{C}$ admet une asymptote horizontale dont on donnera une équation.
2. Étudiez les variations de $f$ sur $[0;+\infty[$.
3. Déterminez une équation de la tangente T à $\mathcal{C}$ au point d'abscisse 0.
4. Démontrez que l'équation $f(x)=0$ admet une solution unique dans l'intervalle $[1;2]$. On note $u$ cette solution.
   Déterminez un encadrement d'amplitude $10^{-1}$ de $u$.

$n$ désigne un entier naturel non nul.
$f_n$ est la fonction définie sur $[0;+\infty[$ par : $$f_n(x)=\frac{x-n}{x+n}-e^{-x}.$$

Dressez le tableau de variation de $f_n$.
1. Calculez $f_n(n)$. Quel est son signe?
2. Démontrez par récurrence que pour tout $n$ de $\mathbb{N}$, $$e^{n+1}>2n+1.$$
3. Démontrez que l'équation $f_n(x)=0$ admet une solution unique dans l'intervalle $[n;n+1]$. On note $u_n$ cette solution.
1. \item Calculez $\lim\limits_{n\to +\infty} u_n$ et $\lim\limits_{x\to +\infty }\frac{u_n}{n}$.