Donner l'équation paramétrique du plan $(ABC)$ où $A(1;1;0)$ , $B(0;-1;-2)$ et $C(2;3;-1)$.

ABCDEFGH est cube. I,J,K sont les milieux respectifs de $[AB]$, $[AE]$ et $[CG]$.

Le point L est tel que : $$3\overrightarrow{EL}=2\overrightarrow{EI}$$

1. 1. Démontrez que : $$3\overrightarrow{JL}=\overrightarrow{EJ}+\overrightarrow{AB}.$$
   2. Déduisez-en que B, J, L sont alignés.
2. 1. Démontrez que les vecteurs $\overrightarrow{JL}$ et $\overrightarrow{HK}$ sont colinéaires.
   2. Déduisez-en la valeur de $k$ telle que $\overrightarrow{HK}=k\overrightarrow{JL}$

ABCD est un tétraèdre. E est le point de l'espace tel que $$\overrightarrow{AE}=\frac13\overrightarrow{BD}.$$ Les vecteurs $\overrightarrow{BA}$, $\overrightarrow{BD}$, $\overrightarrow{BE}$ sont-ils coplanaires?

ABCDEFGH est un cube. I et J sont les milieux des segments respectifs $[EB]$ et $[FG]$.

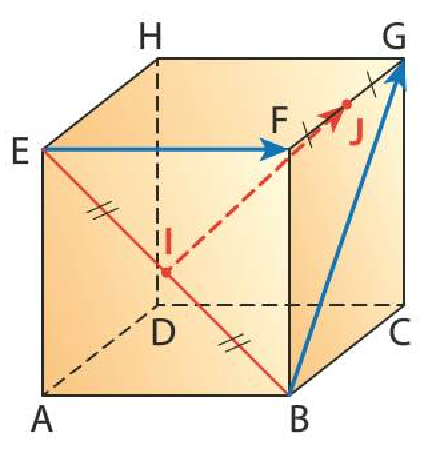
1. En décomposant le vecteur $\overrightarrow{IJ}$ de deux manières, démontrez que $2\overrightarrow{IJ}=\overrightarrow{EF}+\overrightarrow{BG}.$
2. Déduisez-en que les vecteurs $\overrightarrow{IJ}$, $\overrightarrow{EF}$ et $\overrightarrow{BG}$ sont coplanaires.

ABCD est un tétraèdre, I est le milieu de $[AB]$, J celui de $[CD]$ et O celui de $[IJ]$.

1. Complétez : $\overrightarrow{AI}+\overrightarrow{...}+\overrightarrow{JC}=\overrightarrow{AC}$.
2. Démontrez que $\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{IJ}$.
3. Justifiez que $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$.
4. Justifiez que : $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OI}$ et $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OJ}$.
5. Déduisez-en que $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{0}$

Dans chacun des cas suivants, précisez si $\vec{u}$ et $\vec{v}$ sont colinéaires.

1. $\vec{u}(2;1;-3)$ et $\vec{v}(1;2;2)$.
2. $\vec{u}(14;-24,5;17,5)$ et $\vec{v}(-4;7;-5)$.

On donne les points $A(1;-1;2)$, $B(0;5;3)$ et $C(4;-19;-1)$. Ces sont-ils alignés?

On donne les points $A(3;2;2)$, $B(-1;-4;4)$, $C(1;0;1)$ et $D(3;3;2)$. Les droites $(AB)$ et $(CD)$ sont-elles parallèles?

Déterminez les nombres $a$ et $b$ pour lesquels les vecteurs $\vec{u}(-2;a;-5)$ et $\vec{v}(-4;-6;b)$ sont colinéaires.

On donne les points $A(5;2;1)$, $B(7;3;1)$, $C(-1;4;5)$ et $D(-3;3;5)$.\\ Le quadrilatère ABCD est-il un parallélogramme?

ABCD est un tétraèdre. I est le milieu de $[BC]$. L point G est tel que $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$.

1. Démontrez que $\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GI}$
2. Déduisez-en que les points G, A, I sont alignés et que G est le centre de gravité de ABC.
3. On considère le point K tel que $$\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}+\overrightarrow{KD}=\vec{0}$$
   1. Démontrez que $3\overrightarrow{KG}+\overrightarrow{KD}=\vec{0}$.
   2. Déduisez-en que $K$, $G$, $D$ sont alignés.
   3. trouvez le réel $k$ tel que $$\overrightarrow{DK}=k\overrightarrow{DG}.$$

On donne les vecteurs $\vec{u}(-1;3;2)$ et $\vec{v}(4;0;2)$ et $\vec{w}(-7;9;4)$.

1. Calculez $3\vec{u}-\vec{v}-\vec{w}$.
2. Les vecteurs $\vec{u}$,$\vec{v}$ et $\vec{w}$ sont-ils coplanaires?

On donne les points $A(2;1;3)$, $B(-1;0;5)$, $C(1;1;1)$, $D(1;0;1)$ et $E(4;-2;1)$

1. Démontrez que les points A,B,C ne sont pas alignés.
2. La droite $(DE)$ est-elle parallèle au plan $(ABC)$?

On donne les vecteurs $\vec{u}(0;-1;1)$,$\vec{v}(-2;-1;3)$ et $\vec{w}(-1;-1;-1)$. Le triplet $(\vec{u}, \vec{v}, \vec{w})$ est-il une base des vecteurs de l'espace?

On donne les vecteurs $\vec{u}(1;1;1)$, $\vec{v}(2;7;-3)$ et $\vec{w}(1;m;2)$. Comment faut-il choisir m pour que $(O;\vec{u},\vec{v},\vec{w})$ soi un repère de l'espace?

ABCDEFGH est un cube. I et J sont les mieux des arêtes $[EH]$ et $[AB]$.
On choisit le repère $(D;\overrightarrow{DA}$, $\overrightarrow{DC}$,$\overrightarrow{DH}$.

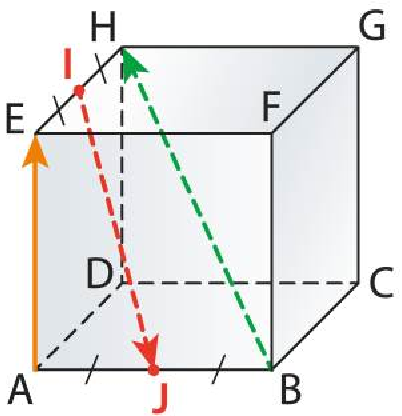
Démontrez ques les vecteurs $\overrightarrow{AE}$, $\overrightarrow{IJ}$ et $\overrightarrow{BH}$ sont coplanaires.

ABCDEF est un prisme droit. I, J, K, L sont les mileux respectifs des arêtes $[BC]$, $[AD]$, $[BE]$ et $[CE]$.

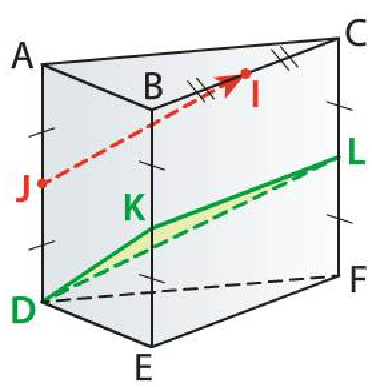
On choisit le repère $(B,\overrightarrow{BA}, \overrightarrow{BC}, \overrightarrow{BE})$.

1. Démontrez que les vecteurs $\overrightarrow{JI}$; $\overrightarrow{KL}$, et $\overrightarrow{KD}$ sont coplanaires.
2. Que pouvez-vous dire de la position relative de la droite $(IJ)$ et du plan $(DKL)$?

Dans un repère $(O;\vec{i},\vec{j}, \vec{k})$, on donnes les vecteurs $\vec{u}(0;-1;1)$, $\vec{v}(-2;-1;3)$ et $\vec{w}(-1;-1;-1)$.

On pose $\overrightarrow{AB}=\vec{u}$, $\overrightarrow{AC}=\vec{v}$, $\overrightarrow{AD}=\vec{w}$.

$(A, \overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD})$ est-il un repère de l'espace?

$a$ est un nombre réel. On donne les vecteurs $\vec{u}(a;3;3)$ et $\vec{v}(5;-1;2)$.

Trouvez les valeurs de $a$ pour lesquelles :

1. $||\vec{u}||=5.$
2. $||\vec{u}||=||\vec{v}||.$
3. $||\vec{u}+\vec{v}||=\sqrt{30}.$

On donne les points $A(0;1;3)$, $B(\sqrt{2};0;2)$ et $C(\sqrt{2};2;2)$. Quelle est la nature du triangle ABC?

On donne les points $A(5;1;3)$, $B(5;-3;-1)$, $C(1;1;-1)$ et $D(1;-3;3)$.

Démontrez que le tétraèdre ABCD est régulier.

Plan médiateur

Le plan médiateur d'un segment $[AB]$ est le plan perpendiculaire à $[AB]$ en son milieu $I$. C'est donc l'ensemble des points $M$ équidistants de A et de B : $$||\overrightarrow{MA}||=||\overrightarrow{MB}||$$ On donne les points $A(5;2;-1)$ et $B(3;0;1)$.

Indiquez parmi les points suivants ceux qui appartiennent au plan médiateur de $[AB]$.

$C(-2;5;-2)$, $D(1;1;-3)$, $E(3;2;1)$

On donne les points $A(2;1;0)$ et $B(-1;4;2)$.

1. Trouvez le nombre $c$ tel que le point $C(1;1;c)$ soit équidistant de A et de B.
2. M est u point de coordonnées $(x;y;z)$. Démontrez que : "M est un point du plan médiateur de $[AB]$" équivaut à "3x-3y-2z+8=0".

$d$ et $\Delta$ sont deux droites de l'espace définies par : $$d= \left \{ \begin{array}{l} x=3t+2 \\ y=-t-1 \\ z=t+1 \\ \end{array} \right. ,t\in\mathbb{R}\textrm{ et } \Delta \left \{ \begin{array}{c @{=} c} x=s+1 \\ y=2s-3 \\ z=-s+2 \\ \end{array} \right. ,s\in\mathbb{R} $$ Prouvez que ces droites sont sécantes.

La droite $d$ est définie par le point $A(2;-3;5)$ et le vecteur directeur $\vec{u}(1;2;1)$, et la droite $\Delta$ est définie par le point $B(7;2;4)$ et le vecteur directeur $\vec{v}(3;1;-1)$.

Étudiez la position relative de ces deux droites.

Étudiez la position relative des droites : $$d= \left \{ \begin{array}{l} x=1-3t \\ y=1+t \\ z=-3+2t \\ \end{array} \right. ,t\in\mathbb{R}\textrm{ et } d' \left \{ \begin{array}{l} x=6s \\ y=1-2s \\ z=3-4s \\ \end{array} \right. ,s\in\mathbb{R} $$

Que peut-on dire des droites $d$ et $\Delta$ définies ci-dessous? $$d= \left \{ \begin{array}{l} x=1-t \\ y=2+3t \\ z=t \\ \end{array} \right. ,t\in\mathbb{R}\textrm{ et } \Delta \left \{ \begin{array}{l} x=2s \\ y=5-6s \\ z=1-2s \\ \end{array} \right. ,s\in\mathbb{R} $$

La droite $\Delta$ a pour représentation paramétrique : $$\left \{ \begin{array}{l} x=1-3t \\ y=-2+2t \\ z=-1-t \\ \end{array} \right. ,t\in\mathbb{R}$$

1. 1. Déterminez le point I et de $\Delta$ de paramètre 0.
   2. Déterminez un vecteur $\vec{u}$ directeur de $\Delta$.
   3. Justifiez qu'il existe un point de $\Delta$ d'abscisse $-5$.
2. La droite $\Delta$ passe-t-elle par $A(-10; \frac{16}3;-\frac{14}{3})$?

Dans l'espace rapporté à un repère orthonormé $(O;\vec{i}, \vec{j}, \vec{k})$, on considère la droite $\Delta$ de représentation paramétrique $$\left \{ \begin{array}{l} x=t \\ y=1+t \\ z=-2-t \\ \end{array} \right. ,t\in\mathbb{R}$$ $\mathcal{P}(A,\vec{u},\vec{v})$ est le plan passant par $A(0;0;3)$ et dirigé par les vecteurs $\vec{u}=\vec{j}-\vec{k}$ et $\vec{v}=\vec{i}-\vec{j}-\vec{k}$.

$m$ est un réel et $D_m$ est la droite passant par les points $I(1;1;0)$ et $J_m(3;1-m;m)$.

1. Il existe une unique valeur de $m$ pour laquelle les droites $\Delta$ et $D_m$ sont parallèles.
2. Il existe une valeur de $m$ pour laquelle $\Delta$ et $D_m$ sont sécantes.
3. Pour tout $m$ de $\mathbb{R}$, $\Delta$, et $D_m$ sont une intersection vide.
4. Pour tout $m$ de $\mathbb{R}$, $D_m$ coupe le plan $\mathcal{P}(A, \vec{u},\vec{v})$.

La droite $d$ passe par le point $A(0;2;3)$ et est dirigée par le vecteur $\vec{u}(1;1;1)$. La droite $d'$ passe par les points $B(2;0;-1)$ et $C(4;-2;2)$.

Étudiez la position relative de ces deux droites.

On donne les points $A(2;1;0)$ , $B(0;1;1)$ et $C(0;3;2)$.

1. Démontrez que les points A, B,C ne sont pas alignés.
2. Vérifiez que $\overrightarrow{AB}$, $\overrightarrow{AC}$ et $\vec{k}$ ne sont pas coplanaires.
3. La droite passant par O dirigée par $\vec{k}$ coupe le plan $(ABC)$ au point I. Calculez les coordonnées de I.

Équation paramétrique de plan

Le plan $\mathcal{P}$ a pour représentation paramétrique : $$\left \{ \begin{array}{l} x=-2+t+s \\ y=-t+2s \\ z=1+3t-s \\ \end{array} \right. ,t\in\mathbb{R}, s\in\mathbb{R}$$

1. Précisez la position relative du plan $\mathcal{P}$ et du plan $(O;\vec{i};\vec{j})$.
2. Déterminez une représentation paramétrique du plan $\Pi$ passant par $A(1;3;0)$ et parallèle à $\mathcal{P}$
3. Déterminez une représentation paramétrique de la droite $\Delta$ intersection de $\Pi$ et du plan $(O;\vec{i};\vec{j})$.

ABCD est un tétraèdre. J est le milieu de $[BC]$. I et G sont tels que $3\overrightarrow{AI}=\overrightarrow{AB}$ et $3\overrightarrow{JG}=\overrightarrow{JD}$.

A l'aide d'un repère judicieusement choisi, démontrez que la droite $(IG)$ est parallèle au plan $(ADC)$.

Quelle est la position relative de la droite passant par le point $A(-2;5;-3)$ et dirigée par le vecteur $\vec{u}=-2\vec{i}+3\vec{j}$ avec le plan $(O;\vec{i},\vec{j})$?

Une unité de longueur étant choisie dans l'espace, ABCDEFGH est un parallélépipède rectangle tel que $CD=HD=1$ et $BC=2$. I est le milieu de l'arête $[AD]$.

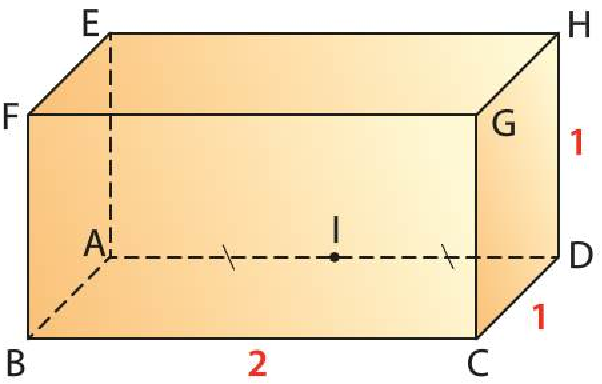
L'espace est muni du repère orthonormé $(A;\overrightarrow{AB},\overrightarrow{AI}, \overrightarrow{AE})$.

1. Quelles sont les coordonnées des points E, H, G?
2. 1. Démontrez que le volume $\mathcal{V}$ du tétraèdre GFIH est égale à $\frac13$.
   2. Démontrez que le triangle FIH est rectangle en I.
   3. En exprimant le volume $\mathcal{V}$ d'une autre manière, calculez la distance du point G au plan $(FIH)$?
3. 1. Donnez une représentation paramétrique du plan $(FIH)$ et de la droite $(AG)$.
   2. Déduisez-en les coordonnées du point K intersection du plan $(FIH)$ et de la droite $(AG)$.
4. On note $\Sigma$ la sphère de centre G passant par K. Le plan $(FIH)$ coupe-t-il la sphère $\Sigma$? Quelle est la nature de l'intersection? Justifiez.

BAC

L'espace est rapporté à un repère orthonormé $(O;\vec{i},\vec{j},\vec{k})$. On donne les points : $A(-1;0;2)$, $B(3;2;-4)$, $C(1;-4;2)$ et $D(5;-2;4)$. I et K sont les milieux respectifs des segments $[AB]$ et $[CD]$. Le point J est tel que $\overrightarrow{BJ}=\frac14\overrightarrow{BC}$.

1. 1. Déterminez les coordonnées des points I, J et K.
   2. Démontrez que ces trois points ne sont pas alignés.
2. On donne les vecteurs $\vec{u}(1;-2;2)$ et $\vec{v}(3;-1;-3)$. Démontrez que les plans $(IJK)$ et $\mathcal{P}(I,\vec{u},\vec{v})$ sont confondus.
3. 1. Déterminez une représentation paramétrique de la droite $(AD)$.
   2. Démontrez que le plan $\mathcal{P}$ et la droite $(AD)$ sont sécants au point L de coordonnées $(\frac12;-\frac12;\frac52)$.
   3. Véridiez que $\overrightarrow{AL}=\frac14\overrightarrow{AD}$.

BAC

L'espace est rapporté à un repère orthonormé $(O;\vec{i},\vec{j},\vec{k})$. Pour chacune des propositions suivantes, indiquez si elle est vraie ou fausse et donnez une démonstration de la réponse choisie.

1. La droite de représentation paramétrique : $$\left \{ \begin{array}{l} x=t+2 \\ y=-2t\\ z=3t-1 \\ \end{array} \right. ,t\in\mathbb{R}$$ est parallèle au plan $\mathcal{P}(A,\vec{u},\vec{v})$ avec $A(3;0;0)$, $\vec{u}(1;-1;1)$ et $\vec{v}(0;1;-2)$.
2. Les droites de représentations paramétriques respectives : $$\left \{ \begin{array}{l} x=2-3t\\ y=1+t \\ z=-3+2t \\ \end{array} \right. ,t\in\mathbb{R} \textrm{ et } \left \{ \begin{array}{l} x=7+2u\\ y=2+2u \\ z=-6-u \\ \end{array} \right. ,u\in\mathbb{R} $$ sont sécantes.
3. On donne les points $A(-1;0;2)$, $B(1;4;0)$ et $C(3;-4;-2)$. Le point $M(x;y;z)$ appartient au plan $(ABC)$ si, et seulement si, $x+z=1$.

BAC

ABCDEFGH est un cube d'arête 1. O est le centre de la face ABCD. L'espace est rapporté au repère orthonormé $(A;\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE})$.

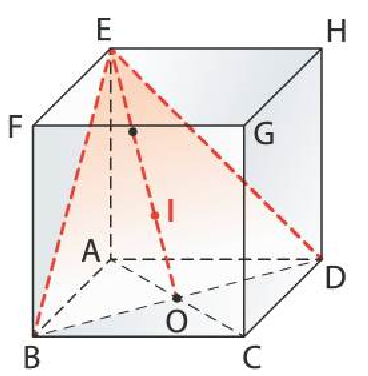
Partie A

1. Démontrez que le triangle BDE est équilatéral.
2. I est le centre de gravité du triangle BDE ( i.e. $\overrightarrow{OI}=\frac13\overrightarrow{OE}$) Calculez les coordonnées de I et démontrez que les points A, I et G sont alignés.

Partie B

Pour tout nombre $k$, $M_k$ est le points de la droite $(AG)$ tel que : $$\overrightarrow{AM_k}=k\overrightarrow{AG}.$$ $\mathcal{P}_k$ est le plan passant par $M_k$ et parallèle au plan $(BDE)$. $N_k$ est le point d'intersection de $\mathcal{P}_k$ et de la droite $(BC)$.

1. 1. A l'aide de la partie A, identifiez : $M_{\frac13}$; $\mathcal{P}_{\frac13}$ et $N_{\frac13}$.
   2. Calculez la distance $M_{\frac13}N_{\frac13}$.
2. 1. Calculez les coordonnées de $M_k$.
   2. Déterminez une représentation paramétrique du plan $\mathcal{P}_k$ et de la droite $(BC)$.
   3. Déduisez-en que $N_k$ a pour coordonnées $(1;3k-1;0)$.
3. Pour quelle valeur de $k$ la distance $M_kN_k$ est-elle minimale? Calculez alors cette distance.

L'espace est rapporté à un repère $(O;\vec{i},\vec{j},\vec{k})$. A a pour coordonnées $(x_0; y_0; z_0)$. B est un point distinct de A. On pose$\vec{u}=\overrightarrow{AB}$ avec $\vec{u}$ de coordonnées $(a;b;c)$.

1. Justifiez l'équivalence suivante : $$M(x;y;z)\in[AB] \textrm{, équivaut à :}$$ $$(S)=\left \{ \begin{array}{l} x=x_0+at\\ y=y_0+bt \\ z=z_0+ct \\ \end{array} \right. ,t\in[0;1].$$
2. Justifiez l'affirmation suivante : "Pour traduire l'appartenance de M à la demi-droite $[AB)$, il suffit de remplacer $t\in[0;1]$ par $t\in[0;+\infty[ $ dans le système (S)."

L'espace est rapporté à un repère $(0;\vec{i},\vec{j},\vec{k})$. Trouvez la nature géométrique de chacun des ensembles suivants : $$\mathcal{E}_1=\left \{ \begin{array}{l} x=2t+1\\ y=3t \\ z=t+1 \\ \end{array} \right. ,t\in[0;1]$$ $$\mathcal{E}_2=\left \{ \begin{array}{l} x=1+t\\ y=2+t \\ z=-1+2t \\ \end{array} \right. ,t\in[-1;0]$$ $$\mathcal{E}_2=\left \{ \begin{array}{l} x=3t-1\\ y=t+2 \\ z=t-2 \\ \end{array} \right. ,t\in[0;+\infty[ $$