Produit scalaire dans l'espace et vecteurs orthogonaux.

Soit $\vec{u}$ et $\vec{v}$ deux vecteurs de l'espace et A,B et C trois points de l'espace tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$. On appelle produit scalaire de $\overrightarrow{u}$ et $\overrightarrow{v}$ le nombre réel, noté $\overrightarrow{u}.\overrightarrow{v}$, défini ainsi :

Soit $\vec{u}$, $\vec{v}$ et $\vec{w}$ trois vecteurs de l'espace et $k$ un réel.

$$\begin{array}{ll} \textrm{(1) } \vec{u}.\vec{u}=||\vec{u}||^2 & \textrm{(2) }(k\vec{u}).\vec{v}=(\vec{u}).k\vec{v}=k(\vec{u}.\vec{v})\\ \textrm{(3) } \vec{u}.\vec{v}=\vec{v}.\vec{u}&\textrm{(4) }||\vec{u}+\vec{v}||^2=||\vec{u}||^2+2\vec{u}.\vec{v}+||\vec{v}||^2\\ \textrm{(5) } \vec{u}.(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}&\textrm{(5) } \vec{u}^2-\vec{v}^2=(\vec{u}+\vec{v}).(\vec{u}-\vec{v})\\ \end{array}$$

Vecteurs orthogonaux

Deux vecteurs $\vec{u}$ et $\vec{v}$ de l'espace sont orthogonaux si et seulement si $\vec{u}.\vec{v}=0$.

Deux droites $\mathcal{D}$ et $\Delta$ de vecteurs directeurs respectifs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont dites orthogonales lorsque $\overrightarrow{u}$ et $\overrightarrow{v}$ le sont.

$\vec{0}$ est orthogonal à tout vecteur de l'espace.

ABCDEFGH est un cube de coté a, O le milieu de $[DF]$.

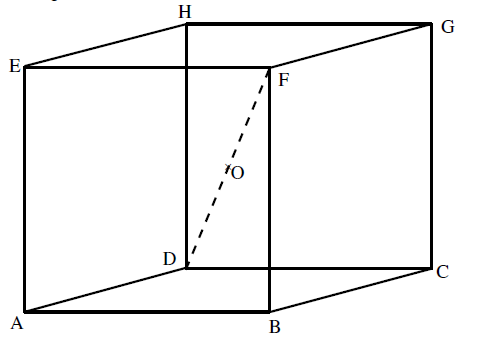
Déterminer $\overrightarrow{AB}.\overrightarrow{EG}$, $\overrightarrow{AB}.\overrightarrow{AG}$,$\overrightarrow{BC}.\overrightarrow{DE}$ et $\overrightarrow{AB}.\overrightarrow{AO}$

Expression analytique.

Soit $\vec{u}(x;y;z)$ et $\vec{v}(x';y';z')$ dans une base orthonormale $(O,\vec i,\vec j,\vec k)$ de l'espace, alors :

$$\vec{u}.\vec{v}=xx'+yy'+zz'$$

Soit $\vec{u}(x;y;z)$ et $\vec{v}(x';y';z')$ dans une base orthonormale $(O,\vec i,\vec j,\vec k)$.

$\vec u.\vec v=(x\vec i+y\vec j+z\vec k).(x'\vec i+y'\vec j+z'\vec k)=xx'\vec i^2+yy'\vec j^2+zz'\vec k^2=xx'+yy'+zz'$ car la base est orthonormale

Soient deux points $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ dans un repère orthonormal de l'espace. Alors : $$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$$

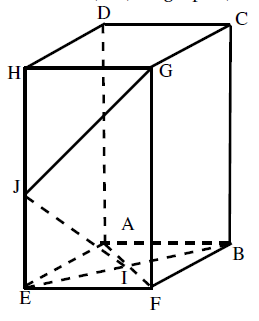
ABCDEFG est un parallélépipéde rectangle tel que : $AB=AE=2$ et $AD=4$.

I est le centre du carré ABEF et J est le milieu de $[EH]$.

Déterminer, à 0,1 degré près, la mesure de l'angle géométrique $\widehat{IJG}$.

Orthogonalité et équation cartésienne de plan de l'espace.

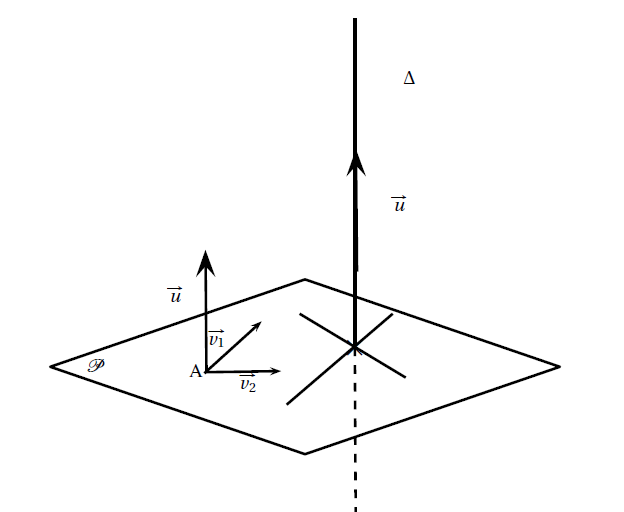
On rappelle qu'une droite $\Delta$ est perpendiculaire à un plan $\mathcal{P}$ si et seulement s'il existe deux droites sécantes du plan perpendiculaires à $\Delta$. Autrement dit si $\overrightarrow{u}$ est un vecteur de $\Delta$ et $(A;\overrightarrow{v_1};\overrightarrow{v_2})$ un repère de $\mathcal{P}$, on a : $$ \Delta \bot \mathcal{P} \Longleftrightarrow \overrightarrow{u}.\overrightarrow{v_1}=0 \textrm{ et } \overrightarrow{u}.\overrightarrow{v_2}=0$$

Equation cartésienne d'un plan.

Tout vecteur non nul orthogonal à deux vecteurs non colinéaires de $\mathcal{P}$ est appelé vecteur normal au plan $\mathcal{P}$.

Un vecteur normal à un plan $\mathcal{P}$ est orthogonal à tous les vecteurs du plan $\mathcal{P}$.

Caractérisation d'un plan.

Soit $\vec{n}$ un vecteur non nul et A un point de l'espace, l'ensemble des points M de l'espace tels que $\vec{n}.\vec{AM}=0$ est le plan $\mathcal{P}$ passant par A et de vecteur normal .

On considère $\mathcal{D}$ la droite passant par A et de vecteur directeur $\vec{n}$ et $\mathcal{P}$ le plan passant par A et de vecteur normal $\vec n$.

M un point de $\mathcal{P}$, alors $\overrightarrow{AM}$ est un vecteur de $\mathcal{P}$, d'où $\vec{n}.\overrightarrow{AM}=0$.

Réciproquement soit M tel que $\vec{n}.\overrightarrow{AM}=0$. On note H le projeté orthogonal de M sur la droite $\mathcal{D}$, alors $\vec{n}.\overrightarrow{AM}=\vec{n}.\overrightarrow{AH}=0$.

Or $\overrightarrow{AH}$ et $\vec{n}$ sont colinéaires donc $\vec{n}.\overrightarrow{AH}=0$ donne $\overrightarrow{AH}=\vec{0}$ d'où $A=H$.

Ainsi le projeté orthogonal de M sur $\mathcal{D}$ est le point A. Donc M appartient à $\mathcal{P}$.

Tout plan de vecteur normal $\vec{n}(a;b;c)$ admet une équation cartésienne de la forme $ax+by+cz+d=0$ où $d\in\mathbb{R}$.

Réciproquement, l'ensemble des points $M(x;y;z)$ tels que $ax+by+cz+d=0$ (avec a,b, et c non nuls en même temps) est un plan de vecteur normal $\vec{n}(a;b;c)$.

Soit $A(x_A;y_A;z_A)$ un point du plan $\mathcal{P}$ et $\vec{n}(a;b;c)$ un vecteur normal au plan $\mathcal{P}$.\\ $M(x;y;z)\in\mathcal{P}$ $\Leftrightarrow$ $\vec{n}.\overrightarrow{AM}=0$ $\Leftrightarrow$ $a(x-x_A)+b(y-y_A)+c(z-z_A)=0$\\ $\Leftrightarrow$ $ax+by+cz+d=0$ où $d=-ax_A-by_A-cz_A$.

$\vec{n}$ étant normal , il est non nul et donc a,b et c sont également non nul en même temps.

Réciproquement, comme a,b et c non nul en même temps, prenons $a\ne0$ et considérons $A(-\frac{d}{a};0;0)$. A vérifie bien la relation de l'énoncé.

Soit $M(x;y;z)$ vérifiant $ax+by+cz+d=0$. $\vec{n}.\overrightarrow{AM}=a(x+\frac{d}{a})+by+cz=ax+by+cz+d=0$.

Ainsi $M(x;y;z)$ vérifiant $ax+by+cz+d=0$ $\Leftrightarrow$ $\vec{n}.\overrightarrow{AM}=0$.

Donner une equation cartésienne du plan $(ABC)$ où $A(1;1;1)$, $B(-2;2;1)$, et $C(1,0,2)$.

Soit $\mathcal{P}$ et $\mathcal{P}'$ deux plans distincts de vecteurs normaux $\vec{n}(a;b;c)$ et $\vec{n'}(a';b';c')$ respectivement.

$\mathcal{P}$ et $\mathcal{P}'$ sont parallèles si et seulement si $\vec{n}$ et $\vec{n'}$ sont colinéaires.

$\mathcal{P}$ et $\mathcal{P}'$ sont perpendiculaires si et seulement si $\vec{n}.\vec{n'}=0$.

>
  1. Montrer que les plans d'équations cartésiennes $x+y-5z+1=0$ et $2x+2y-10z-3=0$ sont paralléles.
  2. Les plans d'équations cartésiennes $x+y-5z+1=0$ et $5x+z-3=0$ sont perpendiculaires.

Exercices

Produit scalaire

On donne les vecteurs $\vec{u}$ et $\vec{v}$ de coordonnées respectives $(1;\sqrt{3};0)$ et $(0;-\sqrt{3};1)$.

  1. Calculez $\vec{u}.\vec{v}$.
  2. Quelle est,à un degré près, la mesure de l'angle géométrique associé à $\vec{u}$ et $\vec{v}$?

On donne $A(2;-1;3)$, $B(1;0;-1)$ et $C(0;-1;2)$. Quelle est, à un degré près, a mesure de $\hat{BAC}$?

$\vec{u}$ et $\vec{v}$ sont deux vecteurs tels que : $$||\vec{u}||=5; ||\vec{v}||=3 \textrm{ et } \vec{u}.\vec{v}=-4$$ Calculez

  1. $2\vec{u}.(\vec{v}-3\vec{u})$
  2. $(\vec{u}+\vec{v}).(\vec{u}-3\vec{v})$

SABCD est une pyramide régulière, ABCD est un carré de centre O. Toutes les arêtes de centre O. Toutes les arêtes ont pour longueur $a$.

Calculez en fonction de $a$ :

  • $\overrightarrow{SA}.\overrightarrow{SB}$
  • $\overrightarrow{SA}.\overrightarrow{SC}$
  • $\overrightarrow{AS}.\overrightarrow{AC}$

    • $\mathcal{P}$ est le plan défini par les droites $d_1$ et $d_2$, sécantes en A et de vecteurs directeurs $\vec{u_1}$ et $\vec{u_2}$.

    $\Delta$ est la droite passant par A et de vecteur directeur un vecteur $\vec{n}$ orthogonal aux vecteurs $\vec{u_1}$ et $\vec{u_2}$.

    Démontrez que $\Delta$ est orthogonale à toute droite $d$ du plan $\mathcal{P}$

    les vecteurs $\vec{u}(\frac54;-\frac32; \frac12)$ et $\vec{v}(-\frac25;2;3)$ sont-ils orthogonaux?

    On donne les points : $A(2;-5;1)$ , $B(0;2;6)$ et $C(-2:3:1)$.

    Démontrez que la droite $d$ passant par C et de vecteur directeur $\vec{u}(-4;1;-3)$ est orthogonale à la droite $(AB)$.

    ABCDEFGH est un cube d'arête 1. Les points I et J sont tels que : $$3\overrightarrow{AI}=\overrightarrow{AB}\textrm{ et }3\overrightarrow{BJ}=\overrightarrow{BC}.$$

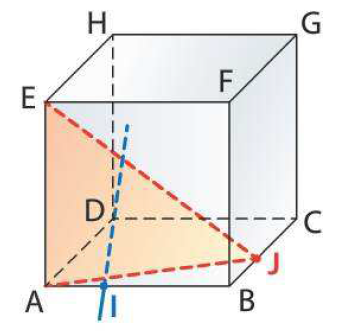
    1. Démontrez que les droites $(DI)$ et $ (AJ)$ sont perpendiculaires.
    2. Déduisez-en que la droite $(DI)$ est perpendiculaire au plan $(AJE)$.

    ABCDEFGH est un cube d'arête 1. Le point I est le milieu de $[HD]$ et le point O est le centre de la face EFGH. On se propose de démontrer de deux manières différentes que la droite $(AO)$ est perpendiculaire au plan $(ECI)$.

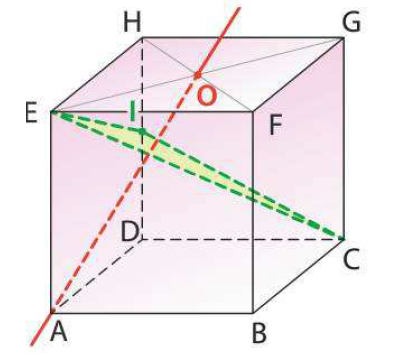
    1. Avec un repère

      On choisit le repère orthonormé $(D;\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DH})$.

      1. Quelles sont les coordonnées des points A, E, I, O, C?
      2. Calculez $\overrightarrow{AO}.\overrightarrow{EC}$ et $\overrightarrow{AO}.\overrightarrow{EI}$. Concluez.
    2. sans repère
      1. En écrivant que $\overrightarrow{AO}=\overrightarrow{AE}+\overrightarrow{EO}$ et $\overrightarrow{EC}=\overrightarrow{EG}+\overrightarrow{GC}$, calculez $\overrightarrow{AO}.\overrightarrow{EC}$.
      2. En utilisant la relation de Chasles, calculez $\overrightarrow{AO}.\overrightarrow{EI}$. Concluez.

    Equation de plan

    Déterminez, dans chaque cas, une équation cartésienne du plan $\mathcal{P}$ passant par A et de vecteur normal $\vec{n}$.

    1. $A(2;0;1)$ et $\vec{n}(1;-1;3)$.
    2. $A(\sqrt{2};-2;5)$ et $\vec{n}(2;-3;-1)$

    Déterminez, dans chaque cas, une équation cartésienne du plan $\mathcal{P}$ perpendiculaire en A à la droite $(AB)$.

    1. $A(2;0;-1)$ et $B(0;1;3)$.
    2. $A(\sqrt{2};-2;5)$ et $B(-1;3;2)$.

    Le plan $\mathcal{P}$ a pour équation cartésienne : $$3x+2y-5=0.$$ Les points A et B ont pour coordonnées respectives $(1;2;1)$ et $(\frac52;3;1)$.

    La droite $(AB)$ est-elle orthogonale au plan $\mathcal{P}$?

    Le plan $\mathcal{P}$ a pour équation cartésienne $x-3y+2z-5=0$ et le point A a pour coordonnées $(2;3;-1)$. Est-il vrai que le point $H(3;0;1)$ est le projeté orthogonal de A sur le plan $\mathcal{P}$?

    On donne le point A de coordonnées $(1;-1;2)$ et le vecteur directeur $\vec{u}=-\vec{i}+2\vec{j}+3\vec{k}$.

    Quelle est la nature de l'ensemble des point $M(x;y;z)$ tels que $\overrightarrow{AM}.\vec{u}=5$?

    On donne les points : $$A(3;-2;1), B(5;2;-3) \textrm{ et } C(6;-2;-2).$$

    1. Vérifiez que les points A,B,C ne sont pas alignés, et que $\vec{n}(2;1;2)$ est un vecteur normal au plan $(ABC)$.
    2. Déduisez-en une équation cartésienne du plan $(ABC)$.

    ABCDEFGH est un cube d'arête 1. Les points M, N P sont tels que : $$3\overrightarrow{AM}=2\overrightarrow{AB};3\overrightarrow{AN}=2\overrightarrow{AD}; 3\overrightarrow{CP}=2\overrightarrow{CG}.$$ On définit le repère orthonormé $(B;\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{BF})$.

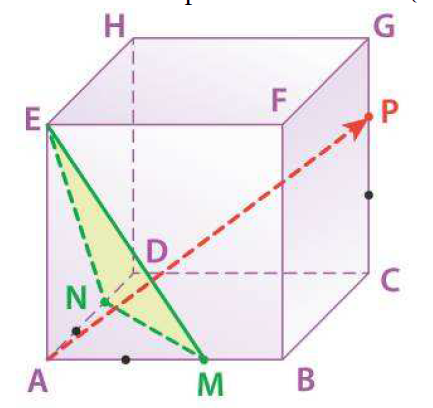
    1. Démontrez que $\overrightarrow{AP}$ est normal au plan $(EMN)$.
    2. Déduisez-en une équation cartésienne du plan $(EMN)$.

    Position relative : droite/plan

    Les points A et B ont respectivement pour coordonnées $(2;1;-1)$ et $(3;0;0)$. A tout nombre m, on associe le plan $\mathcal{P_m}$ d'équation cartésienne : $$mx+y+mz+m-1=0.$$ Pour chaque affirmation , dites si elle est vraie ou fausse. Justifiez.

    1. Pour tout m, la droite $(AB)$ est incluse dans $\mathcal{P_m}$.
    2. Il existe une valeur de m pour laquelle la droite $(AB)$ est perpendiculaire à $\mathcal{P_m}$.
    3. Pour tout m, la droite $(AB)$ et le plan $\mathcal{P_m}$ sont sécants.
    4. Il existe une valeur de m et une seule pour laquelle $\mathcal{P_m}$ est parallèle à la droite $(AB)$.

    Deux cubes d'arête 1 sont disposés comme l'indique la figure. L'espace est rapporté au repère orthonormé $(D;\overrightarrow{DA}, \overrightarrow{DC}, \overrightarrow{DH})$. Le point I est le milieu de $[EF]$.

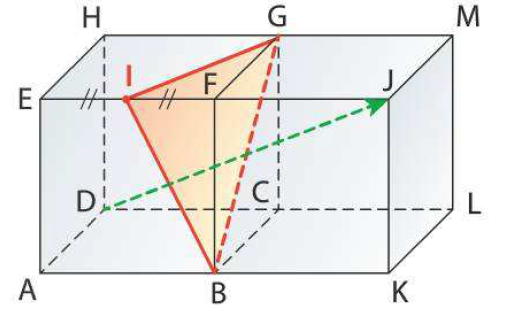
      1. Démontrez que $\overrightarrow{DJ}$ est normal au plan $(BIG)$.
      2. Déduisez-en une équation cartésienne au plan $(BIG)$.
      1. Déterminez une représentation paramétrique de la droite $\Delta$ passant par F et perpendiculaire au plan $(BIG)$.
      2. La droite $\Delta$ coupe le plan $(BIG)$ en L.Le point L est-il l'orthocentre de BIG?

    Position relative : plan/plan

    1. $\Delta$ est la l'intersection des plans $\mathcal{P}_1$ et $\mathcal{P}_2$ d'équations respectives : $$x-y+z-3=0 \textrm{ et } 2x+z=0.$$ Donner une représentation paramétrique de $\Delta$.
    2. Déterminez les coordonnées du point d'intersection de $\Delta$ et du plan $\mathcal{R}$ d'équation $x+y-z=0$.(Si ce point existe).

    La droite $\Delta$ est l'intersection des plans $\mathcal{P}_1$et $\mathcal{P}_2$ d'équations respectives :$$2x-y+5=0 \textrm{ et } 3x+y-z=0.$$ La droite $\Delta$ est-elle parallèle au plan $\mathcal{Q}$ d'équation $5x-5y+z=0$?

    Les plans $\mathcal{P}_1$ et $\mathcal{P}_2$ ont pour équations respectives : $$x+2y-z+1=0 \textrm{ et } x-y-z=0$$

    1. Démontrez que ces plans sont perpendiculaires.
    2. Donnez une représentation paramétrique dela droite $\Delta$, intersection de ces deux plans.
    3. A est le point de coordonnées $(0;1;1)$. Comme dans le plan, la distance d'un point A à la droite $\Delta$ est la distance AH où H est le point d'intersection de la droite $\Delta$ et de la perpendiculaire à $\Delta$ passant par A.
      1. Trouvez une représentation paramétrique de la droite $d_1$ passant par A et perpendiculaire à $\mathcal{P}_1$.
      2. Trouvez une représentation paramétrique de la droite $d_2$ passant par A et perpendiculaire à $\mathcal{P}_2$.
      3. Déduisez-en les coordonnées des points $H_1$ et $H_2$, intersections respectives de $d_1$ avec $\mathcal{P}_1$ et de $d_2$ avec $\mathcal{P}_2$.
      4. Calculez $AH_1$ et $AH_2$.Déduisez en la distance de A à $\Delta$.

    Synthèse

    Bac

    OABCDEFH est un cube d'arête 1. $\overrightarrow{OP}=2\overrightarrow{OA}$, $\overrightarrow{OQ}=4\overrightarrow{OC}$ et $\overrightarrow{BR}=2\overrightarrow{BC}$. L'espace est muni du repère orthonormé $(O,\overrightarrow{OA},\overrightarrow{OC},\overrightarrow{OD})$.

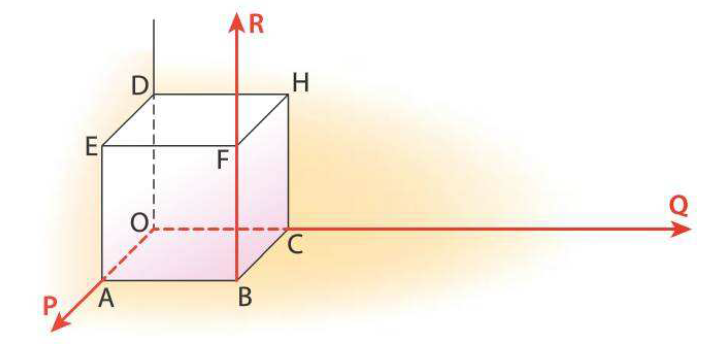
      1. Quelle est la nature de PQR?
      2. Vérifiez que le plan $(PQR)$ a pour équation : $$4x+2y+z-8=0.$$
    1. Soit H le projeté orthogonal de D sur le plan $(PQR)$.
      1. Trouvez une représentation paramétrique de la droite $(DH)$.
      2. Déduisez-en les coordonnées de H.
      3. Démontrez que H est une point de la droite $(PR)$.

    Pour chaque question , une seule réponse est exacte. Indiquez la bonne réponse en justifiant. L'espace est muni d'un repère orthonormé $(O;\vec{i},\vec{j},\vec{k})$. On donne les points $A(1;2;-4)$, $B(-3;4;1)$, et la plan $\mathcal{P}$ d'équation $2x+3y-z+4=0$.

    1. $$\left \{ \begin{array}{l} x=-8+2t\\ y=7-t\\ z=6+t\\ \end{array} \right. ,t\in\mathbb{R} $$
      1. le plan $\mathcal{P}$ et la droite $d$ sont sécantes.
      2. $\mathcal{P}$ et $d$ n'ont aucun point commun.
      3. La droite $d$ est incluse dans le plan $\mathcal{P}$.
    2. $\mathcal{P}'$ est le plan d'équation $x+4y-3z+4=0$.
      1. $\mathcal{P}$ et $\mathcal{P}'$ sont parallèles et distincts.
      2. $\mathcal{P}$ et $\mathcal{P}'$ sont confondus.
      3. $\mathcal{P}$ et $\mathcal{P}'$ sont sécants suivant une droite de vecteur $-\vec{i}+\vec{j}+\vec{k}$.
      4. aucune des réponses précédentes.
    3. Le plan médiateur du segment $[AB]$ a pour équation :
      1. $-4x+2y+5z-\frac52=0$
      2. $-4x+2y+5z+\frac52=0$
      3. Aucune des réponses précédentes n'est exacte.

    ABCDEFGH est un cube d'arête 1. I est l'intersection de la droite $(EC)$ et du plan $(AFH)$. L'espace est muni du repère orthonormé $(D;\overrightarrow{DA},\overrightarrow{DC},\overrightarrow{DH})$.

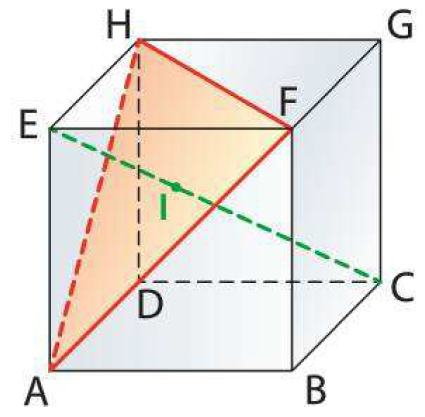
    1. Déterminer
      1. une représentation paramétrique de la droite $(EC)$;
      2. une équation cartésienne du plan $(AFH)$.
    2. Déduisez-en les coordonnées de I et démontrez que la droite $(EI)$ est perpendiculaire au plan $(AFH)$.
      1. Démontrez que la droite $(IH)$ est perpendiculaire à la droite $(AF)$.
      2. Que représente I pour le triangle AFH?
    4. Dans cette question, toute trace de recherche même incomplète ou d'initiative non fructueuse sera prise en compte.
      Un tétraèdre est de type 1 si toutes ses faces ont la même aire.
      Un tétraèdre est de type 2 si toutes ses arêtes opposées sont orthogonales deux à deux.
      Un tétraèdre est de type 3 s'il est à la fois de type 1 et de type 2.
      Précisez le type de EAFH.

    Bac

    L'espace est muni d'un repère orthonormé $(O,\vec{i},\vec{j},\vec{k})$.

    Le plan $\mathcal{P}$ a pour équation $ax+by+cz+d=0$ et on note $\vec{n}(a,b,c)$ un vecteur norma à $\mathcal{P}$.

    Le point $A(x_0;y_0;z_0)$ se projette en $H(\alpha,\beta,\gamma)$ sur le plan $\mathcal{P}$.

    1. La droite $(AH)$passe par A et a pour vecteur directeur $\vec{n}$.
      1. Les vecteurs $\vec{n}$ et $\overrightarrow{AH}$ sont colinéaires.
        Déduisez-en que $\vec{n}.\overrightarrow{AH}|=||\vec{n}||\times AH$, puis que $\vec{n}.\overrightarrow{AH}|=\sqrt{a^2+b^2+c^2}\times AH$.
        1. En utilisant la forme analytique du produit sclaire, démontrer que $$|\vec{n}.\overrightarrow{AH}|=|a\alpha+b\beta+c\gamma-ax_-by_0-cz_0|.$$
        2. Justifier que $a\alpha+b\beta+c\gamma=-d.$
        3. Déduisez-en que : $$AH\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}.$$ AH est la distance du point A au plan $\mathcal{P}$.
    2. Application

      ABCDEFGH est un cube d'arête 1.

      I est le milieu de l'arête $[HD]$ et O est le centre de la face ABCD? L'espace est muni d'un repère $(A;\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE})$.

      1. Vérifiez que le plan $(AGI)$ a pour équation $x+y-2z=0$ et que le vecteur $\overrightarrow{OE}$ est un vecteur normal à ce plan.
      2. Dans cette question, on se propose de calculer de trois manières la distance du point E au plan $(AGI)$.
        1. Manière 1 : A l'aide de la formue établie dans la partie A, démontrez que la distance de E au plan $(AGI)$ est égale à $\frac{\sqrt{6}}{3}$.
        2. Manière 2 :
          Déterminez une représentataion paramétrique de la droite $(OE)$.\\ Déduisez-en les coordonnées au point K d'intersection de la droite $(OE)$ et du plan $(AGI)$.
          Calculez alors la distance EK.
        3. Manière 3 :
          Calculez l'aire du triangle EAI et déduisez-en que le volume de GAEI est égale à $\frac16$.
          Calculez l'aire du triangle AGI et déduisez-en la distance du point E au plan $(AGI)$.
    Licence Creative Commons
    Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.