Echantillonnage
Propriété de la variable aléatoire fréquence $F_n$.
Soit $X_n$ une variable aléatoire qui suit la loi binomiale $B(n; p)$; on définit la variable aléatoire $F_n$ par $$F_n=\frac{X_n}{n}$$ elle représente la fréquence de succès pour un schéma de Bernoulli de paramètre n et p.
L'intérêt de cette variable est qu'elle est comprise en 0 et 1, alors qu'une variable du type $X_n$ est comprise entre 0 et n.
La variable aléatoire $F_n$ ne suit pas une loi binomiale ; néanmoins, sa loi de probabilité et la représentation graphique de cette loi se déduisent directement de celles de $X_n$.
Si $X_n$ est une variable aléatoire suivant une loi binomiale $B(n; p)$, alors,pour tout $\alpha$ dans $]0; 1[$, on a : $$\lim\limits_{n\to +\infty}P(\frac{X_n}{n}\in I_n)=1-\alpha,$$ où $$I_n=[p-u_{\alpha}\frac{\sqrt{p(1-p)}}{\sqrt{n}};p+u_{\alpha}\frac{\sqrt{p(1-p)}}{\sqrt{n}}]$$
Rappelez vous que lorsqu'on choisit une valeur $\alpha$, le nombre noté $u_{\alpha}$ est tel que : $$P(u_{\alpha}\leq Z\leq u_{\alpha}) = 1-\alpha,$$où Z est une variable aléatoire suivant la loi normale centrée réduite.
Rappelez vous aussi que : $P(u_{\alpha} \leq Z\leq u_{\alpha}) =\int_{-u_{\alpha}}^{u_{\alpha}}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} dx$
Intervalle de fluctuation asymptotique
Le paragraphe précédent permet de déterminer efficacement un intervalle regroupant environ 95% des valeurs pour la variable aléatoire $Z_n$, en approximant cette variable aléatoire par la loi normale.
L'intervalle $$[p-u_{\alpha}\frac{\sqrt{p(1-p)}}{\sqrt{n}};p+u_{\alpha}\frac{\sqrt{p(1-p)}}{\sqrt{n}}]$$ est un \textbf{intervalle de fluctuation asymptotique au seuil de confiance $1-\alpha$} de la variable aléatoire $F_n$ qui, à tout échantillon de taille n, associe la fréquence obtenue.
Cet intervalle contient $F_n$ avec une probabilité d'autant plus proche de $1-\alpha$ que n est grand.
Cette approximation est valable dès que $n > 30$, $np > 5$ et $n(1-p) > 5$.
Dans un casino, il a été décidé que les "machine à sous" doivent être réglées sur une fréquence de gain du joueur de $g=0,06$. Une fréquence inférieur est supposée faire "fuir le nigot", et une fréquence supérieure est susceptible de ruiner le casino.
Trois contrôleurs différents vérifient une même machine.
Le premier a joué 50 fois et gagné 2 fois, le second a joué 120 fois et gagné 14 fois, le troisième a joué 400 fois et gagné 30 fois.
En utilisant des intervalles de fluctuation asymptotique au seuil de 95%, examiner dans chaque cas la décision à prendre par le contrôleur, à savoir accepter ou rejeter l'hypothèse $g=0,006$.
estimation d'une proportion
Le problème de l'estimation peut être considéré comme le problème « inverse » de celui de l'échantillonnage : à partir de la fréquence f observée sur un échantillon, on cherche à estimer la proportion p correspondante dans la population toute entière. C'est le problème que l'on cherche à résoudre en réalisant des sondages.
Si la variable aléatoire $X_n$ suit la loi $B(n;p)$, alors pour tout réel $p$ de $]0;1[$, il existe un entier $n_0$ tel que si $n\geq n_0$ alors $$P(p-\frac{1}{\sqrt{n}}\leq \frac{X_n}{n}\leq p+\frac{1}{\sqrt{n}})>0,95$$
On observe une fréquence $f_{obs}$ sur un échantillon de taille $n$. On appelle \textbf{intervalle de confiance de p au niveau de confiance de 95\%} l'intervalle : $$[f_{obs}-\frac{1}{\sqrt{n}};f_{obs}+\frac{1}{\sqrt{n}}]$$
On dispose d'une urne contenant un très grand nombre de boules rouges et bleues. On ignore quelle est la proportion p de boules rouges dans l'urne.
On réalise un tirage de 100 boules. On obtient 59 rouges. Quel est l'intervalle de confiance de la fréquence des boules rouges au niveau de confiance de $95%$.
Exercices
Echantillonnage
Un sondage auprès de 900 consommateurs d'une grande marque M montre que 774 en sont satisfaits. Par ailleurs, un publicité affirme que $90\%$ des consommateurs de M en sont satisfaits. On fait l'hypothèse que la proportion de consommateurs satisfaits de la marque M est $p=0,9$.
- Démontrez que les trois conditions d'approximations sont vérifiées.
- Déterminez l'intervalle de fluctuation I à $95\%$ de la fréquence de consommateurs satisfaits de M sur un échantillon aléatoire de taille 900.
- Pouvez-vous affirmer qu'au seuil de risque de $5\%$, les résultats du sondage sont en accord avec l'annonce publicitaire?
L'Institut National de Prévention et d'Education pour la Santé (INPES) a étudié la proportion de fumeurs quotidiens de tabac en France en 2010. Chez les 15-19ans, $26\%$ des garçons et $20\%$ des filles sont des fumeurs quotidiens.
Sur un échantillon de 1000 provinois de cette tranche d'âge, dont 450 sont des filles, on a dénombré 178 fumeurs quotidiens chez les garçons et 98 chez les filles.
On fait l'hypothèse que dans le bassin provinois., la proportion de fumeurs quotidiens chez les 15-19ans est de $26\%$ pour les garçons et $20\%$ pour les filles.
Répondez aux questions suivantes pour les garçons puis pour les filles.
- Vérifiez les trois conditions d'application de la règle de décision.
- Déterminez pour un tel sondage l'intervalle de fluctuation I à $95\%$ de la fréquence de fumeurs quotidiens chez les 15-19ans.
- Pouvez-vous considérer, au seuil de risque de $5\%$, que la fréquence observée de jeunes fumeurs quotidiens provinois dans cet échantillon est en accord avec la proportion de jeunes fumeurs quotidiens de la population française.
Dans un lycée, la moyenne de mathématiques d'un élève de terminale S pris au hasard est une variable aléatoire qui suit approximativement la loi $\mathcal{N}(10,5;6,25)$.
Le proviseur de ce lycée dit alors : "Environ deux tiers des élèves de TS ont une moyenne de mathématiques situées entre 8 et 13".
A-t-il raison? Justifiez.
La longueur d'un saut (en mètre) d'un kangourou adulte peut être modélisée par une variable aléatoire qui suit la loi $\mathcal{N}(\mu;\sigma^2)$.
On sait qu'environ $95\%$ des sauts d'un kangourou adulte mesurent entre 2 mètres et 10 mètres de long.
-
- En supposant que l'intervalle de longueur, donné dans l'énoncé, en centré sur l'espérance $\mu$, précisez les valeurs de $\mu$ et de $\sigma$ ( à $10^{-2}$ près).
- Déduisez-en un intervalle de longueur ( au cm près) correspondant à environ $99\%$ des sauts d'un kangourou adulte.
-
- On a pu observer, chez les kangourou adultes, des longueurs de saut dépassant les 13 mètres. Calculez à $10^{-4}$ près la probabilité d'un tel événement.
- Si l'on considère qu'un kangourou adulte effectue 10000 sauts par jour, estimez alors le nombre quotidien de sauts dépassant 13 mètre de long.
Dans chacune des situations suivantes, déterminez l'espérance et l'écart-type de la fréquence de succés,puis, si les conditions d'approximation sont remplies, précisez la loi normale approchant la loi de la fréquence de succès.
- Fréquence d'apparition de Pile au terme de 400 lancers d'une pièce équilibrée.
- Fréquence de l'événement "Obtenir une figure" au terme de 100 tirages au hasard et avec remise d'une carte d'un jeu de 32 cartes
- Fréquence de l'événement "Somme des résultats des deux dés supérieure ou égale à 9" au terme de dix lancers de dés cubiques parfaits.
Woburn est une petite ville industrielle du Massachussetts, au Nord-Est des Etat unis. DAns les années 70, la communauté locale s'émeut du grand nombre d'enfants atteints de leucémie dans certains quartiers de la ville : entre 1969 et 1979, on a observé douze cas de leucémie sur un échantillon de 11748 enfants de moins de 14 ans.
A cette même époque, au Etats-unis, la proportion p de leucémies chez les enfants de moins de 14 ans est 0,00045. On fait l'hypothèse qu'à Woburn, la proportion théorique de leucémies chez les enfants de moins de 14 ans est la même que celle des Etat-Unis.
- Vérifiez que les trois conditions d'application de la règle de prise de décision sont remplies.
- Déterminez les intervalles de fluctuation (centrée en p ) à $95\%$ et à $99\%$ de la fréquence de leucémies sur un échantillon aléatoire de 11748 enfants de moins de 14 ans. Ecrivez les bornes de ces intervalles avec cinq décimales.
- Peut-on considérer, au seuil de risque de $5\%$, que la fréquence observée de leucémies chez les enfants de moins de 14 ans à Woburn, dans cet échantillon, est en accord avec la proportion de leucémies chez les enfants de moins de 14 ans dans la population américaine?
- Même question mais au seuil de $1\%$
Une enquête conduite par le Département de Santé Public du Massachusetts en 1981 confirmera que les sols de Woburn ont été contaminés par des résidus de tanneris et de produits chimiques. Les industriels concernés seront condamnés et la dépollution des sites engagée. C'est l'exposition in utérin à cette eau contaminée qui serait à l'origine des cas de leucémies observés.
Un salon du tourisme a permis à 200 visiteurs , tirés au sort, de jouer pour gagner un séjour au Sri Lanka. Le jeu est simple : une roue de loterie se met à tourner de manière automatique puis s'arrête au bout d'un moment. Si le secteur de la roue correspondant au séjour, d'angle au centre 18°, est désigné par le pointeur, alors c'est gagné! Sur les 200 joueurs, il y a deux gagnants.
-
Quelle est la valeur de p?
Vérifiez que les trois conditions d'approximation permettant une prise de décision sont remplies.
Déterminez l'intervalle de fluctuation I ( centré en p) à $95\%$ de la fréquence de gagnants sur un échantillon aléatoire de taille 200. Écrivez les bornes de I avec trois décimales.
- Compte tenu du nombres de gagnants observé, accepte-t-on au seuil de risque de $5\%$ l'hypothèse formulée dans l'énoncé?
- Entre quelles valeurs aurait du se situer le nombre de gagnants pour qu'on accepte l'hypothèse de l'énoncé?
Estimation
Deux candidats (M. Legrand et M. Lepetit) se présentent à une élection.
Le dernier sondage effectué auprès d'un échantillon aléatoire de 400 personnes donne M. Legrand gagnant à $54\%$.
M. Lepetit affirme alors : "Ce sondage rend ma victoire plausible ! "
- Déterminez, à partir de cette étude , la fourchette à $95\%$ de confiance de la proportion de personnes envisageant de voter pour M. Lepetit.
- A partir de cette fourchette, commentez l'affirmation de ce candidat.
Lors d'un sondage réalisé début 2010 auprès d'un échantillon aléatoire de 1000 personnes inscrites sur les listes électorales, 525 ont affirmé ne pas vouloir aller voter lors du premier tour des élections régionales 2010.
- Déterminez, à partir de cette enquête, l'intervalle de confiance à $95\%$ de la proportion d'abstentions lors de ce premier tour. Écrivez ses bornes avec quatre décimales.
- Après ce premier tour, le ministère de l'intérieur a annoncé le résultat définitif de l'abstention : $53,64\%$. Un sondage est qualifié de "bon" si l'intervalle de confiance obtenu à partir de celui-ci contient la valeur qu'il est censé estimer. Le sondage de l'énoncé est-il "bon"?
- Un institut a réalisé, avant le premier tour des élections, un "bon" sondage sur un échantillon de 1000 personnes. Donnez un encadrement du nombre de personnes sondées ayant répondu NON à la question : "Irez-vous voter aux élections régionales 2010"?
La carte rectangulaire autour du lac d'Annecy ci-dessous correspond à une zone géographique mesurant 20km de long ( axe Nord-Sud) sur 15 km de large ( axe Est-Ouest)
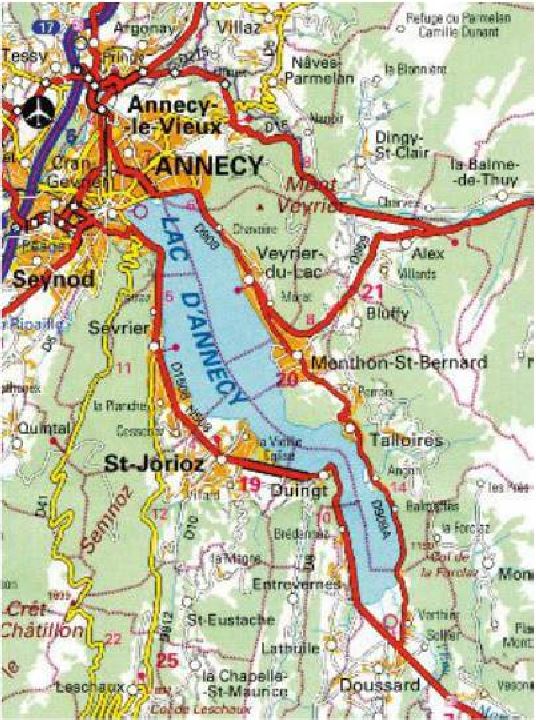
Le but de cet exercice est de déterminez un encadrement de la superficie de ce lac. Pour cela,500 points sont tracés de manière aléatoire sur cette carte. On en dénombre alors 51 qui sont "dans le lac".
On note $p$ la quotient de la superficie du lac par celle de la zone rectangulaire.
-
- A partir de l'expérience relatée dans l'énoncé, déterminez une intervalle de confiance de p au niveau $95\%$. Ecrivez ses bornes avec trois décimales.
- Déduisez-en un encadrement de la superficie du lac ( en $km^2$ ) au niveau de confiance de $95\%$.
- Reprenez la question précédente en utilisant comme intervalle de confiance de p à $95\%$ : $$[f_{obs}-1,96\frac{\sqrt{f_{obs}(1-f_{obs})}}{\sqrt{n}};f_{obs}+1,96\frac{\sqrt{f_{obs}(1-f_{obs})}}{\sqrt{n}}].$$
- Quel est l'intervalle de confiance qui a permis d'obtenir l'estimation la plus précise de la superficie du lac d'Annecy?
- A partir de combien de points tracés aléatoirement sur cette carte peut-on obtenir, à l'aide du premier intervalle de confiance, un encadrement de la superficie du lac d'Annecy d'amplitude inférieure ou égale à 1 $km^2$?
Un sondeur cherche à obtenir, auprès de jeunes scolarisés de 15-16 ans, des réponses sincères à une question sur un sujet sensible, à laquelle on répond par "oui" ou par "non".
Pour éviter les fausses réponses concernant ce sujet sensible, il demande à chaque jeune sondé de tirer au hasard une carte dans un jeu de 32 cartes et de la remettre dans le paquet afin d'être la seule personne à connaitre la carte tirée. Si cette carte est un cœur, alors le jeune doit répondre sincèrement à la question, sinon il doit mentir.
On suppose que les personnes sondées jouent parfaitement le jeu. On note p la proportion de jeunes scolarisé de 15-16 ans qui devraient répondre "oui" et q la porportion de jeunes scolarisés de 15-16 ans répondant "oui" à ce sondage.
- Prouvez, éventuellement à l'aide d'un arbre pondéré, que $q=-0,5p+0,75$.
-
- Sur un échantillon aléatoire de 2500 jeunes scolarisés de 15-16 ans, il y a eu 1375 "oui" à ce sondage. Déterminez un intervalle de confiance de $q$ au niveau $95\%$.
- Déduisez-en un intervalle de confiance de $p$ au niveau de $95\%$.
- Supposons que le sondeur adopte le procédé suivant : si la carte tirée est rouge, alors le jeune doit répondre sincèrement à la question, sinon il doit mentir.Quel problème rencontrerait-il?
Au moment de corriger une question du bac, où il fallait choisir une réponse parmi 4 propositions, un professeur s'exaspère " on dirait qu'ils ont répondu au hasard à cette question !". En fait , sur son échantillon de 120 copies, il a observé 42 bonnes réponses à cette question. Cet échantillon aléatoire est assimilé à une suite de tirage au hasard et avec remise.
On fait l'hypothèse que la proportion de bonnes réponses à cette question est $p=0,25$.
-
- Vérifiez que les trois conditions d'application de la règle de prise de décision sont remplies.
- Déterminez les intervalles de fluctuation (centrés en p) à $95\%$ et à $99\%$ de la fréquence F de bonnes réponses à cette question sur un échantillon aléatoire de taille 120. Ecrivez les bornes de ces intervalles avec trois décimales.
- Pouvez-vous affirmer qu'au seuil de risque de $5\%$, les résultats observés sur l'échantillon confirment l'hypothèse de l'énoncé? Même question mais au seuil de $1\%$.
Dans une usine, une machine produit des barres de métal de longueur 92,50 cm. La machine se déréglant au cours du temps, on veut tester la moyenne des longueurs des barres produites.
On suppose que la variable aléatoire X, qui a tout échantillon de 30 arbres de métal prélevées au hasard associe la moyenne des longueurs, en cm, des barres de l'échantillon , sui t une loi $\mathcal{N}(m;0,03^2)$.
On fait l'hypothèse que la moyenne m des longueurs des barre est encore de 92,50 cm.
- Déterminez, à l'aide de votre calculatrice, un intervalle I centrée en 92,5 tel que $P(X\in I)=0,95$. Ecrivez les bornes de I avec trois décimales.
- Le prélèvement, au hasard, d'un échantillon de 30 barres dans la production de la machine donne les résultats suivants :
Calculez, à $10^{-3}$ près , la moyenne observée $m_{obs}$ des longueurs des 30 barres de métal de cet échantillon.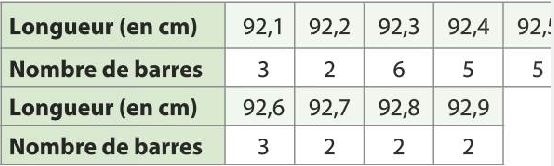
- On définit la règle de prise de décision suivante :
- si $m_{obs}\in I$, alors on accepte l'hypothèse de l'énoncé;
- si $m_{obs}\notin I$, alors on refuse l'hypothèse de l'énoncé au seuil de $5\%$.
Au vu des résultats de cet échantillon, accepte-t-on l'hypothèse de l'énoncé au seuil de risque de $5\%$.

Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.