Considérons la fonction f constante égale à 2 définie sur $\mathbb{R}$, que vaut $\int_{-2}^{3}f(t) dt=$?

Considérons la fonction $f $constante égale à $-2$ définie sur $\mathbb{R}$, que vaut $\int_{-2}^{3}f(t) dt=$

On donne la figure géogébra suivante

Que vaut $\int_{-2}^{3}f(x) dx$?

Les fonctions suivantes sont des primitives de quelle fonction?

• $x\longmapsto x$
• $x\longmapsto \frac{x^2}2$

Déterminer une primitve de chaque fonction :

1. $f:x\longmapsto x^3+3x^2-2x+3$
2. $f:x\longmapsto (2x+3)(x^2+3x)^6$
3. $f:x\longmapsto \frac{2x+3}{x^2+3x}^6$
4. $f:x\longmapsto \sqrt{x+1}$
5. $f:x\longmapsto \frac{x}{x^2+1}$
6. $f:x\longmapsto (2x-1)e^{x^2-x}$
7. $f:x\longmapsto\frac{x}{\sqrt{x^2+1}}$
8. $f:x\longmapsto 2\cos(2x+\pi)$
9. $f:x\longmapsto x^2\sin(x^3)$

Déterminer $\int_{-\pi}^{\pi} -5sin^3(x) dx$.

Quelle est l'aire, en unité d'aire, de la surface délimitée par les courbes représentative de la fonction $x\longmapsto x^2$, de la fonction $x\longmapsto x^3$ et les droites d'équation $x=-1$ et $x=2$?

Vérifiez que la fonction F est une primitive de la fonction $f$ sur l'intervalle I.

1. $F(x)=x\ln(x)-x$; $f(x)=\ln(x)$; $I=]0;+\infty[$
2. $F(x)=(x+1)e^{-x}$; $f(x)=-xe^{-x}$; $I=\mathbb{R}$
3. $F(x)=\frac25 x^2\sqrt{x}$; $f(x)=x\sqrt{x}$; $I=]0;+\infty[$

Déterminez l'expression d'une primitive de la fonction continue $f$ sur l'intervalle indiqué.

1. $f(x)=8x^3-6x^2+1$, $I=\mathbb{R}$.
2. $f(x)=9x^2-4x+5$, $I=\mathbb{R}$.
3. $f(x)=\frac12 x^4-\frac35 x^2+\frac1{10}$, $I=\mathbb{R}$.
4. $f(x)=\frac{10x^4-8x^3+3x^2}{12}$, $I=\mathbb{R}$.
5. $f(x)=\frac2{x^3}$, $I=]0;+\infty[$.
6. $f(x)=-\frac3{x^2}$, $I=]-\infty;0[$.
7. $f(x)=\frac1{2x}$, $I=]0;+\infty[.$.
8. $f(x)=\frac1{2x-1}$, $I=]\frac12;+\infty[$.
9. $f(x)=\frac1{2x-1}$, $I=]-\infty;\frac12[$.
10. $f(x)=-\frac1{x^3}+\frac4{x^2}-\frac1{x}$, $I=]0;+\infty[$.
11. $f(x)=(2x+1)^{2014}$, $I=\mathbb{R}$.
12. $f(x)=x(1-x^2)^5$, $I=\mathbb{R}$.
13. $f(x)=\cos(x)\sin(x)$, $I=\mathbb{R}$.
14. $f(x)=e^x(1-e^x)^2$, $I=\mathbb{R}$.
15. $f(x)=\frac{1}{(2x-1)^{2014}}$, $I=]\frac12;+\infty[$.
16. $f(x)=\frac1{x(\ln(x))^2}$, $I=]1;+\infty[$.
17. $f(x)=\frac{e^x}{(1+e^x)^4}$, $I=\mathbb{R}$
18. $f(x)=\frac1{\sqrt{x-1}}$, $I=]1;+\infty[$.
19. $f(x)=\frac{x}{\sqrt{x^2-1}}$, $I=]1;+\infty[$.
20. $f(x)=\frac{e^x}{2\sqrt{e^x+1}}$, $I=\mathbb{R}$.
21. $f(x)=e^{-2x+1}$, $I=\mathbb{R}$.
22. $f(x)=xe^{-x^2+1}$, $I=\mathbb{R}$.
23. $f(x)=(x+1)e^{x^2+2x+3}$, $I=\mathbb{R}$.
24. $f(x)=\cos(x)e^{\sin(x)}$, $I=\mathbb{R}$.
25. $f(x)=\frac{x-2}{-x^2+4x-3}$, $I=]1;3[$.
26. $f(x)=\frac{e^x}{e^x+1}$, $I=\mathbb{R}$.
27. $f(x)=\cos(2x-\frac{\pi}4)$, $I=\mathbb{R}$.
28. $f(x)=2\sin(\frac{x}2+\frac{\pi}3)$, $I=\mathbb{R}$.

Calculez la valeur exacte de chaque intégrale à l'aide d'une primitive.

1. $I=\int_{-1}^{4}(2x-3)^2 dx$
2. $I=\int_{-2}^{1} (x-4)^3 dx$
3. $I=\int_{0}^{1} (2x+1)(x^2+x) dx$
4. $I=\int_{1}^{2} 2x(x^2+1)^3 dx$
5. $I=\int_{0}^{2} \frac{3t}{(t^2+1)^2} dt$
6. $I=\int_{1}^{2} \frac{t^3}{t^4+1}dt$
7. $I=\int_{0}^{3} \frac{1}{(2t+1)^2}dt$
8. $I=\int_{1}^{2} \frac1{3t+2} dt$
9. $I=\int_{0}^{3} \frac{1}{\sqrt{1+x}} dx$
10. $I=\int_{0}^{-1} \frac2{\sqrt{1-3x}} dx$
11. $I=\int_{-1}^{\sqrt{3}} \frac{3x}{\sqrt{x^2+1}} dx$
12. $I=\int_{\sqrt{2}}^{\sqrt{3}} \frac{x}{\sqrt{x^2-1}} dx$
13. $I=\int_{ln(2)}^{ln(3)} 4e^{t} dt$
14. $I=\int_{0}^{1} te^{t^2-1} dt$
15. $I=\int_{\frac13}^{1} e^{1-2t}dt$
16. $I=\int_{-\frac{\pi}{3}}^{0} \sin(t)e^{\cos(t)} dt$
17. $I=\int_{1}^{2} \frac{x+1}{x^2+2x}dx$
18. $I=\int_{\frac{\pi}6}^{\pi} \frac{\sin(t)-t\cos(t)}{t^2} dt$
19. $I=\int_{0}^{\frac{\pi}{2}} \cos(2t-\frac{\pi}3) dt$
20. $I=\int_{0}^{\frac{\pi}3} \cos(t)-t\sin(t) dt$

1. Déterminez deux nombres a et b telq que pour tout $x\in\mathbb{R}\backslash\{-3;3\}$ : $$\frac{6}{x^2-9}=\frac{a}{x-3}+\frac{b}{x+3}.$$
2. Déduisez-en $J=\int_{4}^{11} \frac{1}{x^2-9} dx$

1. Déterminez les trois nombres réels a, b et c tels que pour tout $x\ne-2$ : $$\frac{x^2-5}{x+2}=ax+b+\frac{c}{x+2}$$
2. Déduisez-en $J=\int_{-1}^{6} \frac{x^2-5}{x+2} dx$

Calculez , dans chaque cas, en utilisant les propriétés de l'intégrale :

1. $I=\int_{1}^{e} \ln(t) dt+\int_{1}^{e} (t+\ln(\frac{1}{t})) dt$
2. $I=\int_{1}^{e}\ln(1+t^2) dt+\int_{0}^{1}\ln(1+t^2) dt-\int_{0}^{e}\ln(1+t^2) dt$

$f$ est la fonction définie sue $\mathbb{R}$ par : $$f(x)=x\sin(x).$$

1. Prouvez que pour tout nombre $x$ : $$f''(x)+f(x)=2\cos(x).$$
2. Déduisez-en la valeur de l'intégrale $I=\int_{0}^{\frac{\pi}2} x\sin(x)$

$f$ est la fonction définie sur $\mathbb{R}$ par $$f(x)=(1-x)e^{x}.$$

1. Prouvez que pour tout nombre réel $x$ : $$f''(x)-2f'(x)+f(x)=0.$$
2. Déduisez-en la valeur de l'intégrale : $$I=\int_{0}^{1} f(t) dt$$

Démontrez les encadrements suivants :

1. $\frac15\leq \int_{1}^{3} \frac{1}{1+x^2} dx \leq 1.$
2. $\frac1{\sqrt{5}}\leq \int_{0}^{\frac12} \frac{1}{\sqrt{1+x^2}} dx \leq \frac12.$
3. $\frac{\sqrt{\ln(2)}}{2}\leq \int_{-\sqrt{\ln(2)}}^{0} e^{-x^2} dx \leq \sqrt{\ln(2)}.$

Calculez la valeur moyenne de la fonction $f$ sur l'intervalle I indiqué.

1. $f(x)=5\sin(2x)$; $I=[0;\pi]$.
2. $5\cos(2x+\frac{\pi}3)$; $I=[0;\frac{\pi}2]$

Pour tout entier naturel $n$ non nul, on pose : $$I_n=\int_{0}^{\frac{\pi}4} x^n\sin(2x) dx.$$

1. Démontrez que pour tout entier naturel $n$ non nul : $$0\leq I_n \leq (\frac{\pi}4)^{n+1}.$$
2. Quelle est la limite de la suite $(I_n)$.

Les courbes d'équations $y=\sqrt{x}$ et $y=x^5$ déterminent, à l'intérieur du carré unité, trois domaines $\mathcal{D}_1$ , $\mathcal{D}_2$ et $\mathcal{D}_3$.

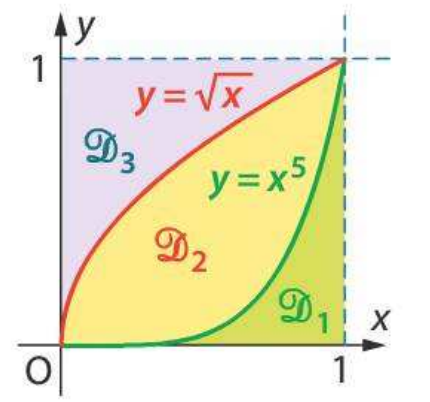
Calculez , en unité d'aire, l'aire de chacun d'eux.

On considère la fonction $f$ définie sur $[0;1]$ par : $$f(x)=\frac{e^x-1}{e^x-x}.$$ $\mathcal{C}$ désigne sa courbe représentative dans un repère orthonormé ( unité graphique : 10 cm). $\Delta$ est la droite d'équation $y=x$.

1. 1. Prouvez que pour tout $x\in[0;1]$ , $$f(x)-x=\frac{(1-x)(e^x-x-1)}{e^x-x}.$$
   2. Etudiez la position relative de $\mathcal{C}$ et $\Delta$ sur $[0;1]$.On admettra que $e^x-x-1$ et $e^x-x$ sont des nombres positifs sur $[0;1]$.
2. Calculez l'aire, en $cm^2$, du domaine plan délimité par la courbe $\mathcal{C}$, la droite $\Delta$ et les droites d'équations $x=0$ et $x=1$.

BAC

$f$ est la fonction définie sur$\mathbb{R}$ par : $$f(x)=\frac{e^x}{1+e^{x}}.$$ $\mathcal{C}$ désigne sa courbe représentative dans un repère orthonormé $(O;\vec{i},\vec{j})$.

1. Prouvez que $\mathcal{C}$ admet deux asymptotes horizontales dont vous préciserez les équations.
2. $\lambda$ désigne un nombre positif. On note $V(\lambda)$ l'intégrale $\int_{-\lambda}^{0} \pi[f(x)]^2 dx.$ On admet que $V(\lambda)$ est une mesure, exprimé en unité de volume , du volume engendrée par la rotation, autour de l'axe des abscisses , de l'arc $\mathcal{C}$ obtenu pour $-\lambda\leq x\leq 0$.
1. Déterminez deux nombres a et b tels que pour tout $x$ : $$\frac{e^{2x}}{(e^x+1)^2}=\frac{ae^{x}}{e^x+1}+\frac{be^x}{(e^x+1)^2}.$$
2. Exprimez $V(\lambda)$ en fonction de $\lambda$.
3. Calculez la limite de $V(\lambda)$ lorsque $\lambda$ tend vers $+\infty$. Interprétez géométriquement ce résultat.

Un cycliste roule sur une route descendante rectiligne et très longue. On note $v(t)$ sa vitesse à l'instant $t$, où $t$ est exprimé en secondes et $v(t)$ en $m.s^{-1}$.

On suppose , de plus que la fonction $v$ ainsi définie est dérivable sur l'intervalle $[0;+\infty[$.

Un modèle simple permet de considérer que la fonction $v$ doit vérifier les conditions : $$v(0)=0 \textrm{ et } 10v'(t)+v(t)=30.$$

1. Prouvez que la fonction $v$ définie sur $[0;+\infty[$ par $v(t)=30(1-e^{-\frac{t}{10}})$ vérifie les conditions indiquées.
2. Etudiez le sens de variation de la fonction $v$ en précisant sa limite en $+\infty$.
3. On considère, dans cette situation, que la vitesse du cycliste est stabilisé lorsque son accélération $v'(t)$ est inférieur à $0,1 m.s^{-2}$. Déterminez, à 1 s près, la plus petite valeur de $t$ à partir de laquelle la vitesse du cycliste est stabilisée.

4. Pour $t\geq 0 $, On admet que la distance parcourue à partir de l'instant initial est $d(t)=\int_{0}^{t}v(u) du$

   Quelle est , à 1 m près , la distance parcourue par ce cycliste en 35 secondes?

Correction de l'exercice 22

BAC

On considère la fonction $f$ définie sur l'intervalle $I=]1;+\infty[$ par $f(x)=\ln(x)+1-\frac{1}{x}.$

1. 1. Etudiez les variations de $f$ sur l'intervalle I.
   2. Déduisez-en le signe de $f(x)$ lorsque $x$ décrit I.
   3. 1. Vérifiez que la fonction $F$ définie sur $]0;+\infty[$ par $F(x)=(x-1)\ln(x)$ est une primitive de $f$ sur $I$.
      2. Justifiez que $F$ est strictement croissante sur $[1;+\infty[$.
      3. Prouvez que l'équation $F(x)=1-e^{-1}$ admet une unique solution, notée $\alpha$, dans l'intervalle $[1;+\infty[$. Donnez un encadrement de $\alpha$ d'amplitude $10^{-2}$.

2. On considère les fonction $g$ et $h$ définies sur $]0;+\infty[$ par $g(x)=\frac{1}{x}$ et $h(x)= \ln(x)+1$. Sur le graphique , on a tracé les courbes $\mathcal{C}_g$ et $\mathcal{C}_h$.

   
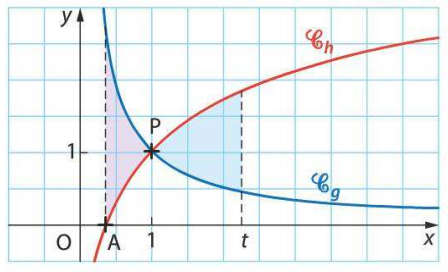
   1. A est le point d'intersection de l'axe des abscisses et de $\mathcal{C}_h$. Quelles sont les coordonnées de A?
   2. P est le point d'intersection des courbes $\mathcal{C}_g$ et $\mathcal{C}_h$. Justifiez que les coordonnées de P sont $(1;1)$.
   3. On note $\mathcal{A}$ l'aire du domaine délimité par $\mathcal{C}_g$, $\mathcal{C}_h$ et les droties d'équations $x=e^{-1}$ et $x=1$.
   4. 1. Exprimez en unité d'aire, l'aire $\mathcal{A}$ à l'aide de la fonction $f$ définie dans la partie A.
      2. Prouvez que $\mathcal{A}=1-e^{-1}$.

   5. $t$ est un nombre strictement supérieur à 1. On note $\mathcal{A}_t$ l'aire du domaine délimité par les droites d'équations $x=1$, $x=t$, et les courbes$\mathcal{C}_g$ et $\mathcal{C}_h$. On veut déterminer une valeur de $t$ telle que $\mathcal{A}=\mathcal{A}_t$.

      1. Prouvez que $\mathcal{A}_t=(t-1)\ln(t)$.
      2. Conclure.

BAC

1. On donne le tableau de variation d'une fonction $f$ dérivable sur $\mathbb{R}$.

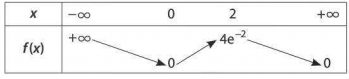
   On définit la fonction $F$ sur $\mathbb{R}$ par $F(x)=\int_{2}^{x} f(t) dt$.

   1. Déterminez les variations de la fonction $F$ sur $\mathbb{R}$.
   2. Prouvez que $0<F(3)<4e^{-2}$.

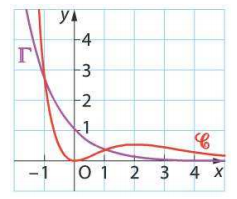
2. On a tracé les représentations graphiques $\mathcal{C}$ et $\Gamma$ des fonctions $f$ et $g$ définies sur $\mathbb{R}$ par : $$f(x)=x^2e^{-x} \textrm{ et } g(x)=e^{-x}.$$

   
   1. 1. Vérifiez que les variations de $f$ ,sont celles du tableau de la partie A.
      2. Etudiez la positions relatives de $\mathcal{C}$ et $\Gamma$.
   2. $h$ est la fonction définie sur $\mathbb{R}$ par $h(x)=(x^2-1)e^{-x}$.
      1. Déterminez une primitive $H$ de $h$ sur $\mathbb{R}$ sachant qu'elle s'exprime sous la forme $H(x)=(x^2+bx+c)e^{-x}$ où a, b, et c sont trois réels.
      2. $\alpha$ est un nombre tel que $\alpha >1$. On considère la partie du plan délimitée par $\mathcal{C}$, $Gamma$ et les droites d'équations $x=1$ et $x=\alpha$. Déterminez en fonction de $\alpha$ l'aire $\mathcal{a}(\alpha)$, exprimée en unité d'aire, de cette partie du plan.
      3. Quelle est la limite de $\mathcal{a}(\alpha)$ lorsque $\alpha$ tend vers $+\infty$?

BAC

Le but de cet exercice est de donner un encadrement du nombre J défini par : $$J=\int_{0}^{1}\frac{x^2e^{x}}{1+x}dx.$$ $f$ est la fonction définie sur $[0;1]$ par : $$f(x)=\frac{e^{x}}{1+x}.$$

1. Etudiez les variations de $f$ sur $[0;1]$.
2. On pose pour tout entier naturel $n$, $S_n=\sum_{k=0}^{n}f(\frac{k}5).$
   1. Justifiez que pour tout entier $k$ entre 0 et 4, on a : $$\frac15f(\frac{k}5)\leq \int_{\frac{k}5}^{\frac{k+1}5} \frac{e^x}{1+x} dx \leq \frac15f(\frac{k+1}5).$$
   2. Déduisez-en l'encadrement suivant : $$\frac15S_4\leq \int_{0}^{1}\frac{e^{x}}{1+x}dx \leq \frac15(S_5-1).$$
   3. Donnez une valeur approchée à $10^{-4}$ près de $S_4$ et de $S_5$, puis déduisez-en l'encadrement :$$1,091\leq \int_{0}^{1}\frac{e^{x}}{1+x}dx \leq 1,164.$$
3. 1. Démontrez que pour tout $x$ de $[0;1]$ : $$\frac{1}{1+x}=1-x+\frac{x^2}{1+x}.$$
   2. Justifiez l'égalité $$\int_{0}^{1}\frac{e^{x}}{1+x} dx=\int_{0}^{1} (1-x)e^{x}dx +J.$$
   3. Calculez $\int_{0}^{1}(1-x)e^{x} dx.$
   4. Déduisez-en un encadrement de J d'amplitude inférieure à $10^{-1}$.