Demander le programme !
- les cas de FI
- les cas d'asymptotes
- la détermination de limite en l'infini
- la déterminantion de limtie en un nombre
Limite d'une fonction à l'infini
Limite à l'infini
limite en $+\infty$
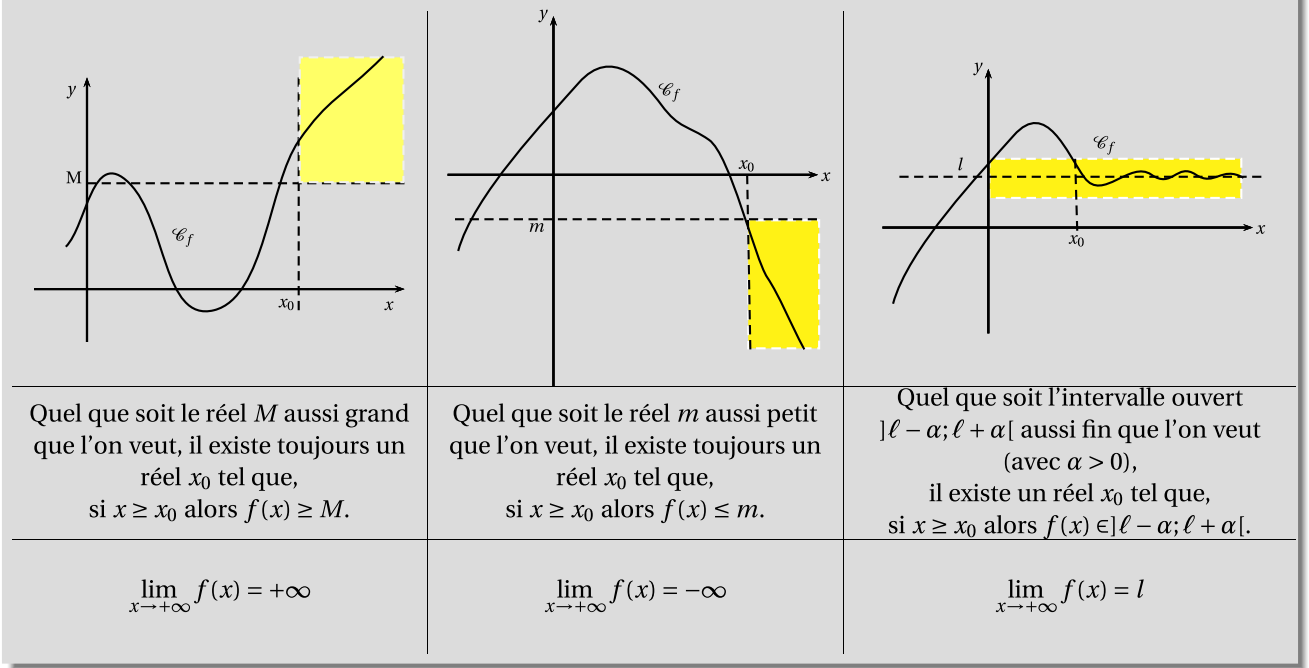
On a des définitions analogues pour décrire le comportement de $f$ au voisinage de $-\infty$ (ou encore, lorsque la variable $x$ tend vers $-\infty$).
limite en $-\infty$
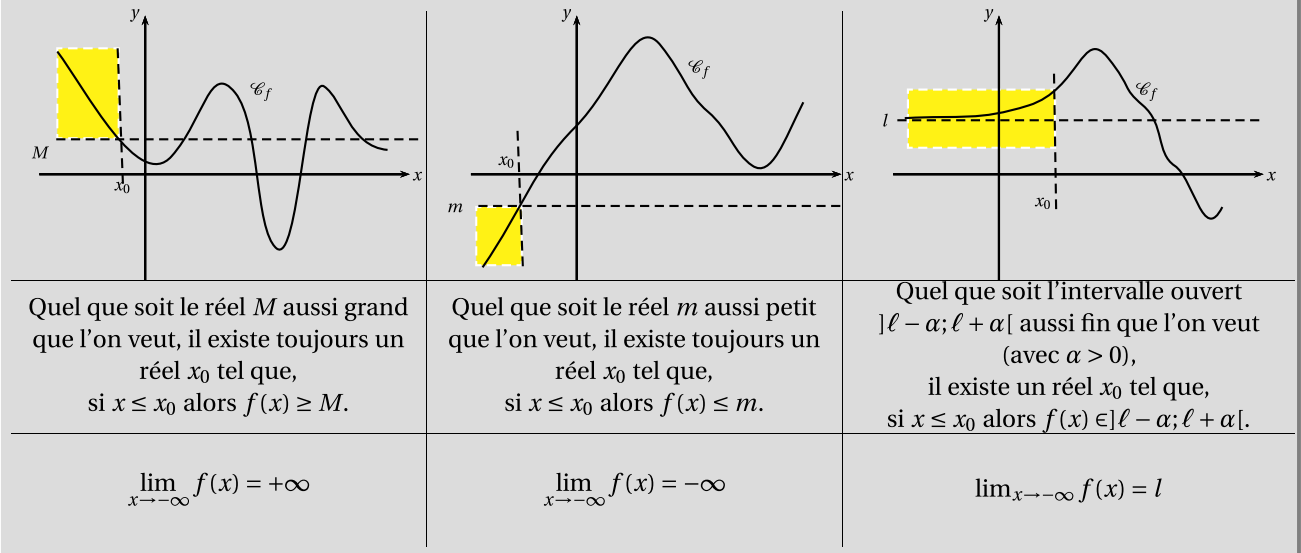
Limites à l'infini de fonctions de références
Soit $n$ un entier naturel non nul fixé.

Asymptotes au voisinage de $+\infty$ ou $-\infty$
Asymptote horizontale
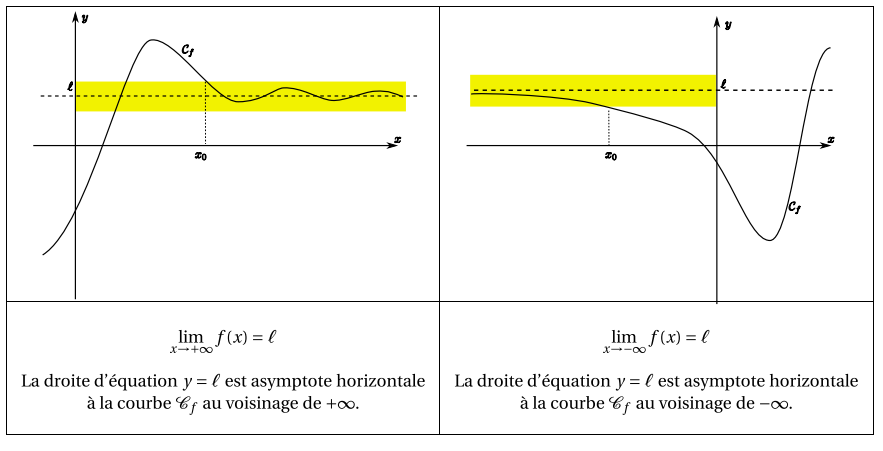
Asymptote oblique

Limite d'une fonction en un point $a$
On considère une fonction $f$ définie sur un intervalle ou une réunion d'intervalles disjoints. On étudiera le problème de la limite d'une fonction en un point $a$ lorsque $a$ appartient à cette réunion d'intervalle ou encore si $a$ est une extrémité de cette réunion d'intervalle.
Limite infinie en $a$. Asymptote verticale
Soit $f$ une fonction définie au voisinage d'un point $a$.
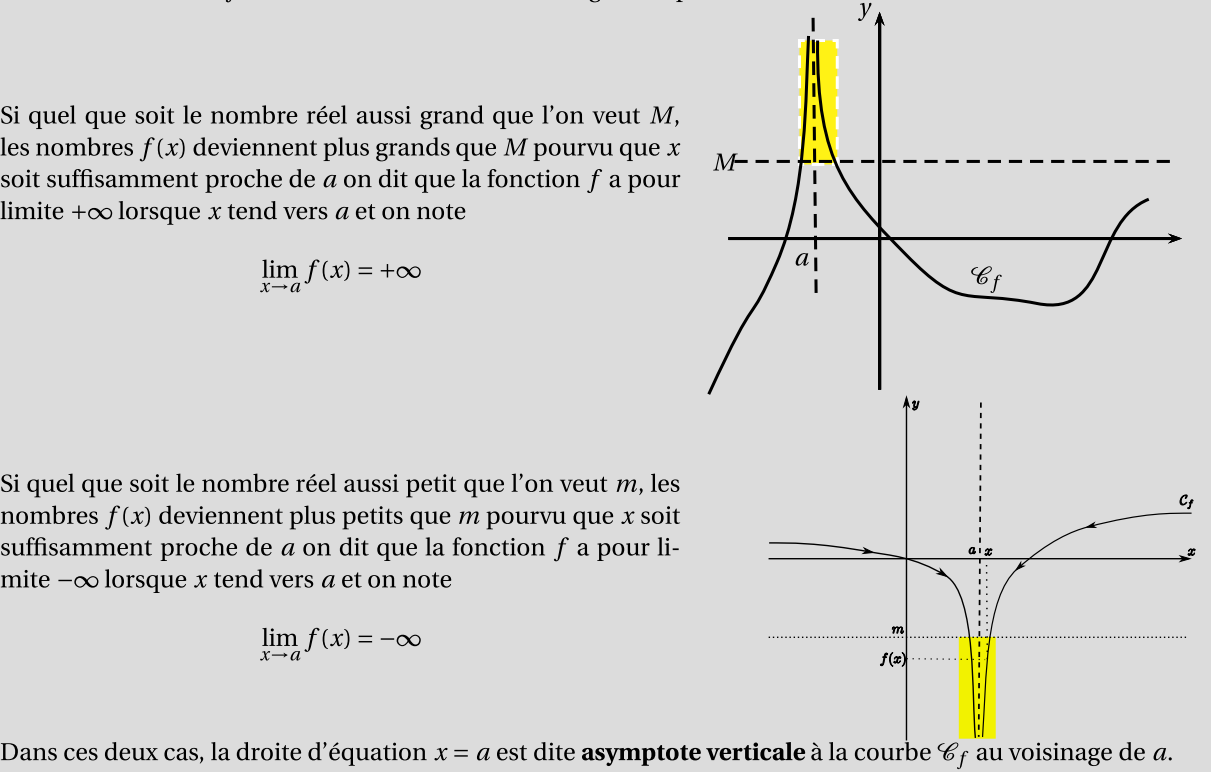
Limite réelle en $a$
Soit $f$ une fonction définie au voisinage d'un point $a$.

Limites des fonctions usuelles.
Soit $a$ un nombre réel.
- si $a\geq 0$,$\lim_{x\to a} \sqrt{x}=\sqrt{a}$
- si $P$ est un polynôme $\lim_{x\to a} P(x)=P(a)$
- si $F$ est une fonction rationnelle avec $a\in \mathcal{D}_F$, $\lim_{x\to a} F(x)=F(a)$
- Plus généralement, si $f$ est une fonction usuelle étudiée en Seconde ou en 1èreS et $a$ est un réel du domaine de définition $\mathcal{D}_f$ de $f$, alors $\lim_{x\to a} f(x)=f(a).$
- Enfin, si $f$ s'écrit comme une somme, différence, produit, quotient ou composée de fonctions usuelles et si $a \in \mathcal{D}_f$, alors $\lim_{x\to a} f(x)=f(a).$
Limite à droite, limite à gauche.
limite à gauche de $a$
On appelle limite à gauche de $a$ la limite de $f$ quand $x$ tend vers $a$ pour des valeur inférieure à $a$.
On note cette limite $\lim\limits_{x\to a^{-}}f(x)$
limite à droite de $a$
On appelle limite à droite de $a$ la limite de $f$ quand $x$ tend vers $a$ pour des valeur supérieure à $a$.
On note cette limite $\lim\limits_{x\to a^{+}}f(x)$
Opérations sur les limites
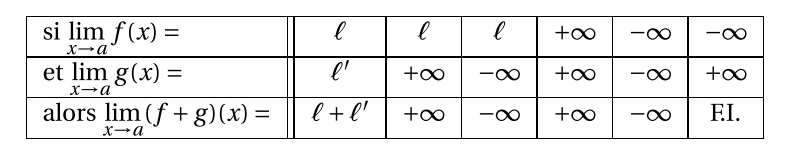
Somme
Produit par un réel $k$ NON NUL
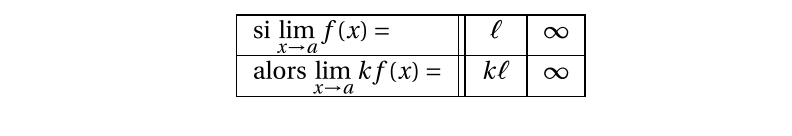
Produit
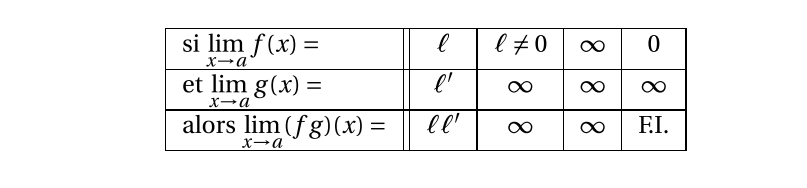
Inverse
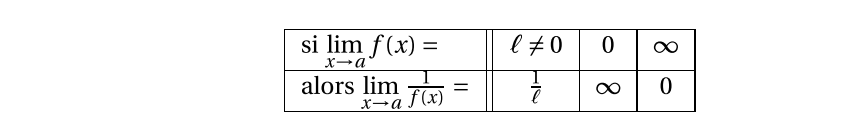
Quotient
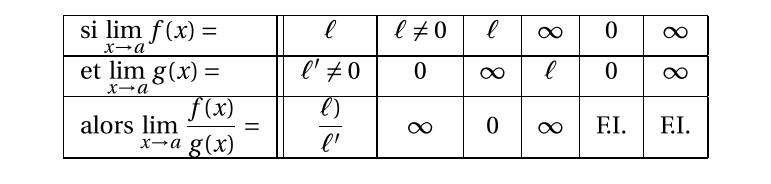
Limite d'une fonction composée
$f$ et $g$ sont des fonctions.
$a$, $b$ et $c$ désignent soit des nombres , soit $+\infty$, soit $-\infty$.
Si $\lim\limits_{x\to a} f(x)=b$ et $\lim\limits_{x\to b} f(x)=c$, alors $\lim\limits_{x\to a} g(f(x))=c$.
- Déterminons la limites de $f:x\longmapsto \sqrt{\frac{x+1}{x+2}}$ en $+\infty$.
- Déterminons la limites de $f:x\longmapsto \sqrt{\frac{x+1}{x+2}}$ en $-2^{-}$
Calcul de limites
Cas des fonctions polynômes au voisinage de l'infini
Déterminer la limite en $+\infty$ et en $-\infty$ de : $g(x)=2x^2+4x+1$; $ h(x)=-3x^4-x$; et $f(x)=10^{-3}x^3-10^{6}-10x.$
Cas des fonctions rationnelles au voisinage de l'infini
Déterminer la limite en $+\infty$ et en $-\infty$ de : $g(x)=\frac{3x^2-1}{x^2+4} $ et $f(x)=\frac{2x-1}{x^2-1}.$
Limite en $a$ d'un quotient $\frac{N}{D}$ tel que $N(a)\neq 0$ et $D(a)=0$
Etudier les limites de la fonction $$f : x\mapsto \frac{-x+3}{(x-1)^2}$$ aux bornes de son domaine de définition.
Etudier les limites de la fonction $$g : x\mapsto \frac{-2x^2+1}{x^2-9}$$ aux bornes de son domaine de définition.
Etudier les limites de la fonction $$h : x \mapsto \frac{x^2}{x-3}$$ aux bornes de son domaine de définition. On interprétera les résultats en terme d'asymptotes.
Quelques méthodes pour lever les indéterminations $\frac{0}{0}$
Etudier les limites de la fonction $$f: x \mapsto \frac{5x^2-3x-2}{x-1}.$$
Indication. --- pour l'étude de la limite en $1$, on pourra factoriser le numérateur.
A chaque tir, un archer atteint sa cible avec une probabilité égale à 0,7.
Combien de tirs doit-il effectuer pour que, avec une probabilité supérieure ou égale à 0,99, il atteigne la cible au moins deux fois ? Au moins trois fois ?
Etudier les limites de la fonction $$g : x \mapsto \frac{\sqrt{x}-3}{x-9}.$$
Indication. --- pour l'étude de la limite en $+\infty$, on pourra mettre le facteur <
Même exercice avec la fonction $$h : x \mapsto \frac{2x}{\sqrt{x+9}-3}.$$
Exercices
limites de fonction et courbe représentative
Par convention, la représentation graphique d'une fonction donne avec exactitude l'allure des "branches infinies" de la courbe. Ainsi, on peut lire les limites d'une fonction sur sa courbe représentative.
Ceci n'est évidement pas vrai lorsqu'on observe la courbe représentative d'une fonction à l'aide de l'outil numérique.
-
Ceci n'est évidement pas vrai lorsqu'on observe la courbe représentative d'une fonction à l'aide de l'outil numérique.
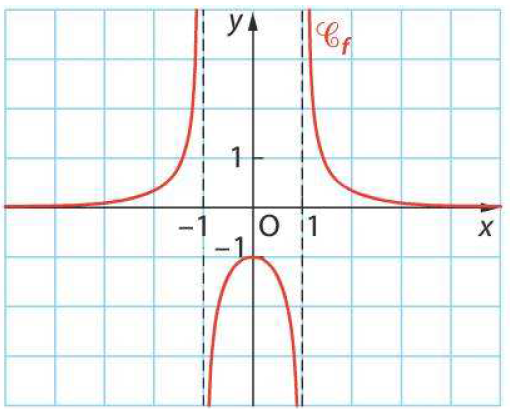
Donnez la limite de $f$ en $-\infty$, en $-1^{-}$, en $-1^{+}$, en $1^{-}$, en $1^{+}$,et en $+\infty$.
-
La courbe $\mathcal{C}_f$ ci-dessous est la représentation graphique d'une fonction $f$ définie sur $\R\backslash\{-2;2\}$.
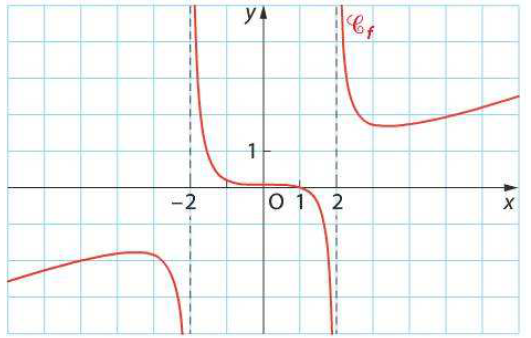
Donnez la limite de $f$ en $-\infty$, en $-2^{-}$, en $-2^{+}$, en $2^{-1}$, en $2^{+}$,et en $+\infty$.
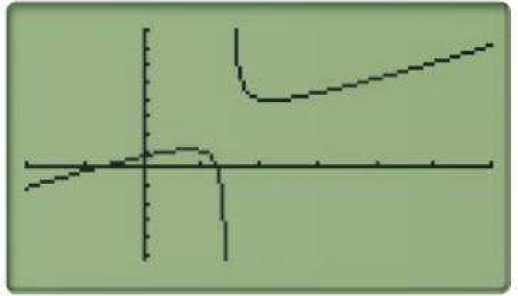
L'écran de calculatrice ci-dessous affiche une partie de la courbe représentative d'une fonction $f$.
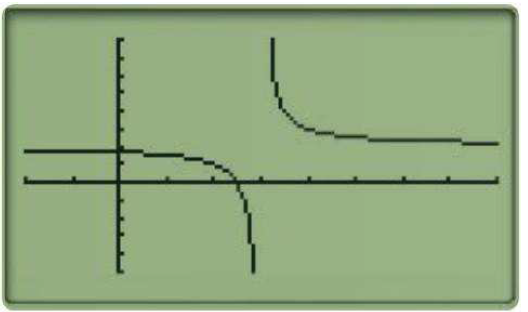
Quelles conjectures pouvez-vous émettre concernant des asymptotes éventuelles?
Que pouvez-vous conjecturer concernant une éventuelle limite en 3 de la fonction $f$ dont l'écran ci-dessous donne une partie de la table de valeurs?

Le tableau ci-dessous décrit les variations d'une fonction $f$ définie sur $]-\infty;2[\cup]2;+\infty[$.
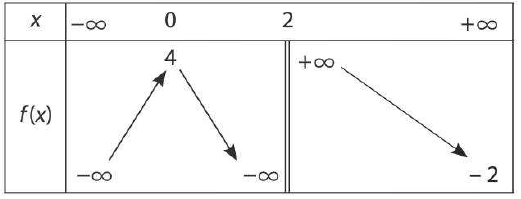
- Précisez la limite en $-\infty$, en $2^{-}$, en $2^{+}$ et en $+\infty$, puis donnez les équations des éventuelles asymptotes horizontales ou verticales à la courbe représentative de $f$.
- Construisez une courbe correspondant au tableau.
Opérations sur limites : fonctions polynomiales et fonctions rationnelles
Dans chacun des cas, étudiez la limite de la fonction $f$ en $+\infty$ et en $-\infty$ et interprétez graphiquement quand c'est possible.
- $f(x)=5x^3+8x-2$
- $f(x)=(x^2-1)(x^3+2)$
- $f(x)=\frac{3}{2x-10}$
- $f(x)=x+\frac1{x-1}$
- $f(x)=\frac{x}{x-1}-\frac{x^2}{x+1}$
Déterminez dans chaque cas la limite et interprétez graphiquement quand c'est possible :
- $\lim\limits_{x\to +\infty} \frac{2x^2+3}{x-2}$
- $\lim\limits_{x\to -\infty} \frac{2x^2+3}{x-2}$
- $\lim\limits_{x\to 2} \frac{2x^2+3}{x-2}$
- $\lim\limits_{x\to +\infty} \frac{1}{x^2}+x$
- $\lim\limits_{x\to -\infty} \frac{1}{x^2}+x$
- $\lim\limits_{x\to 0} \frac{1}{x^2}+x$
$f$ et $g$ sont deux fonctions tells que $\lim\limits_{x\to +\infty}f(x)=+\infty$ et $\lim\limits_{x\to +\infty}g(x)=-\infty$.
Avec ces hypothèses, est-il toujours possible de déterminer les limites suivantes?
- $\lim\limits_{x\to +\infty}f(x)\times g(x)$
- $\lim\limits_{x\to +\infty}2f(x)+g(x)$
- $\lim\limits_{x\to +\infty}2f(x)-g(x)$
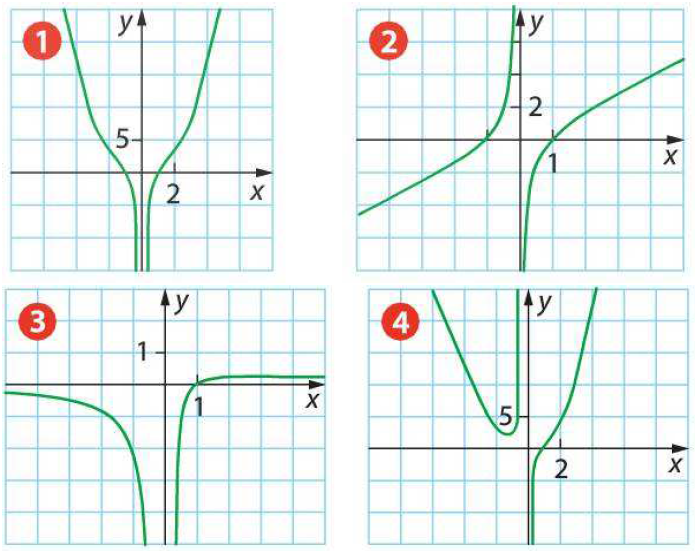
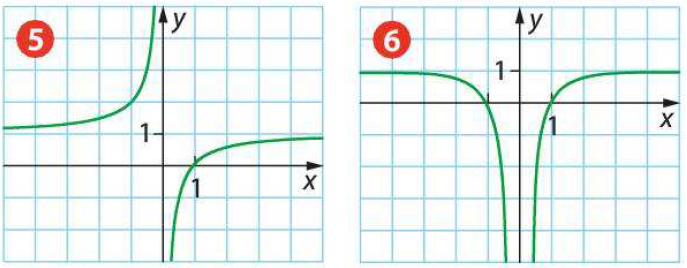
Associez à chacune des fonctions suivantes sa représentation graphique choisie parmi les courbes ci-après.
$f(x)=\frac{x^2-1}{x}$ ; $g(x)=\frac{x^2-1}{x^2}$ ; $h(x)=\frac{x-1}{x^2}$\
$k(x)=\frac{x-1}{x}$ ; $m(x)=x^2-\frac1{x}$ ; $n(x)=x^2-\frac1{x^2}$
La courbe $\mathcal{C}$, représentative d'une fonction, admet pour asymptotes les droites $d_1$, $d_2$ et $\Delta$ tracées ci-dessous, et ces droites seulement.
Pour quelles valeurs de $b$, les fonctions suivantes conviennent-elles?
- $f(x)=\frac{x^2+bx}{x^2-x-2}$
- $g(x)=\frac{2x+b}{(x+1)(x-2)}$
- $h(x)=\frac1{x+1}+\frac{b}{x-2}+1$
Limites de fonctions composées
Dans chacun des cas, étudiez la limite éventuelle de la fonction $f$ en chacun des endroits indiqués.
- $f(x)=\sqrt{x^2+1}$; en $-\infty$ et en $+\infty$.
- $f(x)=\sqrt{x+\frac1{x}}$; en $+\infty$ et en $0$.
- $f(x)=\sqrt{\frac{4x-1}{x+3}}$; en $+\infty$.
- $f(x)=\sqrt{\frac{x^2}{3-2x}}$; en $-\infty$ et en $\frac32$.
- $f(x)=\frac{\sqrt{x}-2}{\sqrt{x+5}-3}$; en 4.
- $f(x)=(x-\sqrt{x}+\frac1{x})^3$; en $+\infty$.
Asymptote oblique
$f$ est la fonction définie sur $\R\backslash\{\frac32\}$ par : $$f(x)=\frac{2x^2-x-2}{2x-3}.$$ La vue d'écran ci-dessous est une fenêtre sur la représentation graphique de $\mathcal{C}_f$ de $f$.
- Utilisez cette vue d'écran pour conjecturer :
- la limite éventuelle de $f$ en $-\infty$, en $+\infty$ et en $\frac32$;
- une équation de l'asymptote verticale à $\mathcal{C}_f$.
- Vérifiez par le calcul l'exactitude de vos conjectures.
-
- Déterminez $a$,$b$ et $c$ tels que pour tout $x\ne\frac32$, $$f(x)=ax+b+\frac{c}{2x-3}.$$
- Montrer que la droite $D$ d'équation $y=ax+b$ est asymptote oblique à $\mathcal{C}_f$ en $+\infty$ et en $-\infty$.
- Étudiez la position relative de $\mathcal{C}_f$ et de D.
On note $\mathcal{C}$ la courbe représentative de la fonction définie sur $\mathbb{R}\backslash\{-\frac32\}$ par $$f(x)=\frac{x^2-5}{2x+3}.$$
- On note $\mathcal{C}$ la courbe représentative de la fonction définie sur $\mathbb{R}\backslash\{-\frac32\}$ par $$f(x)=\frac{x^2-5}{2x+3}.$$
- Vérifiez qu'il existe trois réels $a$, $b$ et $c$ tels que pour tout $x\ne -\frac32$, $f(x)=ax+b+\frac{c}{2x+3}$.
- Montrez que la droite D d'équation $y=ax+b$ est asymptote à $\mathcal{C}_f$ en $+\infty$ en $-\infty$.
- Étudiez la position relative de $\mathcal{C}_f$ et de D.
Synthèse
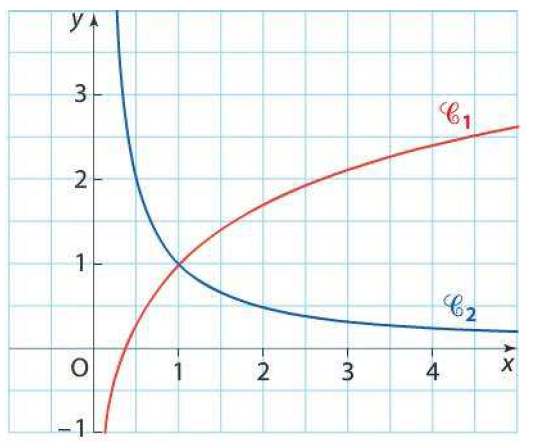
Sur le graphique ci-dessous, on a représenté dans un repère orthonormé les courbes $\mathcal{C}_1$ et $\mathcal{C}_2$ représentatives de deux fonctions $f_1$ et $f_2$ définies sur l'intervalle $]0;+\infty[$.

On sait que :
- l'axe des ordonnées est asymptote aux courbes $\mathcal{C}_1$ et $\mathcal{C}_2$;
- l'axe des abscisses est asymptote à la courbe $\mathcal{C}_2$;
- la fonction $f_1$ est strictement croissante sur $]0+\infty[$;
- la fonction $f_2$ est strictement décroissante sur $]0+\infty[$;
- $\lim\limits_{x \to +\infty}f_1(x)=+\infty$.
$\lim\limits_{x \to +\infty}f_1(x)=+\infty$.
- $\lim\limits_{x\to 0} f_2(x)=$
- 0
- $+\infty$
- On ne peut pas conclure.
- $\lim\limits_{x\to +\infty} f_2(x)=$
- 0
- $0,2$
- On ne peut pas conclure.
-
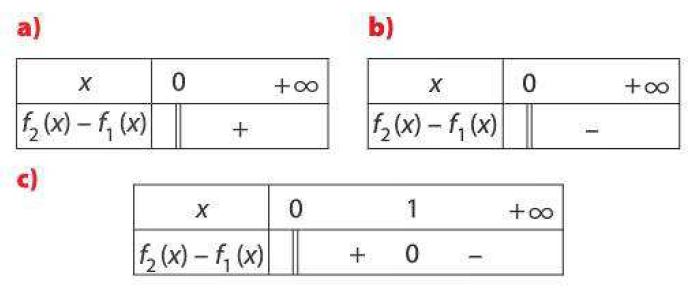
$f$ et $g$ sont deux fonctions définies sur l'intervalle $[1;+\infty[$.
Pour chacune des affirmations ci-dessous, précisez si elle est vraie ou fausse. Justifiez votre réponse.
- Si $\lim\limits_{x\to +\infty}f(x)=+\infty$ et $\lim\limits{x\to +\infty} g(x)=+\infty$, alors $$\lim\limits \frac{f(x)}{g(x)}=1$$
- Si $\lim\limits_{x\to +\infty}f(x)=0$ et $\lim\limits{x\to +\infty} g(x)=0$, alors $$\lim\limits \frac{f(x)}{g(x)}=1$$
- Si pour tout $x\geq 1$, $g(x)-f(x)\leq 0$, et $\lim\limits{x\to +\infty} g(x)=+\infty$, alors $\lim\limits{x\to +\infty} f(x)=+\infty$
- Si $\lim\limits \frac{f(x)}{g(x)}=+\infty$ , alors $\lim\limits_{x\to +\infty}f(x)=+\infty$
- Si $\lim\limits \frac{f(x)}{g(x)}=0$ , alors $\lim\limits_{x\to +\infty}f(x)=0$
- Si $\lim\limits \frac{f(x)}{g(x)}=1$ , alors il existe $a\in[1;+\infty[$ tel que pour tout $x\in[a;+\infty[$, $f(x)=g(x)$.
Etudiez la limite en $+\infty$ de la fonction $f$ définie sur $]0;+\infty[$ par $f(x)=\frac{E(x)}{x}$, où E est la fonction partie entière.

Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.