ln

Définition et propriétés algébriques

Pour tout réel strictement positif $x$, le \textbf{logarithme népérien de x}, noté $\ln x$, est l'unique solution de l'équation $x=e^y$ où $y\in\mathbb{R}$.

La fonction , définie sur $]0;+\infty[$ par $f(x)=\ln x$ est appelée fonction logarithme népérien.

Elle est la fonction réciproque de la fonction exponentielle.

$\ln{1}=0$
$\ln{e}=1$

Déterminer l'ensemble de définition de la fonction $f:x\longmapsto \ln(2x-3)$.

Propriété fondamentale

$$ln(ab)=ln(a)+ln(b)$$

$e^{\ln ab}=ab$ et $e^{\ln a+\ln b}=e^{\ln{a}}\times e^{\ln{b}}=ab$

Ainsi $e^{\ln ab}=e^{\ln a+\ln b}$ ce qui donne $\ln ab=\ln a+\ln b$.

Pour tout réels a et b strictement positifs et tout $n\in\mathbb{Z}$ :

$\ln \frac1{b}=-\ln b$
$\ln \frac{a}{b}=\ln{a}-\ln{b}$
$\ln {a^n}=n\ln a$
$\ln{\sqrt{a}}=\frac12\ln a$

$e^{\ln \frac1{b}}=\frac1{b}$, $e^{-\ln b}=\frac1{e^{\ln b}}=\frac1{b}$. Ainsi $e^{\ln \frac1{b}}=e^{-\ln b}$ ce qui donne $\ln \frac1{b}=-\ln b$
$\ln{\frac{a}{b}}=\ln(a\times \frac1{b})=\ln a + \ln \frac1{b} =\ln a - \ln b$.
Une récurrence permet de montrer le résultat pour $n\in\mathcal{N}$. En remarquant que $\ln{a^{-n}}=\ln\frac1 {a^n}=-\ln{a^n}=-n\ln a$. On obtient la propriété quand l'entier est négatif.
$\ln a=\ln (\sqrt{a}^2)=2\ln a. Ce qui donne \ln{\sqrt{a}}=\frac12 \ln a$.

Exprimer chacun de ces réels en fonction de $\ln 2$, $\ln 3$ et $\ln 5$ : $\ln 24$; $\ln (\frac{64}{75})$; $\ln{\sqrt{3}10^3}$.

Simplifier $\ln(\sqrt{2}-1)+\ln(\sqrt{2}+1)$.

La fonction ln réciproque de la fonction exponentielle

Dans un repère orthonormal, les courbes $(E):y=e^x$ et $(L):y=\ln x$ sont symétriques par rapport à la droite $(\Delta):y=x$.

Limite de la fonction $\ln$

$\lim\limits_{x\to 0}\ln x= -\infty$ et $\lim\limits_{x\to +\infty}\ln x= +\infty$.

Equations et inéquations

Pour tout $x>0$ et $y>0$,

$\ln x=\ln y$ $\Leftrightarrow$ $x=y$
$\ln x<\ln y$ $\Leftrightarrow$ $x<y$
$\ln x<0$ $\Leftrightarrow$ $0<x<1$
$\ln x>0$ $\Leftrightarrow$ $x>1$

Résoudre les équations et les inéquations suivantes :

$\ln x +\ln(x+2)=\ln(1+x)$
$\ln x +\ln(x+2)\leq\ln(1+x)$

Approximation au voisinage de 1

$\lim\limits_{h\to 0} \frac{\ln(1+h)}{h}=1$.

La courbe $C:y=e^x$ admet en $A(0;1)$ une tangente $(T)$, parallèle à $(\Delta):y=x$ et d'équation $y=x+1$.

Soit $s$ la symétrie par rapport à $(\Delta)$, $s(C)=(L):y=\ln x$, $s(A)=A'(1;0)$ et $s(T)=(T')$ est parallèle à $(\Delta)$ donc est de coefficient directeur 1.

En outre, $(T')$ est tangente à $(L)$ au point $A'$ : le nombre dérivé de $\ln $ au point d'abscisse 1 vaut 1.

Ainsi $\lim\limits_{h\to 0} \frac{\ln(1+h)}{h}=1$.

$\lim\limits_{x\to 1} \frac{\ln x}{x-1}=1$

$\lim\limits_{x\to 1} \frac{\ln x}{x-1}=\lim\limits_{h\to 0} \frac{\ln(h+1)}{h}=1$

L'approximation affine de $\ln $ au voisinage de 1 est : $\ln(1+h)=h+h\epsilon(h)$ où $\lim\limits_{h\to 0} \epsilon(h)=0$

La tangente à $\ln$ au point d'abscisse 1 est : $y=\ln'(1)(x-1)+\ln 1=x-1$.

Donc pour $x$ voisin de 1, $\ln x\approx x-1$ ou encore pour $h$ voisin de 0 : $\ln(1+h)\approx h$.

Dérivabilité

$\ln$ est dérivable sur $]0;+\infty[$ et, pour tout $x>0$ $$\ln'(x)=\frac1{x}$$

Soit $a>0$.

$ \lim\limits_{h\to 0} \frac{\ln(a+h)-\ln(a)}h=\lim\limits_{h\to 0} \frac{\ln(\frac{a+h}a)}h=$

$\lim\limits_{h\to 0} \frac{\ln(1+\frac{h}a)}h=$

$\lim\limits_{h\to 0} \frac{\ln(1+\frac{h}a)}{\frac{h}a}\times \frac1a=$

$\frac1a\times \lim\limits_{H\to 0} \frac{\ln(1+H)}H=$

$\frac1a \textrm{ car } ln'(1)=1$

Ainsi pour tout $a>0$, $\ln $ est dérivable en $a$ et $\ln'(a)=\frac1a$.

La formule de dérivation des fonctions composées donne la formule suivante : $$(\ln u)'=\frac{u'}{u}$$

Déterminer l'ensemble de dérivabilité et l'expression de la fonction dérivée de la fonction $f:\longmapsto \ln(x^2-3x-1)$.

Croissances comparées

En l'infini

$$\lim\limits_{x\to +\infty} \frac{\ln x}x=0$$

Montrons d'abord que pour tout $x>0$, $\ln x<x$.

Soit $f:x\mapsto\ln x-x$ définie sur $I=]0;+\infty[$.

$f$ est dérivable sur $I$ et $f'(x)=\frac1x-1=\frac{1-x}x$.

$$\begin{array}{|c|ccccc|} \hline x&0&&1&&+\infty\\ \hline f'(x)&&+&0&-&\\ \hline f&_{-\infty}&\nearrow &^{-1}&\searrow &\\ \hline \end{array}$$ Le maximum de $f$ est atteint quand $x$ vaut 1 et il vaut $-1<0$. Donc pour tout $x>0$, $f(x)<0$ : $\ln x<x$
Montrons que pour tout $x>0$, $\ln x<2\sqrt x$

On sait que pour tout $x>0$, $\ln x<x$ donc $\ln(\sqrt x)<\sqrt x$.

Or $\ln(\sqrt x)=\frac12\ln x$ d'où : $\frac12\ln x<\sqrt x$ i.e. $\ln x<2\sqrt x$

Conclure

Pour tout $x>0$, $\ln x<2\sqrt x \Rightarrow \frac{\ln x}x<2\frac{\sqrt x}x\Rightarrow \frac{\ln x}x<\frac2{\sqrt x}$.

Or si $x>1$, alors $\frac{\ln x}x>0$ d'où pour tout $x>1$ : $0<\frac{\ln x}x<\frac2{\sqrt x}$.

De plus $\lim\limits_{x\to +\infty} \frac2{\sqrt x}=0$ donc d'après le théorème des gendarmes : $$\lim\limits_{x\to +\infty} \frac{\ln x}x=0$$

Déterminer $\lim\limits_{x\to +\infty} \frac{\ln x +2}{x+1}$.

En zéro

Pour tout entier $n$ non nul $\lim\limits_{x\to 0} x\ln(x)=0$

$\lim\limits_{x\to 0} x\ln x=\lim\limits_{x\to 0} \frac1{(\frac1x)}\ln(\frac1{\frac1x}) =\lim\limits_{x\to 0} -\frac1{(\frac1x)}\ln \frac1x=\lim\limits_{y\to +\infty} -\frac1{y}\ln y=\lim\limits_{y\to +\infty} -\frac{\ln y}{y}=0$

Calculer $\lim\limits_{x\to 1} (x-1)\ln(x-1)$.

Fonction logarithme décimal

La fonction logarithme décimal noté $\log$ est la fonction définie sur $]0;+\infty[$ par : $$\log(x)=\frac{\ln x}{\ln(10)}$$

La fonction $\log$ a les mêmes propriétés algébriques que la fonction $\ln$.

Pour tout $n$ entier, $\log(10^n)=\frac{\ln(10^n)}{\ln 10}=\frac{n\ln 10}{\ln 10}=n$ : c'est une raison pour laquelle la fonction $\log$ est très utilisée en physique, chimie et économie.

Exercices

Manipuler les propriétés algébriques de ln

Exprimez en fonction de $\ln(5)$ :

$\ln(125)$
$\ln(\frac{\sqrt{5}}{5})$
$\ln(\frac1{625})$

Simplifiez l'écriture des nombres suivants :

$\ln(3)+\ln(\frac19)$
$3\ln(\sqrt{2})-\frac12\ln(8)$
$\ln(\sqrt{27})+2\ln(2)-\ln(9)-\ln(8)$

Calculez les nombres suivants :

$5-\ln(\frac1{e^2})$
$\ln(e\sqrt{2^3})$
$\ln(\frac{\sqrt{e}}{e^{-2}}$

$f$ est la fonction définie sur $]0;+\infty[$ par : $$f(x)=\ln(e^{\frac1{x}})+e^{-\ln(x)}.$$ Simplifiez l'écriture de $f(x)$.

Résolution d'équation et d'inéquation

Pour quelles valeurs de $x$ peut-on écrire : $$\ln(\frac{1+x}{1-x})=\ln(1+x)-\ln(1-x)?$$
Résolvez dans $]-1;1[$ l'inéquation : $$\ln(\frac{1+x}{1-x})<\ln(1+x).$$
Interprétez graphiquement ce résultat.

$f$ est la fonction définie sur $\mathcal{R}$ par : $$f(x)=\ln(\sqrt{x^2+1}+x)+\ln(\sqrt{x^2+1}-x).$$

Représentez $f$ sur votre calculatrice.
Que conjecturez-vous? Prouvez-le.

$f$ et $g$ sont les fonctions définies sur $]0;+\infty[$ par : $$f(x)=[\ln(x)]^2 \textrm{ et } g(x)=\ln(\frac1{x}).$$

Vérifiez que pour nombre $x>0$, $$f(x)-g(x)=\ln(x)[\ln(x)+1].$$
Résolvez l'inéquation $f(x)-g(x)<0$.
Déduisez-en la position relative des courbes représentatives de $f$ et de $g$.

Résolvez l'équation ou l'inéquation proposée :

$\ln(3-2x)=1$
$\ln(x^2-8)=0$
$\ln(3-x)=-2$
$\ln(1-\frac1{x})=2$
$e^{x+2}=3$
$e^{\frac{x}{x+1}}=2$
$(e^x+1)(e^x-4)=0$
$\ln(e^x+1)=2$
$\ln(2x-1)\geq -1$
$\ln(x-3)<2$
$-1\leq \ln(x) \leq 2$
$\ln(1+e^x)\leq 2$
$e^{x-1}<2$
$(e^x+1)(e^x-4)\leq 0$
$e^{\frac{x+1}{x}}>3$
$\ln(x-2)\leq \ln(2x-1)$
$\ln(x)\leq \ln(x^2-2x)$
$\frac12\ln(2x)=\ln(3-x)-\ln(\sqrt{x+1})$
$\ln(5-x)-\ln(3)+\ln(x-1)\geq 0$
$[ln(x)]^2-2\ln(x)-3=0$
$[ln(x)]^2-2\ln(x)-3\geq 0$
$3e^{2x}-7e^x+2=0$
$3e^{2x}-7e^x+2>0$

Quel est l'ensemble des nombres pour lesquels l'égalité $\ln(\frac{x-1}{x+2})=\ln(x-1)-\ln(x+2)$ est vraie?

Résolvez, dans chaque cas, l'inéquation d'inconnue $n$ un entier naturel.

$(\frac25)^n\leq 0,2$
$(1+\frac3{100})^n\geq 2$

Calculs de limite

Les suites $(u_n)$ et $(v_n)$ sont définies sur $\mathcal{N}^*$ par $u_n=2\ln(n)-n$ et $v_n=e^{u_n}$.

Déterminez la limite de la suite $(u_n)$
Déduisez-en la limite de la suite $(v_n)$

Les suites $(u_n)$ et $(v_n)$ sont définies sur $\mathcal{N}^*$ par $u_n=n^ne^{-n}$ et $v_n=\ln(u_n)$

Déterminez la limite de la suite $(u_n)$
Déduisez-en la limite de la suite $(v_n)$

Etudiez la limite de la fonction $f$ au borne de l'intervalle I.

$f(x)=\frac{1}{\ln(x)}$; $I=]1;+\infty[$
$f(x)=x(1-\ln(x))$; $I=]0;+\infty[$
$f(x)=\ln(\frac{x+1}{x-4})$; $I=]-\infty;-1[$
$f(x)=x+\ln(x+1)-\ln(x)$; $I=]0;+\infty[$
$f(x)=\frac{x-\ln(x)}{x}$; $I=]0;+\infty[$
$f(x)=\frac1{x}+\ln(x)$; $I=]0;+\infty[$
$f(x)=x+\frac{\ln(x)}{x}$; $I=]0;+\infty[$
$f(x)=\ln(2+e^x)$; $I=\mathcal{R}$

Synthèse

$g$ est la fonction définie sur $\mathcal{R}$ pa $g(x)=xe^{x}+1.$ Démontrez que pour $x\in\mathcal{R}$, $g(x)>0$.
$f$ est la fonction définie sur $I=]0;+\infty[$ par : $$f(x)=e^x+\ln(x)$$
1. Démontrez que pour pour tout $x$ de I, $f'(x)=\frac{g(x)}{x}$.
2. Dressez le tableau de variation de $f$.
3. Déduisez-en que pour tout nombre $m$, l'équation $f(x)=m$ a une unique solution.

Bac

Dans un repère orthonormé, on a tracé les courbes $\mathcal{C}$ et $\Gamma$ d'équations respectives : $$y=e^x \textrm{ et } y=\ln(x).$$

On rappelle que pou tout nombre $x$ strictement positif : $$e^x>\ln(x).$$

A tout nombre $x$ strictement positif, on associe le point M de $\mathcal{C}$ et le point $N$ de $\Gamma$ de même abscisse $x$.

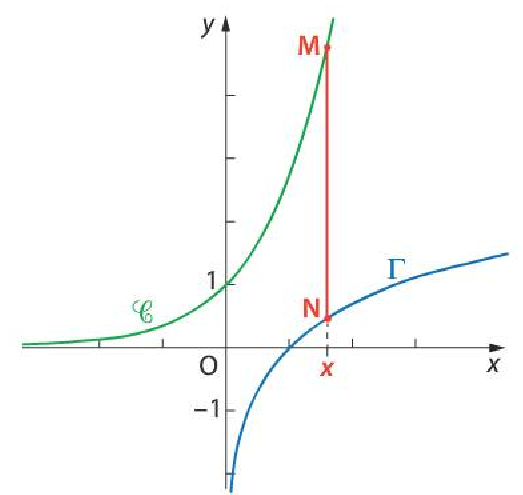
Le but de l'exercice est de trouver la valeur de $x$ pour laquelle la distance MN est minimale.

On note $\phi$ la fonctions définie sur $]0;+\infty[$ par : $$\phi(x)=e^x-\ln(x).$$
1. Calculer $\phi'(x)$ et démontrez que $\phi'(x)=0$ admet, dans $]0;+\infty[$, une unique solution notée $\alpha$.\\ Déterminez une valeur approchée de $\alpha$ à $10^{-2}$ près.
2. Déduisez-en que la distance MN est minimale lorsque $x=\alpha$.
1. Justifiez que $e^{\alpha}=\frac1{\alpha}$.
2. Déduisez-en que les tangentes à $\mathcal{C}$ et $\Gamma$ aux points d'abscisse $\alpha$ sont parallèles.

$f$ est la fonction définie sur $[0;+\infty[$ par : $$f(x)=x^2\ln(x) \textrm{ si } x>0 \textrm{ et } f(0)=0.$$

Démontrez que $f$ est continue et dérivable en 0.
La courbe $\mathcal{C}$ admet un minimum au point A. Quelles sont les coordonnées de A?
Démontrez qu'il existe deux tangentes à $\mathcal{C}$ passant par O. Précisez une équation de chacune des tangentes.

$f$ est la fonction définie sur $\mathcal{D}=]-\infty;-1[\cup]-1;+\infty[$ par $f(x)=x\ln(\frac{x-1}{x+1}).$
On vous propose le raisonnement suivant :
"$f$ est dérivable sur $\mathcal{D}$ comme composée de fonctions dérivables sur $\mathcal{D}$. Pour tout $x$ de $\mathcal{D}$, on peut écrire : $$f(x)=x[\ln(x-1)-\ln(x+1)].$$ On obtient alors : $$f'(x)=\ln(x-1)-\ln(x+1)+x[\frac1{x-1}-\frac1{x+1}],$$ soit $$f'(x)=\ln(\frac{x-1}{x+1})+\frac{2x}{x^2-1}.""$$ Ce raisonnement est-il exact?

Dans un repère orthonormé, les courbes $\mathcal{C}$ et $\Gamma$ représentation respectivement la fonction $f$ définie sur $]0;+\infty[$ par $f(x)=\ln(x)$ et la fonction $g$ définie sur $]-3;+\infty[$ par $g(x)=\ln(2x+6)$.

A et C dont les point de $\mathcal{C}$ d'abscisses respectives 1 et 3.

B et D sont les points de $\Gamma$ d'abscisses respectives -2 et 0.

Dites si les affirmations suivantes sont vraies ou fausses. Justifiez vos réponses.

Les tangentes en A à $\mathcal{C}$ et en B à $\Gamma$ sont parallèles.

Le quadrilatère ABDC est un parallélogramme.

Si M et N sont deux points de $\mathcal{C}$ et $\Gamma$ de même ordonnées, alors la distance MN est constante.

Si I et J sont deux points de $\mathcal{C}$ et $\Gamma$ de même abscisse $x$, alors $\lim\limits_{x\to+\infty} IJ=\ln(2)$.

$f$ et $g$ sont les fonctions définies sur $I=]-\infty;0[$ par : $$f(x)=e^x+\ln(-x) \textrm{ et } g(x)=xe^x+1.$$ Parmi les propositions suivantes, dites celle qui sont exactes. Justifiez votre réponse.

Pour tout $x\in I$, $g'(x)=e^x$
Pour tout $x\in I$, $f'(x)=\frac{g(x)}{x}$
Pour tout $x\in I$, $g(x)>0$
la fonction $f$ est strictement croissante sur I.
$\lim\limits_{x\to -\infty} f(x)=+\infty$
L'équation $f(x)=0$ a une unique solution $\alpha$ dans I et $-1<\alpha<0$.

La suite $(u_n)$ est définie par : $$u_0=3 \textrm{ et pour tout entier naturel n, } u_{n+1}=e\sqrt{u_n}.$$

Démontrez par récurrence que pour tout n de $\mathcal{N}$ : $$u_n>0.$$
On note $(v_n)$ la suite définie sur $\mathcal{N}$ par $v_n=\ln(u_n)-2$.
1. Démontrez que la suite $(v_n)$ est géométrique. Précisez sa raison.
2. Déduisez-en une expression de $(v_n)$ puis $(u_n)$ en fonction de $n$.
1. Quelle est la limite de la suite $(v_n)$?
2. Prouvez que la suite $(u_n)$ converge vers $e^2$.

On note $\mathcal{C}$ la courbe représentative de la fonction $f$ définie sur $]1;+\infty[$ par : $$f(x)=\frac{x}{\ln(x)}.$$

1. Dressez le tableau de variation de $f$.
2. Déduisez-en les coordonnées du point A correspondant au minimum de $f$.
3. Démontrez que pour tout nombre $x>e$, $f(x)>e$.
On définie la suite $(u_n)$ par : $$u_0=a \textrm{ avec } a>e \textrm{ et pour tout } n\in\mathcal{N}, u_{n+1}=f(u_n)$$
1. A l'aide d'une calculatrice, tracez l courbe $\mathcal{C}$ représentative et la droite $\Delta$ d'équation $y=x$. Conjecturez les variations de la suite $(u_n)$ et sa limite éventuelle.
2. Démontrez que la suite u est décroissante.
3. Déduisez-en que la suite $(u_n)$ converge et précisez sa limite $l$.

On rappelle que : Une suite qui tend vers $+\infty$ si, pour tout nombre A, tous les termes de la suites sont supérieurs à A à partir d'un certain rang.

Démonstration
Démontrez qu'une suite croissante non majorée tend vers $+\infty$.
Application
$f$ est la fonction définie sur $]0;+\infty[$ par : $$f(x)=x+\ln(x).$$
1. 1. Etudiez les variations de $f$ et dressez son tableau de variation.
  2. Démontrez que pour tout $n\in \mathcal{N}$, l'équation $f(x)=n$ admet une unique solution $\alpha_n$ dans l'intervalle $]0;+\infty[$. Ainsi $\alpha_n+\ln(\alpha_n)=n$.
2. 1. Placez $\alpha_1$, $\alpha_2$, $alpha_3$ et $\alpha_4$ sur le dessin ci-dessous.
  2. Quelle st la valeur exacte de $\alpha_1$.
  3. Démontrez que la suite ($\alpha_n$) est strictement croissante.
3. 1. Déterminez une équation de la droite $\Delta$ tangente à $\mathcal{C}$ au point d'abscisse 1.
  2. Etudiez la position relative de $\mathcal{C}$ et $\Delta$.
4. 1. Démontrez que pour $n\in\mathcal{N}^*$, $\frac{n+1}{2}\leq \alpha_n$
  2. Déduisez-en la limite de la suite $(\alpha_n)$

On note $\mathcal{C}$ la courbe représentative de la fonction $f$ définie sur $]1;+\infty[$ par : $$f(x)=\ln(x)-\frac1{\ln(x)}.$$

Le but de l'exercice est de chercher les tangentes à $\mathcal{C}$ passant par l'origine O du repère.

1. Soit $a$ un nombre de l'intervalle $]1;+\infty[$. Démontrez que la tangente $T_a$ à $\mathcal{C}$ au point d'abscisse $a$ passe par l'origine si, et seulement si $f(a)-af'(a)=0$
2. On note $g$ la fonction définie sur $]1;+\infty[$ par : $$g(x)=f(x)-xf'(x).$$
1. Démontrez que sur $]1;+\infty[$, les équations $g(x)=0$ et $(\ln(x))^3-(\ln(x))^2-\ln(x)-1=0$ sont équivalentes.
2. Après avoir étudié les variations de la fonction $u$ définie sur $\mathcal{R}$ par $u(t)=t^3-t^2-t-1$, démontrez que la fonctions $u$ s'annule une fois et une seule sur $\mathcal{R}$.
3. Déduisez-en l'existence d'une unique tangente à $\mathcal{C}$ passant par O.

$f$ est la fonction définie sur $]-1;+\infty[$ par : $$f(x)=x=\frac{\ln(x+1)}{x+1}.$$ On note $\mathcal{C}$ la courbe représentative de $f$. $\Delta$ est la droite d'équation $y=x$.

1. Calculez $f'(x)$ pour tout $x\in]-1;+\infty[$
2. Pour tout $x\in]-1;+\infty[$, on pose : $$N(x)=(1+x)^2+\ln(1+x)-1.$$
  1. Vérifiez que l'on définit ainsi une fonctions strictement croissante sur $]-1;+\infty[$.
  2. Calculez $N(0)$ et déduisez-en les variations de $f$.
3. Calculez les coordonnées du point d'intersection de la courbe $\mathcal{C}$ et de la droite $\Delta$.
Etude d'une suite convergente
1. Démontrez que : si $x\in[0;4]$, alors $f(x)\in[0;4]$.
2. On considère la suite $(u_n)$ définie par $u_0=4$ et pour tous $n$ de $\mathcal{N}$, $u_{n+1}=f(u_n)$.
  1. Tracez, à l'aide de la calculatrice, la courbe $\mathcal{C}$ et la droite $\Delta$. Conjecturez les variations de la suite $u$ et son éventuelle limite.
  2. Démontrez que pour tout $n\in\mathcal{N}$, $u_n\in[0;4]$.
  3. Etudiez le sens de variation de la suite $u$.
  4. Démontrez que $u$ converge et déterminer sa limite $l$.

Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.