Demander le programme !

  1. la définition d'une propabilité
  2. les définition d'intersection , d'union , de complémentaire
  3. les formules de premières sur les probabilités
  4. la définition d'une probabilité conditionnelle
  5. la formule des probabilités totales
  6. définir l'indépendance de deux événements
  1. un arbre pondéré
  2. l'interprétation d'un événement en terme de probabilité conditionnelle
  3. la mobilisation de ses savoirs sur les suites pour résoudre un problème de probabilités

Probabilités : rappels

On lance deux dés à 6 faces et on s'interresse à la somme des deux dés.

  1. Quel est l'univers?
  2. Citer une éventualité et un événement qui n'est pas une éventualité.
  3. On note $A=\{9;10;11;12\}$ et $B$= "obtenir une somme inférieure ou égale à 9."
    1. Préciser l'événement $A\cup B$ et $A \cap B$
    2. Préciser $\bar{A}$

Probabilité

Une probabilité sur un ensemble fini $\Omega$ est une application de $\Omega$ dans $[0;1]$ vérifiant l'égalité :

$$\sum_{\omega \in \Omega}p(\omega)=1$$

Reprendre l'exercice précédent et déterminer : $P(A)$, $P(B)$, $P(\bar{B})$, $P(A\cap B)$ et $P(A\cup B)$

Probabilité conditionnelle

Probabilité de A sachant B

Soit $P$ une probabilité sur l'univers $\Omega$, et $A$ un événement tel que $P(A)\neq 0$.

Pour tout événement $B$, on appelle probabilité de $B$ sachant $A$ la probabilité de l'événement $B$ en considérant que l'univers est $A$.

Reprendre l'exercice 1 et déterminer $P_A(B)$ et $P_B(A)$

$$P_A(B)=\dfrac{P(A\cap B)}{P(A)}$$

L'application qui à tout événement B associe le réel $P_A(B)$ définit une probabilité sur $\Omega$, appelée probabilité conditionnelle sachant A.

Grâce à ce théorème vous pouvez appliquer toutes les propriétés du paragraphe précédent aux probabilités conditionnelles.

On lance un dé équilibré à six faces numérotées de 1 à 6.

Soit A l'événement le résultat est pair, on a :

Soit B l'événement le résultat est un multiple de 3, on a :

Formule des probabilités totales

On dit que les ensembles $A_1,A_2,...,A_n$ forment une partition de $\Omega$ quand :

Formule des probabilités totales.

Soit $A_1, A_2, ..., A_n$ $n$ évènements de probabilité non nulle réalisant une partition de l'univers $\Omega$, alors : $$P(B)=P(B\cap A_1)+P(B\cap A_2)+...+P(B\cap A_n)$$ En particulier, si $A$ est un événement de probabilité non nulle de $\Omega$ alors $$P(B)=P(B\cap A)+P(B\cap \bar{A})$$

On utilise en général avec des partitions de deux ou trois éléments pas rarement plus.

Arbre pondéré

Pour décrire une expérience aléatoire comportant des probabilités conditionnelles, il est conseillé de construire un arbre pondéré.

Dans un arbre, chaque branche relie deux noeuds. Sur chaque branche, on note la probabilité correspondante.

Un chemin est une suite de branches. La probabilité d'un chemin s'obtient en multipliant des probabilités de chaque branche.

La somme des probabilités affectées aux branches issues d'un même n\oe ud est 1.

La formule des probabilités totales permet de calculer la probabilité d'un événement B en effectuant la somme des probabilités de tous les chemins menant à B.

Un jeu électronique de statégie propose des parties de deux niveaux différents.

Au lancement d'un nouveau jeu, l'appareil choisit lui-même, à l'exclusion de toute autre possibilité, une partie de niveau 1 (événement $N_1$) avec une probabilité de $\frac23$, et une partie de niveau 2 (événement $N_2$) avec une probabilité $\frac13$.

La probabilité qu'un joueur gagne une partie de niveau 1 est $\frac34$, celle qu'il gagne une partie de niveau 2 est $\frac25$.

Le joueur lance une partie. Quelle est la probabilité qu'il la gagne ?

On s'intéresse au jeu de dé suivant :

On mise 5 euros.

On lance le dé une fois, si le chiffres obtenues est 5 ou 6 on relance le dé sinon on perd sa mise.

Au deuxième lancée on gagne 100 euros sur un 6 sinon on perd.

Modéliser une partie avec un arbre pondéré.

On propose l'algorithme suivant :

1 def jeu():
2   D=randint(1,6)
3   if D<4:
4         G=-5
5   else:
6       D=randint(1,6)
5       if D<5:
6           G=-5
7       else:
8           G=95
9   return G

Modifier l'algorithme pour obtenir la moyenne de gain de 1000 parties.

Proposer un changement de règle pour rendre ce jeu équitable.

Indépendance

Evénements indépendants

Evenement indépendant

Soit $P$ une probabilité sur l'univers $\Omega$.

On dit que les événements A et B sont indépendants si : $$P(A\cap B)=P(A)P(B)$$

Si $P(A)\neq 0$, on a : A et B sont indépendants si et seulement si $P_A(B)=P(B)$

On suppose que $P(A)\neq 0$.

Si A et B sont indépendants alors $P(A\cap B)=P(A)P(B)$ donc $P_A(B)=\dfrac{P(A\cap B)}{P(A)}=P(B)$.

Réciproquement, si $P_A(B)=P(B)$ alors $P(A\cap B)=P_A(B)P(A)=P(B)P(A)$ donc A et B sont indépendants.

Pour le lancer un dé équilibré à six faces, A est l'événement le résultat est pair et B le résultat est 2

$P(A\cap B)=\frac16$ et $P(A)=\frac12$, $P(B)=\frac16$ d'où $P(A)P(B)=\frac1{12}\neq \frac16$.

Ainsi A et B ne sont pas indépendants.

Montrer que si A et B sont indépendants alors A et $\bar{B}$ le sont également. Que dire de $\bar{A}$ et $\bar{B}$.

Variables aléatoires indépendantes

Sur un même univers $\Omega$, on définit les variables aléatoires $x$ prenant les m valeurs $x_1,x_2,...,x_m$ et $Y$ prenant les $k$ valeurs $y_1,y_2,...,y_k$.

On dit que les variables aléatoires $X$ et $Y$ sont indépendantes si pour tout entier $i$ de $\{1,...,m\}$ et pour tout entier $j$ de $\{1,...,k\}$ alors les événements $(X=x_i)$ et $(Y=y_j)$ sont indépendants.

Expériences aléatoires indépendantes

On dit que des expériences aléatoires répétées sont indépendantes si le résultat de l'une d'entre elle n'a aucune influence sur les résultats des autres.

Exercices

Calculer des probabilités conditionnelles

A et B sont deux événements relatifs à une même experience aléatoire tels que : $$P(A)=0,5, P(B)=0,6 \textrm{ et } P(A\cup B)=0,8.$$ Calculer $P(A\cap B)$, $P_{A}(B)$ et $P_{B}(A)$.

A et B sont deux événements relatifs à une même experience aléatoire tels que : $$P(A)=0,4, P_{B}(A)=0,3 \textrm{ et } P(A\cap B)=0,2.$$ Calculer $P_{A}(B)$, $P(B)$ et $P(A\cup B)$.

et B sont deux événements d'un même univers tels que : $$P(A)=\frac13, P_{A}(B)=\frac14 \textrm{ et } P_{\bar{A}}(B)=\frac12.$$ Calculer $P(A\cap B)$, $P(\bar{A}\cap B)$ et $P(B)$.

Deux ateliers A et B fabriquent des puces électroniques. Pour une commande de 2000 pièces, A produit 1200 puces et B le reste. Une étude a montré que A produit $4\%$ de puces défectueuses et que B en produit $3\%$.

On prélève une puce au hasard dans la commande.

On appelle A l'évènement "La puce provient de A", B "la puce provient de B" et D "La puce est défecteuse".

  1. Recopiez puis complétez le tableau des effectifs de la commande.

    $D$ $\bar{D}$ Total
    A
    B
    Total
  2. Calculez sous forme de fraction les probabilités suivantes :
    1. $P(D)$; $P(A\cap B)$; $P(A\cap D)$ ; $P_{D}(A)$
    2. $P(\bar{D})$; $P(\bar{D}\cap B)$ ; $P_{\bar{D}}(A)$

Un lot de bulbes de tulipes est composé de deux variétés :

$60\%$ de la variété A dont $95\%$ donneront une fleur;

$40\%$ de la variété B donc $90\%$ donneront une fleur.

On prend un bulbe au hasard dans ce lot.

On note F l'événement "Le bulbe produit une fleur".

  1. Réalisez un tableau à double entrée qui résume la situation.
  2. Justifiez le calcul de la probabilité de l'événement F.

Dans un club sportif, $30\%$ des membres pratiquent le tennis, $60\%$ sont des hommes et parmi eux, $55\%$ ne jouent pas au tennis.

On interroge au hasard un membre de ce club.

Quelle est la probabilité, si c'est une femme, qu'elle ne pratique pas de tennis?

Utiliser un arbre

  1. Recopiez puis complétez l'arbre pondéré ci-dessous

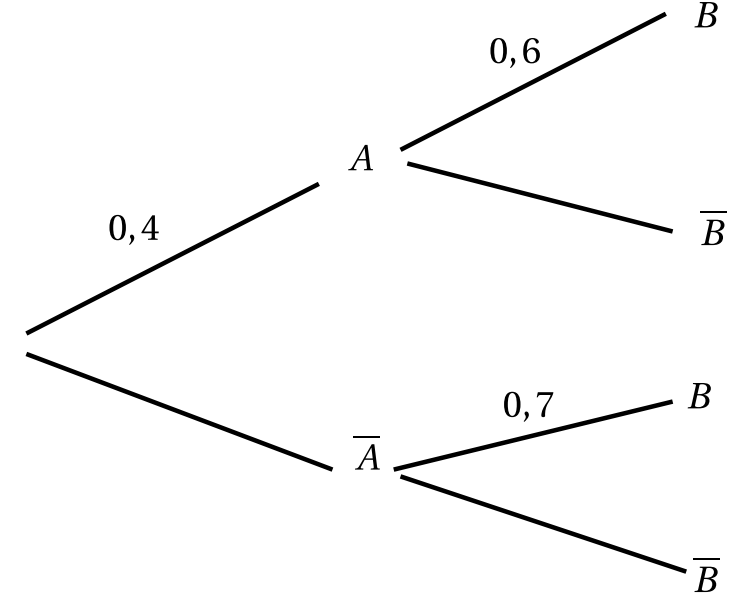
      2. Calculez les probabilités des événements : $A\cap B$; $A\cap \bar{B}$; $\bar{A}\cap B$; $\bar{A}\cap \bar{B}$.

Une urne contient deux boules blanches et trois noires. On tire l'une après l'autre deux boules au hasard et sans remise.

  1. Représentez l'expérience par un arbre
  2. Calculez la probabilité d'obtenir :
    1. deux boules blanches;
    2. deux boules noires;
    3. une boule blanche et une boule noire.

Une école d'ingénieurs organise la sélection de ses futurs étudiants de la manière suivante :

On choisit un candidat au hasard. On considère les événements suivants :

  1. Recopiez puis complétez l'arbre pondéré décrivant différente étapes de la sélection.

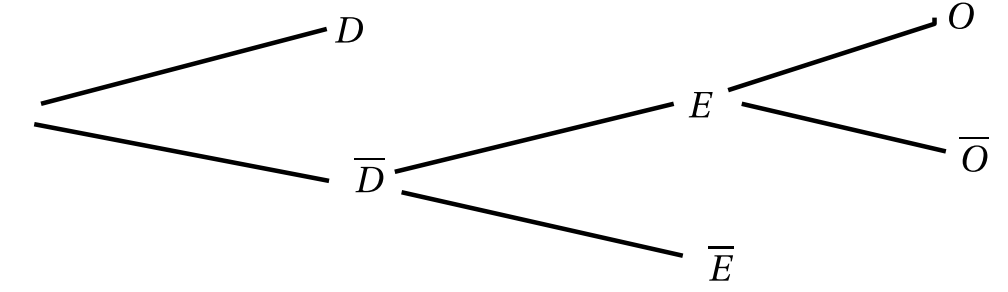
  2. Calculez les probabilités $P(E)$ et $P(O)$.
  3. Justifiez que la probabilité que le candidat soit admis est $P(A)=0,32$.
  4. Parmi les candidats admis, quelle est la proportion de ceux qui ont été admis sur dossier?

Une grande entreprise est divisé en deux secteurs notés A et B.

$65\%$ de ses salariés travaillent dans le secteur A.

Le directeur des ressources humaines s'intéresse au niveau de stress des employés. Un questionnaire informatisé est proposé de manière anonyme à tous les salariés des deux secteurs.

Cette enquête révèle que dans le secteur A, $20\%$ du personnel se dit stressé, tandis que dans le secteur B, ce taux est $30\%$. On choisit au hasard le questionnaire d'un des employés.
On note S l'événement " L'employé est stressé".

    1. Construisez un arbre pondéré représentant l'expérience.

    2. Complétez le tableau ci-contre par les probabilités qui conviennent.

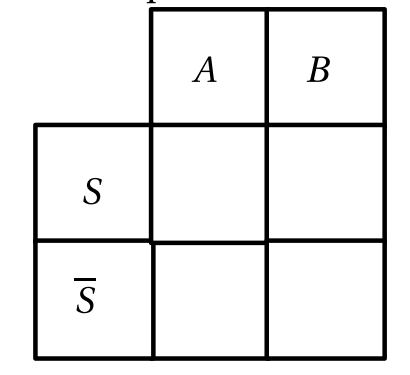
  2. L'entreprise examine l'opportunité d'installer une salle de repos. Le projet ne sera réalisé que si le taux d'employés stressés dépasse $25\%$.

    L'implantation de la salle aura-t-elle lieu ?

A la suite d'un sondage effectué à propos de la construction d'un barrage, on estime que :

$65\%$ de la population concernée est contre la construction, et parmis ces opposants, $70\%$ sont des écologistes.

parmis les personnes qui ne sont pas opposées à la construction, $20\%$ sont des écologistes.

On interroge une personne au hasard.

  1. Calculez la probabilité qu'elle soit opposée à la construction du barrage et écologiste.
  2. Calculez la probabilité qu'elle ne soit pas opposée à la construction du barrage et soit écologiste.
  3. Déduisez-en la probabilité qu'une personne interrogée soit écologiste.

Un bijoutier vend des perles de culture pour fabriquer des colliers. Ces perles n'ont que deux couleurs possibles : argent(A) et noir(N).

D'autre part, elles n'ont que trois formes possibles : sphérique(S), équilibrée (E) ou baroque (B).

Dans son stock, $44\%$ des perles sont équilibrées et $40\%$ sont baroques. De plus, $60\%$ des perles sont argentées et , parmi elles, $15\%$ sont sphériques et la moitié sont baroques.

Le bijoutier choisit une perle au hasard dans son stock.

On se propose de représenté l'expérience par un arbre pondéré du type indiqué, que vous compléterez au fur et à mesure.

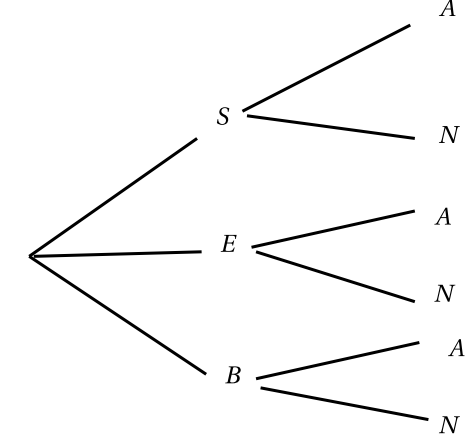
  1. Reproduisez et complétez cet arbre par les probabilités fournies par l'énoncé.
    1. Quelle est la probabilité de $S\cap A$? de $B\cap A$?
    2. Justifiez que : $$P(S\cap A)+P(E\cap A)+P(B\cap A)=P(A).$$ Déduisez-en $P(E\cap A)$.
    3. Calculez, sous forme fractionnaire, $P_{S}(A)$, $P_{E}(A)$, $P_{B}(A)$.
  3. Déduisez-en l'arbre complet.

L'indépendance

Une association propose différentes activités à ses 96 adhérents, dont l'aviron et le badminton.

Douze membres s'inscrivent pour l'aviron, trente-deux pour le badminton dont quatre pour les deux. On prend au hasard la fiche d'un adhérent.

On considère les événements:

  1. Les événements A et B sont-ils indépendants?
  2. En est-il de même pour $\bar{A}$ et $\bar{B}$?

A et B sont deux événements relatifs à une expérience aléatoire représentée par l'arbre suivant.

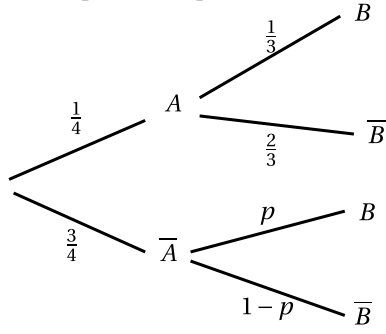
Comment choisir la valeur de, p pour que les événements A et B soient indépendants?

Une urne contient cinq boules blanches et cinq boules noires. On en prélève $n$ ($n\geq 2$) au hasard, successivement et avec remise.

    1. Calculez les probabilités des événements : "Toutes les boules tirées sont de la même couleur"; "On obtient exactement une boule blanche".
    2. On considère les événements :
      • A: "On obtient des boules des deux couleurs";
      • B: "On obtient au plus une boule blanche".

      Déduisez-en les probabilités suivantes : $$P(A\cap B)=\frac{n}{2^n}, P(A)=1-\frac1{2^{n-1}}, P(B)=\frac{n+1}{2^n}$$

  2. Prouvez que A et B sont indépendants si, et seulement si, $2^{n-1}=n+1$.
  3. On considère la suite $(u_n)$ définie pour tout entier $n\geq 2$ par $u_n=2^{n-1}-(n+1)$.
    1. Calculez $u_2$, $u_3$, $u_4$.
    2. Prouvez que la suite $(u_n)$ est strictement croissante.
  4. Déduisez-en la valeur de l'entier naturel $n$ pour que les événements A et B soient indépendants.

Synthèse

En France, les statistiques font apparaître que parmi les adultes, environ $4\%$ des hommes et $5\%$ des femmes sont asthmatiques. Dans la population, on considère l'ensemble des couples homme-femme.

Dans cet exercice, les résultats seront arrondis, si nécessaire, à $10^{-3}$ près.

  1. Etude de l'état d'asthme du couple

    On choisit un couple au hasard. On note H l'événement " l'homme est asthmatique" et F "La femme est asthmatique".

    On admet que les événements F et H sont indépendants.

    1. Recopiez puis complétez le tableau de probabilités ci-contre.

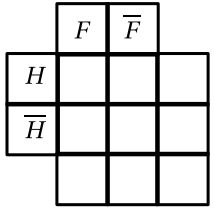
    2. Déduisez-en la probabilité de chacun des événements suivants concernant les deux adultes du couple :

        A: "Aucun n'est asthmatique";

        B: "Un seul est asthmatique";

        C: "Les deux sont asthmatiques".

  2. Transmission de l'asthme au premier enfant

    Les études actuelles montrent que :

    • si aucun des parents n'est asthmatique, la probabilité que leur enfant soit asthmatique est $0,1$;
    • si un seul des deux parents est asthmatique, la probabilité que leur enfant soit asthmatique est $0,3$;
    • si les deux parents sont asthmatiques, la probilité que leur enfant soit asthmatique est $0,5$.

    On note E l'événement "le premier enfant du couple est asthmatique".

    1. Construisez un arbre illustrant cette situation.
    2. Calculez $P(E)$.
    3. Calculez les probabilités conditionnelles $P_{E}(A)$ et $P_{E}(\bar{A})$. Interprétez ces deux résultats.
    4. Quelle est la probabilité qu'un enfant non asthmatique ait au moins l'un de ses deux parents asthmatique?

BAC

Avant le début des travaux de construction d'une autoroute, une équipe d'archéologie préventive procède à des sondages successifs en des points régulièrement espacés sur le terrain.

Si la $n$-ième sondage donne lieu à la découverte de vestiges, il est dit positif.

On désigne par $V_n$ l'événement "Le $n$-ième sondage est positif" et on note $p_n$ sa probabilité.

L'expérience acquise au cours de ce type d'investigation permet de prévoir que :

On suppose que le premier sondage est positif c'est à dire que $p_1=1$.

  1. Calculez les probabilités des événements suivants :
    • A: "Les deuxième et troisième sondages sont positifs";
    • B: "Les deuxième et troisième sondages sont négatifs".
  2. Calculez la probabilités $p_3$ que le troisième sondage soit positif.
  3. On désigne par $n$ un entier naturel tel que $n\geq 2$.

Recopiez puis complétez l'arbre ci-dessous en fonction des données de l'énoncé.

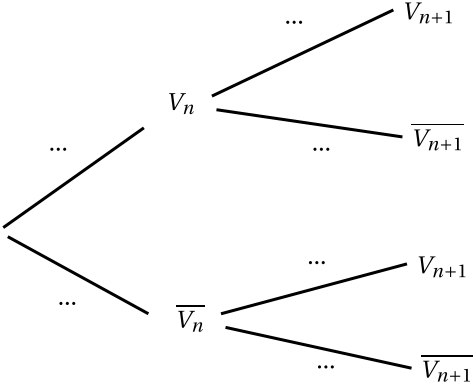
  1. Prouvez que pour tout entier $n\geq 1$, $$p_{n+1}=0,5p_n+0,1.$$
  2. On note $u$ la suite définie pour tout entier $n\geq 1$ par : $$u_n=p_n-0,2.$$
    1. Démontrez que $u$ est une suite géométrique dont vous préciserez le premier terme et la raison.
    2. Exprimez $p_n$ en fonction $n$.
    3. Calculez et interprétez la limite de la suite $(p_n)$.

BAC

Laura débute un jeu dans lequel elle a autant de chance de gagner que de perdre la première partie.

On admet que si elle gagne une partie, la probabilité qu'elle gagne la suivante est $0,6$; si elle perd une partie, la probabilité qu'elle perde la suivante est $0,7$.

Pour tout entier $n\geq 1$, on note $G_n$ l'événement "Laura gagne la $n$-ième partie".

  1. Calculez les probabilités $P(G_2)$ et $P(\bar{G_2})$.
  2. Pour tout entier $n\geq 1$, on pose : $$x_n=P(G_n) \textrm{ et } y_n=P(\bar{G_n}).$$ Prouvez que pour tout entier $n\geq 1$ :$$x_{n+1}=0,6x_n+0,3y_n \textrm{ et } y_{n+1}=0,4x_n+0,7y_n.$$
  3. Pour tout entier $n\geq 1$, on pose : $$v_n=x_n+y_n \textrm{ et } w_n=4x_n-3y_n.$$
    1. Prouvez que la suite $v$ est constante.
    2. Démontrez que la suite $(w_n)$ est géométrique puis exprimez $w_n$ en fonction de $n$.
    1. Pour tout entier $n\geq 1$, exprimez $x_n$ en fonction de $n$.
    2. Prouvez que la suite $(x_n)$ converge vers un nombre que vous préciserez. Interprétez ce résultat.

BAC

Les résultats seront donnés sous forme de décimale en arrondissant à $10^{-4}$ près.

Dans un pays, $2\%$ de la population est contaminé par un virus.

A.On dispose d'un test de dépistage de ce vorus qui a les propriétés suivantes :

On fait passer ce test à une personne choisie au hasard dans cette population.

On note V l'événement " la personne est contaminée par le virus" et T l'événement "Le test est positif".

  1. Traduisez la situation à l'aide d'un arbre pondéré.
  2. Démontrez que la probabilité que le test soit positif est $0,0492$.
    1. Justifiez par le calcul la phrase suivante : " Si le test est positif, il y a environ $40\%$ de chances que la personne soit contaminée".
    2. Déterminez la probabilité qu'une personne ne soit pas contaminée sachant que son test est négatif.

B. On choisi successivement et au hasard dis personnes de la population.

On considère que les choix sont indépendants.

On note X la variable aléatoire qui donne le nombre de personnes contaminées parmi ces dix personnes.

  1. Justifiez que X suit une loi binomiale dont vous rpéciserez les paramètres.
  2. Calculez la probabilité qu'il y ait au moins deux personnes contaminées parmi les dix.

BAC

Dans un zoo, l'unique activité d'un manchot est l'utilisation d'un bassin aquatique équipé d'un sautoir pour plonger et d'un toboggan.

On a observé si un manchot choisit :

Lors du premier passage, les deux équipements ont la même probabilité d'être choisis.

Pour tout entier $n\geq 1$, on considère les événements :

$S_n$: " le manchot utilise le sautoir lors de son $n$-ième passage";

$T_n$: " Le manchot utilise le toboggan lors de son $n$-ième passage".

Pour tout entier $n\geq 1$, on pose $u_n=P(T_n)$.

    1. Vérifiez que $P(T_2)=0,25$

    2. Recopiez puis complétez l'arbre ci-dessous.

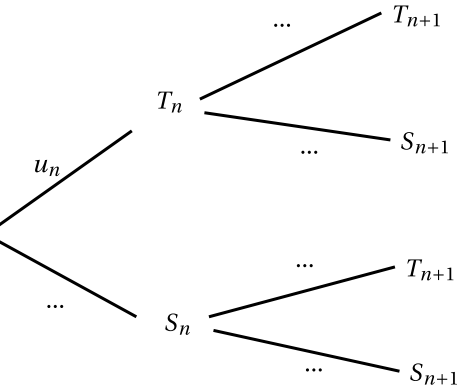
    3. Démontrez que pour tout entier $n\geq 1$ : $$u_{n+1}=0,1 u_n+0,2.$$
    4. à l'aide d'une calculatrice, indiquez une conjecture concernant la limite de la suite $(u_n)$.
  2. On considère la suite $(v_n)$ définie pour tout entier $n\geq 1$ par $v_n=u_n-\frac29$
    1. Prouvez que la suite $(v_n)$ est géométrique. Précisez sa raison et son premier terme.
    2. Exprimez $v_n$ puis $u_n$ en fonction de $n$.
    3. Calculez la limite de la suite $(u_n)$. Ce résultat permet-il de valider la conjecture précédente?
Licence Creative Commons
Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.