Lois de probabilité à densité

Loi de probabilité sur un intervalle-densité

Soit $I=[a;b]$ un intervalle borné de $\mathbb{R}$, avec $a<b$ et $f$ une fonction continue positive sur I, telle que $\int_{a}^{b} f(t) dt=1$.

On définit une loi de probabilité sur l'intervalle I d'un variable aléatoire X, en associant à tout intervalle $[c;d]$ inclus dans I, le nombre : $$P(X\in[c;d])=\int_{c}^{d}f(t) dt.$$ On dit que $f$ est la densité de cette loi de probabilité sur $I$.

Un entrepôt accueille tous les matins des camions de livraison sur un créneau de deux heures d'ouverture, de 7h30 à 9h30. On intéresse à l'heure d'arrivée d'un camion qui se présente tous les matins à l'entrepôt aux heures d'ouvertures.

On définit ainsi une variable aléatoire sur $[7,5; 9,5]$.

On suppose que sa densité est la fonction $f:x\longmapsto |x-8,5|$.

  1. Vérifier que $f$ est bien une densité
  2. Déterminer la probabilité que le camion arrive entre 8h12 et 8h36.
  3. Déterminer la probabilité que le camion arrive à 8h00.
Correction de l'exemple 1

Une remarque en passant :

Loi uniforme sur $[a;b]$.

Densité de loi uniforme

Une loi est uniforme sur $[a;b]$ si sa loi de probabilité est de densité constante : $$f:x\longmapsto \frac1{b-a}.$$

Si X est une variable aléatoire X suit une loi uniforme sur $[a;b]$ on :

  1. $P(X\in[c;d])=\frac{d-c}{b-a}$
  2. L'espérance de X est $E(X)=\int_{a}^{b} t\times \frac1{b-a} dt =\frac{a+b}2$

On considère une variable X qui suit la loi uniforme sur $[-2;8]$.

  1. Donner la densité de cette loi.
  2. Déterminer $P(X\in[0;1])$.
  3. Donner l'espérance de $X$.
Correction de l'exemple 2

loi exponentielle

densité de la loi exponentielle

La loi exponentielle de paramètre $\lambda$ est la loi de probabilité sur $[0;+\infty[$ de densité : $$f:x\longmapsto \lambda e^{-\lambda x}$$

Si T est une variable aléatoire de loi exponentielle de paramètre $\lambda$ :

  1. Pour tout intervalle $J$ d'extrémités c et d, avec $0\leq c\leq d$: $$P(T\in J)=\int_{c}^{d}\lambda e^{-\lambda t} dt .$$
  2. Pour tout réel $a\geq 0$, $P(T\leq a)=P(T<a)=1-e^{-\lambda a}.$
  3. Pour tout réel $a\geq 0$, $P(T\geq a)=P(T>a)=1-P(T\leq a)=e^{-\lambda a}.$

Soit T une variable aléatoire de loi exponentielle de paramètre 2.

Déterminer $P(T\in[1;2])$ et $P(T>1)$.

Soit $T$ une variable aléatoire suivant la loi exponentielle de paramètre $\lambda$ ($\lambda >0$).

Pour tous réels positifs $t$ et $h$ , $$P_{(T\geq t)}(T\geq t+h)=P(T\geq h)$$

$P_{(T\geq t)}(T\geq t+h)=P(T\geq h)=\frac{P[(T\geq t)\cap (T\geq t+h)]}{P(T\geq t)}=\frac{P(T\geq t+h)}{P(T\geq t)}=\frac{e^{-\lambda(t+h)}}{e^{-\lambda t}}=e^{-\lambda h}=P(T\geq h)$

Cette propriété s'appelle "durée de vie sans vieillissement" car elle montre que T sur un laps de temps $h$ ne dépend pas de l'age $t$ à partir duquel on considère cet événement.

Les lois exponentielles modélisent des phénomènes dont la durée de vie n'est pas affectée par l'âge, comme par exemple celle d'un atome radioactif ou encore le temps d'attente à une file d'attente.

$$E(T)=\lim\limits_{x\to +\infty}\int_{0}^{x}t\times \lambda e^{-\lambda t} dt=\frac1{\lambda}.$$

L'espérance d'une variable aléatoire de loi exponentielle de paramètre $\frac{1}{\pi}$ est $\pi$

Loi normale

Loi normale centrée réduite

Théorème de Moivre-Laplace.

Soit $X_n$ une variable aléatoire qui suit la loi binomiale $B(n;p)$.

On pose $$Z_n=\frac{X_n-np}{\sqrt{np(1-p)}}$$ Pour tous réels a et b , avec $a<b$, on a : $$\lim\limits_{n\to +\infty} P(Z_n\in[a;b])=\int_{a}^{b}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}2} dt .$$

La loi normale centrée réduite $\mathcal{N} (0;1)$ est la loi de densité la fonction $f$ définie sur $\mathbb{R}$ par : $$f(t)=\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}2}.$$

En pratique on considère cette approximation d'une loi binomiale par une loi normale quand les données vérifies les trois conditions suivantes :

  1. $n\geq 30$
  2. $np\geq 5$
  3. $n(1-p)\geq 5$

On définit la fonction $\Phi$ sur $\mathbb{R}$ par $\Phi(x)=P(Z\leq x)$, où $Z$ est une variable aléatoire qu suit une loi normale centrée réduite.

  1. $P(a<Z<b)=\Phi(b)-\Phi(a)$

  2. $\Phi(-a)=1-\Phi(a)$

Si $X$ est une variable aléatoire centrée réduite on a:

$E(X)=\int_{-\infty}^{+\infty}tf(t) dt = \lim\limits_{x\to +\infty}\lim\limits_{y \to +\infty}\int_{x}^{y}tf(t) dt=$

$\lim\limits_{x\to +\infty}\lim\limits_{y \to +\infty}\int_{x}^{y}\frac{t}{\sqrt{2\pi}}e^{-\frac{t^2}2} dt=[-\frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}2}]^{y}_{x}=\lim\limits_{x\to +\infty}\lim\limits_{y \to +\infty}-\frac{1}{\sqrt{2\pi}}(e^{-\frac{y^2}2}-e^{-\frac{x^2}2})=0$

Soit X une variable aléatoire suivant la loi normale centrée réduite $\mathcal{N}(0;1)$. Pour tout réel $\alpha\in]0;1[$, il existe un unique réel positif $u_{\alpha}$ tel que :$$P(-u_{\alpha}\leq X\leq u_{\alpha})=1-\alpha$$

On considère la fonction $g$ définie sur $[0;+\infty[$ par : $$ g(t)=P(-t\leq X\leq t)$$

Comme $f$ est paire, on a , pour tout réel r positif : $g(t)=\int_{-t}^{t} f(x) dx = 2\int_{0}^{t} f(x) dx$

Comme $f$ est continue et positive, on en déduit que $g$ est dérivable, et que sa dérivée $2f$ est strictement positive, donc que $g$ est strictement croissante sur $[0;+\infty[$.

On a de plus : $g(0)=0$ et $\lim_{x\to +\infty} g(t)=1$.

Soit $\alpha\in]0;1[$.

On a : $0<1-\alpha < 1$ , le corollaire du TVI permet de conclure à l'existence et l'unicité du $u_{\alpha}$ du théorème.

Deux valeurs à connaitre !

Déterminer à l'aide de la calculatrice $u_{0,1}$.

Loi Normale $\mathcal{N}(\mu; \sigma^2)$

Soient un réel $\mu$ et un réel strictement positif $\sigma$.

On dit qu'une variable aléatoire X suit une loi normale $\mathcal{N}(\mu; \sigma^2)$ si , $\frac{X-\mu}{\sigma}$ suit la loi normale centrée réduite $\mathcal{N}(0;1)$.

Dans ce cas $E(X)=\mu$ et $V(X)=\sigma^2$.

Soit $X$ une variable aléatoire de loi $\mathcal{N}(-2;100)$.

Déterminer les probabilités suivantes en utilisant directement la calculatrice puis en se ramenant à la loi centrée réduite.

  1. $P(-8\leq X \leq 50)$
  2. $P(X<10)$
  3. $P(X\geq 9)$
  4. $P(X\leq -8)$

Soit X une variable aléatoire de loi normale $\mathcal{N}(\mu; \sigma^2)$ :

  1. $P(X\in[\mu-\sigma;\mu+\sigma])=0,683$ à $10^{-3}$ près.
  2. $P(X\in[\mu-2\sigma;\mu+2\sigma])=0,954$ à $10^{-3}$ près.
  3. $P(X\in[\mu-3\sigma;\mu+3\sigma])=0,997$ à $10^{-3}$ près.

Exercices

Loi à densité

On considère la fonction $f$ définie sur $[0;1]$ par : $$f(x)=3x^2.$$

  1. Justifiez que $f$ est une densité de probabilité.
  2. X est une variable aléatoire de loi de densité $f$.
      Calculer :
    1. $P(X\leq 0,2)$
    2. $P(0.1< X \leq 0,5)$
    3. $P(X>0,2)$
    4. $P(X=0,5)$
    5. $P(-1<X<2)$
    6. $P(X\geq-5)$
correction de l'exercice 1

$g$ est la fonction définie sur $[0;+\infty[$ par : $$g(x)=2xe^{-x^2}.$$

  1. Pour tout nombre positif $a$, on pose : $$I(a)=\int_{0}^{a}g(x) dx.$$ Calculez $I(a)$ puis déduisez-en, $\lim\limits_{a\to +\infty} I(a)$.
  2. Justifiez que $g$ est une densité de probabilité.
  3. $X$ est une variable aléatoire qui suit la loi de densité $g$. Déterminez le nombre $m$ tel que $P(X\leq m)=0,5.$
correction de l'exercice 2

La fonction représentée ci-dessous définit une densité de probabilité sur $[-1;1]$.

Pour tout nombre $x$ tel que $-1\leq x\leq 1$, $$f(x)=a(1-x^2) \textrm{ avec a positif}.$$

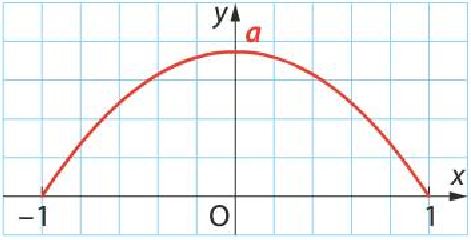
  1. Quelle est la valeur exacte de $a$ pour que $f$ soit une densité?
  2. $X$ est une variable aléatoire de loi de densité $f$.
    1. $P(X\geq t)=P(X\leq -t)$.
    2. $P(0\leq X \leq t)=\frac12-P(X\geq t)$.
correction de l'exercice 3

C'est l'exercice 3, le titre de la vidéo est trompeur !

On tire au hasard sur une cible de rayon 1 m sans jamais la manquer.

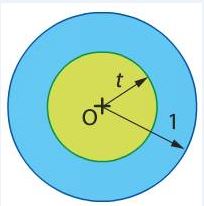
$X$ est la variable aléatoire qui donne la distance, en mètre , de l'impact au centre de la cible.

Ainsi $X$ prend ses valeurs dans l'intervalle $[0;1]$.

Selon le modèle usuel, pour tout $t$ de $[0;1]$, la probabilité de l'événement $"X\leq t"$ est défini par : $$P(X\leq t)=\frac{aire du disque de rayon t}{aire de la cible}.$$

  1. Pour tout $t$ de $[0;1]$, on pose $F(t)=P(X\leq t)^.$ Exprimez $F(t)$ en fonction de $t$.
  2. On note $f$ la densité sur $[0;1]$ de la loi de X.
    1. Écrivez $F(t)$ sous forme intégrale.
    2. Précisez la dérivée F.
    3. Déduisez-en l'expression de la densité $f$.
correction de l'exercice 4

Loi uniforme

X est une variable aléatoire qui suit la loi uniforme sur l'intervalle $[0;10]$. Calculez : $$P(X\leq 3) ;P(X>6);P(3<X<8).$$

correction de l'exercice 5
  • Une usine fabrique des tubes de diamètre 200mm. Le diamètre des pièces produites est une variable aléatoire qui suit une loi uniforme sur $[198;202]$. On choisit un tube au hasard.
  • Après contrôle, on le rejette si son diamètre D vérifie $D\leq 198.1$ ou $D\geq 201.9$.
  • Quelle est la probabilité que le tube soit rejeté?
    • correction de l'exercice 6

    Anne et Boris se donnent rendez-vous dans un café entre 12h00 et 13h00.

    Anne arrive à 12h20.

    On suppose que la durée (en min) entre midi et l'heure d'arrivée de Boris est une variable aléatoire uniformément répartie sur l'intervalle $[0;60]$.

    Calculez la probabilité que :

    1. Boris arrive avant Anne.
    2. Anne attende Boris plus de 20 minutes.
    3. Anne attende Boris moins de cinq minutes.
    correction de l'exercice 7

    Alix reçoit Ben entre 7h25 et 7h45 pour prendre un café avant de partir au lycée. Ben peut arriver à tout instant au hasard, uniquement dans cette plage horaire.

    1. Quelle densité de probabilité peut-on attribuer à la variable T qui indique l'instant d'arrivée (en minute) après 7h25 de Ben?
    2. Calculez la probabilité que Ben arrive chez Alix:
      1. à 7h30
      2. avant 7h30
      3. après 7h30
      4. entre 7h35 et 7h37
    3. En moyenne, sur un grand nombres de visites, à quelle heure arrive-t-il?
    correction de l'exercice 8

    $\mathcal{C}$ est dans un repère orthonormé, l'arc de parabole d'équation $y=x^2$ avec $-1\leq x\leq 1$.

    On choisit un nombre $t$ dans l'intervalle $[-1;1]$; ce choix se fait suivant la loi uniforme sur $[-1;1]$.

    M est le point de la courbe $\mathcal{C}$ d'abscisse t.

    On note S la variable aléatoire qui donne l'aire en u.a. du triangle ABM.

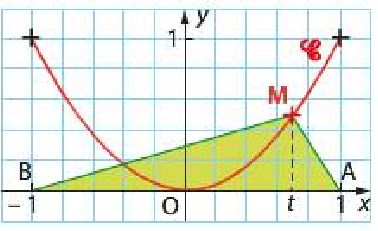
    1. Calculez : $$P(S\leq 0.25); P(S>0.5) ; P(S=1)$$
    2. Déterminez le nombre $\tau$ tel que : $P(S\leq \tau)=0,5$.
    correction de l'exercice 9

    Loi exponentielle

    Vrai ou Faux

    La durée de vie, exprimée en année , d'un appareil est modélisé par une variable aléatoire X qui suit une loi exponentielle de paramètre $\lambda=0,07$.

    1. La probabilité ( à $10^{-2}$ près ) que l'appareil ait une durée de vie supérieure à 10 ans est égale à 0,50.
    2. Sachant que l'appareil a fonctionné 10 ans, la probabilité (à $10^{-2}$ près ) qu'il fonctionne encore 5 ans est égale à 0,75.

    X désigne une variable aléatoire qui suit une loi exponentielle de paramètre $\lambda>0$.

    La courbe tracée ci-dessous représente la fonction densité $f$ associée.

      1. Quelle est la valeur de $\lambda$?
      2. Déduisez-en l'expression de $f(x)$.
      1. Quelle est la valeur exacte ( en u.a.) de l'aire sous la courbe de $f$ sur $[0;1]$? A quelle probabilité correspond cette aire?
      2. Calculez la valeur exacte $P(X>2)$. Interprétez graphiquement cette probabilité.
      3. Déduisez des calculs précédents la probabilité $P(1\leq X\leq 2)$ à $10^{-3}$ près.
      1. Quelle est l'espérance mathématique de X?
      2. Déduisez-en sans calcul $\lim\limits_{t\to +\infty} \int_{0}^{t}\lambda t e^{-\lambda x} dx.$

    La durée de vie T, exprimée en jour, d'un composant est une variable aléatoire qui suit la loi exponentielle de paramètre $\lambda=0,005$.

    Une année sera assimilée à 365 jours.

    1. Calculez à $10^{-3}$ près la probabilité de chacun des événements
      1. la durée de vie dépasse 300 jours.
      2. la durée de vie est d'au plus une année.
      3. la durée de vie est comprise entre 1 et 2 ans.
    2. La demi-vie de la loi T est la durée notée $t_{\frac12}$ telle que $P(T\leq t_{\frac12})=P(T>t_{\frac12})$.
      1. Justifiez que $t_{\frac12}$ vérifie $P(T\leq t_{\frac12})=0,5$
      2. Calculez à un jour près la valeur de $t_{\frac12}$.

    La durée d'attente X, exprimée en seconde, à un distributeur automatique est une variable aléatoire qui suit une loi exponentielle de paramètre $\lambda>0$. La probabilité que l'attente dépasse une minute est $0,942$.

    Les résultats seront arrondis à $10^{-3}$ près.

    1. Calculez une valeur approchée de $\lambda$.
    2. Calculez la probabilité que l'attente dure entre 4 et 5 minutes.

    Un système électronique est constitué de trois composants montés en série.

    La durée de vie, exprimée en heure, de ces composants sont indépendantes et suivent la loi exponentielle de paramètre $\lambda=10^{-4}$.

    On note p la probabilité qu'un composant de ce type fonctionne au moins 1000 heures.

    1. Prouvez que $p=e^{-0,1}$.
    2. On note S l'événement "Le système fonctionne au moins 1000 heures".
      1. Exprimez $P(S)$ en fonction du nombre p.
      2. Déduisez-en une valeur approchée, à $10^{-3}$ près, de la probabilité de S.

    X est une variable aléatoire qui suit une loi exponentielle de paramètre $\lambda$.

    1. Déterminez en fonction de $\lambda$ la valeur $t_{\frac12}$ telle que : $$P(X\leq t_{\frac12})=P(X>t_{\frac12}).$$
    2. On suppose que $t_\frac12=99$. Calculez $P(100\leq X\leq 200)$.

    Loi normale

    La variable $Z$ suit la loi $\mathcal{N}(0;1).$

    1. Déterminez $P(Z <-2,3)$ et $P(Z<2,9)$ avec une calculatrice, avec trois décimales.
    2. Déduisez-en, sans outil de calcul : $$P(Z\geq -2,3); P(Z>2,9);$$ $$P(-2,3\leq Z\leq 2,9);P(Z<-2,3 ou Z>2,9).$$

    La variable $Z$ suit la loi $\mathcal{N}(0;1).$ Calculez :

    1. $P(-1,2<Z<1,2)$
    2. $P(Z<-1,2 ou Z>1,2)$

    Sous la courbe de Gauss ci-dessous, les deux droites verticales délimitent trois domaines.

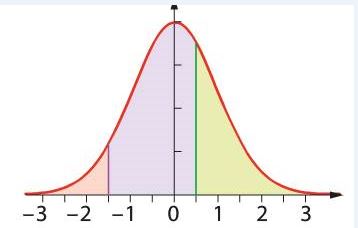
    Déterminez leur aires respectives, à $10^{-2}$ près.

    Déterminez $u_{0,4}$ avec deux décimales.

    Z est une variable aléatoire qui suit la loi normale standard.

    Déterminez l'intervalle ouvert I de centre 0 tel que $P(X\in I)=0,7$.

    Vous donnerez les bornes de I avec trois décimales.

    Z est une variable aléatoire qui suit la loi normale standard.

    Déterminez l'intervalle ouvert I de centre 0 tel que $P(X\notin I)=\frac13$.

    Vous donnerez les bornes de I avec deux décimales.

    La variable aléatoire $X$ suit une loi normale $\mathcal{N}(20;5)$. Calculer les probabilités suivantes :

    1. $P(X\leq28)$ ;
    2. $P(X\geq28)$ ;
    3. $P(X\geq12)$ ;
    4. $P(X\leq12)$ ;
    5. $P(12\leq X\leq 28)$.

    Une entreprise produit des bouteilles d'eau minérale de 1,5 L.

    Une bouteille d'eau sortant de la chaîne de remplissage est considérée bonne si elle contient entre 149,6 cl d'eau et 150,4 cl d'eau.

    On note $C$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée, associe son contenu en centilitres.

    On suppose que C suit la loi normale de moyenne 150 et d'écart type 0,2. Déterminez à $10^{-3}$ près la probabilité qu'une bouteille soit bonne.

    La variable aléatoire $X$ suit une loi normale $\mathcal{N}(20;5)$. Déterminer à $10^{-2}$ près le nombre réel $a$ tel que :

    1. $P(X\leq a)=0,99$ ;
    2. $P(X\leq a)=0,01$ ;
    3. $P(X\geq a)=0,05$ ;
    4. $P(X\geq a)=0,90$ ;
    5. $P(20-a\leq X\leq 20+a)=0,95$.

    (les résultats seront arrondis à $10^{-2}$).

    On désigne par $X$ une variable aléatoire.

    1. $X$ suit une loi normale $\mathcal{N}(2;0,1)$, calculer $P(X~\geq~2,2)$.
    2. $X$ suit une loi normale $\mathcal{N}(m;0,1)$.
      1. Calculer $m$ pour que $P(X\geq2,2)=0,05$.
      2. Calculer $m$ pour que $P(X\geq2,2)=0,95$.
    3. $X$ suit une loi normale $\mathcal{N}(2;\sigma)$.
      1. Calculer $\sigma$ pour que $P(X\leq2,2)=0,9$.
      2. Calculer $\sigma$ pour que $P(1,8\leq X\leq 2,2)=0,9$.

    Un producteur de pamplemousses a constaté que le diamètre des fruits arrivés à maturité était en moyenne de 12 cm, avec un écart-type de 3 cm.

    En supposant que le diamètre suit une loi normale, quelle est la proportion de pamplemousses dont le diamètre est :

    1. inférieur à 11cm?
    2. compris entre 11 et 14 cm?
    3. supérieur à 14 cm?

    Une machine produit des clous dont la longueur moyenne est 12mm, avec un écart-type de 0,2mm.

    La longueur L d'un clou pris au hasard est une variable aléatoire qui suit la loi normale.

    Un clou est jugé défectueux si sa longueur est supérieure à 12,5 mm ou inférieure à 11,5 mm.

    1. Quelle est la proportion de clous défectueux?
    2. Pour un clou défectueux pris au hasard, quelle est la probabilité que sa longueur soit inférieure à 11,5mm?

    Au pôle Nord, la température en hiver suit approximativement une loi normale de moyenne -34 et d'écart-type 5. Sur 180 jours d'hiver, pendant combien de jours peut-on s'attendre à ce que la température soit :

    1. inférieure à -40°?
    2. supérieure à -30°?

    Dans un supermarché, le gérant a établi une statistique de ses ventes quotidiennes de packs d'eau minérale. Il apparait que le nombre X de packs vendus chaque jour suit une loi normale de moyenne 52 et d'écart-type 12.

    1. Le gérant ne peut stocker plus de 76 packs dans sa reserve. Avec un tel stock, quelle serait la probabilité qu'un jour donné il ne puisse pas répondre à la demande? ( rupture de stock ).
    2. Il ne souhaite pas remplir complètement la réserve, car cela rend la manutention difficile. Mais il voudrait limiter à 5$\%$ le risque de rupture de stock. Quel doit être son stock quotidien?

    Synthèse

    Une entreprise d'autocars dessert une région montagneuse. En chemin, les véhicules peuvent être bloqués par des incidents extérieurs ( chutes de pierres, présence de trous sur la route, verglas etc.).

    Un autocar part du dépôt. On note D la variable aléatoire qui mesure la distance, en km, que l'autocar va parcourir jusqu'à ce que survienne un incident. On admet que D suit la loi exponentielle de paramètre $\lambda=\frac{1}{82}$.

    Les résultats demandés seront arrondis à $10^{-3}$ près.

    1. Calculez la probabilité que la distance parcourue sans incident soit :
      1. comprise entre 50 et 100 km
      2. supérieure à 300km.
    2. Sachant que l'autocar a déjà parcouru 300 km sans incident, quelle est la probabilité qu'il n'en subisse pas non plus au cours des 25 prochains kilomètres?
    3. Quelle est la distance moyenne $d_m$ parcourue sans incident?
    4. L'entreprise possède 96 autocars. Les distances parcourues par chacun d'eux sont des variables aléatoires de même loi exponentielle vue ci-dessus. Les incidents qui peuvent survenir aux autocars sont indépendants les uns et des autres. Pour tout nombre $d>0$, $X_d$ désigne la variable aléatoire qui donne le nombre d'autocars n'ayant subi aucun incident après avoir parcouru $d$ kilomètres.
      1. Quelle est la loi de la variable aléatoire $X_{d_m}$?
      2. Quel est, à une unité près, le nombre moyen d'autocars n'ayant subi aucun incident après avoir parcouru $d_m$ kilomètres?

    Une enquête a montré que $50\%$ des élèves du lycée Delacour utilisent quotidienement un ordinateur. On interroge successivement et de manière indépendante 64 élèves de ce lycée choisis au hasard et "avec remise". On note X la variable aléatoire qui comptabilise ceux qui utilisent quotidiennement un ordinateur.

    1. Justifiez que la loi de probabilité de X est une loi binomiale et précisez les paramètres de cette loi.
    2. Justifiez que cette loi peut être approchée par une loi normale dont vous préciserez les paramètres.
    3. Calculez la probabilité qu'au plus 36 élèves utilisent quotidiennement un ordinateur.

    1. On a représenté ci-contre la courbe de Gauss.

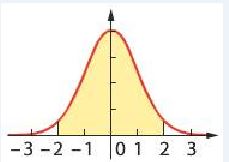
      A $10^{-2}$ près, l'aire du domaine colorié vaut :

      1. 0,68
      2. 0,95
      3. 1
    2. A $10^{-3}$ près :
      1. $u_{0,4}\approx 0,345$
      2. $u_{0,4}\approx 0,645$
      3. $u_{0,4}\approx 0,842$
    3. Si la variable aléatoire X suit la loi $\mathcal{N}(2000;10000)$, alors , à $10^{-3}$ près :
      1. $P(1800\leq X\leq 2200)\approx 0,683.$
      2. $P(1800\leq X\leq 2200)\approx 0,954.$
      3. $P(1800\leq X\leq 2200)\approx 0,997.$
    4. X est une variable aléatoire qui suit la loi $\mathcal{N}(15;0,25)$.
      1. $P(14\leq X<15) \approx 0,68$.
      2. $2X-30$ suit la loi $\mathcal{N}(0;1)$.
      3. $P(X\leq 16) \approx 0,4$
    5. X est une variable aléatoire qui suit la loi $\mathcal{B}(25;0,1)$.
      1. $P(X<12)=P(X\leq 12)$.
      2. $P(X>12)=P(X>12,5)$.
      3. X suit sensiblement la loi $\mathcal{N}(2,5;1,5)$.
    Licence Creative Commons
    Maths et Informatique à Saint Dizier de Thomas Lourdet et de Pascal Thérèse enseignants au lycée Blaise Pascal de Saint Dizier (52) est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.