Comment, la diversité des éléments chimiques est-elle apparue ? Et pourquoi tous les noyaux d'atomes n'ont pas le même âge?
Au programme:
Le document à compléter est téléchargeable ici
Abondance relative des éléments chimiques
Formation de l'univers
Le Big Bang (« Grand Boum ») est un modèle cosmologique utilisé par les scientifiques pour décrire l'origine et l'évolution de l'Univers.
De façon générale, le terme « Big Bang » est associé à toutes les théories qui décrivent notre Univers comme issu d'une expansion rapide il y a 13,8 milliards d’années,
sans que cela préjuge de l’existence d’un « instant initial » ou d’un commencement à son histoire.
Afin de repérer les principales étapes de cette théorie, regardez la première vidéo (vous regarderez la seconde à la maison lors de vos révisions)
Abondance des éléments
L'abondance des éléments chimiques est la mesure de la proportion de ces éléments dans un environnement donné par rapport aux autres éléments.
Le tableau ci-dessous nous montre l'abondance relative des éléments chimiques dans l'univers, le soleil, la croûte terrestre, l'atmosphère terrestre,
l'eau de mer, le corps humain et les végétaux.
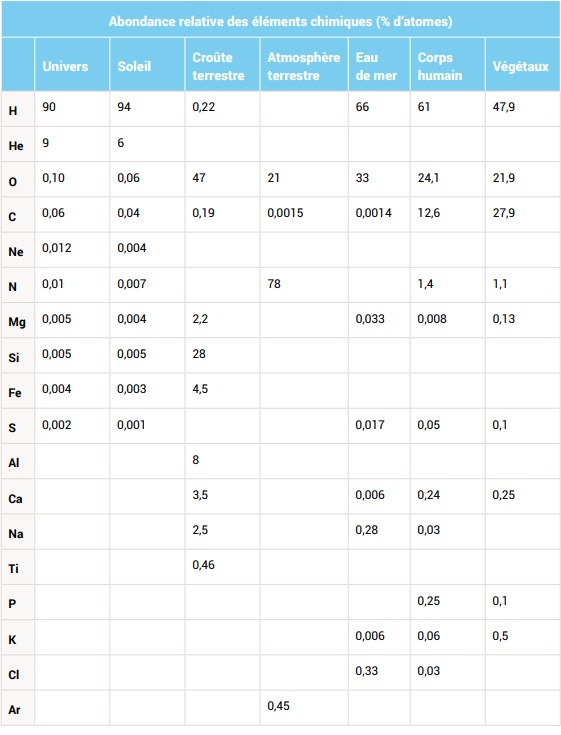
Dans le tableau ci-dessus on remarque que la lecture des informations n'est pas évidente, il est préférable d'utiliser des représentations graphiques, comme par exemple le diagramme circulaire, le diagramme en barres, ...
A l'aide d'un tableur grapheur, représenter sous forme d'un diagramme circulaire les abondances relatives des éléments chimiques présents dans la croûte terrestre.
Les éléments dont le pourcentage est inférieur à 1 seront additionnés et regroupés dans une catégorie que nous appellerons "autres éléments".
Appel professeur pour lui présenter votre graphique
Exercice de 
Exercice de
A l'aide du langage Python, nous allons programmer la visualisation des abondances relatives des éléments chimiques présents dans le corps humain (voir tableau).
Les éléments dont le pourcentage est inférieur à 1 seront additionnés et regroupés dans une catégorie que nous appellerons "autres éléments".
Dans le trinket ci-dessous, modifier le script Python puis cliquez sur run pour visualiser votre diagramme.
Appel professeur pour lui présenter votre graphique
Pour aller plus loin.
-
Vidéo : 10 THÉORIES sur la NAISSANCE de l'UNIVERS
-
Il est également possible de réaliser ce type de diagramme à l'aide de certaines calculatrices, entraînez-vous à la maison. Vous trouverez ci-dessous un tutoriel pour les calculatrices de la marque Casio.
Transformations nucléaires dans l'univers
Dans les étoiles : les réactions de fusion
La fusion nucléaire est le processus dans lequel deux noyaux atomiques s’assemblent pour former un noyau plus lourd.
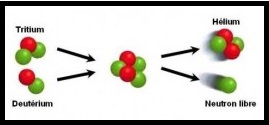
Dans cette réaction de fusion, deux noyaux très légers le deutérium et le tritium (deux isotopes de
l’hydrogène) se combinent en un noyau plus lourd l’hélium : $_1^2H+_1^3H → _2^4He+ _0^1n$
Parmi les transformations nucléaires suivantes, identifier celles qui mettent en jeu le processus de fusion nucléaire.
-
$_0^1n+ _{92}^{235} U → _{39}^{94} Y+ _{53}^{139}I + 3 _0^1n$
-
$_1^2H+_1^3H → _2^4He+ _0^1n$
-
$_{53}^{131} I → _{54}^{131} Xe+ _{-1}^0e$
-
$_2^3He+_2^3He → _2^4He+ 2 _1^1H$
-
$_0^1n+ _{94}^{239} Pu → _{52}^{135} Te+ _{42}^{102}Mo + 3 _0^1n$
Exercice de 
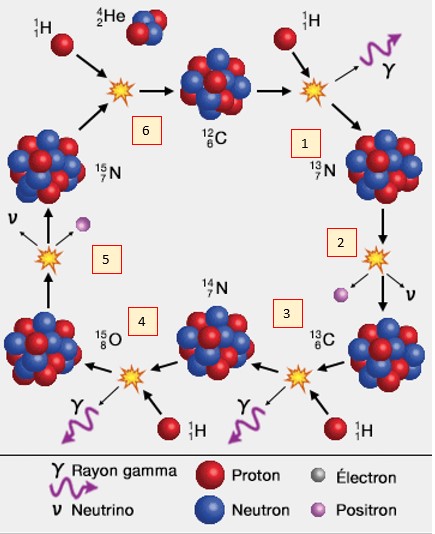
Le cycle CNO, pour Carbon (Carbone), Nitrogen (Azote), Oxygene, (Oxygène) en anglais, est l'un des cycles de transformations nucléaires faisant briller les étoiles.
Il a été découvert à la fin des années 30 au siècle dernier par le prix Nobel Hans Bethe.
Dans ce cycle on peut identifier six transformations (numérotées sur le schéma). Identifier celles qui mettent en jeu le processus de fusion nucléaire.
Sur terre, la fusion nucléaire est utilisée dans les bombes H, dans les générateurs de neutrons,
et dans les années à venir dans la production d'électricité, si on en croit le Royaume-Uni qui a mis en marche son réacteur à fusion le 29 octobre 2020.
Sur terre : les réactions de fission
La fission nucléaire est le processus dans lequel un noyau lourd se brise en deux noyaux plus légers.
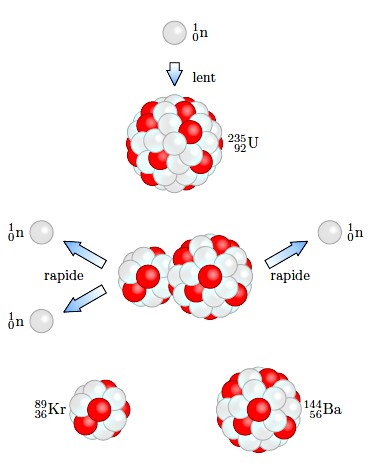
Dans cette réaction de fission, un noyau lourd l'uranium 235 est bombardé par un neutron et se brise en deux noyaux plus légers un de krypton et un de baryum et
libère aussi trois neutrons : $_0^1n+ _{92}^{235} U → _{36}^{93} Kr+ _{56}^{140}Ba + 3 _0^1n$
Parmi les transformations nucléaires suivantes, identifier celles qui mettent en jeu le processus de fission nucléaire.
-
$_0^1n+ _{92}^{235} U → _{39}^{94} Y+ _{53}^{139}I + 3 _0^1n$
-
$_1^2H+_1^3H → _2^4He+ _0^1n$
-
$_0^1n+ _{94}^{239} Pu → _{52}^{135} Te+ _{42}^{102}Mo + 3 _0^1n$
-
$_2^3He+_2^3He → _2^4He+ 2 _1^1H$
-
$_{53}^{131} I → _{54}^{131} Xe+ _{-1}^0e$
Exercice de 
Sur terre, la fission nucléaire est utilisée par exemple pour la propulsion des navires de guerre, dans les centrales électriques
(en France par exemple on utilise commme combustible fissile l'uranium 235), ...
Sur terre: la radioactivité naturelle
-
Documents
-
Document 1 : la radioactivité
Dans la nature, la plupart des noyaux d’atomes sont stables.
Cependant, certains atomes ont des noyaux instables,
ce qui est dû à un excès soit de protons, soit de neutrons, ou encore à un excès des deux. Ils sont dits radioactifs et sont appelés radio-isotopes ou radionucléides.
La radioactivité a été découverte, il y a un peu plus d’un siècle, en 1896, par le physicien français Henri Becquerel (qui donna son nom à une unité de mesure en radioactivité).
Les noyaux d’atomes radioactifs se transforment spontanément en d’autres noyaux d’atomes, radioactifs ou non. Ainsi, de noyau radioactif en noyau radioactif,
l’uranium 238 tend à se transformer en une forme stable, le plomb 206. Cette transformation irréversible d’un atome radioactif en un autre atome est appelée désintégration.
Elle s’accompagne d’une émission de différents types de rayonnements.
-
Document 2 : Texte d'Henri Becquerel
« Une plaque photographique a été enfermée dans un châssis opaque, fermé d’un côté par une plaque d’aluminium : si l’on exposait le châssis en plein soleil, la plaque ne serait pas voilée.
Cependant, si l’on vient à fixer sur la plaque d’aluminium, à l’extérieur, une lamelle de sel d’uranium et si l’on expose le tout pendant plusieurs heures au soleil, on reconnaît,
lorsqu’on développe ensuite la plaque par des procédés ordinaires, que la silhouette de la lamelle cristalline apparaît en noir sur la plaque sensible.
Parmi les expériences qui précèdent, quelques-unes avaient été préparées le mercredi 26 et le jeudi 27 février.
J’avais conservé les expériences toutes préparées et rentré les châssis à l’obscurité en laissant en place les lamelles du sel d’uranium.
Le soleil ne s’étant pas montré les jours suivants, j’ai développé les plaques photographiques le premier mars, en m’attendant à trouver des images très faibles.
Les silhouettes apparurent, au contraire, avec une grande intensité. »
Henri Becquerel, note à l’Académie des sciences, 1896.
Plaque photographique d’Henri Becquerel : on y distingue les contours d’une croix en cuivre qu’il avait placée entre les sels d’uranium et la plaque sensible
-
Questions
-
Qu'est-ce que la radioactivité ?
-
Qu'est-ce qu'une désintégration ?
-
Est-ce la lumière solaire qui impressionne la plaque photo dans l’expérience de Becquerel ?
-
D’où provient le rayonnement qui impressionne la plaque photo ?
-
Documents
-
Document 3 : la désintégration radioactive
Lorsqu'un noyau est instable*, il est susceptible de se désintégrer. Pour un noyau donné il est toutefois impossible de prédire la date de la désintégration. On peut simplement donner la probabilité
pour que ce noyau se désintègre entre les instants $t$ et $t+dt$. On dit que la désintégration présente un caractère probabiliste. La probabilité est la même pour des noyaux identiques.
Un noyau instable ne "vieillit" pas : sa probabilité de se désintégrer reste la même au cours du temps.
On peut comparer cela au lancer d'une pièce de monnaie : la probabilité d'obtenir pile ou face reste de 1/2 pour chaque lancer quel que soit le nombre d'essais effectués,
et il est impossible de prédire au bout de combien de lancers la pièce retombera côté pile.
-
Document 4 : la demi-vie
La demi-vie T (également appelée période radioactive) est la durée au bout de laquelle le nombre de noyaux radioactifs restant est égal à la moitié du nombre de noyaux initial de l'échantillon.
Détermination graphique de la demi-vie:
-
Application : Nous allons simuler la désintégration radioactive grâce à des pièces de monnaies.
Plus vous aurez de pièces de monnaies à disposition, plus vous serez proche de la réalité de la loi de décroissance radioactive.
-
Prendre des pièces de monnaie. Les jeter sur une table, toutes les pièces tombées côté face seront considérées comme désexcitées et retirées du lancer suivant.
Les pièces tombées côté pile seront considérées comme toujours radioactives et gardées pour le lancer suivant.
Remplir le tableau suivant en comptant le nombre de pièces tombées côté pile à chaque lancer (le lancer 0 correspond au nombre de pièces initiales,
car nous considérons qu'au départ toutes les pièces sont côté pile).
| Lancer n° |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Pièces tombées côté pile |
|
|
|
|
|
|
|
|
|
|
|
-
Tracer la courbe sur Excel correspondant au nombre de pièces tombées côté pile en fonction du numéro du lancer.
-
On va modéliser l'expérience et considérer qu’entre chaque lancer le temps est équivalent à 1 heure.
Déterminer graphiquement le temps de demi-vie pour cette simulation de courbe de décroissance radioactive.
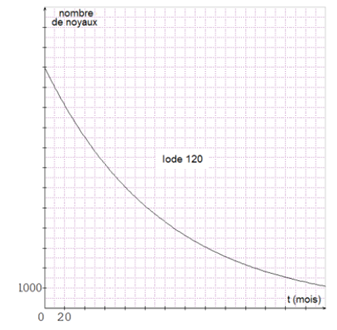
On considère l'évolution d'une population de 12 000 noyaux d'iode 120
-
Déterminer la demi-vie de l’iode 120.
-
Combien de noyaux restera-t-il au bout de 2 demi-vies ?
-
Même question pour 3 demi-vies.
Exercice de 
Le technetium-99m est un élément radioactif utilisé en médecine nucléaire pour diagnostiquer une embolie pulmonaire.
Sa demi-vie est $t_{\frac{1}{2}}=6$ heures. Une dose contenant $N_0=2,4 \times 10 ^{13}$ noyaux de technetium-99m est injectée à un patient devant subir un examen des poumons.
-
Déterminer le nombre de noyaux radioactifs encore présents dans l'organisme au bout de 12 heures
-
Calculer au bout de combien de temps il ne reste dans l'organisme que $N=1,5 \times 10 ^{12}$ noyaux de technetium-99.
Pour aller plus loin.
Une application : la datation au carbone 14
Généralités
Le carbone-14 est un isotope radioactif de l’élément carbone. Avec le temps, le carbone-14 se transforme en azote-14 qui est stable et s’envole dans l’air ambiant.
(Sur 1000 milliards d’atomes de carbone dans l’atmosphère, on aurait environ 999 999 999 999 atomes de carbone-12 et un seul atome de carbone-14 !)
En respirant et en mangeant, les plantes et les animaux absorbent de toutes petites quantités de carbone-14. Tous les êtres vivants contiennent donc un peu de carbone-14,
nous y compris ! Et tant qu’on vit, cette proportion de carbone-14 par rapport au carbone-12 correspond à celle qu’on retrouve dans l’atmosphère (1 pour 999 999 999 999).
Mais lorsqu’on meurt, on ne mange plus. Tout ce carbone cesse alors de se renouveler et le carbone-14 de notre corps commence à disparaitre tout doucement.
Un petit jeu pour débuter.
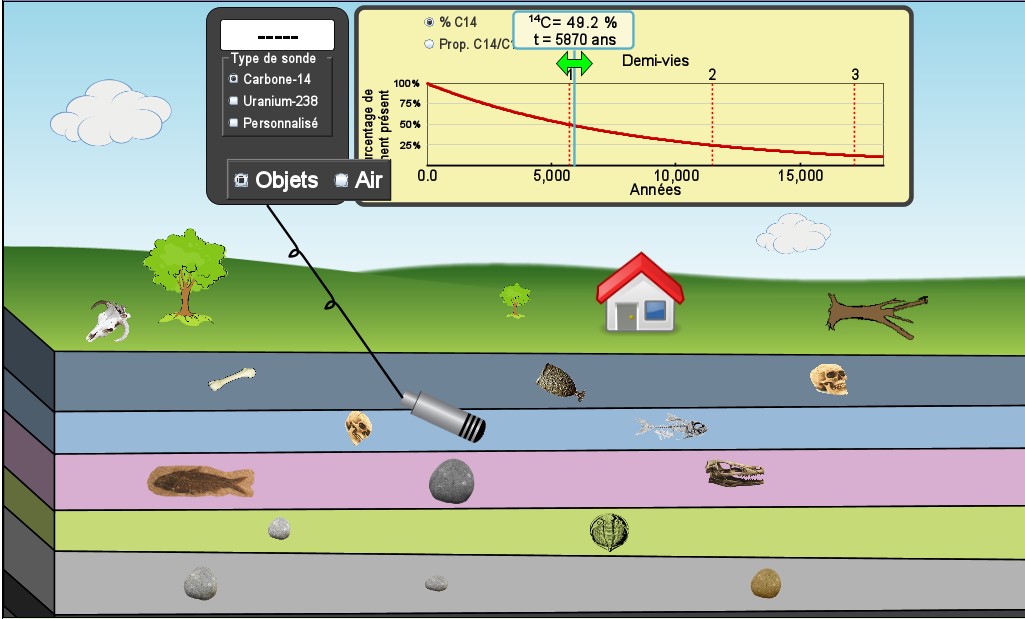
-
Lancer l'animation (au besoin cliquer sur l'onglet "Jeu de datation").
-
En déplaçant la sonde avec votre souris, puis en bougeant le curseur jaune du graphique, déterminer l'âge de quelques éléments en bois, par exemple :
la coupe en bois, l'arbre mort et l'arbre vivant, ...
-
Faire la même chose avec les pierres. Conclure.
-
Renouveler une dernière fois cette manipulation avec le crâne humain de la couche supérieure et le crâne de dinosaure. Conclure
-
Expliquer comment on arrive à dater les différents éléments dans ce jeu.
Pour aller plus loin.
Le script ci-dessous permet de simuler la désintégration d'un radionucléide en tirant au hasard "1" ou "2" (c'est notre pile ou face de l'expérience précédente).
-
Identifier où a lieu ce tirage.
-
Est-ce la valeur "1" ou la valeur "2" qui correspond au noyau désintégré?
-
Compléter les commentaires manquants. Lien vers la documentation mathplotlib
Renforcement
A l'aide d'un tableur grapheur, représenter sous forme d'un diagramme circulaire les abondances relatives des éléments chimiques présents dans le corps humain.
Les éléments dont le pourcentage est inférieur à 1 seront additionnés et regroupés dans une catégorie que nous appellerons "autres éléments".
A l'aide d'un tableur grapheur, représenter sous forme d'un diagramme en barres les abondances relatives des éléments chimiques présents dans l'univers.
Les éléments dont le pourcentage est inférieur à 1 seront additionnés et regroupés dans une catégorie que nous appellerons "autres éléments".
Parmi les transformations nucléaires suivantes, identifier celles qui mettent en jeu le processus de fusion nucléaire.
-
$ _{6}^{12}C + _{6}^{12}C → _{2}^{4} He+ _{10}^{20}Ne$
-
$ _{8}^{16}O + _{8}^{16}O → _{2}^{4} He+ _{14}^{28}Si$
-
$_{26}^{56}Fe → 13 _{2}^{4} He+ 4 _{0}^{1} n$
-
$ _{24}^{48}Cr + _{2}^{4}He → _{26}^{56}Fe$
-
$_{10}^{20} Ne → _{2}^{4} He+_{8}^{16}O$
-
$_{26}^{56}Fe + _{2}^{4}He → _{28}^{60} Ni$
Les transformations 1, 2, 4 et 6 mettent en jeu le processus de fusion nucléaire.
Parmi les transformations nucléaires suivantes, identifier celles qui mettent en jeu le processus de fission nucléaire.
-
$ _{6}^{12}C + _{6}^{12}C → _{2}^{4} He+ _{10}^{20}Ne$
-
$ _{8}^{16}O + _{8}^{16}O → _{2}^{4} He+ _{14}^{28}Si$
-
$_{26}^{56}Fe → 13 _{2}^{4} He+ 4 _{0}^{1} n$
-
$ _{24}^{48}Cr + _{2}^{4}He → _{26}^{56}Fe$
-
$_{10}^{20} Ne → _{2}^{4} He+_{8}^{16}O$
-
$_{26}^{56}Fe + _{2}^{4}He → _{28}^{60} Ni$
La transformation 5 met en jeu le processus de fission nucléaire.
On considère la courbe de décroissance radioactive du césium-137.
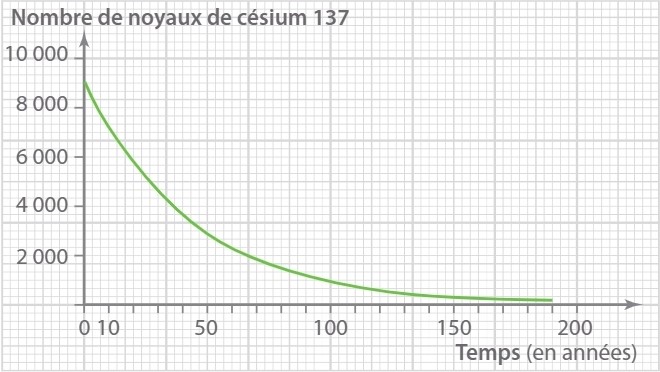
-
Déterminer graphiquement le temps de demi-vie
-
Combien reste t-il de noyaux au bout de deux demi-vies.
Préparation EC
QCM
Vers le bac
La scintigraphie
La scintigraphie est une méthode d'imagerie médicale de médecine nucléaire qui produit une image fonctionnelle
par l'administration d'un médicament radiopharmaceutique (MRP) dont on détecte les rayonnements une fois qu'il a été capté par l'organe ou la cible à examiner.
La thyroïde est une glande endocrine située à l'avant du cou et sécrétant des hormones essentielles au bon fonctionnement de l'organisme.
Une patiente souffrant de troubles thyroïdiens doit pratiquer une scintigraphie. De l'iode 123 lui est injecté par intraveineuse une heure avant l'examen.
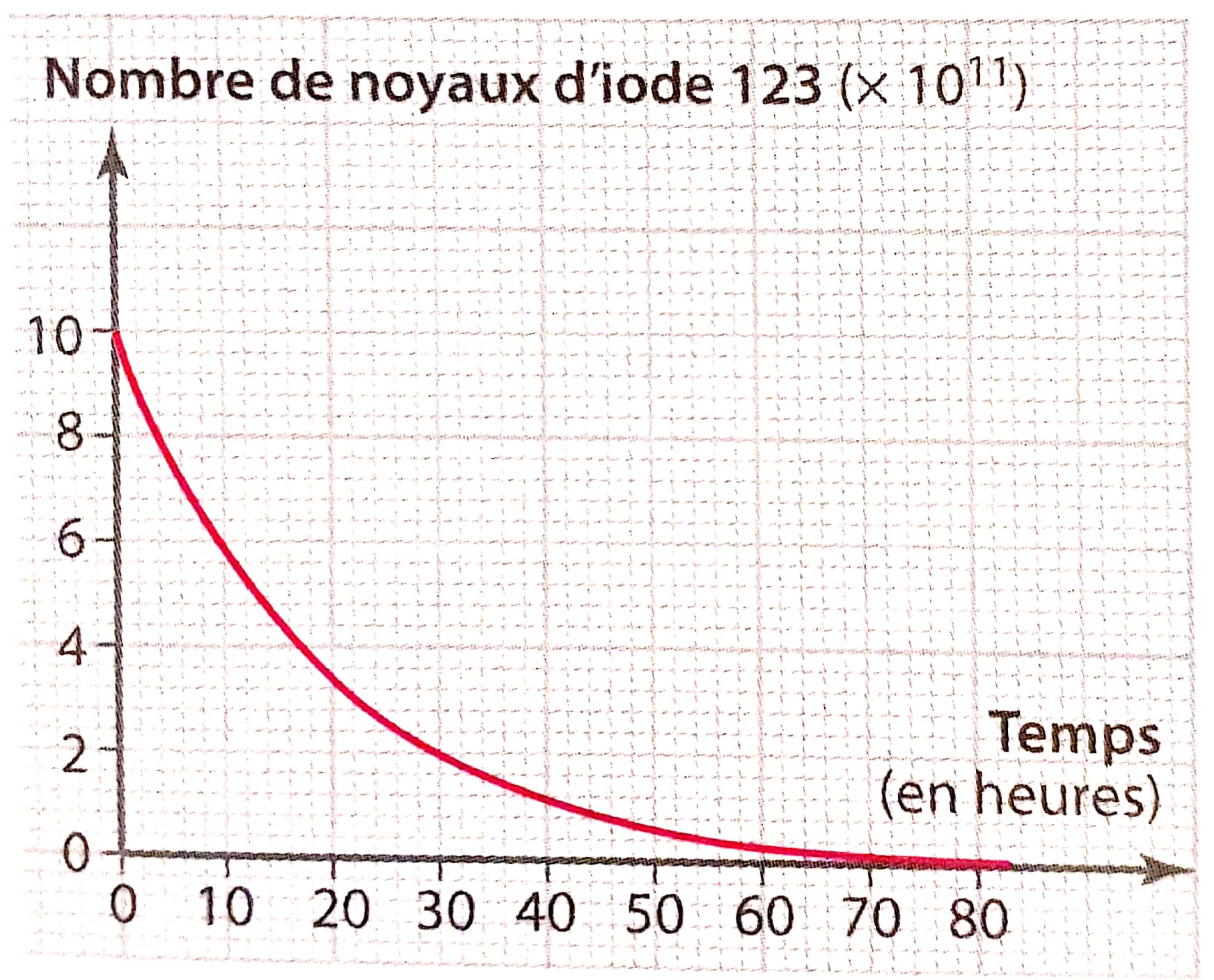
-
Pourquoi utilise-t-on des doses limitées de produits radioactifs lors d'une scintigraphie ?
-
Combien de noyaux radioactifs d'iode 123 ont été injectés à la patiente? Déterminer graphiquement la demi-vie de l'iode 123.
-
Calculer le nombre de noyaux d'iode 123 restant au bout de trois demi-vies.
-
Déterminer la durée au bout de laquelle il ne reste qu'un dixième du nombre initial des noyaux injectés.