Comment peut-on à l’aide d’un logiciel créer un son et visualiser son spectre pour l'identifier ?

Objectifs de la séance:

• Apporter des connaissances numériques pour « le projet expérimental et numérique »
• Réinvestir les connaissances de début de séquence.
• Utiliser un logiciel permettant de visualiser le spectre d’un son.
• Utiliser un logiciel pour produire des sons purs et composés.
• Relier qualitativement la fréquence fondamentale du signal émis et la longueur d’une corde vibrante.

Documents

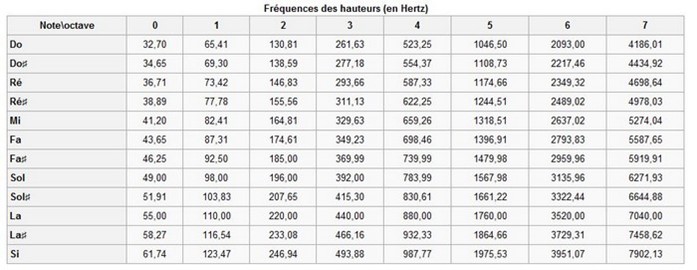
Document 1 : Fréquences des différentes notes (source Wikipédia)

Document 2 : Notice simplifiée d’Audacity

1. Acquérir un son via le micro de l’ordinateur

   
   

   • Choisir comme source « microphone »:

     
     

   • L’enregistrement débute après avoir cliqué sur l’icône :

     
     

   • Pour stopper l’enregistrement cliquer sur l’icône STOP :

     
     

   • Avec l’outil de sélection , on peut sélectionner une partie inutile sur signal et la supprimer (touche suppr)

     
     

2. Ouvrir un fichier son

   
   

   • On peut ouvrir un fichier audio préalablement enregistré : Fichier => Ouvrir (ou CTRL + O)

     
     

3. Sélection et zoom

   
   

   • Il est possible de choisir une portion de l’enregistrement en cliquant sur l’outil de sélection. Ensuite on sélectionne la partie souhaitée avec la souris

     
     

   • L’outil zoom permet de modifier l’échelle des temps (axe des abscisses). Clic gauche : zoom avant ; clic gauche pour zoom arrière.

     
     

4. Analyse du spectre d’un son

   
   

   • Sélectionner une partie de l’enregistrement, avec l’outil sélection.

     
     

   • Cliquer sur Analyse puis Tracer le spectre. Choisir les réglages ci-dessous.

     
     

   • Le relevé des valeurs des fréquences des harmoniques s’effectue en déplaçant la flèche de la souris à proximité d’un pic, la valeur de la fréquence du pic est indiquée par « Pic » en bas à droite du spectre.

     
     

Document 3 : Les bases de Python

Lien vers les bases de Python pour la physique

Document 4 : Les fonctions sinusoïdales

Une courbe est dite sinusoïdale si son allure est du type :

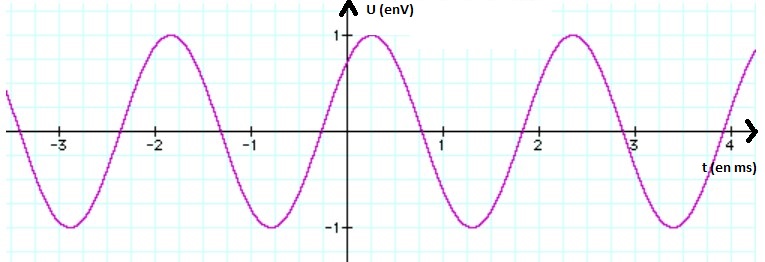
Cette courbe est représentative des sons purs et est du type U=a.sin(ωt + φ), ici la courbe représentée est U = sin(3t + π/4).

Une courbe plus complexe, correspondant à un son composé peut être obtenue par addition de plusieurs courbes sinusoïdales :

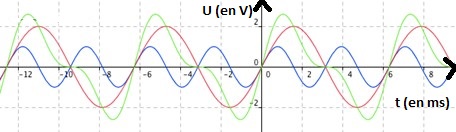
courbe_verte(t)= courbe_rouge(t) + courbe_bleue(t)

Document 5 : Les modules wave et math

Une des grandes forces du langage Python réside dans le nombre important de bibliothèques logicielles externes disponibles. Une bibliothèque est un ensemble de fonctions, qui permettent de faire : du calcul numérique, du graphisme, ...

• Le module wave permet de générer des sons à l’aide de Python.

  Le module est appelé à l’aide de la syntaxe :

  import wave

  Lorsque vous lancerez votre programme, le son sera créé dans le dossier où se trouve le programme Python. Si un son du même nom existe déjà, il sera remplacé, sinon il sera créé.

  Vous n'avez pas besoin d'en savoir plus sur wave, l'objectif ici n'étant pas de faire de la programmation.

• Le module math permet d’utiliser des éléments mathématiques qui ne sont pas natifs dans Python, comme pi, la fonction sinus, ……

  Le module est appelé à l’aide de la syntaxe :

  import math

  Pour utiliser pi, je devrais écrire :

  math.pi

  Pour calculer sin(t) , je devrais écrire :

  math.sin(t)

Travail à réaliser

Vous trouverez dans cette partie le travail à faire, vous devez compléter au fur et à mesure le document réponse (téléchargeable ci-dessous).

Des aides sont disponibles sur demande après vérification d’un blocage, n’hésitez pas à m'appeler!

Les différents documents et programmes sont téléchargeables en un seul fichier .zip ici Vous devez ensuite placer le fichier décompressé sur le bureau de votre ordinateur ( Vous pouvez regarder la vidéo d'aide ci-dessous en cas de besoin).

Question 1

• Ouvrir le programme generateur_son_eleve.py dans édupython.

• Afin de comprendre le programme, complétez les quelques commentaires manquants.

Code de déblocage de l'aide :

• Enfin modifiez le programme pour générer un La₃

Code de déblocage de l'aide :

Question 2

• Recopier la ou les ligne(s) modifiée(s).

Question 3

• A l’aide du logiciel Audacity, nous allons vérifier que le son créé est bien un La₃.

• Dans un premier temps réaliser un protocole permettant de réaliser cette tâche.

Code de déblocage de l'aide :

!! Appel professeur n°1 : Présentation de votre protocole !!

• Réaliser ce protocole

Question 4

• Ouvrir maintenant le programme generateur_son_2_eleve.py

• Que fait ce programme ?

Code de déblocage de l'aide :

Question 5

• Créer un son à partir de ce programme

• Vérifiez votre réponse à la question précédente

!! Appel professeur n°1 : Présentation de vos résultats !!

Question 6

• Application :

  Dans la vidéo ci-dessous, Renaud joue trois notes à la guitare en réduisant à chaque fois la longueur de la corde par deux (la corde de départ mesure 64 cm).

A l’aide des sons contenus Dans le dossier "sons_a_etudier", complétez le tableau suivant:

Nom	son_1	son_2	son_3
Longueur de la corde (en cm)
Son pur (oui ou non)
Fréquence fondamentale (en Hertz)

• Que peut-on conclure?

Code de déblocage de la correction :

Pour aller plus loin

Pour les plus rapides, chercher comment réaliser le spectre d’un son à l’aide du tableur scientifique « regressi », et vérifier à l’aide des sons créés précédemment.