En BTS CIEL, il est important de savoir effectuer à la main les calculs élémentaires de mathématiques et aussi de savoir utiliser l'outil informatique pour réaliser des calculs plus complexes et pour conjecturer des résultats.

Dans ce premier chapitre, vous apprendrez à utiliser Xcas pour modifier une expression, pour résoudre des équations et des systèmes ainsi que Geogebra pour représenter des fonctions.

Modifier une expression

Développer une expression

Pour développer à la main une expression, penser à utiliser une des deux idées suivantes :

  1. la distributivité (simple ou double),

  2. les identités remarquables.

Ne pas hésiter à écrire les flèches si besoin lorsque vous développez.

Développer les expressions suivantes :

  1. $A(t)=2t(4+5t)$.

  2. $B(t)=(2-3t)(5-4t)$.

Code de déblocage de la correction :

Quels que soient les réels $a$ et $b$, on a :

Développer les expressions suivantes :

  1. $A(t)=(3+t)^2$.

  2. $B(t)=(5-2t)^2$.

Code de déblocage de la correction :

Xcas est un logiciel libre permettant de représenter des fonctions, surtout de faire du calcul littéral et de programmer.
Nous nous en servirons les deux années de BTS pour effectuer des calculs littéraux et obtenir des transformées.
Il peut être légalement et gratuitement télécharger à cette adresse.

Le logiciel Xcas permet de développer des expressions.
Pour cela, il suffit d'utiliser la commande developper(...) (ou la version anglaise expand(...)).

Reprendre les expressions des deux exercices précédents et vérifier les développements obtenus à la main.

En cas de différence entre le résultat obtenu à la main et celui sur ordinateur :

  1. Commencer par vérifier la saisie effectuée sur ordinateur,

  2. Vérifier le calcul effectué à la main,

  3. M'appeler pour vérifier les calculs.

Pour déterminer le produit de deux entiers strictement compris entre 5 et 10 (de la forme $5+x$ et $5+y$ avec $x$ et $y$ strictement compris entre 0 et 5) on se livrait naguère (parfois) au jeu de doigts suivant :

  1. On levait $x$ doigts d'une main et $y$ de l'autre,

  2. On repliait les autres doigts en paumes,

  3. On comptait les doigts levés, on multipliait par 10 et on ajoutait le produit des nombres de doigts repliés dans chaque paume.

Par exemple, pour déterminer le produit des nombres 7 et 8 (que l'on peut mettre sous la forme 5+2 et 5+3), on disposait les doigts de la main comme ceci :

  1. Développer $(5+x)(5+y)$ puis $10(x+y)+(5−x)(5−y)$.

  2. Prouver que cette méthode est correcte.

  3. Quelle manipulation de doigts feriez-vous pour illustrer les produits 6 fois 6, 8 fois 7, 9 fois 5 et 9 fois 9 ?

Développer les expressions suivantes :

  1. $A(t)=4(2-3t)-(4+5t)(3-t)$.

  2. $B(t)=(3t-2)^2-2t(3t-2)$.

  3. $C(t)=(3+t)^2-(2t-5)^2$.

Cliquer pour afficher la solution

  1. Utiliser des flèches pour le développement et penser, au niveau du second terme, à mettre des parenthèses et y mettre l'ensemble du développement du produit.

    $A(t)=4(2-3t)-(4+5t)(3-t)$
    $=4\times2+4\times (-3t)-(4\times 3+4\times (-t)+5t\times 3+5t\times (-t)) $
    $=8-12t-(12-4t+15t-5t^2)$
    $=8-12t-(12+11t-5t^2)$
    $=8-12t-12-11t+5t^2$
    $=-4-23t+5t^2$.

  2. Utiliser soit l'identité remarquable avec $(a-b)^2$, soit écrire le carré $(3t-2)^2$ comme un produit $(3t-2)\times(3t-2)$.
    Pour le développement du second terme, utiliser des parenthèses et y mettre l'ensemble du développement du produit.

    $B(t)=(3t-2)^2-2t(3t-2)$
    $=(3t)^2-2\times 3t \times 2+2^2-(2t\times 3t+2t\times (-2))$
    $=9t^2-12t+4-(6t^2-4t)$
    $=9t^2-12t+4-6t^2+4t$ $=3t^2-8t+4$.

  3. Utiliser soit l'identité remarquable avec $(a+b)^2$, soit écrire le carré $(3+t)^2$ comme un produit $(3+t)\times(3+t)$.
    Pour le développement du second terme, utiliser des parenthèses et y mettre l'ensemble du développement de l'identité remarquable.

    $C(t)=(3+t)^2-(2t-5)^2$
    $=(3)^2+2\times 3 \times t+t^2-((2t)^2-2\times 2t\times 5+5^2)$
    $=9+6t+t^2-(4t^2-20t+25)$
    $=9+6t+t^2-4t^2+20t-25)$
    $=-3t^2+26t-16$.

Vous pouvez trouver d'autres exercices liés au développement d'identités remarquables à cette adresse du site.
Penser à vérifier le résultat obtenu grâce à Xcas ou en cliquant sur le texte appropriée pour afficher le résultat correct.

Voici un test de deux questions portant sur le développement.
Effectuer les développements à la main, quitte à vérifier sur Xcas, puis cocher la bonne réponse à chaque question parmi celles proposées.

Simplifier une expression

Simplifier à la main les expressions suivantes :

  1. $3t(t+2)+5t^3+(1-t)^2$ (développer puis réduire les coefficients des termes de même degré)

    S'aider si besoin de la partie précédente sur le développement d'expressions.

  2. $\sqrt{8}+9\sqrt{2}-5\sqrt{32}$ (décomposer les nombres sous la racine sous forme d'un produit de deux nombres dont un carré si possible)

    Pour tout nombres réels $a$ et $b$ positifs, on peut écrire : $\sqrt{a\color{red}{\times} b}=\sqrt{a}\color{red}{\times}\sqrt{b}$.

  3. $2+\dfrac{3}{t+1}$ (commencer par mettre les deux fractions au même dénominateur)

    On peut remarquer que : $2=\dfrac{2}{1}$.

    Pour tout nombres réels $a$, $b$, $c$ et $d$, avec $b$ et $d$ non nuls, on peut écrire : $\dfrac{a}{b}+\dfrac{c}{d} =\dfrac{a\color{red}{\times d}}{b\color{red}{\times d}} +\dfrac{c\color{blue}{ \times b}}{d\color{blue}{\times b}}$.
    $b\times d$ est un dénominateur commun aux deux fractions.

Code de déblocage de la correction :

Sur Xcas, la commande pour simplifier est simplifier(...) (ou la version anglophone simplify(...)).

Reprendre les expressions de l'exercice précédent et les simplifier à l'aide de Xcas.
Vérifier la cohérence avec les résultats précédemment obtenus à la main.

  • Pour écrire sur Xcas la racine carrée de 2 ($\sqrt{2}$ en notation mathématique), il suffit d'y écrire sqrt(2),

  • Pour écrire une fraction sur Xcas, penser à utiliser des parenthèses avant et après l'opérateur /.

Factoriser une expression

Pour factoriser à la main une expression, il suffit :

  1. soit de trouver un facteur commun à chaque terme de l'expression,

  2. soit de repérer l'expression comme le développement d'une identité remarquable.

Pour factoriser en trouvant un facteur commun, il suffit de souligner le facteur commun de l'expression puis de mettre entre crochets (ou grandes parenthèses si vous préférez) les éléments non soulignés.
Attention à penser à écrire une puissance comme un produit afin de mieux visualiser les éléments à laisser dans le crochet.

Factoriser l'expression suivante : $A(t)=(3t-3)\times(2t+1)-3t\times (2t+1)^2$.
$$\displaystyle{\begin{align}A(t)&=(3t-3)\times(2t+1)-3t\times \color{red}{(2t+1)^2}\\[3pt] &=(3t-3)\times(2t+1)-3t\times \color{red}{(2t+1)\times (2t+1)}\\[3pt] &=\boldsymbol{(3t-3)\times\underline{(2t+1)}-3t\times \underline{(2t+1)}\times (2t+1) }\\[3pt] &=\boldsymbol{\underline{(2t+1)}\times\left[(3t-3)-3t \times (2t+1)\right]}\\[3pt] &=(2t+1)\times\left[(3t-3)-(3t \times 2t+3t\times 1)\right]&& \text{(développement en n'oubliant pas les parenthèses)}\\[3pt] &=(2t+1)\times\left[(3t-3)-(6t^2+3t)\right]\\[3pt] &=(2t+1)\times\left[(3t-3)-6t^2-3t\right]\\[3pt] &=(2t+1)\times\left[-3-6t^2\right]&& \text{(simplification des crochets)}\\[3pt]\end{align}}$$ On peut encore factoriser l'expression dans les crochets ici : $$\displaystyle{\begin{align}A(t)&=(3t-3)\times(2t+1)-3t\times (2t+1)^2\\[3pt] &=(2t+1)\times\left[-3-6t^2\right]\\[3pt] &=(2t+1)\times\left[-3-3\times 2\times t^2\right]&& \text{(remarquer que $6=3\times 2$ pour faire un facteur commun)}\\[3pt] &=(2t+1)\times\left[-\underline{3}\times 1-\underline{3}\times 2\times t^2\right]&& \text{(penser à faire appraître le facteur $\times 1$ lorsque le facteur commun est tout un terme)}\\[3pt] &=(2t+1)\times\underline{3}\left[-1-2\times t^2\right]\\[3pt] &=3(2t+1)\times\left(-1-2t^2\right)\\[3pt] &=3(2t+1)(\color{red}{-}1\color{red}{-}2t^2)\\[3pt] &=\color{red}{-}3(2t+1)(\color{red}{ }1\color{red}{+}2t^2)\\[3pt] \end{align}}$$

Pour factoriser une expression comme le développement d'une identité remarquable, il suffit de compter le nombre de termes puis de donner une expression à $a$ et à $b$, enfin d'utiliser l'identité remarquable sous forme factorisée.

Factoriser $25-4(3x-2)^2$.

1. L'expression $25-4(3x-2)^2$ contient deux termes ($25$ et $4(3x-2)^2$).
Seul le développement $a^2-b^2$ est possible pour que l'expression soit le développement d'une identité remarquable.

2. On identifie :
$25$ doit correspondre à $a^2$ : posons $\color{red}{a=5}$.
$4(3x-2)^2$ doit correspondre à $b^2$ : posons $\color{blue}{b=2(3x-2)}$.

3. Comme $a^2-b^2=(a-b)(a+b)$, $25-4(3x-2)^2=\color{red}{5}^2-(\color{blue}{2(3x-2)})^2$ $=(\color{red}{5}-(\color{blue}{2(3x-2)})(\color{red}{5}+(\color{blue}{2(3x-2)})$ $=(5-6x+4)(5+6x-4)=(9-6x)(1+6x)$.
On peut ici encore factoriser par $3$ le premier facteur : $25-4(3x-2)^2=3(3-2x)(1+6x)$.

Factoriser $36+25t^2-60t$.

1. L'expression $36+25t^2-60t$ contient trois termes ($36$, $25t^2$ et $60t$) et un signe $-$.
Seul le développement $a^2-2ab+b^2$ est possible pour que l'expression soit le développement d'une identité remarquable.

2. On identifie :
$36$ doit correspondre à $a^2$ : posons $\color{red}{a=6}$.
$25t^2$ doit correspondre à $b^2$ : posons $\color{blue}{b=5t}$.

Attention à vérifier que le troisièmeterme correspond bien à $-2ab$ !
Ici, $-2ab=-2\times \color{red}{6}\times \color{blue}{5t}=-60t$. C'est bien l'expression du troisième terme.

3. Comme $a^2-2ab+b^2=(a-b)^2$, $36+25t^2-60t=36-60t+25t^2=\color{red}{6}^2-2\times \color{red}{6}\times \color{blue}{5t}+(\color{blue}{5t})^2$ $=(\color{red}{6}-(\color{blue}{5t}))^2$ $=(6-5t)^2$.

Factoriser à la main les expressions suivantes :

  1. $3t(t+2)+5t^3-t$
  2. $(2t+1)^2-(3+t)^2$

Code de déblocage de la correction :

Sur Xcas, la commande pour factoriser est factoriser() (ou la version anglophone factor(...)).

Par exemple, factoriser(36+25t^2-60t) renvoie $(5*t-6)^2$, expression égale à celle trouvée lors de l'exemple 3 ci-dessus car $(5*t-6)^2=(6-5t)^2$ puisque $(-1)^2=1$.

Reprendre les expressions de l'exercice précédent et les factoriser à l'aide de Xcas.
Vérifier la cohérence avec les résultats précédemment obtenus à la main.

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=36-9(t-4)^2$.

  1. Déterminer la forme développée de $f(t)$.

  2. Déterminer la forme factorisée de $f(t)$.

Code de déblocage de la correction :

Factoriser les expressions suivantes :

  1. $A(t)=1+9t^2+6t$.

  2. $B(t)=(3t-2)^2-2t(3t-2)$.

  3. $C(t)=(3+t)^2-(2t-5)^2$.

Cliquer pour afficher la solution

  1. Pas de facteur commun ici.
    L'expression $A(t)=1+9t^2+6t$ contient 3 termes et aucun signe $-$ : la seule identité remarquable utilisable est $a^2+2ab+b^2=(a+b)^2$.

    Ici, $a=1$ (puisque $a^2$ peut être identifié à 1) et $b=3t$ (car $b^2$ peut être identifé à $9t^2$).

    Vérifions le double produit : $2ab=2\times 1\times 3t=6t$ : c'est bien le dernier terme.

    Ainsi, $A(t)=1+9t^2+6t=(1+3t)^2$.

  2. $3t-2$ est un facteur commun de $B(t)=(3t-2)^2-2t(3t-2)$.

    $B(t)=(3t-2)^2-2t(3t-2)=\underline{(3t-2)}\times (3t-2)-2t\underline{(3t-2)}$ $=\underline{(3t-2)}\times\left[(3t-2)-2t\right]=(3t-2)[t-2]$.
    Ainsi, $(3t-2)^2-2t(3t-2)$ se factorise en $(3t-2)(t-2)$.

  3. Pas de facteur commun ici.
    L'expression $C(t)=(3+t)^2-(2t-5)^2$ contient 2 termes : la seule identité remarquable utilisable est $a^2-b^2=(a-b)(a+b)$.

    Ici, $a=3+t$ (puisque $a^2$ peut être identifié à $(3+t)^2$) et $b=2t-5$ (car $b^2$ peut être identifé à $(2t-5)^2$).

    $C(t)=(3+t)^2-(2t-5)^2$ $=((3+t)-(2t-5))((3+t)+(2t-5))$ $=(3+t-2t+10)(3+t+2t-10)=(13-t)(3t-7)$.

Voici un test de trois questions portant sur la factorisation.
Effectuer les factorisations à la main, quitte à vérifier sur Xcas.

Résoudre une équation

Résoudre une équation du premier degré

Pour résoudre une équation du second degré, il suffit d'isoler l'inconnue $t$ (ou $x$) en utilisant les "opérations inverses" :

Énoncé : Résoudre l'équation $4t+3=0$.

Correction possible :

$$\displaystyle{\begin{align} 4t\color{blue}{+3} &=0 && \color{blue}{\text{une addition par 3 ...}}\\[3pt] 4t &=\color{blue}{-3} && \color{blue}{\text{... est effacée par une soustraction par 3.}}\\[3pt] \color{blue}{4\times}t &=-3 && \color{blue}{\text{une multiplication par 4 ...}}\\[3pt] t &=\frac{-3}{\color{blue}{4}} && \color{blue}{\textrm{... est effacée par une division par 4.}} \end{align}}$$

Conclure la résolution d'une équation en donnant l'ensemble des solutions, notée par convention $S$.

Dans l'exemple précédent, il vous suffit d'écrire à la fin de la résolution de $4t+3=0$ :

$$S=\left\{ -\frac{3}{4} \right\}$$

Si vous voulez trouver cet exemple davantage détaillé de cette méthode, vous pouvez consulter cette page du site, au niveau de l'exemple 5 en particulier.
Une vidéo explicative y est aussi présente.

Résoudre à la main les équations suivantes :

  1. $1-3t=0$

  2. $2t=0$

  3. $3t+4=5t-6$

Code de déblocage de la correction :

Sur Xcas, la commande pour résoudre une équation resoudre(equation,inconnue) (ou la version anglaise solve(equation,inconnue)).

Pour résoudre l'équation $2t-6=8$, il suffit de saisir sur Xcas solve(2*t-6=8,t).

Pour obtenir une valeur approchée d'un nombre réel, il suffit d'utiliser sur Xcas l'instruction evalf.

evalf(sqrt(2)) permet d'obtenir la valeur approchée suivante de $\sqrt{2}$ : 1.41421356237.

Reprendre les équations de l'exercice précédent et vérifier sur Xcas les solutions trouvées.

Pour convertir une température $C$ exprimée en degré Celsius en une température $F$ exprimée en degré Fahrenheit, il suffit d'utiliser la formule suivante : $F=\dfrac{9}{5}\times C +32$.

  1. Déterminer la température en degré Celsius d'un objet ayant une température de 100 degrés Fahrenheit.

  2. Déterminer la température en degré Fahrenheit d'un objet ayant une température de 200 degrés Celsius.

Code de déblocage de la correction :

Vous pouvez trouver d'autres exercices (ainsi que des explications) liés à la résolution d'équations du premier degré à cette adresse du site.
Penser à vérifier le résultat obtenu grâce à Xcas ou en cliquant sur le texte appropriée pour afficher le résultat correct.

Voici un test de trois questions portant sur la résolution d'équations du premier ordre.
Effectuer les résolutions à la main, quitte à vérifier sur Xcas.

Résoudre une équation du second degré

Soit $at^2+bt+c=0$ une équation du second degré (ici, $a\neq 0$).

Pour résoudre à la main cette équation, il suffit de :

  1. calculer d'abord le discriminant $\Delta=b^2-4ac$.

  2. de conclure en fonction du signe de ce discriminant :

    • Si $\Delta>0$, l'équation admet deux solutions réelles distinctes : $t_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $t_2=\dfrac{-b+\sqrt{\Delta}}{2a}$,

    • Si $\Delta=0$, l'équation admet une seule solution réelle (dite double) : $t_0=\dfrac{-b}{2a}$,

    • Si $\Delta\lt0$, l'équation admet aucune solution réelle.

Transposer tous les termes dans le même membre, puis repérer les valeurs des coefficients $a$, $b$ et $c$, ensuite calculer $\Delta$, enfin appliquer la formule correspondante.
Conclure en donnant l'ensemble des solutions.

Énoncé : résoudre l'équation $t^2=3t-2$.

Correction possible :
$t^2=3t-2\iff t^2-3t+2=0$.
Ici, $a=1$, $b=-3$ et $c=2$.
$\Delta=b^2-4ac=(-3)^2-4\times 1\times 2=9-8=1$.
Comme $\Delta>0$, l'équation admet deux solutions réelles distinctes : $t_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-(-3)-\sqrt{1}}{2\times 1}=\dfrac{2}{2}=1$ et $t_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-(-3)+\sqrt{1}}{2\times 1}=\dfrac{4}{2}=2$.
$S=\{1;2\}$

Résoudre les équations suivantes à la main :

  1. $2t^2-5t-3=0$.

  2. $3t^2+t-5=2t^2+t-1$ avec $t\in[-1;6]$.

  3. $t-6-2t^2=0$.

  4. $4t^2+1=4t$.

  5. $t=t^2+1$.

Code de déblocage de la correction :

Reprendre les équations de l'exercice précédent et vérifier sur Xcas les solutions trouvées.

  • Sur Xcas, la commande pour résoudre une équation sur un intervalle est resoudre(equation,inconnue,intervalle) (ou la version anglaise solve(equation,inconnue,intervalle)).

    Pour résoudre l'équation $2t-6=8$ sur $[2;9]$, il suffit de saisir sur Xcas solve(2*t-6=8,t,2..9).

  • Quand xcas renvoie 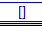factcela signifie que l'équation n'a pas de solution.

Sur une Peugeot 406 1.6i, la résistance $R$ (en Ohms) de la sonde de "température d'eau" en fonction de la température $T$ (en °C) du liquide dans le circuit de refroidissement est donnée par $R(T)=0.58T^2-116T+6000$.

  1. Quelle est la température possible dans le circuit de refroidissement si la résistance est de 1000 Ohms ?

  2. Quelle est la résistance en Ohm de la sonde lorsque la température est de 120 °C.

  3. On veut qu'en fonctionnement, la température du circuit de refroidissement soit comprise entre 0°C et 200°C.
    Quelle est la valeur limite en Ohm de la résistance de la sonde qui doit conduire à l'affichage du message d'alerte selon lequel la température du liquide de refroidissement est trop élevée.

Code de déblocage de la correction :

Un projectile est envoyé au temps $t=0$.
On admet que la hauteur $h$ de ce projectile à l'instant $t$ est donné par $h=-10t^2+129t+67$

  1. À quel instant le projectile touchera-t-il le sol ?

  2. Quelle est la hauteur du promontoire à partir duquel le projectile est envoyé ?

  3. Le projectile peut-il atteindre la hauteur de 498 mètres ? Si oui, à quel(s) moment(s) ?

  4. Le projectile peut-il atteindre la hauteur de 285 mètres ? Si oui, à quel(s) moment(s) ?

Code de déblocage de la correction :

Un projectile est lancé en l'air. Sa hauteur $h$ en fonction du temps $t$ écoulé en seconde depuis le lancement est donné par la relation $h=-5t^2+\dfrac{999}{10}t+2$.

  1. Depuis quelle hauteur est lancé le projectile ?

  2. Le projectile peut-il atteindre l'altitude de 1000 mètres de haut ? Si oui, à quel(s) moment(s) ?

  3. Le projectile peut-il atteindre l'altitude de 501 mètres de haut ? Si oui, à quel(s) moment(s) ?

  4. À quel moment le projectile retombe-t-il au sol ?

Cliquer pour afficher la solution

$h=-5t^2+\dfrac{999}{10}t+2$

Pour chacune des questions, il faut regarger si elle nous indique une valeur du temps et nous demande de trouver une hauteur ou l'inverse.
Il faut conclure au problème concret par une phrase répondant clairement à la question posée.

  1. Depuis quelle hauteur est lancé le projectile ?
    On cherche ici une hauteur, celle hauteur initiale, l'énoncé donne donc ici la valeur du temps : ici $t=0$.
    Il suffit ici de calculer $h$ quand $t=0$. $h=-5\times 0^2+\dfrac{999}{10}\times 0+2=0$. Le projectile est lancé depuis une hauteur de deux mètres.

  2. Le projectile peut-il atteindre l'altitude de 1000 mètres de haut ? Si oui, à quel(s) moment(s) ?
    On connaît ici la hateur : $h=1000$, on cherche le moment $t$ tel que $h=-5t^2+\dfrac{999}{10}t+2$.
    Il suffit ici de résoudre $1000=-5t^2+\dfrac{999}{10}t+2$.
    Sur Xcas, la saisie solve(1000=-5t^2+999/10*t+2,t) renvoie [] : aucune solution réelle à cette équation.
    À la main : $1000=-5t^2+\dfrac{999}{10}t+2\iff 0=-5t^2+\dfrac{999}{10}t-998$.
    Le calcul du déterminant conduit à cette même conclusion : $\Delta=\left(\dfrac{999}{10}\right)^2-4\times (-5)\times (-998)=-9979.99\lt 0$.
    Le projectile n'atteindra jamais la hauteur de 1000 mètres.

  3. Le projectile peut-il atteindre l'altitude de 501 mètres de haut ? Si oui, à quel(s) moment(s) ?
    On connaît ici la hateur : $h=501$, on cherche le moment $t$ tel que $h=-5t^2+\dfrac{999}{10}t+2$.
    Il suffit ici de résoudre $501=-5t^2+\dfrac{999}{10}t+2$.
    Sur Xcas, la saisie solve(501=-5t^2+999/10*t+2,t) renvoie [499/50,10] : deux solutions réelles à cette équation.
    À la main : $501=-5t^2+\dfrac{999}{10}t+2\iff 0=-5t^2+\dfrac{999}{10}t-499$.
    Le calcul du déterminant conduit à cette même conclusion : $\Delta=\left(\dfrac{999}{10}\right)^2-4\times (-5)\times (-499)=\dfrac{1}{100}\gt 0$. Deux solutions possibles :
    $t_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\dfrac{999}{10}-\dfrac{1}{10}}{-10}=10$ et $t_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\dfrac{999}{10}+\dfrac{1}{10}}{-10}=\dfrac{499}{50}=9.98$.
    Le projectile atteindra la hauteur de 501 mètres au bout de 9.98 secondes et de 10 secondes après le lancer.

  4. À quel moment le projectile retombe-t-il au sol ?
    On connaît ici la hateur : $h=0$, on cherche le moment $t$ tel que $h=-5t^2+\dfrac{999}{10}t+2$.
    Il suffit ici de résoudre $0=-5t^2+\dfrac{999}{10}t+2$.
    Sur Xcas, la saisie solve(0=-5t^2+999/10*t+2,t) renvoie [-1/50,20] : deux solutions possibles à cette équation.
    À la main : $0=-5t^2+\dfrac{999}{10}t+2$ :.
    Le calcul du déterminant conduit à cette même conclusion : $\Delta=\left(\dfrac{999}{10}\right)^2-4\times (-5)\times (2)=\dfrac{1002001}{100}=\left(\dfrac{1001}{10}\right)^2 \gt 0$. Deux solutions possibles :
    $t_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\dfrac{999}{10}-\dfrac{1001}{10}}{-10}=20$ et $t_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\dfrac{999}{10}+\dfrac{1001}{10}}{-10}=-\dfrac{1}{50}=-0.02$.
    Attention ! Mathématiquement, il y a deux solutions possibles. Par contre, d'un point de vue concret, le temps $t$ est forcément positif : la solution négative n'ayant pas de sens est à exclure :
    Le projectile retombera au sol au bout de 20 secondes après le lancer.

Résoudre un système

Sur Xcas, on peut résoudre un système en utilisant l'instruction solve([equation1,equation2,...],[inconue1,inconue2,...]).

Pour résoudre le système $\left\{\begin{array}{l l} 2x+3y &= -2\\ x-y &= 9 \end{array}\right.$, il suffit de saisir sur Xcas solve([2x+3y=-2,x-y=9],[x,y]).
L'affichage obtenu [5,-4] signifie que le système admet un unique couple de solution : $(5,-4)$, c'est-à-dire avec $x=5$ et $y=-4$.

Résoudre, grâce à Xcas, le système $\left\{\begin{array}{l l} 3x+5y &= -1\\ 2x+y &= 4 \end{array}\right.$

Code de déblocage de la correction :

Pour consommer moins d'eau, il est recommandé de privilégier des douches aux bains.

Avec 14 douches et 21 bains par semaine, une famille consomme en moyenne 4655 litres d'eau.

Avec 28 douches et 7 bains, cette famille ne consomme plus en moyenne que 3185 litres d'eau.

  1. Sachant que chaque membre de la famille prend chaque jour soit une douche, soit un bain, combien y-a-t'il de personnes de cette famille ?

  2. Déterminer la quantité moyenne d'eau consommée lors d'une douche ? D'un bain ?

Code de déblocage de la correction :

Soit $f$ la fonction définie par $f(t)=at^2+bt+c$ dont la parabole est tracée ci-dessous.

  1. Traduire par des relations entre les inconnues $a$, $b$ et $c$ le fait que :

    1. La courbe passe le point $A$ de coordonnées $(0;2)$ du repère.

    2. Elle a pour sommet le point $S(3;5)$.

    3. Elle passe par le point $B$ le symétrique du point $A$ par rapport à l’axe de symétrie de la parabole.

  2. En déduire que les inconnues $a$, $b$ et $c$ sont solutions d'un système à exhiber.

  3. Déterminer les réels $a$, $b$ et $c$ en résolvant le système $\left\{\begin{array}{r l} c &= 2\\ 9a+3b+c &= 5\\ 36a+6b+c &=2 \end{array}\right.$.

Code de déblocage de la correction :

Un joueur de tennis, sur sa ligne de fond de cours, lobe son adversaire Tommy se trouvant au filet.
On admet que la trajectoire de la balle est une parabole d'équation $y=ax^2+bx+c$.
On admet que la balle est frappée au dessus de la ligne de fond de cours à une hauteur de 2m, que sa trajectoire est parallèle aux lignes de couloir et qu'elle atteint sa hauteur maximale de 4 mètres à 10 mètres de la ligne de fond de cours. Un terrain de tennis a pour longueur 23.77m.
Sachant que l'adversaire est lobé, la balle retombe-t-elle dans le terrain ?

Code de déblocage de la correction :

Dans une bibliothèque familiale, un rayon comporte 32 livres et bandes dessinées.

La fille de cette famille remarque que si elle enlève de ce rayon 5 livres et 3 bandes dessinées alors il y a deux fois plus de bandes dessinées que de livres.

Combien de bandes dessinées comporte le rayon de la bibliothèque ?

Code de déblocage de la correction :

Un magasin vend des coques de téléphones et des stylos.
Le mois dernier, la recette pour la vente de 350 coques et 700 stylos a été de 4900€.

Le vendeur réalise un bénéfice de 60% du prix du stylo et de 40% du prix d'une coque.
Le mois dernier, le vendeur a réalisé un bénéfice de 2380€.

Quel est le prix d'une coque de téléphone dans ce magasin ?

Code de déblocage de la correction :

Un livreur dépose à un magasin de primeurs 50 caisses de fruits.
Le total des caisses pèse 474 kg.

Chaque caisse ne contient soit que des pommes, soit que du raisin.

Sachant qu'une caisse de pommes pèse 12kg tandis qu'une caisse de raisin pèse 7.5 kg, déterminer le nombre de caisses de pommes et de raisins déposées par le livreur.

Cliquer pour afficher la solution

Comme il y a deux valeurs que l'on cherche dans ce problème, utilisons deux inconnues :

Comme il y a en tout 50 caisses, on déduit la relation : $x+y=50$.

De plus, chaque caisse de pommes pèse 12kg. Comme il y a en $y$, la masse de toutes les caisses de pommes est $12y$.
De même, chaque caisse de raisins pèse 7.5kg. Comme il y a en $x$, la masse de toutes les caisses de pommes est $7.5x$.
Ainsi, la masse totale de toutes les caisses est de $7.5x+12y$.
Comme cette masse vaut aussi 474, on en déduit que : $7.5x+12y=474$.

Le problème concret revient donc à résoudre $\left\{ \begin{array}{r c r} x+y &= &50 \\\ 7.5x+12y &= & 474 \end{array} \right.$

Pour l'instruction solve([x+y=50,7.5*x+12*y=474],[x,y]), Xcas renvoie [28.0,22.0].

Ainsi, $x=28$ et $y=22$.
Finalement, le livreur a déposé 28 caisses de raisins et 22 de pommes.

Voici un test de deux questions portant sur les systèmes.
Modéliser le problème donné puis résoudre grâce à Xcas le système correct pour répondre concrètement au problème concret.

Représentation graphique sur Geogebra

Geogebra est un logiciel libre permettant de représenter des fonctions, de faire de la géométrie, de travailler sur tableur, de faire du calcul littéral et de programmer.
Nous nous en servirons les deux années de BTS surtout pour les représentations graphiques et les probabilités.
Il peut être légalement et gratuitement téléchargé à cette adresse.

On considère la fonction $f$ définie par $f(t)=4t^2+5t+1$.

    1. Résoudre à la main l'équation $f(t)=0$.

    2. Vérifier sur Xcas la résolution de l'équation $f(t)=0$.

  2. Tracer la courbe représentative de $f$ sur Geogebra pour vérifier les réponses obtenues.

    Il est préférable de saisir $x$ comme variable sur Geogebra.

  3. Grâce au graphique et aux questions précédentes, en déduire les solutions de l'inéquation $f(t)>0$.

Code de déblocage de la correction :

On considère les fonctions $f:t\mapsto 5t^2+2t$ et $g:t\mapsto- 12 t+ 52$.

  1. Résoudre à la main l'équation $f(t)=g(t)$.

  2. Utiliser Xcas pour vérifier le résultat précédent.

    1. Représenter les fonctions $f$ et $g$ sur Geogebra.

    2. Utiliser Geogebra pour vérifier le résultat de la résolution de l'équation.

Code de déblocage de la correction :

Dans un laboratoire, un observateur étudie l'évaporation de deux liquides A et B en notant chaque jour la hauteur des liquides dans leurs tubes respectifs. Il déduit de ces relevés que les hauteurs $h_A(t)$ et $h_B(t)$ en cm, s'expriment en fonction du temps $t$, en jours, par les formules $h_A(t)=-0.2t+8$ et $h_B(t)=-1.3 t+9$.

  1. Quelle était la hauteur de chaque liquide au départ de l'observation ?

  2. Au bout de combien de temps, il n'y a plus de liquide dans le tube A ? Dans le tube B ?

    1. Tracer sur Geogebra les courbes représentant les fonctions $h_A$ et $h_B$.

    2. Déterminer l'instant où les deux tubes ont la même hauteur de liquide.

  4. Quel est le tube dont la hauteur de liquide décroît le plus rapidement ?

Code de déblocage de la correction :

Demander le programme !

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲