Intérêt
Les matrices facilitent la résolution de système ; elles permettent aussi de résoudre par des modélisations informatiques
des équations dont on ne connaît de solutions exactes.
Elles serviront aussi lorsque l'on étudiera l'évolution de processus aléatoires.
Notion de matrice
Vous êtes installateur de matériel informatique.
Un de vos fournisseurs de matériel informatique commercialise trois composants notés $S$, $N$ et $R$, chacun existant en deux
versions "classique" et "premium".
Les tarifs de ces fournisseurs sont donnés dans tableau suivant :

Ce tableau comporte :
-
une première ligne et une colonne de gauche qui précisent la nature des "entrées" : le type de composant et la version.
-
un tableau de nombres de 2 lignes et 3 colonnes qui donnent les "sorties" : le montant de la facturation.
Le tableau de ces $2\times 3=6$ nombres, sans unités, est appelé une matrice et se note : $A= \begin{pmatrix} 35&65&90 \\ 60&110&150 \end{pmatrix}$.
Plus généralement :
On appelle matrice $n\times p$ tout tableau de nombres, réels ou complexes, ayant $n$ lignes et $p$ colonnes.
On dit que la matrice est carrée si $n=p$. On parle de matrice d'ordre $n$
On note $A=(a_{ij})_{1\leq i \leq n \textrm{ et } 1\leq j \leq p }$ la matrice : $A= \begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1j}&\ldots&a_{1p}\\ a_{21}&a_{22}&\ldots&a_{2j}&\ldots&a_{2p}\\ \vdots&&&\vdots&&\vdots\\ a_{i1}&\vdots&\vdots&a_{ij}&\ldots&a_{ip}\\ \vdots&&&\vdots&&\vdots\\ a_{n1}&a_{n2}&\ldots&a_{nj}&\ldots&a_{np}\\ \end{pmatrix}$, où $a_{ij}$ se situe à la ligne $i$ et à la ligne $j$.
$a_{ij}$ est appelé le terme général de la matrice $A$.
On dit que la matrice est carrée lorsque $n=p$, c'est-à-dire lorsque le tableau possède autant
de lignes que de colonnes.
On parle alors de matrice d'ordre $n$.
Une usine fabrique trois sortes d’articles : $a_1$, $a_2$ et $a_3$ à partir de trois modules : $m_1$, $m_2$ et $m_3$.
On donne le nombre de modules de chaque type nécessaire pour fabriquer chaque sorte d'article dans le tableau suivant.
|
Articles |
||||
| $a1$ | $a2$ | $a3$ | ||
| Modules | $m1$ | 3 | 9 | 5 |
| $m2$ | 4 | 0 | 9 | |
| $m3$ | 4 | 8 | 6 | |
-
Déterminer la matrice associée à ce tableau.
-
Que pouvez-vous dire de cette matrice ?
Opérations sur les matrices
Égalité
Deux matrices $A$ et $B$ sont égales si elles ont :
-
même nombre de lignes $n$,
-
même nombre de colonnes $p$,
-
même coefficient de même indice : $a_{ij}=b_{ij}$.
Addition de deux matrices
Les tarifs de votre fournisseur de matériel informatique sont donnés dans tableau suivant :

On note $A$ la matrice associée à ce tableau.
Ce fournisseur de matériel informatique veut augmenter ses montants de facturation selon le tableau :

On note $B$ la matrice associée à ce tableau.
-
Déterminer les matrices $A$ et $B$.
-
Déterminer la matrice $C$.
Soit $C$ la matrice des nouveaux tarifs appliqués.
Chaque nouveau tarif étant la somme de l’ancien tarif et de son augmentation, on convient de noter $C=A+B$.
Plus généralement :
Soient $A$ et $B$ ayant le même nombre $n$ de lignes et le même nombre $p$ de colonnes.
La matrice somme $C=A+B$ est la matrice ayant $n$ lignes et $p$ colonnes et ayant pour terme général $c_{ij}=a_{ij}+b_{ij}$.
$\begin{pmatrix} 0&1&-5\\ 5&12&3 \end{pmatrix}+\begin{pmatrix} 1&-2&5\\ 3&2&1 \end{pmatrix}=$
Multiplication d'une matrice par un réel
On reprend la matrice $A= \begin{pmatrix} 35&65&90 \\ 60&110&150 \end{pmatrix}$ donnant les tarifs initiaux de votre
fournisseur.
Suite à la disparition d’un fournisseur concurrent et afin d’augmenter les marges et les salaires,
l’entreprise décide d’augmenter tous ses tarifs de 10%.
-
Recopier et compléter la phrase suivante : Augmenter de 10% revient à ...
-
On note $D$ la matrice donnant les nouveaux tarifs.
Comme tous les tarifs sont multipliés par 1.1, on peut noter : $D=1.1\times A$. Déterminer la matrice $D$.
Plus généralement :
Soit $A$ une matrice ayant $n$ lignes et $p$ colonnes et soit $k$ un réel.
La matrice $B=k A$ est la matrice ayant aussi $n$ lignes et $p$ colonnes et ayant pour terme général $b_{ij}=k\times a_{ij}$
Simplifier le calcul suivant : $-2\times\begin{pmatrix} 5&-1 \\ 1&5\\ 3&2 \end{pmatrix}=$
Pour toute matrice $A$, $B$ et $C$ à $n$ lignes et $p$ colonnes et tout réel $k$, et $k'$, on a :
-
$A+B=B+A$
-
$(A+B)+C=A+(B+C)=A+B+C$
-
$(kk')A=k(k'A)=(k'k)A=k'(kA)$
-
$k(A+B)=kA+kB$
-
$(k+k')A=kA+k'A$
Vous pouvez additionner des matrices dans l'ordre que vous voulez :
Vous pouvez multiplier par des réels dans l'ordre que vous voulez :
Vous pouvez distribuer un produit par un réel avec une addition comme habituellement :
Soustraction de deux matrices
Soient $A$ et $B$ deux matrices ayant $n$ lignes et $p$ colonnes.
La matrice différence $C=A-B$ est la matrice $A+(-1)\times B$
$\begin{pmatrix} -2&2 \\ 0&1\\ 5&3 \end{pmatrix}-\begin{pmatrix} 5&-1 \\ 1&5\\ 3&2 \end{pmatrix}=$
Multiplication de deux matrices
Une usine fabrique trois sortes d’articles : $a1$, $a2$ et $a3$ à partir de trois modules : $m1$, $m2$ et $m3$. On donne :
|
Articles |
||||
| $a1$ | $a2$ | $a3$ | ||
| Modules | $m1$ | 3 | 9 | 5 |
| $m2$ | 4 | 0 | 9 | |
| $m3$ | 4 | 8 | 6 | |
| Modules | |||
| $m1$ | $m2$ | $m3$ | |
| 5 | 6 | 3 | Masse unitaire en kilogramme |
| 180 | 250 | 150 | Coûts unitaires en euros |
Explications : pour fabriquer un article $a2$, il faut 9 modules $m1$ et 8 modules $m3$. Un module $m1$ pèse 5kg et coûte 180 euros.
-
Calculer la masse d’un article $a1$ sachant qu’il n’est construit qu’à partir des modules $m1$, $m2$ et $m3$.
-
Calculer les coûts unitaires (en euro) liés aux composants pour fabriquer un article $a1$.
-
Compléter le tableau suivant :
Articles $a1$ $a2$ $a3$ ... ... ... Masse unitaire en kilogramme ... ... ... Coûts unitaires en euros -
-
Le premier tableau de l'exercice, celui qui lie chaque article aux modules nécessaires à sa fabrication est associée à une matrice $B$. Déterminer cette matrice $B$.
-
Le deuxième tableau de l'exercice, celui qui lie chaque module à une masse et un coût est associée à une matrice $A$. Déterminer cette matrice $A$.
-
Le dernier tableau de l'exercice, celui obtenu à la question précédente, est associée à une matrice $C$. Déterminer cette matrice $C$.
-
L’ensemble des opérations faites pour obtenir ce tableau correspondent à ce que l’on appelle la multiplication entre deux matrices.
Ainsi, cette nouvelle matrice est notée $A\times B$ ou simplement $AB$.
On peut visualiser l'ensemble des opérations liées à la multiplication avec le schéma suivant :

Soient $A$ une matrice à $n$ lignes et à $p$ colonnes et $B$ une matrice à $p$ lignes et $q$ colonnes.
Le produit de la matrice $A$ par la matrice $B$ est la matrice $C$, notée $AB$ ou $A\times B$ est défini ainsi :
-
$C$ est une matrice à $n$ lignes et $q$ colonnes,
-
Le terme général de $C$ est défini par $c_{ij}=a_{i1}\times b_{1j}+a_{i2}\times b_{2j}+...+a_{in}\times b_{nj}$ $=\sum\limits_{k=1}^{n}a_{ik}\times b_{kj}$.
Attention ! La multiplication $A\times B$ d'une matrice $A$ par une matrice $B$ n'est possible que si le nombre de colonnes de la matrice $A$ est égal au nombre de lignes de $B$.
Soient $A=\begin{pmatrix} 1&-1&4 \\ 1&5&3\\ 2&3&4 \end{pmatrix}$, $B=\begin{pmatrix} 8&4&-6 \\ 2&3&1\\ 0&-2&-5 \end{pmatrix}$ et $C=AB$.
Démontrer que $c_{32}=9$.
Calculer à la main les produits matriciels suivant :
- $\begin{pmatrix} -2&1&2 \\ 0&1&-5\\ 5&12&3 \end{pmatrix}\times \begin{pmatrix} 5&-1&3 \\ 1&-2&5\\ 3&2&1 \end{pmatrix}$
Pour toute matrice $A$ à $n$ lignes et $p$ colonnes, $B$ et $C$ matrice à $p$ lignes et $q$ colonnes et tout réel $k$, on a :
-
$k(A\times B)=(kA)\times B=A\times (kB)$
-
$A\times (B+C)=A\times B+A\times C$
Pour toute matrice $A$ à $n$ lignes et $p$ colonnes, $B$ matrice à $p$ lignes et $q$ colonnes et $C$ matrice à $q$ lignes et $m$ colonnes, on a :
-
$k(A\times B)\times C=A\times (B\times C)$
Pour toute matrice $A$ et $B$ à $n$ lignes et $p$ colonnes et $C$ matrice à $p$ lignes et $q$ colonnes, on a :
-
$(A+B)\times C=A\times C+B\times C$
On considère les matrices $A=\begin{pmatrix} 1&0 \\ 0&0 \end{pmatrix}$ et $B=\begin{pmatrix} 0&0 \\ 1&0 \end{pmatrix}$.
-
Calculer le produit $A\times B$.
-
Calculer le produit $B\times A$.
-
Que remarquez-vous ?
Attention ! Si un produit $A\times B$ existe le produit $B\times A$ n'existe pas focément.
De plus, même lorsque ces deux produits existent, il se peut que $A\times B \neq B\times A$.
Il est possible avec des matrices d'avoir $A\times B = 0$ avec $A\neq 0$ et $B\neq 0$, contrairement avec des nombres réels ou complexes.
Utilisation de Xcas
-
Une matrice est sasie sur Xcas comme une liste de listes formées des éléments de chaque ligne.
-
Les opérations addition, soustraction et multiplication sont accessibles directement avec
+,-et*.
Pour vérifier les résultats obtenus à l'exercice précédent, il suffit de saisir
les deux matrices puis les opréations voulues :

Matrice unité et matrice inverse
On appelle matrice unité la matrice carrée $I_{n}$ à $n$ lignes et $n$ colonnes telle que $i_{ii}=1$ et $i_{ij}=0$ si $i\ne j$.
$I_n=\begin{pmatrix} 1&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&1 \end{pmatrix}$
- $I_2=\begin{pmatrix} 1&0\\0&1 \end{pmatrix}$
- $I_3=\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1 \end{pmatrix}$
Pour toute matrice carrée $A$ à $n$ lignes et $n$ colonnes, $A\times I_n=I_n\times A=A$
On considère les matrices $A=\begin{pmatrix} 2&-\dfrac{3}{2}\\-1&1\end{pmatrix}$ et $B=\begin{pmatrix} 2&3\\2&4\end{pmatrix}$.
-
À l'aide de Xcas, calculer les produits $A\times B$ et $B\times A$.
-
Que remarquez-vous ?
Soit $A$ une matrice carrée à $n$ lignes et $n$ colonnes.
S'il existe une matrice carrée $B$ à $n$ lignes et $n$ colonnes telle que $AB=BA=I_n$, alors on dit que $A$ est
inversible et $B$ est la matrice inverse de $A$ on la note $A^{-1}$.
Si $A\times B=B\times A=I_n$, alors $B$ est la matrice inverse de $A$ mais $A$ est aussi la matrice inverse de $B$.
On donne $A=\begin{pmatrix} 1&2&-1 \\ 1&0&2\\ -1&2&-1 \end{pmatrix}$ et $B=\frac18\begin{pmatrix} 4&0&-4\\ 1&2&3\\ -2&4&2\\ \end{pmatrix}$
Montrer que $B=A^{-1}$
Pour déterminer à l'aide de Xcas la matrice inverse $A^{-1}$ d'une matrice inversible $A$, il suffit :
-
de saisir la matrice $A$,
-
de saisir ensuite
A^(-1)ou mêmeA^-1.
Pour connaître la matrice inverse de $A=\begin{pmatrix}9&5&5\\3&1&2\\2&2&1\end{pmatrix}$ :

Exemples d’utilisation des matrices
Représentation matricielle d’un système d’équations linéaires
Considérons le système d’équations $(S): \left \{ \begin{array}{c c} ax+by & =x' \\ cx+dy &=y' \\ \end{array} \right.$
On pose :
-
$A$ la matrice carrées des coefficients : $A=\begin{pmatrix} a&b\\c&d\end{pmatrix}$,
-
$X$ la matrice colonnes des inconnues : $X=\begin{pmatrix} x\\y\end{pmatrix}$,
-
$X'$ la matrice colonnes des valeurs des seconds membres : $X'=\begin{pmatrix} x'\\y'\end{pmatrix}$,
Comme $A\times X=\begin{pmatrix} ax+by\\cx+dy\end{pmatrix}$, le système $(S): \left \{ \begin{array}{c c} ax+by & =x' \\ cx+dy &=y' \\ \end{array} \right.$ peut s'écrire à l'aide de matrices : $\begin{pmatrix} a&b\\c&d\end{pmatrix} \times \begin{pmatrix} x\\y\end{pmatrix}= \begin{pmatrix} x'\\y'\end{pmatrix}$, soit $A\times X=X'$.
Une usine fabrique trois sortes de pièces dans un même matériau.
Le nombre total de pièces fabriquées est $N$, leur masse totale en kg est $M$ et le coût total d’expédition en euros est $C$.
On peut synthétiser cette situation par le tableau incomplet suivant :

Le système suivant fournit des informations complémentaires sur cette fabrication :
$(S): \left \{ \begin{array}{r l r l r l} x &+&y&+&z & =N \\ x&+&2y&+&3z &=M \\ 40x&+&20y&+&10z &=C \end{array} \right.$
-
Recopier et compléter le tableau de synthèse ci-dessus à l’aide des coefficients du système.
-
On considère les matrices $V=\begin{pmatrix}x\\y\\z\end{pmatrix}$ et $B=\begin{pmatrix}N\\M\\C\end{pmatrix}$.
Quelle doit être la matrice $A$ pour que le système s’écrive $AV=B$ ? -
Déterminer la matrice inverse de la matrice $A$.
-
Sans effectuer les produits de matrices en cause, démontrer l’équivalence : $AV=B \iff V=A^{-1}B$.
-
Déduire de la question précédente $V$ en fonction de $N$, $M$ et $C$.
-
Dans cette question $C=8100$€, $M=360$kg et $N=250$.
Combien a-t-on fabriqué de pièces de chaque catégorie ?
Modélisation de phénomènes stochastiques
Dans un test sur un nouveau médicament contre l'herpès, les patients examinés ont été divisés en trois groupes :
-
les patients avec le syndrome débutant ($D$),
-
les patients avec le syndrome avancé ($A$),
-
les patients rétablis ($R$).
Les patients sont en nombre constant tout au long du test.
On a pu établir d'une semaine à la suivante que :
-
un patient dans l'état ($D$) a une probabilité de 30% de rester dans l'état ($D$), de 20% de passer à l'état ($A$) et de 50% de passer à l'état ($R$).
-
un patient dans l'état ($A$) a une probabilité de 80% de rester dans l'état ($A$), de 0% de passer à l'état ($D$) et de 20% de passer à l'état ($R$).
-
un patient dans l'état ($R$) ne peut que le rester.
On note $P_n$ la matrice ligne $P_n=\begin{pmatrix}d_n&a_n&r_n\end{pmatrix}$ où $d_n$, $a_n$ et $r_n$ désignent les probabilités qu'un patient
choisi au hasard, soit respectivement dans le groupe ($D$), ($A$) et ($R$) au bout de $n$ semaines.
On suppose qu'au départ du test, 20% des patients ont un syndrome débutant et 80% ont un syndrome avancé.
-
À l'aide de l'énoncé, déterminer la matrice $P_0$.
-
À l'aide de l'énoncé, déterminer la matrice carrée $M$ d'ordre 3 telle que $P_1=P_0\times M$.
Aidez-vous d'un schéma comme le suivant :

-
Calculer la proportion de patients dans chaque au bout d'une semaine.
-
On admet que pour tout entier $n$, on a $P_n=P_0\times M^n$.
À l'aide de l'affichage de Xcas suivant, que pouvez-vous conjecturer quant au comportement à l'infini de la suite $(P_n)$ ?

-
Que peut-on en déduire quant à l'efficacité du médicament ?
Exercices
notation matricielle
Écrire la matrice d'ordre 2 telle que : $a_{11}=3$, $a_{22}=4$, $a_{12}=-1$ et $a_{21}=6$.
Calcul matriciel
L’inventaire des ordinateurs de type A et de type B, en stock dans trois points de vente de la grande chaîne P'tiD'art est donné par la matrice $M=\begin{pmatrix} 8&11 \\ 17&5\\ 12&1 \end{pmatrix}$, où les lignes indiquent les stocks d’ordinateurs disponibles dans chacun des trois points de vente.
Le prix de vente en euros des ordinateurs de type A et B est donné par la matrice à une seule colonne $N=\begin{pmatrix} 300 \\ 500 \end{pmatrix}$.
-
Calculer à la main la matrice $M\times N$.
-
Que représentent concrètement les nombres obtenus dans la matrice $M\times N$ ?
Soient les deux matrices $M_1=\begin{pmatrix} 5&2\\ 7&3 \end{pmatrix}$ et $M_2=\begin{pmatrix} 3&-2\\ -7&5 \end{pmatrix}$.
-
-
Calculer à la main $M_1\times M_2$.
-
Calculer à la main $M_2\times M_1$.
-
Vérifier sur Xcas.
-
-
Que peut-on dire des matrices $M_1$ et $M_2$ ?
Soient les matrices $A=\begin{pmatrix} 2&-1 \\ 3&0\\ \end{pmatrix}$ et $B=\begin{pmatrix} 5&4\\ 1&8\\ \end{pmatrix}$
Calculer $(A+B)^2$ et $A^2+2AB+B^2$.
Comment expliquer ce résultat ?
Pour décrire les mouvements de translation et de rotation dans l’espace des robots utilisés, par exemple, dans l’industrie automobile, on utilise des matrices.
On considère les matrices suivantes, qui correspondent à deux rotations dans l’espace : $A=\begin{pmatrix}1&0&0&0\\0&0&-1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}$ et $B=\begin{pmatrix}0&0&1&0\\0&1&0&0\\-1&0&0&0\\0&0&0&1\end{pmatrix}$.
Calculer la matrice $A\times B$ qui correspond à la composée des deux rotations dans l’espace.
Résolution de systèmes par calcul matriciel
Pour le cross des élèves de premières, un lycée a commandé 120 petites bouteilles d'eau et 180 sachets de biscuits pour la somme de 219,60 euros.
Pour le cross des élèves de terminale, l'établissement a commandé 100 bouteilles d'eau et 190 paquetes de biscuits pour un total de 227,80 euros.
-
Modéliser cette situation sous forme d'un système $(S)$ de deux équations à deux inconnues $x$ et $y$ respectivement au prix d'une bouteille d'eau et à celui d'un paquet de biscuits.
-
Déterminer les matrices $A$, $X$ et $B$ telles que le système $(S)$ s'écrit sous la forme $AX=B$.
-
Déterminer $A^{-1}$ la matrice inverse de $A$.
-
Résoudre l'équation matricielle $AX=B$ puis en déduire la solution du système.
Interpréter la solution concrètement.
Une entreprise fabrique trois types de pièces différentes : $P_1$, $P_2$ et $P_3$.
Un programme de production pour une journée donnée s’exprime par un triplet $(x ; y ; z)$.
Plus précisément, le programme de production $(x ; y ; z)$ correspond à la production de
$x$ pièces de type $P_1$, $y$ pièces de type $P_2$ et $z$ pièces de type $P_3$ au cours d’une journée donnée.
Pour réaliser un programme de production $(x ; y ; z)$, on utilise $a$ kilogrammes d’acier, $b$ kilogrammes de bois
et cela nécessite $t$ heures de travail, ce que l’on résume par le triplet $(a ; b ; t)$.
-
Pour une pièce de type $P_1$, on a besoin de 0.5 kg d’acier, 1 kg de bois et 1 h de travail.
-
Pour une pièce de type $P_2$, on a besoin de 1 kg d’acier, 2 kg de bois et 1 h de travail.
-
Pour une pièce de type $P_3$, on a besoin de 1.5 kg d’acier, 2 kg de bois et 3 h de travail.
-
Justifier que $a=0.5x+y+1,5z$.
-
Exprimer également $b$ et $t$ en fonction de $x$, $y$ et $z$.
-
Justifier que ces expressions peuvent se traduire matriciellement par l’égalité $Y=AX$ dans laquelle $A=\begin{pmatrix}0.5&1&1.5\\1&2&2\\1&1&3\end{pmatrix}$, $X=\begin{pmatrix}x\\y\\z\end{pmatrix}$ et $Y=\begin{pmatrix}a\\b\\t\end{pmatrix}$.
-
Durant une journée, l’entreprise a produit 37 pièces de type $P_1$, 52 de type $P_2$ et 65 de type $P_3$.
-
Écrire la matrice $X$ correspondant à cette journée.
-
Déterminer la quantité d’acier, de bois et le nombre d’heures de travail pour la production de cette journée.
-
-
-
Déterminer à l'aide de Xcas la matrice inverse $A^{-1}$.
-
Utiliser une matrice pour résoudre le système (S) d’inconnues $x$, $y$ et $z$ : (S) $\left \{ \begin{array}{r l r l r l} 0.5x &+&y&+&1.5z & =163 \\ x&+&2y&+&2z &=277 \\ x&+&y&+&3z &=274 \end{array} \right.$.
-
Lors d’une journée de production, 163 kg d’acier et 277 kg de bois ont été utilisés et 274 heures de travail ont été nécessaires.
Quelles quantités de pièces de chaque type $P_1$, $P_2$ et $P_3$ ont été fabriquées dans cette journée ?
-
-
Lors d’une journée de production, 175 kg d’acier et 299 kg de bois ont été utilisés et 275 heures de travail ont été nécessaires.
Quelles quantités de pièces de chaque type $P_1$, $P_2$ et $P_3$ ont été fabriquées cette journée ?
Une agence de voyage propose un circuit touristique pour visiter 3 villes A, B et C. Le client peut choisir la durée de séjour dans chacune des villes. L'agence propose des tarifs qui diffèrent selon la période. Il existe 3 périodes touristiques :
-
une période haute (tarifs plus élevés),
-
une période moyenne,
-
une période basse.
Les prix journaliers, en centaines d'euros par personne, dans les différents lieux sont donnés dans le tableau suivant :
|
Ville A |
Ville B |
Ville C |
|
|---|---|---|---|
|
Période haute |
$2.5$ |
$3.5$ |
$1.5$ |
|
Période moyenne |
$2$ |
$2$ |
$1.5$ |
|
Période basse |
$1$ |
$1$ |
$1$ |
On appelle $P$ la matrice $\begin{pmatrix} 2.5&3.5&1.5\\ 2&2&1.5\\1&1&1 \end{pmatrix}$ qui représente les prix journaliers par ville et par période.
-
Monsieur M choisit un circuit de 14 jours qui comprend 6 jours dans la ville A, 5 jours dans la ville B et 3 jours dans la ville C. On associe la matrice $M=\begin{pmatrix} 6\\ 5\\3 \end{pmatrix}$.
-
Calculer le produit matriciel $P\times M$.
Que représentent les termes de la matrice obtenue ? -
Monsieur M dispose d'un budget de 2600€. À quelle période pourra-t-il faire son voyage ?
-
-
Déterminer la matrice inverse de $P$.
-
Dans une publicité, l'agence de voyage affirme qu'un circuit complet de 14 jours est possible au prix de 2600€ en période haute, 2250€ en période moyenne et 1400€ en période basse.
Comment se compose ce voyage ? -
On considère le système suivant : $\left \{ \begin{array}{r r r r r c} 2.5a &+&3.5b&+&1.5c & =38 \\ 2a &+&2b&+&1.5c & =26 \\ a&+&b&+&c & =14\end{array} \right.$.
-
Réécrire ce système à l'aide d'un produit matriciel faisant apparaître, entre autres la matrice $P$ et celle $X=\begin{pmatrix}a\\b\\c\end{pmatrix}$.
-
Résoudre le système en utilisant l'écriture matricielle.
-
Que représentent par rapport au voyage les termes obtenus comme solutions du système ?
En informatique, on utilise des triplets de nombres réels pour identifier une couleur.
Comme les triplets de couleurs font penser à des coordonnées de points dans l'espace, on parle d'espace colorimétrique.
Dans l'espace RVB (pour Rouge, Vert et Bleu) on associe, par exemple, à la couleur rouge le triplet (1;0;0).
Il est parfois nécessaire d'utiliser un autre espace colorimétrique : l'espace YUV (où Y désigne la luminance et U et V
désignent la chrominance) est, par exemple, utilisé lors de la compression d'images au format JPEG ou vidéo au format MPEG.
La composante Y correspond au niveau de gris tandis que U et V correspondent à la différence entre
ce niveau de gris avec le niveau de bleu puis avec le niveau de rouge.
Pour faire la conversion du RVB vers le YUV, on utilise la
relation matricielle suivante :
$\begin{pmatrix}Y\\U\\V\end{pmatrix}=\begin{pmatrix}0.299&0.587&0.114\\-0.14713&-0.28886&0.436\\0.615&-0.51498&-0.10001 \end{pmatrix} \times \begin{pmatrix}R\\V\\B\end{pmatrix}$.
-
Quel est le triplet qui représente la couleur rouge dans le système YUV ?
-
La couleur "amande" est représentée par le triplet $(0.883 ; -0.041 ; 0.05)$ dans le système YUV.
Déterminer le triplet correspondant à cette couleur dans le système RGB.
Une société produit trois types de fibres optiques à partir de silice, forme naturelle du dioxyde de silicium ($SiO_2$) qui entre dans la composition de nombreux minéraux. Elle produit :
-
$x$ pièces du type A, dont le débit supporté vaut 1 gigabit par seconde.
-
$y$ pièces du type B, dont le débit supporté vaut 10 gigabits par seconde.
-
$z$ pièces du type C, dont le débit supporté vaut 100 gigabits par seconde.
Pour une pièce, la masse de silice utilisée et le temps de production de chacun de ces types de fibres sont récapitulés dans le tableau suivant :
|
Type de fibre |
A |
B |
C |
|---|---|---|---|
|
Masse de silice en kg (par pièce) |
3 |
4 |
7 |
|
Temps de production en h (par pièce) |
2 |
3 |
5 |
La société modélise cette fabrication afin d’envisager différents scénarios sur une période donnée.
Pour cette période, on note $N$ le nombre total de pièces produites,
$S$ la masse totale en kg de silice utilisée et $H$ le temps total de production exprimé en heure.
-
Justifier le fait que $x$, $y$ et $z$ vérifient le système $\left \{ \begin{array}{r l r l r l} x &+&y&+&z & =N \\ 3x&+&4y&+&7z &=S \\ 2x&+&3y&+&5z &=H \end{array} \right.$.
-
On considère les matrices colonnes $X=\begin{pmatrix}x\\y\\z\end{pmatrix}$ et colonnes $Y=\begin{pmatrix}N\\S\\H\end{pmatrix}$.
Déterminer la matrice carrée $M$ qui traduit le système ci-dessus par l'équation matricielle $M\times X=Y$. -
Calculer $Y$ lorsque $X=\begin{pmatrix}20\\10\\30\end{pmatrix}$.
Interpréter les résultats obtenus dans le contexte de l’exercice. -
Pour une période donnée, l’entreprise dispose de 94 kg de silice et de 67 heures de production. Elle souhaite fabriquer 21 pièces de fibres.
Combien de pièces de chaque type peut-elle fabriquer ?
Un constructeur de planches de surf fabrique 3 modèles. La conception de chaque modèle nécessite le passage par 3 postes de travail. Le tableau 1 indique le nombre d’heures nécessaires par modèle et par poste pour réaliser les planches :
|
Tableau 1 |
Poste 1 |
Poste 2 |
Poste 3 |
|---|---|---|---|
|
Modèle 1 |
8 h |
10 h |
14 h |
|
Modèle 2 |
6 h |
6 h |
10h |
|
Modèle 3 |
12 h |
10 h |
18 h |
Le tableau 2 indique le coût horaire par poste de travail :
|
Tableau 2 |
Coût horaire |
|---|---|
|
Poste 1 |
25 €/heure |
|
Poste 2 |
20 €/heure |
|
Poste 3 |
15 €/heure |
-
On considère les matrices suivantes : $H=\begin{pmatrix} 8&10&14\\6&6&10\\12&10&18 \end{pmatrix}$ et $C=\begin{pmatrix} 25\\20\\15 \end{pmatrix}$.
-
Calculer à la main le produit $P=H\times C$.
-
Que représentent les coefficients de la matrice $P$ ?
-
-
Après une étude de marché, le fabricant souhaite que les prix de revient par modèle soient les suivants :
Modèle 1 : 584€ ; Modèle 2 : 402€ ; Modèle 3 : 736€.
Il cherche à déterminer les nouveaux coûts horaires par poste permettant d’obtenir ces prix de revient.
Déterminer pour lui les nouveaux coûts horaires.
Une firme nationale fabrique des commutateurs perfectionnés dans trois usines : l’usine 1, l’usine 2 et l’usine 3.
Les trois usines fabriquent trois modèles différents de commutateurs : A, B et C.
Le nombre de motos produites par heure de travail dans les trois usines est donné dans le tableau suivant :
|
Usine 1 |
Usine 2 |
Usine 3 |
|
|---|---|---|---|
|
A |
1 |
2 |
3 |
|
B |
8 |
5 |
5 |
|
C |
5 |
3 |
3 |
On note $x$, $y$ et $z$ le nombre d’heures de travail respectivement dans l’usine 1, dans l’usine 2 et dans l’usine 3.
On note $a$, $b$ et $c$ le nombre total de commutateurs fabriqués respectivement de modèles A, B et C.
Dans la suite de l’énoncé, on admet que cette situation peut se traduire matriciellement par l'égalité $Y=M\times X$.
-
Déterminer les matrices $M$, $X$ et $Y$.
-
-
Durant une période donnée, 50 h de travail ont été effectuées dans l’usine 1, 30 h dans l’usine 2 et 26 h dans l’usine 3. Donner la matrice $X$ correspondante.
-
Quel est le nombre de commutateurs de modèle A fabriqués pendant cette période ? De modèle B ? De modèle C ?
-
-
Au cours de l’année 2024, ont été fabriquées : 21450 commutateurs de modèle A ; 62350 commutateurs de modèle B ; 38050 commutateurs de modèle C.
Déterminer le nombre d’heures qui ont été nécessaires dans chaque usine pour réaliser cette production. Justifier.
Phénomènes stochastiques
Lorsque l'on effectue une recherche sur Internet avec un moteur de recherche, celui-ci affiche les pages Web du
résultat de la recherche par ordre croissant de pertinence.
La qualité du moteur de recherche est basée sur la notion de pertinence d'une page. Comment définir cette pertinence ?
Comme les pages Web sont reliées les unes aux autres par des liens hypertexte, l'idée consiste à dire qu'une page
Web est d'autant plus pertinente qu'elle est pointée par de nombreuses pages Web, elles aussi pertinentes.
L'algorithme PageRank®, développé par Larry Page, cofondateur avec Sergey Brin de Google, et breveté en 1998,
attribue à chaque page Web une valeur, appelée indice de pertinence, proportionnelle à la probabilité qu'un surfeur,
parcourant le Web en cliquant aléatoirement sur l'un des liens apparaissant sur chaque page, passe par cette page,
au bout d'un très grand nombre de clics.
Une première approche : étude asymptotique du surf sans saut :
Pour simplifier énormément, réduisons le web à trois pages Web, numérotées 1, 2 et 3, reliées entre elles par des liens
hypertexte de la façon schématisée ci-contre : 
-
Le site 1 référence les sites 2 et 3 : on peut donc accéder à ces sites directement depuis le site 1.
-
Le site 2 référence les sites 1 et 3.
-
Le site 3 ne référence que le site 1.
Initialement, un surfeur choisit au hasard l'une des trois pages.
Ensuite, à chaque étape de son surf, il choisit au hasard, donc de manière équiprobable, une page parmi celles
référencées par la page, c'est-à-dire une parmi celles vers lesquelles pointe la page où il se trouve sur le schéma.
Ainsi, le schéma précédent est augmenté des probabilités de suivre un chemin donné.
Ainsi, lorsque le surfeur est sur la page 1, la probabilité qu'il se dirige vers la page 2 est de $\dfrac{1}{2}$ par contre
de la page 3, il est certain d'aller sur la page 1, donc la probabilité est de 1.
D'où le schéma suivant modélisant le Web simplifié :

On s'intéresse désormais à la probabilité de présence du surfeur sur une page donnée au bout de $n$ étapes de surf.
Pour cela, on définit mathématiquement la variable aléatoire $X_n$ qui donne le numéro de la page où se trouve le surfeur
au bout de $n$ clics. Il y a trois valeurs possibles pour $X_n$ : 1, 2 et 3. (les 3 pages du Web simplifié).
Une note $U_n$ la matrice colonne donnant les probabilités d'être à une page donnée au bout de $n$ étapes.
On a donc $U_n=\begin{pmatrix}P(X_n=1)\\P(X_n=2)\\P(X_n=3)\end{pmatrix}$. C'est cette matrice qui donnera,
à un coefficient de proportionnalité près l'indice de pertinence au bout d'un très grand nombre de clics,
c'est-à-dire pour $n$ assez grand.
-
Justifier que si le surfeur débute depuis une page au hasard, alors $U_0=\begin{pmatrix}\frac{1}{3}\\\frac{1}{3}\\\frac{1}{3}\end{pmatrix}$.
-
Déterminer la matrice $A$ telle que pour tout entier $n$, on a : $U_{n+1}=A\times U_n$.
-
Montrer que $U_1=\begin{pmatrix}\frac{1}{2}\\\frac{1}{6}\\\frac{1}{3}\end{pmatrix}$ et que $U_2=\begin{pmatrix}\frac{5}{12}\\\frac{1}{4}\\\frac{1}{3}\end{pmatrix}$.
-
-
Utiliser Xcas pour calculer $U_{10}$ puis $U_{100}$ et enfin $U_{1000}$.
-
Que peut-on conjecturer sur le comportement de la suite $(U_n)$ lorsque le nombre $n$ d'étapes du surf sur ces pages devient grand ?
-
Classer, à partir des résultats affichés par Xcas, les trois pages de la plus pertinentes à la moins pertinente.
-
Les clients d’un restaurant sont des habitués qui y déjeunent tous les jours.
En septembre 2024, le restaurateur propose
trois nouveaux plats : plat A, plat B et plat C. D’un jour à l’autre, il constate que :
-
Parmi les clients ayant choisi le plat A : 30 % reprennent le plat A le lendemain, 50 % prennent le plat B le lendemain.
-
Parmi les clients ayant choisi le plat B : 30 % reprennent le plat B le lendemain, 60 % prennent le plat A le lendemain.
-
Parmi les clients ayant choisi le plat C : 35 % prennent le plat A le lendemain, 45 % prennent le plat B le lendemain.
On note pour tout entier $n$ non nul :
-
$a_n$ la proportion de clients ayant choisi le plat A le $n$-ième jour.
-
$b_n$ la proportion de clients ayant choisi le plat B le $n$-ième jour.
-
$c_n$ la proportion de clients ayant choisi le plat C le $n$-ième jour.
Pour tout entier $n\ge 1$, on note $P_n=\begin{pmatrix} a_n\\b_n\\c_n\end{pmatrix}$ l’état probabiliste le $n$-ième jour.
-
Représenter cette situation en reproduisant et en complétant le graphe probabiliste suivant :

-
Donner la matrice de transition $M$ de ce graphe, en respectant l’ordre alphabétique des sommets, c'est-à-dire la matrice $M$ telle que pour tout entier naturel non nul $n$ : $P_{n+1}=M\times P_n$.
-
Le restaurateur a noté que, le premier jour, 35,5 % des clients ont pris le plat A, 40,5 % ont pris le plat B et 24 % ont pris le plat C.
Donner la matrice $P_1$. -
Calculer $P_2$.
-
Le restaurateur affirme que le douzième jour, la proportion de clients qui choisiront le plat C sera à peu près la même que le treizième jour, soit environ 15,9 %. A t il raison ? Justifier.
-
Déterminer la proportion de clients pour chacun des plats à très long terme.
On considère un réseau de commutation de paquets constitués de 6 routeurs A, B, C, D, E et F.
Chaque paquet reçu par l’un des routeurs doit être acheminé vers un autre routeur, jusqu’à
atteindre sa destination finale.
On a résumé les règles de routage d’un routeur à un autre routeur par le graphe orienté $G$ constitué
des sommets A, B, C, D, E et F. Les sommets représentent les routeurs.
Si un sommet X peut transmettre un paquet vers un sommet Y alors on a l’arc : X → Y.
Voici ce graphe $G$ :
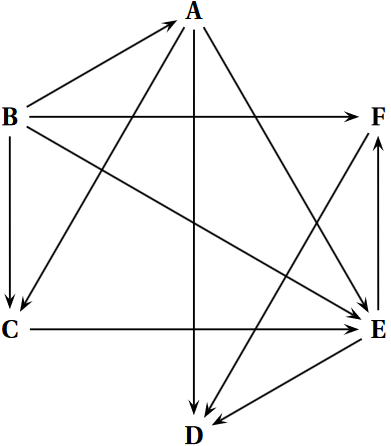
-
Compléter le tableau suivant donnant les prédécesseurs et les successeurs de chaque sommet du graphe $G$ :
Sommets Prédécesseurs Successeurs A B C D E F -
La matrice d'adjacence $M$ du graphe $G$ est la matrice dont le terme général $m_{ij}$ vaut :
-
1 s'il existe un arc reliant le sommet de la ligne $i$ au sommet de la colonne $j$ dans le graphe $G$.
-
0 s'il n'existe pas un tel arc dans le graphe $G$.
Compléter la matrice $M$ : $\begin{pmatrix}...&0&1&...&...&...\\ ...&...&...&...&...&... \\ ...&...&...&...&...&... \\ ...&...&...&...&...&...\\ ...&...&...&...&...&... \\ ...&...&...&...&...&...\end{pmatrix}$.
Le terme $m_{12}$ valant 0 dans la matrice ci-dessus signifie qu'il n'existe pas d'arc reliant le sommet A au sommet B.
Le terme $m_{13}$ valant 3 dans la matrice ci-dessus signifie qu'il existe un arc reliant le sommet A au sommet C. -
-
Pour tout entier $n$ non nul, on considère la matrice puissance $M^n$.
On admet que le coefficient de la ligne $i$ et de la colonne $j$ de cette matrice puissance donne le nombre de chemins allant du sommet de la ligne $i$ au sommet de la colonne $j$ de longueur $n$, c'est-à-dire le nombre de possibilités pour passer du sommet $i$ à celui $j$ en passant par exactement $n$ arcs se succédant sans saut.
Calculer $M^4$.
En déduire le nombre de chemins de longueur 4 allant du sommet B au sommet D. -
La matrice de fermeture transitive $T$ de ce graphe $G$ est une matrice carrée d’ordre 6 formée de 0 et de 1 telle que :
-
On met un 1 à l’intersection de la ligne correspondant au sommet X et de la colonne correspondant au sommet Y s’il existe au moins un chemin allant du sommet X au sommet Y.
-
On met un 0 si un tel chemin n'existe pas.
On admet que pour trouver cette matrice de fermeture transitive $T$, il suffit de calculer la matrice somme $M+M^2+M^3+M^4+M^5+M^6$ puis de remplacer dans cette matrice somme obtenue chaque nombre non nul par le nombre 1.
Déterminer la matrice de fermeture transitive $T$ associée au graphe $G$.
-
Demander le programme !
-
La notion de matrice.
-
Le vocabulaire sur les matrices.
-
La notion de matrice unité.
-
La notion de matrice inversible.
-
Savoir additionner ou soustraire deux matrices à la main.
-
Savoir à la main multiplier une matrice par un réel.
-
Savoir à la main multiplier deux matrices.
-
Savoir saisir une matrice sur Xcas.
-
Savoir utiliser Xcas pour effectuer du calcul matriciel.
-
Savoir déterminer sur Xcas la matrice inverse d'une matrice inversible.
-
Savoir modéliser un problème concret sous forme d'un système.
-
Savoir réécrire un système en tant que produit matriciel.
-
Savoir modéliser des phénomènes stochastiques à l'aide de matrices.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International