Asymptote verticale
Asymptote verticale
On dit que $f$ admet une asymptote verticale en $a$ si $\lim\limits_{x\to a} f(x)=+\infty$ ou/et si $\lim\limits_{x\to a} f(x)=-\infty$
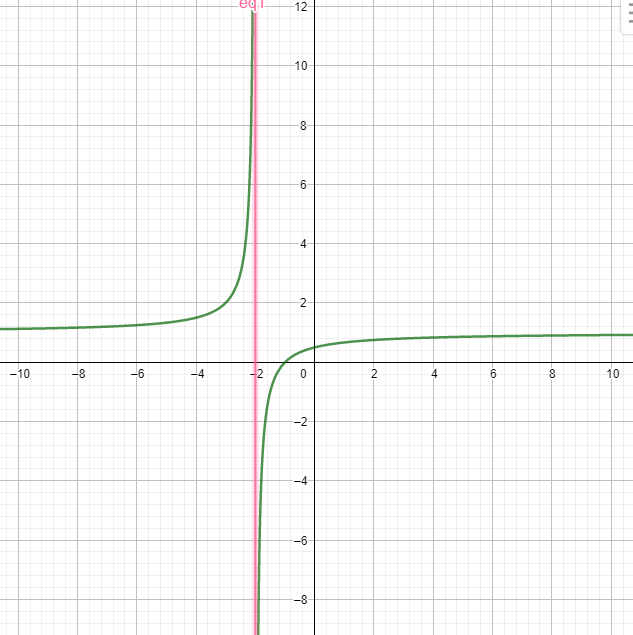
Observez que sur cet exemple que $\lim\limits_{x\to -2^{+}} f(x)=-\infty$ et $\lim\limits_{x\to -2^{-}} f(x)=+\infty$.
On dit que $f$ admet en -2 une asymptote verticale.
Asymptote horizontale
Asymptote horizontale
On dit que $f$ admet une asymptote horizontale en $+\infty$ si $\lim\limits_{x\to +\infty} f(x)=a$ avec $a$ réel.
De la même manière, On dit que $f$ admet une asymptote horizontale en $-\infty$ si $\lim\limits_{x\to -\infty} f(x)=a$ avec $a$ réel.

Observez que sur cet exemple que $\lim\limits_{x\to +\infty} f(x)=1$.
On dit que $f$ admet en $+\infty$ une asymptote horizontale.
De la même manière, $\lim\limits_{x\to -\infty} f(x)=1$. $f$ admet en $-\infty$ une asymptote horizontale.
Représentez (dans geogebra) les fonctions définies ci dessous et indiquez les éventuelles asymptotes :
- $f(x)=exp(-x)$
- $f(x)=x*exp(-x)$
- $f(x)=ln(x)$
- $f(x)=\frac{x}{2x+1}$
- $f(x)=\frac{1}{x²+1}$
Etude n°1
Soit le fonction $f$ définie sur $]0;+\infty[$ par $f(x)=2x+1+\frac{1}{x^2}$.
On note $\mathcal{C}$ sa représentation graphique.
-
- Déterminer les limites de $f$ aux bornes de son ensemble de définition.(Xcas)
- En déduire que la courbe admet une asymptote dont on précisera une équation.
-
- Déterminer la fonction dérivée de $f$.(Xcas)
- Résoudre $f'(x)<0$.
- Établir le tableau de variation.
- Vérifier les variations à l'aide de Géogebra.
- Sur le même graphique représenter la droite D d'équation $y=2x+1$. Que dire?
- Déterminer la limite en $+\infty$ de $f(x)-(2x+1)$.
Asymptote oblique.
On dit que la droite d'équation $y=ax+b$ est asymptote oblique de la courbe représentative de $f$ si $\lim\limits_{x\to +\infty} f(x)-(ax+b)=0$ ou/et si $\lim\limits_{x\to -\infty} f(x)-(ax+b)=0$
Montrer que $y=x$ est asymptote oblique à $f:x\longmapsto \frac{x^2+6x+4}{x+6}$.