TP2: Les fonctions.
Dans ce tp , nous allons apprendre à manipuler les fonctions avec les outils numérique à notre disposition : xcas et geogebra
Calculer une image , antécédent...
Déterminer pour chacune des fonctions suivantes l'image de 0; -1; 2; 4 et 5 :
- $f(x)=x^2-3x+2$
- $g(x)=\frac{2x+1}{x-5}$
- $h(x)=\frac{x+1}{(x-1)(5-x)}$
En xcas pour manipuler une fonction , il faut l'implementer
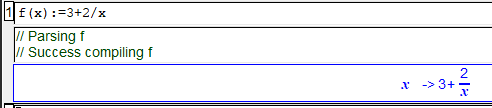
On procedera ainsi pour chaque exercice qui utilisera des fonctions.
Pour calculer une impage par exemple 1 ; on procédera ainsi :

Détermination d'antécédents
Rappelez vous que chercher l'antécédent d'un nombre $a$ par $f$ c'est déterminer toutes les solutions de $f(x)=a$.
Déterminer les antécédents de 0;-1;2 par les fonctions suivantes s'ils existent.
- $f(x)=x^2-3x+2$
- $g(x)=\frac{2x+1}{x-5}$
- $h(x)=\frac{x+1}{(x-1)(5-x)}$
Déterminer le signe d'une fonction
Déterminer le signe d'une fonction c'est réaliser le tableau de signe d'une fonction.
par exemple le signe de $f:\longmapsto \frac{x-1}{x+2}$ est donné par le tableau :
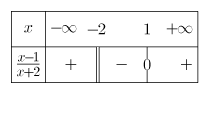
Le "$-$" de la dernière ligne signifie que $f(x)\leq0$ pour $x\in]-2;1]$
Les "$+$" de la dernière ligne signifie qur $f(x)\geq0$ pour $x\in]-\infty;-2[\cup[1;+\infty[$
Déterminer le signe des fonctions suivantes
- $f(x)=x^2-3x+2$
- $g(x)=\frac{2x+1}{x-5}$
- $h(x)=\frac{x+1}{(x-1)(5-x)}$
En xcas la détermination du signe ce fait avec une résolution d'inéquation et ne nous posera pas de problème.
En attendant que je trouve une solution pour faire un taleau de signe, procédez comme dans l'exemple là
C'est pour réaliser des tableaux en word qu'il y aura un peu plus de travail :
Commencer par télécharger ce fichier
Décompresser ce fichier dans un répertoire "sineq" dans votre répertoire documents ( ou sur votre clé usb)
Le logiciel sine qua non est un logiciel libre sans installation dans cette version.