Algorithmique et langage python.
Voici une liste d'algorithmes pour vous permettre de vous initier à la trace d'exécution d'algorithmes ainsi qu'au langage de programmation python.
1. x ← 0 2. y ← -1 3. Si x < y alors 4. x ← x+y 5. sinon 6. y ← x-y
- Faire la trace d'exécution de cet algorithme.
- Recommencez avec x=-2 et y=-1
Voici l'algorithme en langage python :
Utiliser cet espace pour faire la question 2
Voici un algorithme :
a ← 24 b ← 12 c ← -4 d ← a+b+c Afficher(d)
Quelle est la valeur de d ? Transformer cet algorithme en langage python. Faire des essais en changeant les valeurs des variables.
Si vous voulez entrer une valeur au clavier, vous pouvez taper :
a=float(input("entrer la valeur de a"))On considère l'algorithme suivant :
1. saisir(a) 2. saisir(b) 3. si a < b alors 4. c ← b+2a 5. sinon 6. c ← a-2b 7. afficher(c)
- Faire la trace d'exécution de cet algorithme avec a=1 et b=-2. Refaire avec a=-3 et b=4.
- Programmer en langage python cet algorithme
Pour aller plus loin
En Python, # permet d'écrire un commentaire.
Pour compiler et exécuter un programme, il faut utiliser la touche  .
.
Aspect général d'Edupython
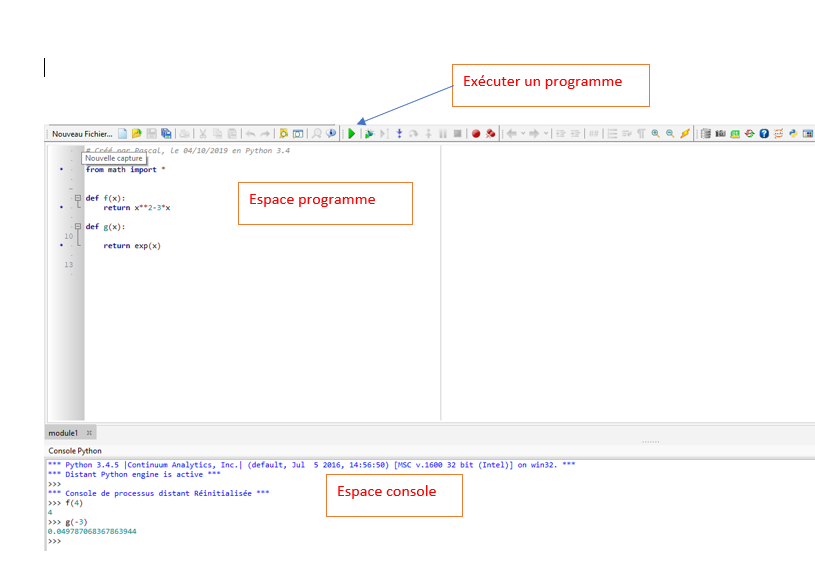
Les fonctions.
Un exemple de définition de fonctions avec Python
from math import * # Importation d'une bibliothèque pour faire de maths.
def f(x):
return x**2+3*x+1
print(f(10)) # Une seule valeur.
# Plusieurs valeurs
for x in range(100): # range(100) génère une liste d'entiers de 0 à 99.
print(f(x))
Définir des fonctions en lien avec le cours actuel pour conjecturer des limites.
valeurs_x=[x for x in range(30)] # permet de créer une liste de 30 valeurs.
valeurs_f=[f(x) for x in range(30)] # permet de créer un tableau de valeurs.
# valeurs_f=[f(x) for x in valeurs_x] donne le même tableau de valeurs, à tester.
Donner la tableau de valeurs de la fonction définie par $f(x)=x²+3x-1$ pour les valeurs de $x$ comprise entre 0 et 50 (avec un pas de 1)
from math import *
import numpy as np
lx=np.linspace(-10,10,100)
Dans la console, éditer les valeurs de lx. Que représente cette liste de valeurs ?
Compléter votre programme pour afficher la table des valeurs pour les valeurs de $x$ contenues dans lx
Tester le code suivant :
a=-30
b=50
n=1000
lx=np.linspace(a,b,n)
# Penser à afficher lx dans la console
Ecrire une fonction tableau_valeurs(f,a,b,n) qui affiche le tableau des $n$ valeurs comprises entre $a$ et $b$.
def tableau_valeurs(f,a,b,n) :
lx = # A compléter
valeurs_f = # A compléter
return lx,valeurs_f
Affichage des points
On peut facilement tracer les nuages de points correspondants, en utilisant les fonctions du module matplotlib.
On importe le sous-module pyplot de matplotlib qu’on renomme au passage plt
import matplotlib.pyplot as plt
(v_x, v_y) = tableau_valeurs(f ,-10,10,100)
plt.plot(v_x , v_y , ' . ' , color='red')
plt.show()
Faire des tests avec des fonctions utilisées en classe.
Le second degré
Il s'agit d'implémenter le cours sur les formules que vous connaissez sur le second degré. Vous pourrez structurer votre document avec de nombreuses fonctions. Reprenez le cours afin d'avoir toutes vos formules avec vous.
Ecrire une fonction delta avec comme arguments a,b,c et qui retourne le discriminant du pôlynome. Faire des tests avec des exxemples traités en cours.
Ecrire une fonction nombre_racines avec comme arguments a,b,c et qui retourne le nombre de racines du polynôme. Faire des tests avec des exxemples traités en cours.
Ecrire une fonction racines avec comme arguments a,b,c et qui retourne les racines du polynôme. Faire des tests avec des exxemples traités en cours.
Essayer de construire un programme complet qui traite toutes les formules du cours.
Quelques aides :
from math import *
# Calcul de delta
def delta(a,b,c):
return b**2-4*a*c
# calcul des racines
def racines(a,b,c) :
dis=delta(a,b,c)
if dis < 0 : return None
elif dis==0 : return -b/(2*a) # Attention aux parenthèses
else : return ((-b-sqrt(dis))/(2*a),(-b+sqrt(dis))/(2*a)) # Attention aux parenthèses
Faire des tests avec votre programme.
print(racines(1,1,1))
print(racines(1,-2,1)
print(racines(1-3,-4)
Compléter votre code avec une fonction nombre_racines(a,b,c) qui retourne le nombre de racines du polynôme
Ecrire une fonction utilsateur() qui demande en lecture les valeurs de a,b,c et qui affiche les racines du polynôme si elles existent.
Par exemple :
# Une idée de représentation d'un polynôme.
def eval_p(p,x):
return p[0]*x**2+p[1]*x+P[2]
# p[0] correspond à a, p[1] correspond à b, p[2] correspond à c.
p=(2,3,1) # p(x)=2x²+3x+1, p est codé par ses coefficients
# Pour calculer p(4)
eval_p(p,4)
Quelques vidéos.
Il s'agit d'implémenter le cours sur les formules que vous connaissez sur le second degré. Vous pourrez structurer votre document avec de nombreuses fonctions. Reprenez le cours afin d'avoir toutes vos formules avec vous.
Ecrire une fonction delta avec comme arguments a,b,c et qui retourne le discriminant du pôlynome. Faire des tests avec des exxemples traités en cours.
Ecrire une fonction nombre_racines avec comme arguments a,b,c et qui retourne le nombre de racines du polynôme. Faire des tests avec des exxemples traités en cours.
Ecrire une fonction racines avec comme arguments a,b,c et qui retourne les racines du polynôme. Faire des tests avec des exxemples traités en cours.
Essayer de construire un programme complet qui traite toutes les formules du cours.
Quelques aides :
from math import *
# Calcul de delta
def delta(a,b,c):
return b**2-4*a*c
# calcul des racines
def racines(a,b,c) :
dis=delta(a,b,c)
if dis < 0 : return None
elif dis==0 : return -b/(2*a) # Attention aux parenthèses
else : return ((-b-sqrt(dis))/(2*a),(-b+sqrt(dis))/(2*a)) # Attention aux parenthèses
Faire des tests avec votre programme.
print(racines(1,1,1))
print(racines(1,-2,1)
print(racines(1-3,-4)
Compléter votre code avec une fonction nombre_racines(a,b,c) qui retourne le nombre de racines du polynôme
Ecrire une fonction utilsateur() qui demande en lecture les valeurs de a,b,c et qui affiche les racines du polynôme si elles existent.
Par exemple :
# Une idée de représentation d'un polynôme.
def eval_p(p,x):
return p[0]*x**2+p[1]*x+P[2]
# p[0] correspond à a, p[1] correspond à b, p[2] correspond à c.
p=(2,3,1) # p(x)=2x²+3x+1, p est codé par ses coefficients
# Pour calculer p(4)
eval_p(p,4)
Voici quelques vidéos afin de vous familiariser avec le langage PYTHON.
Le mieux est d'ouvrir le logiciel EduPYTHON ou le logiciel JUPYTER et de pratiquer en même temps que la vidéo
Utilisation de la console EDUPYTHON :
Les fonctions (en mode console EDUPYTHON) :
Les boucles
Présentation de JUPYTER :