A5 : Décomposition d'un entier en produit de facteurs premiers.

Infinité des nombres premiers

Tout entier naturel supérieur ou égal à 2 est divisible par un nombre premier.

Démontrer la propriété 1 par récurrence.
On notera $(P_n)$ : "Tout entier naturel compris entre 2 et $n$ admet un diviseur premier."

Il y a une infinité de nombre premier.

Démontrer la propriété 2.

Raisonner par l'absurde qu'il y a un nombre fini de nombres premiers. Notons $n$ l'effectif de ces nombres.

On peut noter alors $p_1$, $p_2$, ..., $p_n$ les nombres premiers.

On considérera le nombre $m=p_1\times p_2\times...\times p_n+1$

Décomposition en produit de facteurs premiers

Théorème fondamental de l'arithmétique

Tout entier $n$ supérieur ou égal à 2 se décompose en produit de facteurs premiers.

Autrement dit :

Pour tout entier naturel $n\geq 2$ , ils existent $k$ nombres premiers : $p_1$, $p_2$, ..., $p_k$ et k entiers naturels :$\alpha_1$, $\alpha_2$, ..., $\alpha_k$ tels que $$n=p_1^{\alpha_1}\times p_2^{\alpha_2}\times ...\times p_k^{\alpha_k}$$

Cette décomposition est unique à l'ordre des facteurs près.

Ce théorème est parfois appelé le théorème fondaental de l'arithmétique.

Ce théorème signifie qu'il y a l'existence d'une telle décomposition puis aussi son unicité.
La démonstration doit donc se faire en deux temps.

Existence :
Démontrer l'existence par récurrence.
On notera $(P_n)$ : "Tout entier naturel compris entre 2 et $n$ se décompose en produit de facteur premier."
Unicité :
Démontrer l'unicité.

On pourra supposer qu'il y a deux décompositions et ordonner les facteurs premiers. Il suffit de comparer les exposants apparaissant dans chaque décomposition.

Pour décomposer un nombre $n$, par exemple 750, en produit de nombres premiers, il suffit :

Méthode 1 :

Effectuer une série de divisions par les plus petits nombres premiers jusqu'à obtenir 1.

D'où la décomposition : $750=2^1\times 3^1\times 5^3$.
Méthode 2 :

On cherche à écrire $n$ comme produit de deux nombres $a$ et $b$ strictement plus petits.
On décompose chaque facteur plus petit jusqu'à obtenir seulement des nombres premiers.

$750=75\times 10=(3\times 25) \times (5\times 2)= (3\times (5\times 5)) \times (5\times 2)=2^1\times 3^1\times 5^3$.

Décomposer en produit de nombres premiers les nombres suivants :
1. 96.
2. 1089.
3. 10920.
En déduire une simplification de la fraction $\dfrac{96}{10920}$.

Utilisation

Soit $n$ un nombre entier naturel supérieur ou égal à 2 dont la décomposition en produit de facteurs premiers est : $n=p_1^{\alpha_1}\times p_2^{\alpha_2}\times ...\times p_k^{\alpha_k}$ (les $p_i$ sont des nombres premiers distincts et les exposants $\alpha_i$ sont des nombres entiers naturels non nuls).

Le nombre de diviseurs de $n$ est égal à $(\alpha_1+1)\times (\alpha_2+1) \times ... \times (\alpha_k+1)$.

Démontrer cette propriété.

Pour déterminer la liste des diviseurs d'un nombre, il suffit de :

décomposer ce nombre en facteur de nombres premiers,
Énumérer tous les diviseurs possibles en listant tous les combinaisons de puissances possibles, éventuellement avec un arbre.

Exemple : obtenir l'ensemble des diviseurs de $18$ :

$18=2\times 3= 2^1\times 3^2$.

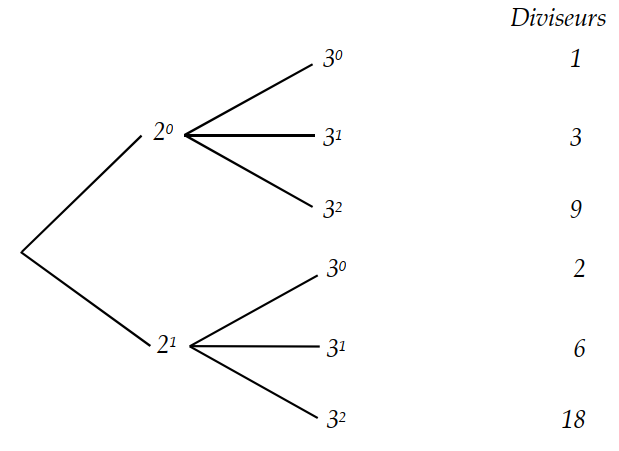
Ainsi, $18$ possèdent $6$ diviseurs : 1, 2, 3, 6, 9 et 18.

Déterminer le nombre de diviseurs de 1400.
Déterminer l'ensemble des nombres divisant 1400.

Soient $a$ et $b$ deux entiers non nuls.

On appelle Plus Petit Commun Multiple de $a$ et de $b$ le plus petit des multiples communs positifs de $a$ et de $b$.
On le note PPCM(a;b).

Un tel nombre existe car l'ensemble des nombres entiers positifs muliples de $a$ et de $b$ est une partie non vide de $\mathb{N}$ (car contenant le nombre $ab$) : cet ensemble admet donc un minimum.

Soient $a$ et $b$ deux nombres entiers naturels supérieurs ou égaux à $2$.
Quitte à considérer des exposants nuls, on peut supposer que $a$ et $b$ peut être décomposer sous forme de produit de facteurs premiers comme suivant :
$a=p_1^{\alpha_1}\times p_2^{\alpha_2}\times ...\times p_k^{\alpha_k}$
$b=p_1^{\beta_1}\times p_2^{\beta_2}\times ...\times p_k^{\beta_k}$
(les $p_i$ sont des nombres premiers distincts et les exposants $\alpha_i$ et $\beta_i$ sont des nombres entiers naturels éventuellement nuls).

On a alors :

$PGCD(a;b)=p_1^{min(\alpha_1;\beta_1)}\times p_2^{min(\alpha_2;\beta_2)}\times ...\times p_k^{min(\alpha_k;\beta_k)}$
$PPCM(a;b)=p_1^{max(\alpha_1;\beta_1)}\times p_2^{max(\alpha_2;\beta_2)}\times ...\times p_k^{max(\alpha_k;\beta_k)}$

Déterminer le PGCD et le PPCM des entiers 3757 et 2873.

Démontrer que pour tout entier naturel non nul $a$ et $b$ : $PGCD(a;b)\times PPCM(a;b)=a\times b$.

Exercices

Donner la décomposition en facteus premiers des nombres 1960 et 1120.
En déduire le forme irréductible de la fraction $\dfrac{1120}{1960}$.

Décomposer $900^{900}$ est produit de nombres premiers.
En déduire le nombre de diviseurs de $900^{900}$.
Démontrer qu'il existe un nombre entier admettant au moins mille milliards de diviseurs.
Soit $n$ un entier strictement positif.
On note $d$ le nombre de diviseurs premiers de $n$.
Démontrer que $\ln(n)\ge d \times \ln(2)$.

Décomposer 255 en produit de nombres premiers.
Déterminer les solutions entières naturels de l'équation $(n-1)(n+2)=255$.
Déterminer les solutions entières naturels de l'équation $3n^2+6n-105=255$.

Compléter la fonction diviseurs suivante de sorte qu'elle renvoie la liste des diviseurs du nombre n saisi comme argument de la fonction.
```
def diviseurs(n):
    lst = ... 
    for i in range(...):
        if n%i == 0:
            lst.append(...)
    return lst
```
Compléter la fonction est_premier suivante de sorte qu'elle renvoie True dans le cas où le nombre n saisi comme argument de la fonction est un nombre premier et False dans les autres cas.
Cette fonction utilise la fonction diviseurs précédente.
```
def est_premier(n):
    boole = ... 
    if len(diviseurs(n)) ...:
        if n%i == 0:
            boole = ...
    return boole
```
Compléter la fonction liste_facteurs_premiers suivante de sorte qu'elle renvoie la liste des facteurs premiers du nombre n saisi comme argument de la fonction.
Cette fonction utilise la fonction est_premier précédente.
```
def liste_facteurs_premiers(n):
    lst = ... 
    for i in range(...):
        if est_premier(...):
            if n%i ... 0:
                ...
    return lst
```
Utiliser les fonctions précédentes pour décomposer le nombre $n=184796292581038600$ en produit de nombres premiers.

Déterminer l'ensemble des entiers naturels non nuls $n$ et $m$ tels que $PGCD(m;n)=12$ et $PPCM(m;n)=60$.

On désigne par $d(n)$ le nombre de diviseurs strictement positifs de l’entier $n$.
Montrer que $d(n)$ est impair si, et seulement si, $n$ est un carré.

Combien de zéors faut-il écrire de sorte que le nombre $n=900...0$ admette exactement 108 diviseurs ?

Savoirs et savoir-faire

Savoir qu'il existe une infinité de nombres premiers.
Savoir que tout nombre entier naturel supérieur ou égal à 2 se décompose (de manière unique à l'ordre près des facteurs) produit de nombres premiers.
Savoir la définition du PPCM de deux nombres entiers non nuls.

Savoir décomposer un nombre entier en produit de nombres entiers.
Savoir déterminer l'ensemble des diviseurs d'un nombre entier.
Savoir déterminer le nombre de diviseurs d'un nombre entier.
Savoir déterminer le PGCD (et le PPCM) de deux entiers $a$ et $b$ à l'aide de leur décomposition sous forme de produit de nombres premiers.

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲