Le cours complet avec les exercices du chapitre est disponible en version imprimable en cliquant ici.
Demander le programme !

Forme algébrique d'un nombre complexe.
Définitions générales.
Si vous voulez découvrir une brève histoire des nombres en mathématiques avec un survol de l'apparition des nombres complexes, vous pouvez visionner en cliquant directement sur ce lien ou directement ci-dessous :
-
Un nombre complexe est un élément de la forme $x+iy$ , où $x$ et $y$ sont des réels et $i$ un nombre imaginaire vérifiant $i^2=-1$.
-
L'ensemble des nombres complexes est noté $\mathbb{C}$.
$2+3i~;~i+1,5~;~2;~-4i~;~\pi+\sqrt2i$ sont des nombres complexes.
L'écriture $x+iy$, où $x\in\mathbb{R} \textrm{ et } y\in\mathbb{R}$, d'un nombre complexe $z$ est appelée la forme algébrique du nombre complexe $z$.
Partie imaginaire et partie réelle d'un nombre complexe
Soit $z$ un complexe de forme algébrique $x+iy$.
-
Le nombre réel $x$ est appelé la partie réelle de $z$ notée $Re(z)$.
-
Le nombre réel $y$ est appelé la partie imaginaire de $z$ notée $Im(z)$.
Déterminer les partie réelle et imaginaire des complexes suivants :
- $z_1=5+2i$
- $z_2=2-8i$
- $z_3=3$
- $z_4=-2i$
- $z_5=2i+1$
-
L'ensemble des nombres réels est inclus dans l'ensemble des nombres complexes : $\mathbb{R}\subset\mathbb{C}$
-
$Re(z)$ et $Im(z)$ sont des nombres réels.
Un nombre complexe de forme algébrique $iy$ avec $y\in\mathbb{R}$ est appelé imaginaire pur.
L'ensemble des nombres complexes imaginaires purs peut être noté $i\mathbb{R}$.
Soient $z$ et $z'$ deux nombres complexes.
Deux complexes sont égaux si et seulement si leurs parties réelles et imaginaires sont égales.
$z=z'$ si et seulement si $Re(z)=Re(z')$ et $Im(z)=Im(z')$.
Idées de la démonstration : travailler par double implication et utiliser un raisonnement par l'absurde pour le sens réciproque
On note $x+iy$ et $x'+iy'$ les formes algébriques des nombres complexes $z$ et $z'$ respectivement.
$\Leftarrow$ : Si $Re(z)=Re(z')$ et $Im(z)=Im(z')$ alors $x=x'$ et $y=y'$ ainsi $z=x+iy=x'+iy'=z'$.
$\Rightarrow$ : à vous de jouer
Le but de cet exercice est de montrer le sens réciproque du théorème précédent : si $z=z'$ alors $Re(z)=Re(z')$ et $Im(z)=Im(z')$.
On note $x+iy$ et $x'+iy'$ les formes algébriques des nombres complexes $z$ et $z'$ respectivement.
On suppose que $x+iy=x'+iy'$.
-
Démontrer grâce à un raisonnement par l'absurde que $y=y'$.( on cherchera à exprimer $i$ en fonction de $x$, $x'$, $y$ et $y'$.)
-
En déduire que l'on a aussi $x=x'$.
Ce théorème implique que la forme algébrique d'un nombre complexe est unique.
-
$z$ est un réel si et seulement si $Im(z)=0$.
-
$z$ est un imaginaire pur si et seulement si $Re(z)=0$.
-
$z=0$ si et seulement si $Re(z)=0$ et $Im(z)=0$.
Ces 3 propriétés découlent directement du théorème précédent garantissant l'unicité de la forme algébrique
Prenons par exemple la 2. :
Idées de la démonstration : travailler par double implication
On note $x+iy$ la forme algébrique du nombre complexe $z$.
$\Leftarrow$ : Si $Re(z)=0$ alors $z=iy$ : par définition, $z$ est un imaginaire pur.
$\Rightarrow$ : Si $z$ est nombre imaginaire pur alors il peut s'écrire sous la forme $z=iy'$
D'après l'unicité de la forme algébrique d'un nombre complexe, on a : $x=0$ et $y=y'$ donc $Re(z)=0$.
Dans chacun des cas suivants, déterminer les réels $x$ et $y$ vérifiant l'égalité :
- $(2-x)+i(2y-3)=4+6i$.
- $(x+y)+i(2x-y-4)=0$.
Opérations sur les nombres complexes
Addition et multiplication sur les nombres complexes
$\mathbb{C}$ peut être muni ainsi d'une addition et d'une multiplication qui prolongent celles de $\mathbb{R}$ et pour lesquelles les règles de calcul restent les mêmes.
Soient deux nombres complexes $z$ et $z'$ de formes algébriques $x+iy$ et $x'+iy'$.
-
Somme : $z+z'=(x+x')+i(y+y')$
-
Produit : $zz'=(xx'-yy')+i(xy'+x'y)$
Comme la multiplication suit les mêmes règles que celles dans $\mathbb{R}$, développer l'expression suivante : $(x+iy) \times (x'+iy')$.
Effectuer les calculs suivants :
-
$2+3i-(3-5i)$
-
$(1+i)\left(2-\dfrac{1}{2}i\right)$
Conjugaison
Nombre conjugué
On appelle nombre conjugué du nombre complexe $z=x+iy$ le nombre complexe noté $\overline{z}$ de forme algébrique $x-iy$.
Donnez les conjugués des complexes suivants :
- $z_1=-5-i$
- $z_2=2-3i$
- $z_3=4i-3$
$z+\overline{z}=2Re(z)$ et $z-\overline{z}=2iIm(z)$.
Soit $z$ un nombre complexe.
$z+\overline{z}=Re(z)+iIm(z)+Re(z)-iIm(z)=2Re(z)$
$z-\overline{z}=Re(z)+iIm(z)-Re(z)+iIm(z)=2iIm(z)$
Pour tous nombres complexes $z$ et $z'$ et pour tout entier naturel $n$.
-
$z$ est réel si et seulement si $\overline{z}=z$.
-
$z$ est imaginaire pur si et seulement si $\overline{z}=-z$.
-
$\overline{\overline{z}}=z$
-
$\overline{z+z'}=\overline{z}+\overline{z'}$.
-
$\overline{z \times z'}=\overline{z} \times \overline{z'}$.
-
$\overline{z^n}=\overline{z}^n$.
Toutes ces propriétés se démontrent à l'aide de la forme algébrique.
-
Idée de la démonstration pour ce point : par double implication.
(sens direct) On suppose que $z$ est un réel : $z=Re(z)$. Alors $Im(z)=0$ et donc $\overline{z}=Re(z)+i\times 0=Re(z)=z$.
(sens réciproque) On suppose que $z=\overline{z}$ donc $Re(z)+iIm(z)=Re(z)-iIm(z)$ et par unicité de la forme algébrique d'un complexe, on en déduit donc $Re(z)=Re(z)$ et $Im(z)=-Im(z)$. D'où $Im(z)=0$ : $z$ est un réel.
-
De la même manière que ci-dessus.
-
De la même manière que ci-dessus.
-
$\overline{z+z'}=Re(z+z')-iIm(z+z')$ $=Re(z)+Re(z')-iIm(z)-iIm(z')$ $=(Re(z)-iIm(z))+(Re(z')-iIm(z'))$ $=\overline{z}+\overline{z'}$
-
démonstration à savoir faire ! cf. exercice ci-dessous.
-
démonstration à savoir faire ! cf. exercice ci-dessous.
Soient $z$ et $z'$ deux nombres complexes de forme algébrique respective $x+iy$ et $x'+iy'$.
Montrer que $\overline{z \times z'}=\overline{z}\overline{z'}$.
Soient $z$ un nombre complexe de forme algébrique $x+iy$.
Montrer que pour tout entier naturel $n$, on a : $\overline{z^n}=\overline{z}^n$.
Résoudre dans $\mathbb{C}$ les équations suivantes :
-
$\overline{2z+5+2i}=\overline{3 \times (z+1)}+1+i$
-
$2z+i\overline{z}=5-2i$
Voici la propriété essentielle sur le conjugué :
Soit $z$ un nombre complexe dont la forme algébrique est $x+iy$.
$z \times \overline{z}= x^2+y^2$.
Développer $(x+iy) \times \overline{x+iy}$ pour le prouver.
Inverse et division sur les nombres complexes
Soit $z$ un nombre complexe de forme algébrique $x+iy$.
Si $z\neq 0$ alors : $\dfrac{1}{z}=\dfrac{\overline{z}}{z \overline{z}}$, c'est-à-dire :
Si $z\neq 0$ alors : $\dfrac{1}{z}=\dfrac{1}{x+iy}=\dfrac{x-iy}{(x+iy)\times(x-iy)}=\dfrac{x}{x^2+y^2}+i\dfrac{-y}{x^2+y^2}$.
Effectuer le calcul suivant :
$\dfrac{1}{-1+3i}$
Voici une vidéo qui reprend la méthode de l'inverse de deux nombres complexes, méthode illustrée par la résolution de l'exercice précédent.
Quotient
Soit $z$ et $z'$ deux complexes de forme algébrique $x+iy$ et $x'+iy'$.
Si $z'\neq 0$ alors : $\dfrac{z}{z'}=z\times\dfrac{1}{z'}$.
Soit $z$ et $z'$ deux complexes de forme algébrique $x+iy$ et $x'+iy'$.
Pour calculer une division $\dfrac{z}{z'}$, on multiplie le numérateur et le dénominateur par $\overline{z'}$ le conjugué de $z'$.
Ainsi, $\displaystyle{\dfrac{z}{z'}=\dfrac{x+iy}{x'+iy'}=\dfrac{(x+iy)\times(x'-iy')}{(x'+iy')\times(x'-iy')}=\dfrac{xx'+yy'}{x'^2+y'^2}+i \times\dfrac{x'y-xy'}{x'^2+y'^2}}$
Effectuer le calcul suivant :
$\dfrac{3+2i}{1-i}$
Voici une vidéo qui reprend la méthode de la division de deux nombres complexes, méthode illustrée par la résolution de l'exercice précédent.
$zz'=0$ si et seulement si $z=0$ ou $z'=0$.
Résoudre l'équation suivante :
$(z-2)(2z-1+i)=0$
Résoudre l'équation $2z-3i=(z-5)(1+i)$.
Pour tous nombres complexes $z$ et $z'$ et pour tout entier naturel $n$.
Si $z'\ne 0$ alors $\overline{\dfrac{1}{z'}}=\dfrac{1}{\overline{z'}}$ et $\overline{(\dfrac{z}{z'})}=\dfrac{\overline{z}}{\overline{z'}}$.
Soit $z$ un complexe non nul.
$\overline{(\dfrac{1}{z})}\times \overline{z}=_{(4)} \overline{\dfrac{1}{z}\times z}=\overline{1}=1$.
Ainsi $\overline{(\dfrac{1}{z})}\times \overline{z}=1$ et $\overline{(\dfrac{1}{z})}=\dfrac{1}{\overline{z}}$.
En outre, si $z'\neq0$, $\overline{(\dfrac{z}{z'})}=\overline{z\times\dfrac{1}{z'}}=_{(4)} \overline{z}\times\overline{\dfrac{1}{z'}}=_{\textrm{d'après ci-dessus}}\overline{z}\times \dfrac{1}{\overline{z'}}=\dfrac{\overline{z}}{\overline{z'}}$
Voici un test de six questions à faire en autonomie afin de vérifier votre maîtrise sur les calculs algébriques étudiés depuis le début du chapitre.
Formule du binôme
Coefficients binomiaux
On considère une répétition de $n$ expériences identiques où pour chacune, il n'y a que deux possibilités :
-
soit un succès (noté $S$),
-
soit un échec (noté $E$ ou $\overline{S}$)
Une telle répétition est appelée un schéma de Bernoulli.
On peut représenter cette répétition par un arbre comme ci-dessous où $n=4$ répétitions sont considérées :
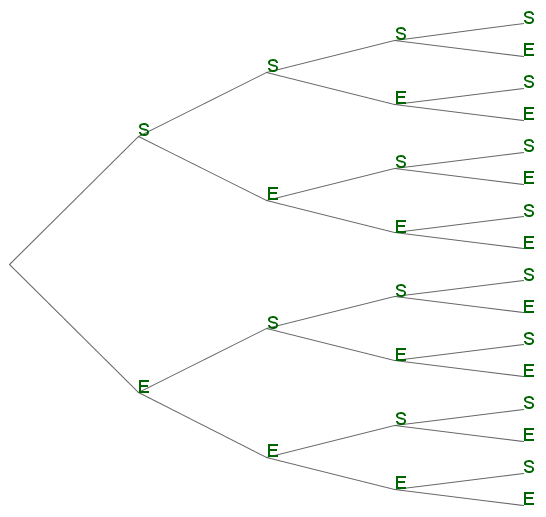
On s'intéresse maintenant aux chemins qui permettent d'avoir un nombre fixe $k$ de succès.
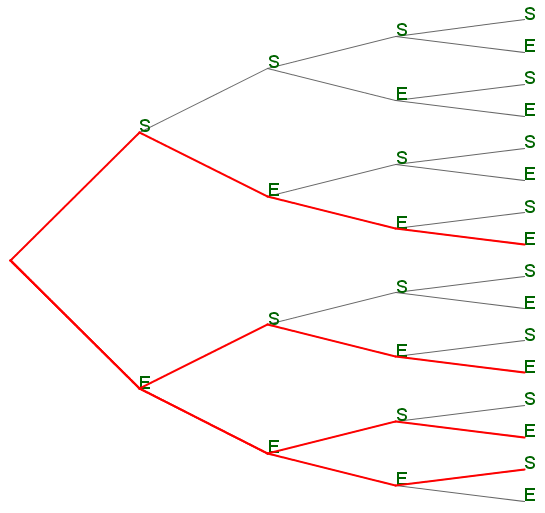
Par exemple, dans l'arbre précédent, si l'on veut obtenir les chemins où l'on ne rencontre que $k=1$ succès sur les $n=4$ répétitions, on obtient l'image suivante :
Soit un schéma de Bernoulli avec $n$ répétitions identiques.
Pour tout entier $0\leq k \leq n$, on appelle coefficient binomial, noté $\displaystyle\binom{n}{k}$, le nombre de chemins du schéma de Bernoulli menant à $k$ succès.
$\displaystyle\binom{n}{k}$ peut être lu "k parmi n".
Par convention $\displaystyle\binom{0}{0}=1$
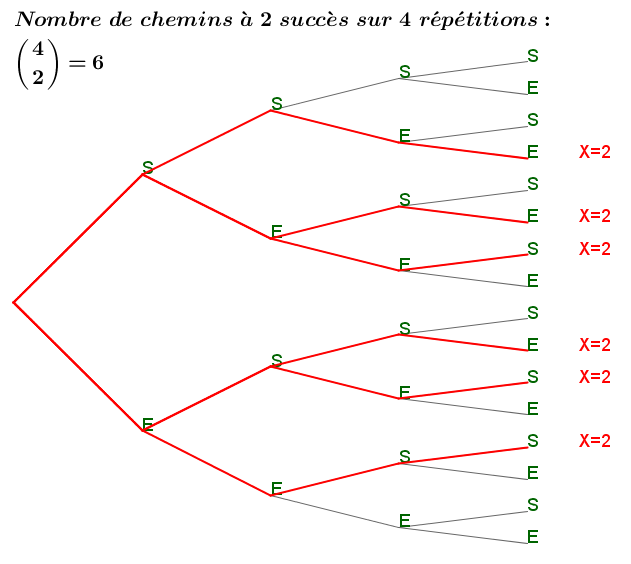
$\displaystyle\binom{4}{2}=6$ : il y a 6 chemins possibles qui conduisent à $k=2$ succès sur $n=4$ répétitions :
-
Dessiner un arbre correspondant à un schéma de Bernoulli dans le cas de 3 répétitions.
-
En déduire les valeurs de $\displaystyle\binom{3}{0}$, $\displaystyle\binom{3}{1}$, $\displaystyle\binom{3}{2}$ et $\displaystyle\binom{3}{3}$.
Vous travaillerez en spécialité maths sur ces coefficients, en particulier, vous démontrerez les propriétés suivantes :
Pour tout entier $k$ et $n$ tels que : $0\leq k \leq n$ :
-
$\displaystyle{\binom{n}{0}=\binom{n}{n}=1}$
-
$\displaystyle{\binom{n}{1}=n}$
-
$\displaystyle{\binom{n}{k}=\binom{n}{n-k}}$
-
$\displaystyle{\binom{n+1}{k+1}=\binom{n}{k}+\binom{n}{k+1}}$
Ces propriétés et les premières valeurs des coefficients binomiaux peuvent être mémorisées grâce au triangle de Pascal :

Compléter le tableau précédent présentant le triangle de Pascal en rajoutant la ligne correspondant à $n=7$.
Vous pouvez trouver une correction vidéo de cet exercice ci-dessous :
Soient $n$ et $k$ deux entiers naturels tels que $ 0\le k \le n$.
Vous verrez aussi en spécialité mathématiques cette année que les coefficients binomiaux peuvent être obtenus par la formule : $\displaystyle \binom{n}{k}=\dfrac{n!}{k! \times (n-k)!}$, où $n! = n\times (n-1) \times ... \times 2 \times 1$ avec la convention $0!=1$.
La formule du binôme de Newton
$a$ et $b$ désigne deux nombres complexes quelconques.
-
Développer l'expression $(a+b)^2$.
-
Développer l'expression $(a+b)^3$.
-
Développer l'expression $(a+b)^4$.
-
Que remarquez-vous quant aux coefficients apparaissant dans le développement de $(a+b)^n$ dans les cas précédant ?
-
Quel développement pouvez-vous conjecturer quant à l'expression $(a+b)^5$ ?
La formule du binôme de Newton :
Quels que soient les nombres complexes $a$ et $b$ et l'entier naturel $n$, on a :
$$\displaystyle (a+b)^n=\sum_{k=0}^{n} \binom{n}{k} a^{n-k}b^k$$
Ce qui peut s'écrire de manière moins condensée en : $\displaystyle (a+b)^n=a^n + \binom{n}{1} a^{n-1}b + \binom{n}{2} a^{n-2}b^2 + ... + \binom{n}{n-2} a^{2}b^{n-2} + \binom{n}{n-1} a b^{n-1} + b^n$.
Voici une démonstration de cette formule du binôme de Newton. Commencer par lire cette démonstration ci-dessous avant de répondre aux questions qui suivent :
On note $P(n)$ la propriété $\displaystyle (a+b)^n=\sum_{k=0}^{n} \binom{n}{k} a^{n-k}b^k$, où $n$ est un entier naturel.
Initialisation :
Pour $n=0$, on a :
D'une part : $(a+b)^0=1$ ;
d'autre part : $\displaystyle \sum_{k=0}^{0} \binom{0}{k} a^{0-k}b^k=\binom{0}{0} \times a^0 \times b^0=1\times 1 \times 1=1$.
Ainsi, $P(0)$ est vraie.
Hérédité :
Considérons un entier $m$ tel que $P(m)$ soit vraie, c'est-à-dire que $\displaystyle (a+b)^m=\sum_{k=0}^{m} \binom{m}{k} a^{m-k}b^k$.
Montrons que $P(m+1)$ est vraie, c'est-à-dire que : $\displaystyle (a+b)^{m+1}=\sum_{k=0}^{m+1}
\binom{m+1}{k} a^{m+1-k}b^k$
Ligne 1 : $\displaystyle (a+b)^{m+1}=(a+b) \times (a+b)^m$
Ligne 2 : $\displaystyle (a+b)^{m+1}=(a+b) \times \sum_{k=0}^{m} \binom{m}{k} a^{m-k}b^k$
Ligne 3 : $\displaystyle (a+b)^{m+1}=\sum_{k=0}^{m} \binom{m}{k} a^{m+1-k}b^k + \sum_{k=0}^{m} \binom{m}{k} a^{m-k}b^{k+1}$
Ligne 4 : $\displaystyle (a+b)^{m+1}=\binom{m}{0} a^{m+1}b^0 + \sum_{k=1}^{m} \binom{m}{k} a^{m+1-k}b^k + \sum_{k=0}^{m-1} \binom{m}{k} a^{m-k}b^{k+1} + \binom{m}{m} a^0 b^{m+1} $
Ligne 5 : $\displaystyle (a+b)^{m+1}=\binom{m}{0} a^{m+1}b^0 + \sum_{k=1}^{m} \binom{m}{k} a^{m+1-k}b^k + \sum_{p=1}^{m} \binom{m}{p-1} a^{m-p+1}b^{p} + \binom{m}{m} a^0 b^{m+1} $
Ligne 6 : $\displaystyle (a+b)^{m+1}=\sum_{k=1}^{m} \binom{m}{k} a^{m+1-k}b^k + \sum_{p=1}^{m} \binom{m}{p-1} a^{m+1-p}b^{p} + a^{m+1} + b^{m+1} $
Ligne 7 : $\displaystyle (a+b)^{m+1}=\sum_{k=1}^{m} \left( \binom{m}{k} + \binom{m}{k-1} \right) a^{m+1-k}b^k + a^{m+1} + b^{m+1} $
Ligne 8 : $\displaystyle (a+b)^{m+1}=a^{m+1} +\sum_{k=1}^{m} \binom{m+1}{k} a^{m+1-k}b^k + b^{m+1} $
Ligne 9 : $\displaystyle (a+b)^{m+1}=\binom{m+1}{0} a^{m+1} +\sum_{k=1}^{m} \binom{m+1}{k} a^{m+1-k}b^k + \binom{m+1}{m+1} b^{m+1} $
Ligne 10 : $\displaystyle (a+b)^{m+1}=\sum_{k=0}^{m+1} \binom{m+1}{k} a^{m+1-k}b^k$
On est donc abouti à $P(m+1)$.
La propriété étant initialisée pour $n=0$ et étant héréditaire, elle est vraie pour tout entier naturel $n$.
-
Quelle idée essentielle sert à cette démonstration et est donc à retenir ?
-
Comment peut-on justifier le passage de la Ligne 1 à la Ligne 2 ?
-
Quelle technique de calcul justifie le passage de la Ligne 2 à la Ligne 3 ?
-
Comment peut-on justifier le passage de la Ligne 3 à la Ligne 4 ?
-
Quel changement de variable permet de justifier le passage de la Ligne 4 à la Ligne 5 ?
-
Quels calculs permettent de justifier le passage de la Ligne 5 à la Ligne 6 ?
-
Expliquer le regroupement des deux termes permettant le passage de la Ligne 6 à la Ligne 7.
-
Comment peut-on justifier le passage de la Ligne 7 à la Ligne 8 ?
-
Quels calculs permettent de justifier le passage de la Ligne 8 à la Ligne 9 ?
-
Comment peut-on justifier le passage de la Ligne 9 à la Ligne 10 ?
Cette formule du binôme était déjà connue de mathématiciens indiens, arabes et persans dès le $X^{e}$ siècle de notre ère. Elle a été démontré au $XIII^{e}$ siècle par le mathématicien chinois Yang Hui indépendamment de ces travaux précédents. En 1665, Issac Newton généralisa cette formule a des exposants non entiers.
Utiliser la formule du binôme de Newton afin de développer puis simplifier les expressions suivantes :
-
$z_1=(3+i)^4$.
-
$z_2=(2i-1)^3$.
$n$ désigne un entier naturel supérieur ou égal à 1.
-
$z$ est un nombre complexe quelconque. Développer $(1+z)^n$.
-
Choisir une valeur adaptée de $z$ afin d'en déduire en fonction de $n$ expression de la somme : $\displaystyle S=\binom{n}{0}+4\binom{n}{1}+4^2 \binom{n}{2}+...+4^n \binom{n}{n}$.
Un petite touche d'humour pour finir sans complexe :
 Merci Flora pour l'idée !
Merci Flora pour l'idée !
Voici un test de quatre questions à faire en autonomie afin de vérifier votre maîtrise sur les coefficients binomiaux et sur la formule du binôme de Newton étudiés depuis le début du chapitre.
Exercices
Calculer avec la forme algébrique
On donne les nombres complexes : $$z_1=-1+2i \textrm{ et } z_2=3+4i.$$ Déterminez la forme algébrique de : $z_1+z_2$, $z_1-z_2$; $2z_1-3z_2$; $z_1\times z_2$.
Donnez la forme algébrique des nombres complexes suivants :
- $(1+i)^2$
- $(1-i)^2$
- $(3-i)^2$
On pose $j=-\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}$.
-
Donnez la forme algébrique de $j^2$.
-
Déterminer le discriminent du polynôme : $X^2+X+1$.
-
Vérifiez que $1+j+j^2=0$.
Donnez la forme algébrique des nombres complexes suivants : $$(2+i)^2(1-3i) \textrm{ et } (5-2i)(1+4i)(2-i).$$
$x$ et $y$ sont deux nombres réels. Quelle est la forme algébrique de $(x+1+iy)(x-1-iy)$.
Manipuler partie réelle et partie imaginaire
On donne les nombres complexes : $$z_1=1-3i\textrm{, } z_2=4+2i \textrm{, }z_3=5-2i.$$
Calculez :
-
$Re(z_1+z_2+z_3)$
-
$Im(iz_1)$
-
$Im(z_1z_2)$
-
$Re(2z_1-3z_2+z_3)$
$z$ est un nombre complexe. Dans chacun des cas suivants, précisez si $Z$ est réel ou imaginaire pur ou ni l'un ni l'autre.
-
$Z=z+\bar{z}-3i$
-
$Z=z-\bar{z}+5i$
-
$Z=z\bar{z}-z+\bar{z}$
-
$Z=\bar{z}(z+i)+i(5i-z)$
Dans chacun des cas suivants, exprimez $\bar{Z}$ en fonction de $\bar{z}$.
-
$Z=-2+iz$
-
$Z=(i+z)(2-iz)$
-
$Z=(2iz+3)^2$
-
$Z=\dfrac{1+iz}{2z-i}$
Déterminer la forme algébrique
Déterminez la forme algébrique de chacun des nombres complexes suivants :
-
$i(1-i)$
-
$(2-3i)(4+i)$
$\dfrac{3+2i}{4-i}$
$\dfrac{1}{2+3i}$
$\dfrac{2}{1+i}-\dfrac{3}{1-i}$
$\dfrac{2+3i}{5-2i}$
$(1+i)(4-3i)(1-i)$
$(3+i)^2(3-2i)$
$\dfrac{2-5i}{3+2i}$
$\dfrac{1}{i\sqrt{2}-3}$
$2i-\dfrac3{2-i}$
On note $z=x+iy$, $x$ et $y$ réels. On pose : $$Z=\dfrac{z-1}{z+1}, z\ne-1$$ Quelle est la forme algébrique de $Z$ ?
Résolvez chacune des équations suivantes :
-
$(3-2i)z=i-2$
-
$(2+i)\bar{z}=3i$
On note $z_1=\dfrac{2i+1}{i+2}$ et $z_2=\dfrac{1-2i}{2-i}$.
-
Pourquoi peut on affirmer sans calcul que $z_1+z_2$ est réel et $z_1-z_2$ imaginaire pur?
-
Retrouvez ces résultats par le calcul.
Proposer une fonction écrite en langage Python qui :
-
prend quatre paramètres : les parties réelle et imaginaire de deux nombres complexes $z_1$ et $z_2$.
-
retourne la partie réelle et imaginaire du quotient $\dfrac{z_1}{z_2}$ quand il existe et la chaîne de caractères "le quotient n'existe pas" sinon.
Résolution d'équation
Résolvez dans $\mathbb{C}$ les équations suivantes et donnez les résultats sous forme algébrique.
-
$3iz-2+4i=(1-2i)z+6$
$(3+2i)z=2i\bar{z}-5i$
$\dfrac{z+1}{z-1}=i$
$(2iz+i)(4z-8-4i)=0$
$4\bar{z}+2i-4=0$
Résolvez dans $\mathbb{C}$ les équations suivantes et donnez les résultats sous forme algébrique.
-
$iz-2\overline{z}=\overline{i}$
$\left(\overline{z-4i}+2\right)(z+2i)=0$
$\displaystyle \dfrac{z+i}{\overline{z-2}-2i}=\dfrac{2-i}{3}$
$\dfrac{\overline{2iz+5}}{z+2i}=2+3i$.
$(3-2i)z=4(\overline{z+i})$
$3z+4i=(3-z)(1+2i)$
Binôme de Newton
Développer les expressions suivantes à l'aide du binôme de Newton et du triangle de Pascal :
-
$(3z+2i)^5$.
$\left(\dfrac{1}{2} z+2\right)^4$.
Quel est le coefficient de $z^4$ dans le développement de $(2z+1)^8$ ?
On considère les deux sommes suivantes :
$$A=\displaystyle \sum_{k=0}^{50} \binom{100}{2 \times k} = \binom{100}{0} + \binom{100}{2} + \binom{100}{4} + ... + \binom{100}{98} + \binom{100}{100}$$ $$B=\displaystyle \sum_{k=0}^{49} \binom{100}{2 \times k +1} = \binom{100}{1} + \binom{100}{3} + \binom{100}{5} + ... + \binom{100}{97} + \binom{100}{99}$$-
Développer l'expression $(x+1)^n$ en utilisant la formule du binôme de Newton.
-
Calculer la somme $A+B$, sans chercher à connaître ni $A$, ni $B$.
-
De même, calculer la différence $A-B$.
-
En déduire les valeurs de $A$ et de $B$.
Utilisation de Python
Pour tester des codes en langage Python, vous pouvez utiliser Edupython ou directement le site trinket.
Découverte de quelques instructions natives en Python
-
Tester les instructions suivantes dans la partie console et comprendre le rôle de chacune :
-
>>> z1 = complex(4, 7) >>>z1 -
>>> z1.conjugate() -
>>> z1.real -
>>> z1.imag -
>>> z2 = complex(1, -3) >>>z2 -
>>> z1+z2 -
>>> z1/z2 -
>>> z2**5
-
-
Quelles remarques peut-on faire sur l'affichage sous Python d'un nombre complexe écrit sous forme algébrique ?
Utilisation de quelques instructions en Python
On considère les nombres entiers $n$ compris entre -10 et 10.
On souhaite déterminer pour quelles valeurs de $n$ le nombre complexe $(3n+i)(-75+in)$ est un nombre réel.
-
Compléter la fonction
solutionci-dessous afin qu'elle renvoie la listeL, qui contiendra la liste des entiers $n$ compris entre -10 et 10 qui correspondent au problème.def solution(): L = [] for ......Pour ajouter un élément
eltà la fin d'une listeliste, il suffit d'utiliser la méthodeappendavec le script :liste.append(elt) -
Utilisez Edupython (ou le Trinket ci-dessous) pour tester la fonction complétée et donner les valeurs de $n$ qui semblent convenir.
-
Retrouver le résultat algébriquement.
On considère la fonction developper ci-dessous :
def developper(a,b):
S = 0
L = [1, 4, 6, 4, 1]
for k in range(5):
S = S + L[k] * a**k * b**(4-k)
return S -
-
Que représente les termes de la liste
L? -
Déterminer l'expression de
Sen fonction de $a$ et de $b$. -
Quelle valeur renvoie la fonction pour $a=1$ et $b=i$ ?
-
-
Ilane a testé la fonction et a obtenu le résultat suivant :
>>>developper(5, complex(0, 3)) (-644+960j)Quelle égalité mathématique peut-elle écrire ?
Synthèse
Une suite complexe qui aime l'arithmétique.
On considère la suite $(z_n)$ définie par $\left\{ \begin{array}{l} z_0=0\\ z_{n+1}=i z_n-4 \textrm{, pour tout } n\in\mathbb{N} \end{array} \right.$
-
Déterminer la forme algébrique de $z_1$ , $z_2$ et $z_3$.
-
Pour tout entier naturel $n$, on pose $z_n=a_n+ib_n$ où $a_n$ est la partie réelle de $z_n$ et $b_n$ la partie imaginaire de $z_n$.
-
Donner la valeur de $a_0$, $b_0$, $a_1$, $b_1$, $a_2$, $b_2$.
-
Soit $n\in\mathbb{N}$, exprimer $a_{n+1}$ et $b_{n+1}$ en fonction de $a_n$ et $b_n$.
-
Compléter le script de la fonction
z. L'appelz(50)doit renvoyer un couple de valeurs correspondant à $a_{50}$ et $b_{50}$, les termes d'indice $50$ des suites $(a_n)$ et $(b_n)$.def z(n): """ n : de type entier renvoie un couple de valeurs correspondant à la partie réelle et imaginaire du terme d'indice n de la suite z """ a = ... b = ... for i in range(...): ... return a, b print(z(...))Pour rappel :
-
L'instruction
for i in range(5):permettra à i de prendre les valeurs de 0 à 4. En fait 5 valeurs, en commençant par 0 et en incrémentant de 1. -
Le test d'égalité
a == brenvoieTruesi le contenu des variablesaetbsont égaux etFalsesinon. -
val = complex(4, -5)permet d'implémenter en Python le nombre complexe $4-5i$ puis de stocker cette valeur dans une variableval.
-
-
Que peut-on dire des termes de la suite $(z_n)$?
-
-
Montrer que pour tout $n\in\mathbb{N}$, $z_n=(2+2i)i^n-2-2i$.
-
Démontrer l'affirmation faite en 2.d.
Vous pouvez utilisez le site trinket pour tester votre script.
Les nombres complexes sont très utiles dans l'étude de phénomènes électriques. Le physicien britannique Heaviside a introduit la notion d'impédance en 1886 qui permet de généraliser la loi d'Ohm $U=RI$ du courant continue en $\underline{U}=\underline{Z}\times\underline{I}$ qui correspond au cas alternatif. Dans cette formule, $\underline{U}$, $\underline{I}$ sont des nombres complexes représentant la tension et l'intensité d'un composant ou d'un circuit, tandis que $\underline{Z}$ est l'impédance du composant ou du circuit.
Le quadripôle représentée ci-dessous est constitué d'un résistor de résistance $R$, en $\Omega$, et d'un condensateur de capacité $C$, en $\mu F$.
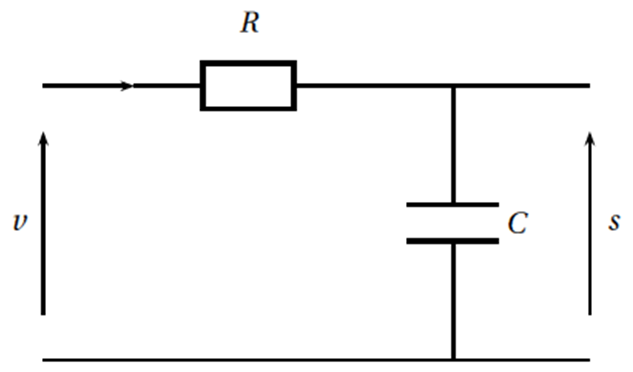
On associe respectivement à la tension d'entrée et à la tension de sortie les nombres complexes $v$ et $s$. On appelle transmittance le nombre complexe $Z$ défini par $Z=\dfrac{s}{v}$.
On admet que $\displaystyle Z=\dfrac{1}{1+jRC\omega}$, où $\omega$ désigne la pulsation exprimée en radian par seconde et $j$ un nombre complexe tel que $j^2=-1$.
On suppose dans cet exercice que : $R=50 \Omega$, $C=2 \mu F$ et $\omega=\dfrac{1}{100} rad.s^{-1}$.
-
Déterminer la forme algébrique de $Z$.
-
On suppose que $v=150(-\sqrt{3}+j)$. Déterminer la forme algébrique de $s$.
On a prolongé dans $\mathbb{C}$ l'addition et la multiplication que vous pratiquiez déjà avec des nombres réels.
En utilisant le produit $i \times i$, expliquez pourquoi on ne peut pas comparer des nombres complexes comme on le fait dans $\mathbb{R}$ en restant compatible avec l'addition et la multiplication.
On considère le nombre $j=\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i$ et un entier naturel $n$.
On souhaite étudier les nombres $j^n$.
-
Calculer les valeurs de $j^2$, $j^3$ et $j^4$.
-
-
Compléter la fonction suivante afin qu'elle renvoie la liste des entiers positifs $m$ inférieurs ou égaux à un entier $n$ tels que le nombre $j^m$ soit réel.
from math import sqrt def liste_reel(n): j = complex(sqrt(2)/2,sqrt(2)/2) L = [] for ......................... ... ... return L-
Pour rajouter un élément
elten fin d'une listeliste, il suffit de saisir en Pythonliste.append(elt). -
N'hésitez pas à utiliser les méthodes sur les nombres complexes vues à l'exercice 39.
-
Du fait de la présence du nombre irrationnel $\sqrt{2}$, le moteur Python travaillera avec une valeur approchée de $\sqrt{2}$ et non la valeur exacte.
Dès lors un test d'égalité avec 0 n'a pas de sens.
Plutôt qu'un test du typea == 0, il faudra préférer un test d'approximation du typea<=0.0000000001 and a>=-0.0000000001.
-
-
Tester la fonction pour $n=10$, puis pour $n=20$, enfin pour d'autres valeurs de $n$.
-
Que peut-on conjecturer quant aux valeurs de $n$ pour lesquelles $j^n$ est un nombre réel ?
-
-
-
Recopier et compléter le tableau suivant après avoir calculé la forme algébrique de $j^n$ correspondante :
Valeur de $n$ 0 1 2 3 4 5 6 7 8 Forme algébrique de $j^n$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ -
Démontrer que, pour tout entier naturel $n$, $j^{n+8}=j^n$.
-
Démontrer la conjecture émise à la question 2.c.
-
-
Déterminer pour quelles valeurs de $n$, le nombre $j^n$ est un imaginaire pur.
-
-
À l'aide de la formule du binôme de Newton, démontrer l'égalité : $\displaystyle j^n=\left(\dfrac{\sqrt{2}}{2}\right)^{n} \times \sum_{k=0}^{n}\binom{n}{k} i^k$.
-
En déduire que pour tout entier naturel $n$ : $\displaystyle \sum_{k=0}^{8n}\binom{8n}{k} i^k= 16^{n}$.
-
En déduire la valeur exacte de : $\displaystyle \sum_{k=0}^{2024}\binom{2024}{k} i^k$.
-
Soit $a$ un nombre complexe non nul et différent de 0.
On définit la suite $(z_n)$ de nombres complexes par $z_0=0$ et,
pour tout entier naturel $n$, $z_{n+1}=a\times z_n-i$.
-
-
Exprimer les nombres complexes $z_1$, $z_2$ et $z_3$ en fonction du nombre complexe $a$.
-
Démontrer par récurrence que pour tout entier naturel $n$, $z_n=\dfrac{1-a^n}{a-1}\times i$.
-
-
Dans cette question 2. uniquement, on suppose que $a=1+i$.
-
Démontrer en utilisant la formule du binôme de Newton que, pour tout entier naturel $n$, $\displaystyle z_n=1-\sum_{k=0}^{n} \binom{n}{k} i^k$.
-
Soit $p$ un entier naturel.
En calculant de deux manières différentes $(1+i)^{4p}$, démontrer que $\displaystyle \sum_{k=0}^{4p} \binom{4p}{k} i^k=(-4)^{p}$.
-
-
-
Compléter la fonction suivante afin qu'elle renvoie la liste des termes de la suite $(z_n)$ lorsque $n$ est compris entre $0$ et $m$.
def liste_termes(m): i = complex(0, 1) z = 0 liste = [] for ......................... ... ... return liste-
Pour rajouter un élément
elten fin d'une listeliste, il suffit de saisir en Pythonliste.append(elt). -
N'hésitez pas à utiliser les méthodes sur les nombres complexes vues à l'exercice 39.
-
Vérifier le bon fonctionnement de la fonction complétée en vérifiant que
liste_termes(3)renvoie bien[0j, -1j, (1-1j), (1+0j)].
-
-
Tester la fonction pour $m=10$, puis pour $m=20$.
-
Quelle conjecture pouvez-vous énoncer quant aux valeurs des termes de la suite $(z_n)$ ?
-
-
-
Calculer à la main la valeurs des nombres complexes $z_1$, $z_2$, $z_3$ et $z_4$.
-
Démontrer que, pour tout entier naturel $n$, $z_{n+4}=z_n$.
-
-
On munit le plan d'un repère orthonormal $(O\ ; \overrightarrow{u}, \overrightarrow{v})$.
On pose, pour tout entier naturel $n$, $z_n = x_n+i y_n$, où $x_n=Re(z_n)$ et $y_n=Im(z_n)$.
On appelle $P_n$ les points de coordonnées $(x_n ; y_n)$.
Placer les points $P_0$ à $P_7$ dans le repère, puis le point $P_{2025}$ en justifiant la position de ce dernier point.
Dans toute la suite, on travaille avec comme nombre complexe particulier $a=i$.
On dit qu'un entier naturel $N$ est somme de deux carrés s'il existe deux entiers naturels $a$ et $b$ tels que $N=a^2+b^2$.
-
Proposer une fonction nommée
est_carrequi permet de savoir si un entier naturel $N$ est somme deux carrés ; cette fonction renverra le booléenTruedans le cas où l'argument $N$ saisi est bien un carré de deux entiers etFalsesinon. -
-
Comment écrire $N_1$ et $N_2$ en fonction de $z_1$ et de $z_2$ ?
-
En déduire que $N_1 N_2$ est somme de deux carrés.
On souhaite prouver que, si $N_1$ et $N_2$ sont somme de deux carrés alors leur produit $N_1 N_2$ est aussi somme de deux carrés.
Pour cela, on écrit $N_1=a^2+b^2$ et $N_2=c^2+d^2$ et on introduit $z_1=a+ib$ et $z_2=c+id$.
-
-
Démontrer que si $N$ est somme de deux carrés, alors pour tout entier $p\geq 1$, $N^p$ est aussi somme de deux carrés.
QCM : Donner la seule réponse exacte parmi les trois proposées
-
Soit $n\in \mathbb{N}$, le nombre complexe $\displaystyle \left(\sqrt{3} +i \right)^n$ est un imaginaire pur si et seulement si :
-
$n=3$
-
$n=6k+3, k\in \mathbb{N}$
-
$n=6k, k\in \mathbb{N}$
-
-
Une solution de l'équation $2z+\overline{z}=9+i$ est
-
3
-
$i$
-
$3+i$
-
-
L'ensemble des solutions dans $\mathbb{C}$ de l'équation $\displaystyle \dfrac{z-2}{z-1}=z$ est :
-
$S=\{1+i\}$
-
$S=\varnothing$
-
$S=\{1-i;1+i\}$
-
-
La partie réelle du nombre $(2+5i)^3$ est :
-
8
-
-142
-
68
-
-
L'ensemble des solutions dans $\mathbb{C}$ de l'équation $z-\overline{z}+2-4i=0$ est :
-
le nombre $2i$
-
l'ensemble des nombres $x+2i$ avec $x\in\mathbb{R}$
-
l'ensemble vide.
-
Lors d'une réception d'un signal émis par un satellite, il apparaît une perte d'anergie dues aux impédances de la parabole et du câble coaxial.
On mesure cette perte par le coefficient de réflexion $R$ défini par $R=\dfrac{z-z'}{z+z'}$, où $z$ est l'impédance complexe de la parabole et $z'$ l'impédance complexe du câble coaxial.
Lorsque $R$ s'écrit sous la forme algébrique $a+ib$, on définit $p=\sqrt{a^2+b^2}$.
-
-
Montrer que si une installation fournit comme impédances $z=75$ et $z'=46.6-20.3i$, alors on obtient $p=0.28$.
Le Rapport d'Onde Stationnaire ($ROS$) est défini par le rapport : $ROS=\dfrac{1+p}{1-p}$. Calculer le $ROS$ pour cette installation.
Pour respecter la norme imposée, le $RSO$ doit être inférieur à 2. L'installation est-elle conforme ?
-
-
Dans le cas général, pour toute installation, on admet que $p$ est compris entre 0 et 1. Quelle est la valeur maximum de $p$ qui respecte la norme imposée ?
On considère le nombre $j=\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i$ et un entier naturel $n$.
On souhaite étudier les nombres $j^n$.
-
Calculer les valeurs de $j^2$, $j^3$ et de $j^4$.
-
-
Compléter la fonction suivante afin qu'elle renvoie la liste des entiers positifs $m$ inférieurs ou égaux à un entier $n$ tels que le nombre $j^m$ soit réel.
from math import sqrt def liste_reel(n): j = complex(1/2,-sqrt(3)/2) L = [] for ......................... ... ... return L-
Pour rajouter un élément
elten fin d'une listeliste, il suffit de saisir en Pythonliste.append(elt). -
N'hésitez pas à utiliser les méthodes sur les nombres complexes vues à l'exercice 39.
-
Du fait de la présence du nombre irrationnel $\sqrt{3}$, le moteur Python travaillera avec une valeur approchée de $\sqrt{3}$ et non la valeur exacte.
Dès lors un test d'égalité avec 0 n'a pas de sens.
Plutôt qu'un test du typea == 0, il faudra préférer un test d'approximation du typea<=0.0000000001 and a>=-0.0000000001.
-
-
Tester la fonction pour $n=20$, puis pour $n=40$, enfin pour d'autres valeurs de $n$.
-
Que peut-on conjecturer quant aux valeurs de $n$ pour lesquelles $j^n$ est un nombre réel ?
-
-
-
Recopier et compléter le tableau suivant après avoir calculé la forme algébrique de $j^n$ correspondante :
Valeur de $n$ 0 1 2 3 4 5 6 Forme algébrique de $j^n$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ -
Démontrer que, pour tout entier naturel $n$, $j^{n+6}=j^n$.
-
En déduire la valeur exacte de $j^{2023}$.
-
Démontrer la conjecture émise à la question 2.c.
-
-
-
À l'aide de la formule du binôme de Newton, démontrer l'égalité : $\displaystyle j^n=\left(\dfrac{1}{2}\right)^{n} \times \sum_{k=0}^{n}\binom{n}{k} \left(-\sqrt{3}i\right)^k$.
-
En déduire que pour tout entier naturel $p$ : $\displaystyle \sum_{k=0}^{6p}\binom{6p}{k} \left(-\sqrt{3}i\right)^k = 64^{p}$.
-
Savoirs et savoirs-faire
-
la forme algébrique d'un nombre complexe,
-
la notion de partie réelle et de partie imaginaire,
-
la notion de conjugué d'un nombre complexe,
-
la formule du binôme de Newton.
-
refaire la démonstration du conjugué d'un produit,
-
refaire la démonstration du conjugué d'un inverse,
-
refaire la démonstration du conjugué d'une puissance entière,
-
refaire la démonstration de la formule du binôme de Newton.
-
calculer (additionner, multiplier, diviser) avec des nombres complexes,
-
résoudre des équations du premier degré avec des nombres complexes,
-
résoudre une équation simple faisant intervenir $z$ et $\overline{z}$,
-
utiliser la formule du binôme de Newton pour développer une puissance.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International