Demander le programme !

Voici une frise historique présentant les premiers mathématiciens qui ont travaillé sur la représentation et l'interprétation géométrique des nombres complexes.

Représentation géométrique.
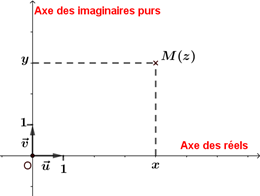
Affixe d'un point
- On appelle plan complexe le plan muni d'un repère orthonormé $(0 ; \vec{u},\vec{v})$.
- A tout nombre complexe $z=x+iy$ avec $x$ et $y$ nombres réels, on associe le point $M$ de coordonnées $(x ; y)$.
- Réciproquement, à tout point $M(x ; y)$ du plan complexe, on associe le nombre complexe $z=x+iy$.
On dit que le point $M$ est le point image du nombre complexe $z$ et que $z$ est l'affixe du point $M$.
- Le point $E(-2 ; 3)$ a pour affixe $-2+3i$.
- Le point image du nombre complexe $1-i$ est le point $F(1 ; -1)$.
Notation et vocabulaire
|
 |
|  |
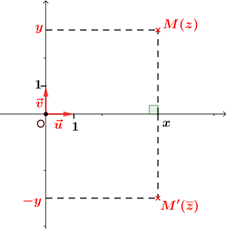
Interprétation géométrique du conjugué
|
Le point $M$ d'affixe $z$ et le point $M'$ d'affixe $\overline{z}$ En effet si $z = x+iy $ $(x\in\mathbb{R} \textrm{ et } y\in\mathbb{R})$, alors $\overline{z}=x-iy$, donc $M$ et $M'$ ont la même abscisse et des ordonnées opposées. |
 |
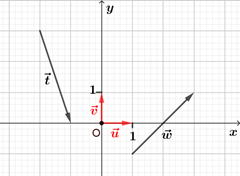
Affixe d'un vecteur
|
Dans le plan complexe, $\vec{w}$ est un vecteur de coordonnées $(x ; y)$. Le point $M$ tel que $\overrightarrow{OM} = \vec{w}$ a pour coordonnées $(x ; y)$, donc le vecteur $\overrightarrow{OM}$ a pour affixe $x+iy$. On dit que le vecteur $\vec{w}$ est le vecteur image du nombre complexe $z$ et que $z$ est l'affixe du vecteur $\vec{w}$. | 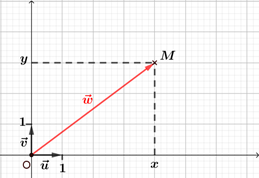 |
|
Soit $M$ un point du plan complexe muni d'un repère d'origine $O$ et $z$ un nombre complexe. Le point $M$ a pour affixe $z$ si, seulement si le vecteur $\overrightarrow{OM}$ a pour affixe $z$. | 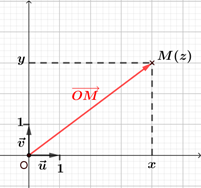 |
l'affixe du point $O$ l'origine d'un repère du plan complexe est $0$.
l'affixe du vecteur nul $\vec0$ est $0$.
|  |
Propriétés
En utilisant les propriétés des coordonnées, on déduit les propriétés suivantes
Dans le plan complexe, on considère les vecteurs $\vec{w}$ et $\vec{w'}$ d'affixes respectives $z$ et $z'$ et $k$ un réel.
-
Les vecteurs $\vec{w}$ et $\vec{w'}$ sont égaux si, et seulement $z$ = $z'$.
-
Le vecteur $\vec{w}+\vec{w'}$ a pour affixe $z + z'$.
-
Le vecteur $k\vec{w}$ a pour affixe $kz$.
-
L'affixe du vecteur $\overrightarrow{AB}$ est le nombre complexe $z_A-z_B$.
-
L'affixe du milieu $I$ du segment $[AB]$ est le nombre complexe $z_I=\dfrac{z_A+z_B}{2}$.
Soient $A$ et $B$ deux points du plan complexe d'affixes respectives $z_A$ et $z_B$.
Ces 2 propriétés découlent directement des propriétés sur les coordonnées des vecteurs et du milieu d'un segement :
On sait que $\overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA}$, donc $z_\overrightarrow{AB} = z_{\overrightarrow{OB}}-z_{\overrightarrow{OA}}$, Or, $z_\overrightarrow{OA} = z_A$ et $z_\overrightarrow{OB} = z_B$, Ainsi, $z_\overrightarrow{AB} = z_A-z_B$.
Soit $I$ le milieu du segment $[AB]$, alors :
$\overrightarrow{AI} = \overrightarrow{IB}$, donc $z_\overrightarrow{AI} = z_\overrightarrow{IB}$ soit $z_I-z_A = z_B-z_I$, ainsi $2z_I=z_B+z_A$, par conséquent, $z_I=\dfrac{z_A+z_B}{2}$
Dans le plan complexe on donne les points $A$, $B$, $C$ et $D$ d'affixes : $z_A=-3-i$, $z_B=1+i$ $z_C=3-2i$ et $z_D=-1-4i$.
- Placer les points $A$, $B$, $C$ et $D$ dans le plan complexe en utilisant la figure ci-dessous. Que peut-on dire des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ ?
- Déterminer les affixes des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$
- En déduire la nature du quadrilatère ABCD.
Dans le plan complexe on donne les points par leurs affixes $A(1)$, $B(-2 – i)$ et $C(4i)$
- Déterminer l’affixe du point D tel que ABCD soit un parallélogramme.
- Déterminer l’affixe du point $M$, centre du parallélogramme ABCD.
Dans le plan complexe on donne les points $A$, $B$ et $C$ d'affixes : $z_A=-3+5i$, $z_B=-1+i$ et $z_C=-i$.
- Placer les points $A$, $B$ et $C$ dans le plan complexe en utilisant la figure ci-dessous et émettre une conjecture.
- Démontrer ou invalider cette conjecture.
Dans le plan complexe, on note $\mathcal{E}$, l'ensemble des points $M$ d'affixe $z$ tels que $Z=z^2$ soit un réel.
Déterminer l'ensemble $\mathcal{E}$, puis le représenter graphiquement dans un repère orthonormé $(0 ; \vec{u},\vec{v})$.
Module d'un nombre complexe
$(0 ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexe.
Définitions et propriétés
|
Soit $M$ le point d'affixe $z$. Le module de $z$ , noté $| z |$ , est la distance $OM$, c'est-à-dire $| z | = OM$. | 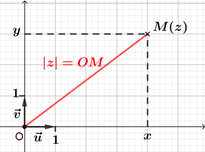 |
|
Pour tout nombre complexe $z$ de forme algébrique $x+iy$ $(x\in\mathbb{R} \textrm{ et } y\in\mathbb{R})$.
|  |
Soient $z$ un nombre complexe de forme algébrique $x+iy$ $(x\in\mathbb{R} \textrm{ et } y\in\mathbb{R})$ et $M(x ; y)$ son point d'image, alors,
$|z| = OM = \sqrt{(x_M-x_O)^2 + (y_M-y_O)^2}=\sqrt{(x-0)^2 + (y-0)^2}=\sqrt{x^2+y^2}$.
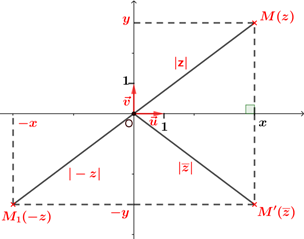
$-z = -x+i(-y)$, donc $|-z| =\sqrt{(-x)^2+(-y)^2}=\sqrt{x^2+y^2}=|z|$
$\overline{z} = x+i(-y)$, donc $|\overline{z}| =\sqrt{x^2+(-y)^2}=\sqrt{x^2+y^2}=|z|$.
$z\overline{z} = (x+iy)(x-iy) = x^2+y^2 =(\sqrt{x^2+y^2})^2=|z|^2 $.
- Si $x$ est un nombre réel, le module de $x$ est égal à la valeur absolue de $x$.
- $|z|=0$ équivaut à $z=0$ car $OM=0$ équivaut à $M=O$.
Soient $A$ et $B$ deux points du plan complexe d'affixes respectives $z_A$ et $z_B$.
$AB=|z_A-z_B|$.
Soient $A(x_A ; y_A)$ et $B(x_B ; y_B)$ deux points du plan complexe, alors, $z_A=x_A +iy_A$ et $z_B=x_B +iy_B$.
On sait que $AB = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}$,
et $z_B-z_A=x_B +iy_B-(x_A +iy_A) = (x_B-x_A)+i(y_B-y_A)$, donc, $|z_B-z_A|=\sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}=AB$
- Dans le plan complexes, placer les points $A(6-3i)$, $B(15+2i)$ et $C(18-3i)$.
- Que peut-on conjecturer quant à la nature du triangle $ABC$ ?
- Démontrer ou invalider cette conjecture.
- Dans le plan complexes, placer les points $D(2-i)$, $E(6-i)$ et $F\left(4+(2\sqrt{3}-1)i\right)$.
- Montrer que le triangle $DEF$ est équilatéral.
- Calculer l'aire du triangle $DEF$.
Pour tous nombres complexes $z$, $z'$ et tout nombre entier naturel $n\ge 1$.
-
$|zz'| = |z|\times|z'|$
-
$|z^n| = |z|^n$
-
$\left\lvert\dfrac{1}{z'}\right\rvert = \dfrac{1}{|z'|}$, si $z'\ne0$.
-
$\left\lvert\dfrac{z}{z'}\right\rvert = \dfrac{|z|}{|z'|}$, si $z'\ne0$
- $|zz'|^2 = zz'\times\overline{zz'}=z\overline{z}\times z'\overline{z'} = |z|^2\times|z'|^2 =(|z||z'|)^2 $. Or, $|zz'|$ et $|z||z'|$ sont deux réels positifs, donc $|zz'|=|z||z'|$
- Montrons par récurrence que pour tout entier $n\ge 1$, $|z^n| = |z|^n$ :
- Pour $n=1$, $|z^1|=|z|=|z|^1$
- Soit $k \in \mathbb{N}$ avec $k\ge 1$, supposons que $|z^k| = |z|^k$ et montrons que $|z^{k+1}| = |z|^{k+1}$ :
Or, $|z^{k+1}|=|z^k\times z| = |z^k|\times |z| = |z|^k\times |z| = |z|^{k+1}$.
- Ainsi, pour tout entier $n\ge 1$, $|z^n| = |z|^n$.
Soient $z$ et $z'$ deux nombres complexes avec $z'\ne0$ :
Alors, $z'\times\dfrac{1}{z'} = 1$, donc $\left\lvert z'\times\dfrac{1}{z'}\right\rvert = 1$, soit $|z'|\times\left\lvert\dfrac{1}{z'}\right\rvert = 1$, ainsi, $\left\lvert\dfrac{1}{z'}\right\rvert = \dfrac{1}{|z'|}$.
Soient $z$ et $z'$ deux nombres complexes avec $z'\ne0$.
Alors, $\left\lvert\dfrac{z}{z'}\right\rvert=\left\lvert z\times\dfrac{1}{z'}\right\rvert = |z|\times\left\lvert\dfrac{1}{z'}\right\rvert = |z|\times\dfrac{1}{|z'|} = \dfrac{|z|}{|z'|}$.
- Calculer le module de chacun des nombres complexes $\sqrt{3}+i$ et $1-2i$.
Déterminer alors le module de chaque nombre complexe :
$z_1=(\sqrt{3}+i)(1-2i)$, $z_2=(\sqrt{3}+i)^3$, $z_3=\dfrac{1}{1-2i}$ et $z_4=\dfrac{\sqrt{3}+i}{1-2i}$.
- On donne les points $A$ et $B$ d'affixes $z_A=2+5i$ et $z_B=-3i$.
$M$ désigne un point du plan complexe d'affixe $z$.
- Déterminer les affixes des vecterus $\overrightarrow{AM}$, et $\overrightarrow{BM}$
- Déterminer l'ensemble $\mathscr{E}$ des points $M$ tel que : $|z-2-5i|=|z+3i|$
- Le plan complexe est muni d'un repère orthonormé direct $(O;\vec{u},\vec{v})$. On donne le point $A$ d'affixe $1-i$.
$M$ est un point d'affixe $z$. Déterminer l'affixe du vecteur $\overrightarrow{AM}$.
Déterminer l'ensemble $\mathscr{F}$ des points $M$ du plan dont l'affixe vérifie $|z-1+i|=2$
Ensemble $\mathbb{U}$ des nombres complexes de module $1$
|
On note $\mathbb{U}$ l'ensemble es nombres complexes $z$ tels que $|z|=1$. Dans le plan complexe, $\mathbb{U}$ est représenté par le cercle de centre $O$ et de rayon $1$. | 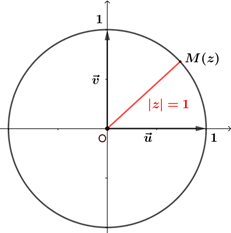 |
Pour tous nombres complexes $z$ et $z'$ de l'ensemble $\mathbb{U}$ :
- $zz' \in \mathbb{U}$.
- $\dfrac{1}{z} \in \mathbb{U}$.
- $|zz'|=|z||z'|$, or $|z|=|z'|=1$, donc $|zz'|= 1$ et $zz'$ appartient à $\mathbb{U}$.
- $\left\lvert\dfrac{1}{z}\right\rvert = \dfrac{1}{|z|}$, or, $|z|=1$, donc, $\left\lvert\dfrac{1}{z}\right\rvert =1$ et $\dfrac{1}{z} \in \mathbb{U}$.
Soient $z$ et $z'$ deux nombres complexes de l'ensemble $\mathbb{U}$ :
On considère le nombre complexe $j=-\dfrac{1}{2}+i\dfrac{\sqrt3}{2}$.
- Donner une forme algébrique de $j^2$ et $j^3$
- Varifier que ces nombres complexes appartiennent à \mathbb{U}.
- Calculer $j+j^2+j^3$
- Placer ces points dans le plan complexes en utilisant la figure ci-dessous.
- Démontrer que le triangle PQR est équilatéral.
Arguments d'un nombre complexe
$(O ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexe.
$\mathscr{C}$ est le cercle trigonométrique de centre $O$.
Définition et interprétation géométrique
|
Soit $z$ un nombre complexe non nul de point image $M$ du plan complexe, $N$ est le point d'intersection du cercle trigonométrique $\mathscr{C}$ et de la demi-droite $[OM)$. On appelle argument de $z$ et on note arg(z) tout nombre $\theta$ dont le point $N$ est l'image sur le cercle trigonométrique $\mathscr{C}$. | 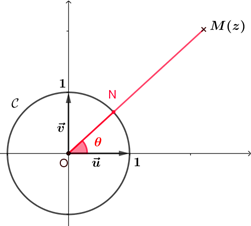 |
Un nombre complexe non nul a une infinité d'arguments. Si $\theta$ est un argument d'un nombre complexe $z$, tous les autres sont de la forme $\theta+2k\pi$ avec $k\in \mathbb{Z}$. On note $\theta = arg(z) ~[2\pi]$ et on lit "$\theta$ égal argument de $z$ modulo $2\pi$"
L'argument appartenant à $]-\pi ; \pi[$ est appelé argument principal de $z$
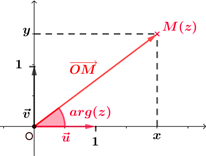
Interprétation géométrique
|
On se place dans un plan complexe muni d'un repère orthonormé direct $(O ; \vec{u},\vec{v})$.
|  |
Cette propriété est une conséquence directe de la définition.
Le nombre complexe $0$ est le seul nombre complexe qui n'a pas d'argument.
- Dans le plan complexe, placer les points A, B, C, D d'affixes respectives $1+i$, $-1-i$, $1-i$, $-1+i$.
- Lire graphiquement un argument de chacun de ces nombres complexes.
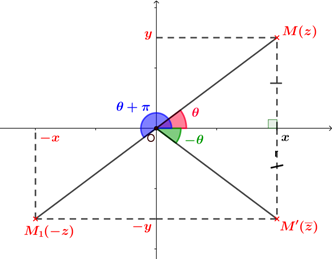
Premières propriétés des arguments
|
Pour tout nombre complexe non nul $z$ et tout réel $k$ non nul :
|  |
Cette propriété est une conséquence directe des propriétés des mesures des angles orientés.
|
Soient $A$ et $B$ deux points distincts d'affixes respectives $z_A$ et $z_B$. On a $\left(\vec{u} ; \overrightarrow{AB}\right)=arg(z_B-z_A) ~[2\pi]$. | 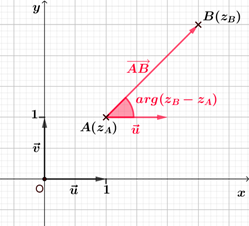 |
|
Soient $A$ et $B$ deux points distincts d'affixes respectives $z_A$ et $z_B$. On note $M$ le point tel que $\overrightarrow{OM}=\overrightarrow{AB}$ et $z_M$ l'affixe de ce point. Alors, $z_M-z_O=z_B-z_A$, soit $z_M=z_B-z_A$. De plus, $\left(\vec{u} ; \overrightarrow{OM}\right)=arg(z_M) ~[2\pi]$ soit, $\left(\vec{u} ; \overrightarrow{OM}\right)=arg(z_B-z_A) ~[2\pi]$. Or, $\left(\vec{u} ; \overrightarrow{OM}\right)=\left(\vec{u} ; \overrightarrow{AB}\right)$, donc $\left(\vec{u} ; \overrightarrow{AB}\right)=arg(z_B-z_A) ~[2\pi]$. | 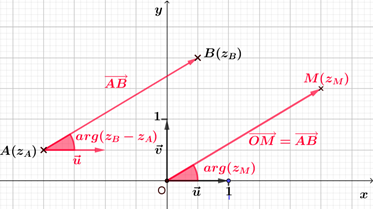 |
Soit $z$ un nombre complexe non nul de forme algébrique $x+iy$ ($x$ et $y$ réels).
- Alors un argument de $z$ est un réel $\theta$ tel que $\left\{ \begin{array}{l!l} cos(\theta)=&\dfrac{x}{|z|}\\[3pt] sin(\theta)=&\dfrac{y}{|z|} \end{array}\right.$
|
Soit $z=x+iy$ ($x\in\mathbb{R}$ et $y\in\mathbb{R}$) un nombre complexe non nul dont un argument est $\theta$. $M$ est le point image de $z$ et $N$ est le point d'intersection du cercle trigonométrique $\mathcal{C}$ et la demi-droite $[OM)$. Donc, le point $N$ a pour coordonnées $(cos(\theta) ; sin(\theta))$. Ainsi, l'affixe du point $N$ est $z_N=cos(\theta)+isin(\theta)$. Or, $|z|=OM$ et $\overrightarrow{ON}=\dfrac{1}{OM}\overrightarrow{OM}=\dfrac{1}{|z|}\overrightarrow{OM}$, donc $\overrightarrow{OM}=|z|\overrightarrow{ON}$, ainsi $z=|z|(cos(\theta)+isin(\theta))$, d'où, $x+iy = |z|cos(\theta)+i|z|sin(\theta)$, ainsi, $x=|z|cos(\theta)$, soit $cos(\theta)=\dfrac{x}{|z|}$ et $y=|z|sin(\theta)$, soit $sin(\theta)=\dfrac{y}{|z|}$. | 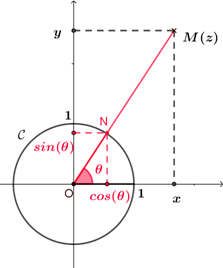 |
- Dans le plan complexe, placer les points A et B d'affixes respectives $3+3i$ et $-2+2i$.
- Déterminer un argument de l'affixe de A, puis de B.
- En déduire la mesure de l'angle $\widehat{AOB}$ et la nature du triangle AOB.
- A et B sont les points du plan complexes : $z_A=-2\sqrt{3}+2i$ et $z_B=\overline{z}_A$.
- Déterminer un argument de l'affixe de chacun des points A et B.
- En déduire la mesure de l'angle $\widehat{AOB}$.
- Démontrer que le triangle AOB est équilatéral.
-
Déterminer un argument du nombre complexe $z=-1+i\sqrt3$.
Soit $z_1$ un nombre complexe tel que |z|=3 et $arg(z_1)=\dfrac{3\pi}{2} ~[2\pi]$. Déterminer la forme algébrqiue du nombre complexe $z_1$.
-
Déterminer un argument du nombre complexe $z_2=1+i$.
Déterminer dans le repère orthonormé $(O ; \vec{u},\vec{v})$, l'ensemble des points $M$ d'affixe $z$ tels que $arg(z)= \dfrac{\pi}{4} ~[2\pi]$
Forme trigonométrique d'un nombre complexe
$z$ est un nombre complexe non nul.
L'écriture $z=|z|(cos(\theta)+isin(\theta))$ où $arg(z)=\theta ~[2\pi]$ est appelée une forme trigonométrique de $z$.
Deux nombres complexes non nuls sont égaux si, et seulement si, ils ont le même module et même argument à un multiple de $2\pi$ près.
Si $z=r(cos(\theta)+isin(\theta))$ avec $r$ un réel strictement positif alors $|z|=r$ et $arg(z)=\theta$ $~[2\pi]$
- Déterminer le module et un argument de chaque nombre complexe puis l'écrire sous forme trigonométrique.
$z_1=\dfrac{2}{5}i$, $z_2=1+i\sqrt{3}$, $z_3=-4i$, $z_4=-10$, $z_5=2-2i\sqrt{3}$ et $z_6=-1+i$.
- En déduire, sans calculs supplémentaires, une forme trigonométrique de $z_6$, $\overline{z_6}$ et $\sqrt{2}z_6$.
Dans chaque cas, écrire sous forme algébrique le nombre complexe $z$.
- $z=2\left(cos\left(\dfrac{\pi}{4}\right)+isin\left(\dfrac{\pi}{4}\right)\right)$
- $z=\sqrt{3}\left(cos\left(\dfrac{\pi}{3}\right)+isin\left(\dfrac{\pi}{3}\right)\right)$
- $z=\sqrt{3}\left(cos\left(-\dfrac{\pi}{6}\right)+isin\left(-\dfrac{\pi}{6}\right)\right)$
- $z=8\left(cos\left(\dfrac{3\pi}{4}\right)+isin\left(\dfrac{3\pi}{4}\right)\right)$
$z$ est un nombre complexe non nul de forme algébrique $z=x+iy$ avec $x\in \mathbb{R}$ et $y\in \mathbb{R}$ et dont une forme trigonométrique est $z=r(cos(\theta)+isin(\theta))$ avec $z=a+ib$ avec $r$ et $\theta$ des réels et $r>0$.
Voici une fonction FT qui :
-
prend en paramètres deux nombres réels
aetbqui correspondent respectivement aux parties réelle et imaginaire d'un nombre complexe $z$, -
renvoie le triplet
r,c,scorrespondant respectivement au module de $z$, à $cos(\theta)$ et à $sin(\theta)$.
from math import *
def FT(a,b):
r = ..................
c = ..................
s = .................
return r, c, s
- Compléter les lignes 3, 4 et 5 de ce programme
- Saisir et tester cette fonction
Pour tester cette fonction, vous pouvez utiliser Edupython ou directement le Trinket ci-dessous :
Exercices
Module et arguments d'un nombre complexes
On considère les nombres complexes : $a=1+i\sqrt{3}$ et $b=\sqrt{3}+i$.
On note $A$ et $B$ les points d'affixes $a$ et $b$.
-
- Donner une forme trigonométrique du nombre complexe $a$, puis de $b$.
- Placer précisment les points $A$ et $B$ dans le plan complexe.
- Démontrer que le triangle OAB est rectangle isocèle en O.
- $K$ est le milieu du segment $[AB]$.
- Placer le point $K$.
- Calculer son affixe.
-
On considère le nombre complexe $c=1-\sqrt{3}+i(1-\sqrt{3})$.
On note $C$ le point d'affixe $c$.
- Montrer que $K$ est le milieu de $[OC]$.
- Placer le point $C$ et montrer que le quadrilatère $OACB$ est un carré.
On se place dans le plan complexe d'origine O.
- Pour tout entier naturel $n$, on note $A_n$ le point d'affixe $z_n$.
- Démontrer que, pour tout entier naturel $n$, $\dfrac{z_{n+4}}{z_n}$ est réel.
- Démontrer alors que, pour tout entier naturel $n$, les points O, $A_n$ et $A_{n+4}$ sont alignés.
-
- Montrer que pour tout entier naturel $n$, $z_n = \dfrac{(1 + \text{i})^{n+1}}{2^n}.$
- En déduire pour quelles valeurs de $n$ les points $A_n$ appartiennent-ils à l'axe des abscisses ?
On donne les points $A$ et $B$ d'affixes $z_A=1+i\sqrt{3}$ et $z_B=2i$.
-
- Donner une forme trigonométrique de $z_A$ et $z_B$.
- Placer avec précision ces points sur une figure.
- $F$ est le point d'affixe $z_F=z_A+z_B$.
- Placer sur la figure le point $F$.
- Donner la forme algébrique de $z_F$.
- Démontrer que OAFB est un losange.
-
- Justifier que $\widehat{UOF}=\dfrac{5\pi}{12}$ et écrire une forme trigonométrique de $z_F$.
- Démontrer alors que : $cos\left(\dfrac{5\pi}{12}\right)=\dfrac{\sqrt{6}-\sqrt{2}}{4}$ et $sin\left(\dfrac{5\pi}{12}\right)=\dfrac{\sqrt{6}+\sqrt{2}}{4}$.
$A$ et $B$ sont les points d'affixes respectives : $z_A=1$ et $z_B=5$
$\Delta$ est la médiatrice du segment $[AB]$
A tout point $M$ d'affixe $z$, différent de A, on associe le point $M'$ d'affixe $z'$ telle que : $z'=\dfrac{2z-10}{z-1}$.
On se propose de déterminer l'ensemble $\mathscr{E}$ des points $M'$ lorsque $M$ parcourt $\Delta$.
- Conjecture avec un logiciel de géométrie
- Placer les points $A$ et $B$ en saisissant par exemple :
- Créer la médiatrice $\Delta$ du segment $[AB]$ et placer un point $M$ sur $\Delta$.
- Placer le point $M'$ en saisissant :

- Afficher la trace de $M'$ et déplacer le point $M$ afin de conjecturer la nature de l'ensemble $\mathscr{E}$.
- Démonstration
- Justifier que $|z-5|=|z-1|$ et en déduire que $|z'|=2$.
- Que peut-on dire alors du point $M'$ et de l'ensemble $\mathscr{E}$ ?
F est un point d'affixe $f$ avec $|f|=2$ et $f\neq 2$.
Démontrer qu'il existe un point $K$ d'affixe $k$, de la droite $\Delta$ tel que : $f=\dfrac{2k-10}{k-1}$.
- Déterminer alors l'ensemble $\mathscr{E}$.
$M$ d'affixe est un point quelconque de $\Delta$.
A tout nombre complexe $z$, différent de $-i$, on associe le nombre complexe $z'$ défini par : $z'=\dfrac{1+iz}{1-iz}$.
On note $M$ le point d'affixe $z$, et $M'$ le point d'affixe $z'$
On se propose de déterminer l'ensemble des nombres complexes $z'$ lorsque $z$ est un réel.
Donner la forme algébrique de $z'$ dans chacun des cas suivants :
- $z=3$
- $z=-4$
- $z=i$
- $z=1+i$
- Conjecture avec un logiciel de géométrie
Sur la figure ci-dessous, nous avons place un point $M$ d'affixe $z$, sur l'axe des abscisses.
Saisissez :
- Déplacer la point $M$ afin de conjecturer la nature de l'ensemble des nombres complexes $z'$.
-
- Démontrer que si $z$ est un nombre réel, alors $z'$ appartient à l'ensemble $\mathbb{U}$ des nombres complexes de module 1
- La réciproque de l'implication précédente est-elle vraie ? Le démontrer.
- $A$, $B$ et $C$ sont les points d'affixes $z_A=1$, $z_B=i$ et $z_C=3+2i$.
$M$ désigne un point du plan complexe d'affixe $z$.
- Ecrire en fonction de $z$ les normes des vecterus $\overrightarrow{AM}$, $\overrightarrow{BM}$ et $\overrightarrow{CM}$
- Déterminer l'ensemble $\mathscr{E}$ des points $M$ tel que : $|z-1|=|z-i|$ et $|z-3-2i|\leq 2$
Le plan complexe est muni d'un repère orthonormé direct $(O;\vec{u},\vec{v})$.
A tout point $M$ d'affixe $z$ non nulle, on associe le point $M'$ d'affixe $z'$ telle que : $z'=-\dfrac{1}{\overline{z}}$.
On se propose de déterminer l'ensemble $\mathscr{E}$ des points $M'$ lorsque $M$ parcourt $\Delta$.
-
- Montrer que $z'=-\dfrac{z}{|z|^2}$
- En déduire que les points $O, M, M'$ sont alignés.
- Démontrer que $\overline{z'+1}=\dfrac{1}{z}(z-1)$.
On nomme $A$ et $B$ les points d'affixes respectivement $1$ et $-1$.
On désigne par $\Gamma$ le cercle de centre $A$ contenant le point $O$. $\Gamma^*$ désigne le cercle $\Gamma$ privé du point $O$.
On suppose dans cette question que le point $M$ appartient à $\Gamma^*$.
Justifier l'égalité $|z-1|=1$.
Démontrer que $|z'+1|=|z'|$. Interpréter géométriquement cette égalité.
Déduire de ce qui précède une construction géométrique du point $M'$ à partir du point $M$.
On désigne par $\mathscr{C}$ le cercle de diamètre $[AB]$. On suppose dans cette question que le point $M$ appartient à $\mathscr{C}$.
Démontrer que $M'$ appartient à $\mathscr{C}$ et construire $M'$.
-
-
Calculer $z_{1}, z_{2}$ et $z_{3}$.
Placer les points $A_{1}$ et $A_{2}$ sur le graphique ci-dessous.
Écrire le nombre complexe $\dfrac{1 + \text{i}}{2}$ sous forme trigonométrique.
Démontrer que le triangle $OA_{0}A_{1}$ est isocèle rectangle en $A_{1}$.
-
-
-
Démontrer que la suite $\left(r_{n}\right)$ est géométrique, de raison $\dfrac{\sqrt{2}}{2}$.
-
La suite $\left(r_{n}\right)$ est-elle convergente ?
-
Interpréter géométriquement le résultat précédent.
-
-
-
Démontrer que pour tout entier naturel $n \::\: A_{n}A_{n+1} = r_{n+1}$.
-
Donner une expression de $L_{n}$ en fonction de $n$.
-
Déterminer la limite éventuelle de la suite $\left(L_{n}\right)$.
On note $L_{n}$ la longueur de la ligne brisée qui relie le point $A_{0}$ au point $A_{n}$ en passant successivement par les points $A_{1}, A_{2}, A_{3}$, etc.
Ainsi $L_{n} = \displaystyle\sum_{i=0}^{n-1} A_{i}A_{i+1} = A_{0}A_{1} + A_{1}A_{2} + \ldots + A_{n-1}A_{n}.$
-
Synthèses
$(0 ; \vec{u},\vec{v})$ est un repère orthonormé direct du plan complexes.
Pour la figure, on pendra pour unité 5 cm.
On considère la suite $(z_n)$ définie par $\left\{ \begin{array}{l} z_0=0\\ z_{n+1}=\dfrac{1}{2}(1+i) z_n-1+i \textrm{, pour tout } n\in\mathbb{N} \end{array} \right.$
Pour tout entier naturel $n$, on note $M_n$ le point du plan complexe qui a pour affixe $z_n$
-
Déterminer la forme algébrique de $z_1$ , $z_2$, $z_3$ et $z_4$.
-
Placer, dans le plan complexe, les points $M_0$, $M_1$ , $M_2$, $M_3$ et $M_4$.
Voici une fonction Suite_1 écrite dans le langage Python.
- Saisir cette fonction et l'exécuter pour $n=1$, $n=2$, $n=3$ et $n=4$. Quels rsultats retrouve-t-on ainsi ?
- Utiliser cette fonction pour obtenir $z_5$ , $z_6$, $z_7$ et $z_8$.
-
Placer, dans le plan complexe, les points $M_5$, $M_6$ , $M_7$ et $M_8$.
- $(Z_n)$ est la suite définie sur $\mathbb{N}$ par $Z_n=z_n+2$.
- Quel est le vecteur dont l'affixe est $Z_n$ ?
- Montrer que pour tout $n\in\mathbb{N}$, $Z_{n+1}=\dfrac{1}{2}(1+i)Z_n$.
- Déterminer $Z_0$.
- Ecrire en langage Python, une fonction Suite_2 qui, pour une valeur $n$ du paramètre renvoie le nombre complexe $Z_n$.
- Saisir ce programme à l'aide de cette fonction, conjecturer une propriété des nombres $Z_{4k}$ et $Z_{4k+2}$, pour $k$ nombre entier naturel.
-
- Démontrer que pour tout entier naturel $n$, $Z_n=\dfrac{(1+i)^n}{2^{n-1}}$. En déduire l'exprerssion de $z_n$ en fonction de $n$.
- Démontrer que pour tout entier naturel $k$, $(1+i)^{4k}$ est un nombre réel et $(1+i)^{4k+2}$ est un imaginaire pur. Que peut-on en déduire pour les points $M_{4k}$ et $M_{4k+2}$ ?
from cmath import *
def Suite_1(n):
z=0
for i in range(1,n+1):
z=(1+1j)/2*z-1+1j
return z cmath pour travailler avec les nombres complexes.
Les complexes se notent : 1+1j, 3j, -1+0j, ...
Ecrire l'expression de $Z_{n+1}$ et mettre $1+i$ en facteur.
Exécuter ce programme pour des paramètres de la forme $4k$ et $4k+2$.
- Démontrer que pour tout entier naturel $n$, $|Z_n|=2\times\left(\dfrac{\sqrt{2}}{2}\right)^n$
- Quelle est la limite de la suite $(|Z_n|)$ lorsque $n$ tend vers $+\infty$.
- Interpréter géométriquement ce résultat.
Le plan complexe est muni d'un repère orthonormé direct.
Résultats préliminaires
$Z$ désigne u nombre complexe.
- Démontrer que $Re(Z)\leqslant |Z|$.
- Démontrer que $Re(Z)=|Z|$ si, seulement si, $Z$ est un nombre réel positif.
- Inégalité triangulaire pour deux nombres complexes
$z$ et $z'$ désignes deux nombres complexes.
À partir de l'égalité $|z+z'|^2=(z+z')(\overline{z+z'})$, démontrer que :
$|z+z'|^2=|z|^2+2Re\left(z+\overline{z'}\right)+|z'|^2$À l'aide de l'inégalité de la question 1.a., démontrer que : $|z+z'|^2\leqslant|z|^2+2|z|z'|+|z'|^2$
En déduire alors l'inégalité triangulaire : $|z+z'|\leqslant|z|+|z'|$.
À l'aide de 1.b., démontrer que $|z+z'|\leqslant|z|+|z'|$ si, seulement si, $z\overline{z'}$ est un nombre réel positif.
Etude géométrique du cas d'égalité
On donne la forme algébrique des nombres complexes $z$ et $z'$ :
$z=x+iy$ et $z'=x'+iy'$ avec $x$, $y$, $x'$, $y'$ nombres réels.
Exprimer $z\overline{z'}$ en fonction de $x$, $y$, $x'$ et $y'$.
Montrer que $z\overline{z'}$ est un nombre réel positif si, et seulement si,
\[\text{ (1) }\left\{\begin{array}{l c l} xy'-x'y&=&0\\ xx'+yy'&\geqslant&0\\ \end{array}\right.\]Dans le plan complexe, on note $\vec{u}$ et $\vec{v}$ les vecteurs d'affixes respectives $z$ et $z'$.
Traduire le système (1) à l'aide du déterminant du couple $(\vec{u} ; \vec{v})$ et du produit scalaire $\vec{u}.\vec{v}$.
- En déduire que $z\overline{z'}$ est un nombre réel positif si, seulement si, les vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires et de même sens.
- Une conséquence de l'inégalité triangulaire $z$ et $z'$ désignent deux nombres complexes.
Démontrer que $|z|\leqslant|z-z'|+|z'|$ et en déduire que $|z|-|z'|\leqslant|z-z'|$
Démontrer que : $|z'|-|z|\leqslant|z-z'|$
En déduire un encadrement de $|z|-|z'|$
- Justifier alors l'inégalité $\lvert|z|-|z'|\rvert\leqslant|z-z'|$ .
Savoirs et savoirs-faire
-
la notion d'image et d'affixe,
-
la notion du module d'un nombre complexe,
-
la notion d'argument d'un nombre complexe non nul,
-
interpréter géométriquement le module d'un nombre complexe,
-
interpréter géométriquement un argument d'un nombre complexe non nul,
-
refaire la démonstration de la formule $z^2=z\overline{z}$,
-
refaire la démonstration du module d'un produit,
-
refaire la démonstration du module d'une puissance,
-
déterminer et utiliser des affixes,
-
calculer et utiliser le module d'un nombre complexe,
-
déterminer et utiliser un argument d'un nombre complexe non nul,

Maths expertes de Auteurs : Thomas Lourdet, Johan Monteillet, est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.