Rappels sur le cercle trigonométrique

Voici un rappel (ou un complément) du programme de spécialité mathématiques de première sur les fonctions trigonométriques et le cercle trigonométrique.

Définitions

On peut "enrouler" l'axe des réels autour d'un cercle de rayon 1, comme l'illustre l'animation ci-dessous :

On appelle cercle trigonométrique $\mathcal{C}$ dans le plan muni du repère orthonormal $(O ; \overrightarrow{i}, \overrightarrow{j})$ le cercle de centre $O$, de rayon $1$, pour lequel on choisit pour sens direct le sens inverse des aiguilles d’une montre.
À tout nombre réel $x$, on associe le point unique $M$ du cercle $\mathcal{C}$ tel qu’une mesure, en radians, de l’angle orienté $(\overrightarrow{i},\overrightarrow{OM})$ soit $x$.
Soit $x$ un réel et soit $M$ le point de $\mathcal{C}$ tel que $(\overrightarrow{i},\overrightarrow{OM})=x$.
Le point $M$ a pour abscisse $\cos(x)$ et pour ordonnées $\sin(x)$.

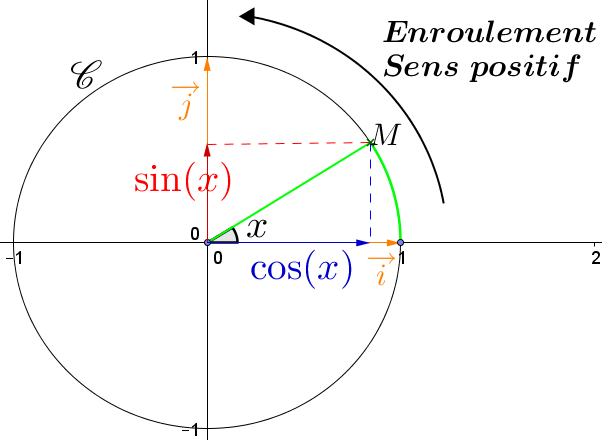
Comme un tour complet du cercle trigonométrique correspond à un angle de $2\pi$ (radians), si une mesure de $(\overrightarrow{i},\overrightarrow{OM})$ est $x$ alors les autres mesures sont : $x+k 2\pi$ avec $k\in\mathbb{Z}$.

Pour tout réel $x$ :

$-1\le \cos(x) \le 1$.
$-1\le \sin(x) \le 1$.
$(\cos(x))^2+(\sin(x))^2 = 1$.

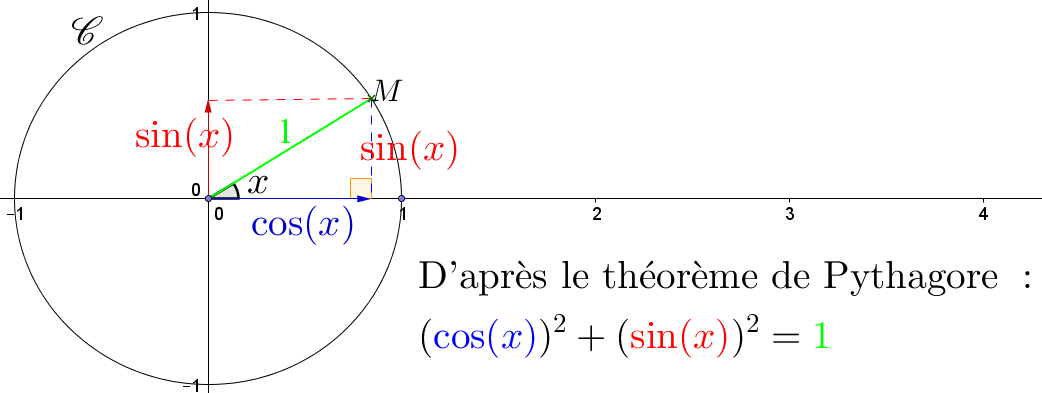
Valeurs à connaître par cœur

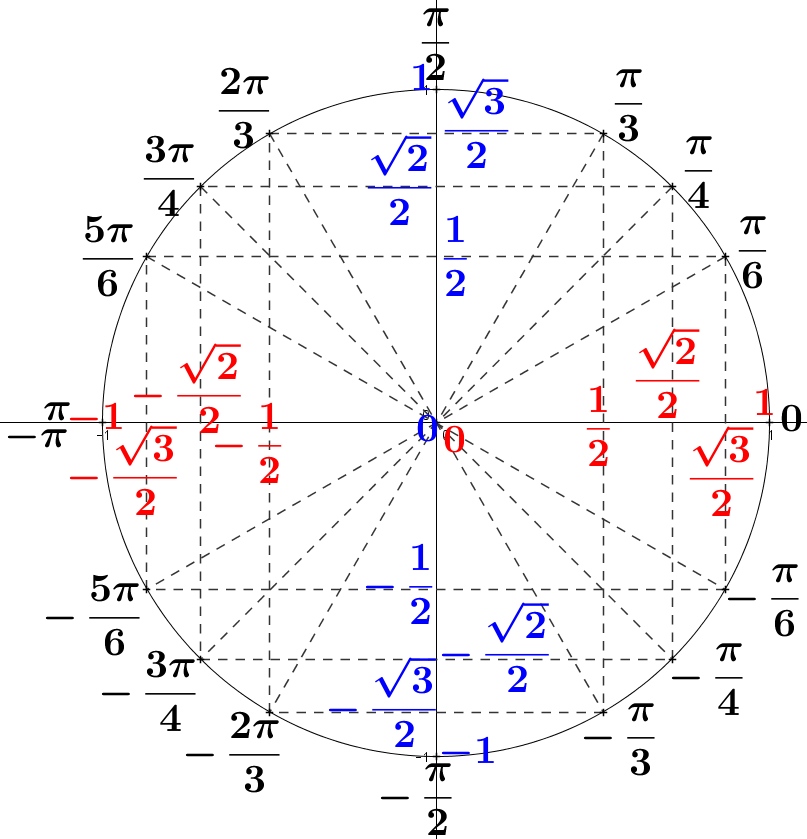
En utilisant la relation $(\cos(x))^2+(\sin(x))^2 = 1$, on peut démontrer les valeurs suivantes :

$x$	$0$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$
$\sin(x)$	$0$	$\dfrac{1}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{\sqrt{3}}{2}$	$1$
$\cos(x)$	$1$	$\dfrac{\sqrt{3}}{2}$	$\dfrac{\sqrt{2}}{2}$	$\dfrac{1}{2}$	$0$

À partir de ces valeurs, on peut déduire l'ensemble des valeurs remarquables à connaître au lycée sur le cercle trigonométrique :

Cercle complet à connaître par cœur :

Voici un test de six questions à faire en autonomie afin de vérifier votre maîtrise des valeurs angulaires à connaître sur le cercle trigonométrique.

Voici un test de dix questions à faire en autonomie afin de vérifier votre maîtrise des valeurs remarquables trigonométriques à connaître sur le cercle trigonométrique.

Exercices

De mémoire, construire le cercle trigonométrique complet précis sur l'intervalle $[-\pi;\pi]$ où apparaissent à la fois les angles remarquables $x$ et les valeurs correspondantes $\cos(x)$ et $\sin(x)$.

Utiliser le cercle trigonométrique afin de résoudre les équations suivantes sur $[-\pi ;\pi]$ :

$\sin(x)=\dfrac{1}{2}$

Code de déblocage de la correction :
$\cos(x)=-\dfrac{\sqrt{3}}{2}$

Code de déblocage de la correction :
$2(\sin(x))^2=1$

Code de déblocage de la correction :
$2(\sin(x))^2-\sqrt{3} \sin(x)-3=0$

Poser $X=\sin(x)$ afin de se ramener à une équation du second degré.
Après avoir résolu cette équation en $X$, penser à en déduire les valeurs possibles de l'inconnue $x$.

Code de déblocage de la correction :
$\cos(x)=\dfrac{\sqrt{2}}{2}$

Code de déblocage de la correction :
$(2\sin(x)+1)(\sqrt{3}-2\cos(x))=0$

Code de déblocage de la correction :
$4(\cos(x))^2-1=0$

Code de déblocage de la correction :
$4(\cos(x))^2-\sqrt{6}=2(\sqrt{3}-\sqrt{2}) \cos(x)$

Démontrer que $\sqrt{20+8\sqrt{6}}=2\sqrt{3}+2\sqrt{2}$.

Code de déblocage de la correction :
$(\cos(x)+1)\cos(x)\sin(x)=0$

Code de déblocage de la correction :

Une scène de concert comporte un arc permettant de placer des projecteurs à différents points de cet arc.

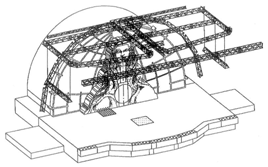
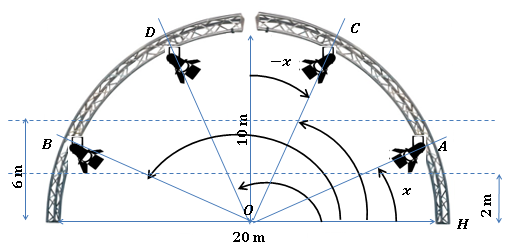
Le projecteur A se trouve à la position formant un angle de $\dfrac{\pi}{6}$ par rapport à l’horizontale.
À quelle hauteur se situent les projecteurs A et C dans la scène ?

Voici un test de quatre questions à faire en autonomie afin de vérifier votre maîtrise de la résolution d'équations trigonométriques en s'aidant du cercle trigonométrique.

Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲