Demander le programme !

Un résumé de cours en version imprimable est téléchargeable ici.
Résolution d'équations du second degré à coefficients réels
Équations du type $z^2=a$
-
Quelles sont les solutions réelles de l'équation $x^2=4$ ?
-
Quels nombres complexes $z$ connaissez-vous qui sont solution de l'équation $z^2=-1$ ?
-
-
Quelles sont les solutions réelles de l'équation $x^2=-4$ ?
-
Pouvez-vous trouver des solutions complexes $z$ de l'équation $z^2=-4$ ?
-
Soit $a$ un nombre réel.
Si $a$ est non nul, l'équation $z^2=a$ admet toujours deux solutions complexes.
Plus précisément :
-
Si $a=0$, l'équation $z^2=a$ admet une unique solution complexe : 0.
-
Si $a>0$, l'équation $z^2=a$ admet deux solutions réelles : $\sqrt{a}$ et $-\sqrt{a}$.
-
Si $a<0$, l'équation $z^2=a$ admet deux solutions complexes conjuguées : $i\sqrt{|a|}$ et $-i\sqrt{|a|}$.
-
Cas ou $a=0$ :
Démontrer que 0 est l'unique solution de l'équation $z^2=0$. -
Cas ou $a>0$ :
-
Factoriser $z^2-a$ à l'aide de $\sqrt{a}$ et de $-\sqrt{a}$.
-
En déduire que si $a>0$, alors l'équation $z^2=a$ admet deux solutions réelles : $\sqrt{a}$ et $-\sqrt{a}$.
-
-
Cas ou $a<0$ :
-
Développer $\left(z-i\sqrt{|a|}\right)\times\left(z+i\sqrt{|a|}\right)$.
-
En déduire que si $a<0$, alors l'équation $z^2=a$ admet deux solutions complexes conjuguées : $i\sqrt{|a|}$ et $-i\sqrt{|a|}$.
-
Résoudre dans $\mathbb{C}$ les équations suivantes :
-
$z^2+100=0$.
-
$z^2-8=0$.
-
$z^4=81$.
-
$(2z+1)^2=25$.
-
$z^2+2iz-1=0$.
penser à factoriser.
Équations du type $az^2+bz+c=0$
Vous avez découvert en première comment résoudre des équations du second degré dans $\mathbb{R}$ en utilisant le second degré.
Le théorème suivant prolonge et précise ce que vous connaissez déjà :
On considère l'équation du second degré $az^2+bz+c=0$, d'inconnue $z$, où $a$, $b$ et $c$ sont des réels avec $a\neq 0$.
Le discriminant de cette équation du second degré est $\Delta=b^2-4ac$.
-
Si $\Delta>0$, l'équation admet deux solutions réelles distinctes :$z_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b+\sqrt{\Delta}}{2a}$.
-
Si $\Delta=0$, l'équation admet une solution réelle, dite racine double, $z_0=\dfrac{-b}{2a}$.
-
Si $\Delta<0$, l'équation admet deux solutions complexes conjuguées distinctes : $z_1=\dfrac{-b-i\sqrt{|\Delta|}}{2a}$ et $z_2=\dfrac{-b+i\sqrt{|\Delta|}}{2a}$.
-
Démontrer que, pour tout nombre complexe $z$, on a : $a\left(\left(z+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right)=az^2+bz+c$.
-
En déduire que si $\Delta=0$ alors l'équation $az^2+bz+c=0$ admet une unique solution : $z=-\dfrac{b}{2a}$.
-
-
Résoudre dans $\mathbb{C}$ l'équation $a\left(\left(z+\frac{b}{2a}\right)^2-\frac{\Delta}{4a^2}\right)=0$.
-
En déduire que si $\Delta>0$, l'équation $az^2+bz+c=0$ admet deux solutions réelles distinctes : $z_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b+\sqrt{\Delta}}{2a}$.
Cas où $\Delta>0$ :
-
-
-
Simplifier $\left(i\sqrt{|\Delta|}\right)^2$.
-
En déduire que si $\Delta<0$, l'équation $az^2+bz+c=0$ admet deux solutions complexes conjuguées distinctes : $z_1=\dfrac{-b-i\sqrt{|\Delta|}}{2a}$ et $z_2=\dfrac{-b+i\sqrt{|\Delta|}}{2a}$
Cas où $\Delta<0$ :
-
-
Résoudre dans $\mathbb{C}$ l'équation : $z^2-4z=-5$.
-
Résoudre dans $\mathbb{C}$ l'équation : $z^2+3z+4=0$.
Résoudre dans $\mathbb{C}$ l'équation : $z^4+2z^2-8=0$.
Factorisation d'un polynôme du second degré
On considère le plynôme du second degré $P$ tel que, pour tout nombre complexe $z$, on ait $P(z)=az^2+bz+c$, où $a$, $b$ et $c$ sont des réels avec $a\neq 0$.
On note $z_1$ et $z_2$ les solutions dans $\mathbb{C}$ de l'équation $az^2+bz+c=0$, avec éventuellement $z_1=z_2$.
Alors on obtient la factorisation suivante : pour tout nombre complexe $z$ , $az^2+bz+c=a(z-z_1)(z-z_2)$
Dans le cas d'une racine double où $z_1=z_2=z_0=-\dfrac{b}{2a}$, cette factorisation s'écrit : $az^2+bz+c=a(z-z_0)^2$.
Factoriser dans $\mathbb{C}$ le polynôme $P$ défini par $P(z)=4z^2-12z+10$.
Équation polynomiale à coefficients réels
Définitions
Soit $n\in\mathbb{N}$.
On appelle polynôme $P$ de degré $n$ à coefficients réels toute expression pouvant s'écrire sours la forme $P(z)=a_n\times z^n+a_{n-1}\times z^{n-1}+...+a_2\times z^2+a_1 z+a_0$, avec $a_n$, $a_{n-1}$, ..., $a_2$, $a_1$ et $a_0$ des nombres réels où $a_n\neq 0$.
Un nombre complexe $a$ est appelé racine de $P$ si, et seulement si, $P(a)=0$.
$P(z)=z^3+2z^2+3z+4$ et $Q(z)=z(z^5-1)$ définissent des polynômes de degré respectivement 3 et 6 à coefficients réels.
Lorsque le polynôme comporte un unique terme, on parle de monôme.
$R(z)=6z^4$ est un monôme de degré 4.
Soit $a$ un nombre complexe quelconque.
On dit qu'un polynôme $P$ est factorisable (ou divisible) par $z-a$ si, et seulement si, il existe un polynôme $Q(z)$
tel que pour tout nombre complexe $z$, on a : $P(z)=(z-a)\times Q(z)$
Comme $z^4-4z^2-z+2=(z-2)\times(z^3+2z^2-1)$, $z^4-4z^2-z+2$ est factorisable par $z-2$.
Factorisation
Soit $a$ un nombre complexe quelconque.
Pour tout nombre complexe $z$ et pour tout entier naturel non nul $n$, $z^n-a^n$ est factorisable par $z-a$.
Plus précisément :
Démontrer l'égalité de la propriété ci-dessus.
Cette égalité peut être vue comme une généralisation du résultat vu en première sur les suites géométriques de raison $q\neq 1$ :
$$1+q^1+q^2+...+q^n=\dfrac{q^{n+1}-1}{q-1}$$Factoriser le polynôme $P(z)=z^3-27$.
Factoriser le polynôme $P(z)=z^7+i$.
Le polynôme $P$ est factorisable par $z-a$ si, et seulement si, $a$ est une racine de $P$.
-
Supposons que $P$ est factorisable par $z-a$.
Montrer $a$ est alors une racine de $P$. -
Supposons que $a$ soit une racine de $P$.
-
En notant $n$, avec $n\ge 1$, le degré de $P$, donner la forme développée de $P(z)$.
-
En déduire une expression de $P(a)$ puis de la différence $P(z)-P(a)$.
-
En regroupant les termes de même degré en $z$ et en $a$ et en utilisant la propriété de factorisation de $z^n-a^n$, démontrer que $P(z)-P(a)$ est factorisable par $z-a$.
-
-
Quel raisonnement permet de conclure ?
Un polynôme non nul de degré $n$ admet au plus $n$ racines ; autrement dit, le nombre de solutions d'une équation polynomiale est inférieur ou égal à son degré.
Un polynôme de degré $n$ s'annulant au moins en $n+1$ racines distinctes est forcément le polynôme nul.
Voici ci-dessous une démonstration incomplète et en partie erronée du théorème précédent.
Lire cette démonstration puis répondre aux questions suivantes afin de l'améliorer.
Soient $n$ un entier naturel non nul et la propriété $(P_n)$ : "tout polynôme de degré $n$ a au plus $n$ racines".
Montrons que la propriété $(P_n)$ est vraie pour tout entier naturel non nul.
Initialisation : pour $n=1$
Tout polynôme de degré 1 est de la forme $P(z)=az+b$ avec $a\neq 0$.
Affirmation 1 : il admet donc une unique racine ; la propriété $(P_1)$ est donc vraie .
Hérédité :
On suppose que la propriété $(P_k)$ est vraie pour tout entier $k\ge 1$, c'est-à-dire que "tout polynôme de degré $k$
a au plus $k$ racines".
Montrons la propriété $(P_{k+1})$ est vraie, c'est-à-dire que "tout polynôme de degré $k+1$ a au plus $k+1$ racines".
Soit $Q$ un polynôme de degré $k+1$.
Raisonnement 1 : on a deux possibilités :
-
soit $Q$ n'a pas de racine.
Affirmation 2 : dès lors l'affirmation "Q a au plus $k+1$ racines" est vraie . -
soit $Q$ admet au moins une racine, notée ici $a$.
$Q$ peut donc être factorisé par le polynôme $z-a$.
Il existe donc un polynôme $R$ Affirmation 3 : de degré $k$ tel que $Q(z)=(z-a)\times R(z)$Ainsi : $Q(z)=0 \iff (z-a)\times R(z) =0 \iff z-a=0 \text{ ou } R(z)=0$
Affirmation 4 : $R$ a au plus $k$ racines, dès lors Affirmation 5 : l'équation $Q(z)=0$ admet donc au plus $k+1$ solutions.
dès lors l'affirmation "Q a au plus $k+1$ racines" est vraie .
Affirmation 6 : Ainsi, la propriété est héréditaire.
Comme la propriété est initialisée avec $n=1$ et est héréditaire, elle est vraie pour tout entier naturel $n\ge 1$.
-
Quel est le raisonnement principal mis en oeuvre dans cette démonstration ?
-
Justifier l'affirmation 1.
-
Corriger la rédaction de la structure de la phase d'hérédité.
-
Comment s'appelle le type de raisonnement du Raisonnement 1 ?
-
Justifier l'affirmation 2.
-
Justifier le degré $k$ du polynôme $R$ énoncé dans l'affirmation 3.
-
Justifier l'affirmation 4.
-
Justifier l'affirmation 5.
-
Justifier l'affirmation 6.
Exercices
Second degré
Résoudre dans $\mathbb{C}$ les équations suivantes :
-
$z^2+64=0$
-
$z^2-12=0$
-
$(z^2+9)(4z^2+1)=0$
-
$z^2+64z=0$
-
$3z^2+1=28$
-
$z^2(3i-z)=0$
Résoudre dans $\mathbb{C}$ les équations suivantes et donner les résultats sous forme algébrique.
- $z^2+4=0$
- $iz^2+(3-4i)z=0$
- $z^2-2z+4=0$
- $z^2-8z+25=0$
- $z^2+2\sqrt{3}z+3=0$
- $z^2-(2+3i)^2=0$
-
Prouver que $2+i$ est solution de l'équation $z^2+5=4z$.
-
En déduire sans calcul l'ensemble des solutions de l'équation $z^2+5=4z$.
Résoudre dans $\mathbb{C}$ les équations suivantes et donner les résultats sous forme algébrique.
- $(2iz+i)(4z-8-4i)=0$
- $(z^2+2)(z^2-4z+4)=0$
- $\dfrac{z-3}{z-2}=z$
- $z^2-2(1+\sqrt{2})z+2(\sqrt{2}+2)=0$
Résoudre les systèmes suivant :
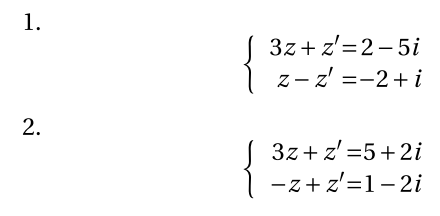
Écrire chacune des expressions suivantes sous la forme $z^n-a^n$, où $a$ est un nombre complexe et $n$ un entier naturel afin d'en déduire une factorisation de ces expressions.
-
$z^3-8$
-
$z^3+27$
-
$z^3-27i$
-
$z^5-32i$
On considère l'équation $(E) : z^4-z^2-1=0$.
-
Résoudre dans $\mathbb{C}$ l'équation $(E') : Z^2-Z-1=0$.
-
En déduire la résolution dans $\mathbb{C}$ de l'équation $(E) : z^4-z^2-1=0$.
Équations polynomiales
On considère la fonction polynomiale $P$ définie pour tout nombre complexe $z$ par $P(z)=z^3-12z^2+37z-40$.
On admet qu'il existe un réel $k$ tel que : $P(z)=(z-k)(z^2-4z+5)$.
En déduire une racine réelle de $P$.
On donne l'équation $(E)$ : $$z^3-12z^2+48z-128=0.$$
- Vérifiez que 8 est solution de $(E)$.
-
- Déterminez des réels $a$, $b$ et $c$ tels que pour tout $z$ de $\mathbb{C}$, $$z^3-12z^2+48z-128=(z-8)(az^2+bz+c)$$
- Résolvez dans $\mathbb{C}$ l'équation $(E)$.
On appelle dans cet exercice "solution évidente" une solution d'une équation polynomiale appartenant à l'ensemble suivant : ${-3;-2;-1;0;1;2;3}$.
-
Écrire en langage Python une fonction
admet_sol_evidentequi :-
prend comme paramètre une fonction polynômiale $P$,
-
renvoie le booléen
Truesi l'équation $P(z)=0$ admet une "solution évidente" et le booléenFalsesinon.
Par exemple :
Si on considère l'équation $4z^3+3z^2+2z-1=0$, on définit d'abord la fonction $P$ qui prend comme argument $z$ et renvoie $4z^3+3z^2+2z-24$.
Ensuite,
admet_sol_evidente(P)renvoieTruecar $P(-2)=0$. -
-
-
Déterminer si la fonction polynomiale $P$ définie par $P(z)=z^3-4z^2+z+6$ admet ou non une "solution évidente".
-
En déduire l'ensemble des solutions complexes de l'équation polynomiale $z^3-4z^2+z+6=0$.
-
-
Résoudre dans $\mathbb{C}$ l'équation polynomiale $2z^4-39z^3+56z^2+51z-36=0$.
On considère l'équation suivante : $z^3-3z^2+25z+29=0$.
-
Vérifier que -1 est une solution de cette équation.
-
En déduire une factorisation de $z^3-3z^2+25z+29$.
-
En déduire l'ensemble des solutions complexes de l'équation $z^3-3z^2+25z+29=0$.
Justifier les réponses de ce VRAI ou FAUX.
On se place dans un repère orthonormé direct $(O ; \overrightarrow{u}, \overrightarrow{v})$.
-
Soit (E) l'équation d'inconnue $z$ : $z^2+7=0$.
On note $A$ et $B$ les points dont les affixes sont les solutions de cette équation.
Affirmation 1 :La droite $(AB)$ passe par l'origine $O$.
-
Soit (E) l'équation d'inconnue $z$ : $z^2-2\sqrt{3}z+4=0$.
On note $A$ et $B$ les points dont les affixes sont les solutions de cette équation.
Affirmation 2 :Le triangle $OAB$ est équilatéral.
On munit le plan complexe d'un repère orthonormé direct $(O ; \overrightarrow{u}, \overrightarrow{v})$.
On considère l'équation (E) : $z^4+2z^3-z-2=0$.
-
Donner une solution entière de (E).
-
Vérifier que, pour tout nomnre complexe $z$, $z^4+2z^3-z-2=(z^2+z-2)(z^2+z+1)$.
-
Résoudre l'équation (E) dans $\mathbb{C}$.
-
Les solutions de l'équation (E) sont les affixes de quatre points du plan complexe nommés $A$, $B$, $C$ et $D$ tels que $ABCD$ est un quadrilatère non croisé.
Quelle est la nature de ce quadrilatère ?
On considère la fonction polynomiale $P$ définie par $P(z)=z^4-4z^3+17z^2-16z+52$.
-
Démontrer que si $z_0$ est une solution complexe de l'équation $P(z)=0$ alors $\overline{z_0}$ en est aussi une.
-
Déterminer un réel $y$ tel que $P(yi)=0$.
-
Justifier que $P(z)$ est factorisable par $z^2+4$.
-
Déterminer trois réels $a$, $b$ et $c$ tels que $P(z)=(z^2+4)(az^2+bz+c)$.
-
En déduire les solutions dans $\mathbb{C}$ de l'équation $P(z)=0$.
Exercices de synthèse
Partie A
Soit l'équation (E) : $z^4=-4$, où $z$ est un nombre complexe.
-
Montrer que si le nombre complexe $z$ est solution de l'équation (E) alors les nombres complexes $-z$ et $\overline{z}$ sont aussi solutions de l'équation (E).
-
Écrire le nombre complexe $z_0=1+i$ sous forme exponentielle.
-
En déduire que $z_0$ est une solution de (E).
-
Déduire, sans nouveau calcul, des questions précédentes l'ensemble des solutions de l'équation (E).
Partie B
On considère les points $A$, $B$, $C$ et $D$ du plan complexe d'affixes respectivers : $z_A=1+i$, $z_B=-1+i$, $z_C=-1-i$ et $z_D=1-i$.
-
Déterminer les affixes des points $E$ et $F$ définis par $z_E-z_C=(z_B-z_C)\times e^{-i\frac{\pi}{3}}$ et $z_F-z_C=(z_D-z_C)\times e^{-i\frac{\pi}{3}}$.
-
Démontrer que le quotient $\dfrac{z_A-z_E}{z_A-z_F}$ est un nombre réel.
-
Que peut-on dire des points $A$, $E$ et $F$ ? Justifier.
On considère le polynôme $P$ défini sur $\mathbb{C}$ par $P(z)=z^6-1$.
-
Factoriser l'expression $A^3-B^3$ pour tout nombre complexe $A$ et $B$.
-
En remarquant que $\displaystyle{z^6={(z^2)}^3}$, déterminer trois réels $a$, $b$ et $c$ tels que, pour tout nombre complexe $z$ de $\mathbb{C}$, on a : $P(z)=(z^2-1)(az^4+bz^2+c)$.
-
Calculer $\left(\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2}\right)^2$ et $\left(\dfrac{1}{2}-i\dfrac{\sqrt{3}}{2}\right)^2$.
-
En déduire les six racines de l'unité, c'est-à-dire les six racines dans $\mathbb{C}$ du polynôme $P$.
-
Mettre sous forme exponentielle chacune des solutions trouvées. Que remarquez-vous ?
Le but est de trouver une méthode pour tracer à la règle et au compas un pentagone régulier.
Partie A : Calcul de $\cos\left(\dfrac{2\pi}{5}\right)$
-
Factoriser $z^5-1$.
-
On pose $\omega=e^{i\frac{2\pi}{5}}$.
Justifier que $\omega$ est solution de $z^5-1=0$.
-
En déduire $1+\omega+\omega^2+\omega^3+\omega^4=0$.
-
Justifier que 1, $\omega$, $\omega^2$, $\omega^3$ et $\omega^4$ sont les racines de l'équation $z^5-1=0$.
-
-
Justifier que $u+v=-1$.
-
Montrer que $u\times v=-1$.
-
En déduire que $u$ et $v$ sont solutions de l'équation $x^2+x-1=0$.
-
En déduire les valeurs exactes de $u$ et de $v$.
-
En déduire que $\cos\left(\dfrac{2\pi}{5}\right)=\dfrac{-1+\sqrt{5}}{4}$.
On pose $u=\omega+\omega^4$ et $v=\omega^2+\omega^3$.
-
Partie B : Tracé précis d'un pentagone régulier
On munit le plan complexe d'un repère orthonormé direct $(O ; \overrightarrow{u}, \overrightarrow{v})$.
On appelle $\Omega_0$ le point d'affixe 1, $J$ celui d'affixe $i$ et $M$ celui d'affixe $-\dfrac{1}{2}$.
Vous pouvez utiliser le fichier Geogebra ci-dessous afin de réaliser progressivement les tracés demandés.
Déplacer les curseurs pour obtenir les coordonnées approchées de votre ville.
-
Soit $\mathcal{C}$ le cercle de centre $M$ passant par $J$.
Calculer l'affixe du point d'intersection $N$ du cercle $\mathcal{C}$ avec la demi-droite $[O\Omega_0)$.
-
Construire à la règle et au compas (ou en utilisant seulement des droites et des cercles sur Geogebra) le point $\Omega_1$ d'affixe $\omega$.
-
Construite à la règle et au compas les points $\Omega_2$, $\Omega_3$ et $\Omega_4$ d'affixe respective $\omega^2$, $\omega^3$ et $\omega^4$.
-
Finir par le tracé du pentagone régulier $\Omega_0 \Omega_1 \Omega_2 \Omega_3 \Omega_4$.
Le but de cet exercice est de découvrir une méthode pour résoudre par radicaux une équation de degré 3
Partie A : méthode de Cardan-Tartaglia
On considère l'équation (E) $x^3+px=q$ où $p$ et $q$ sont deux nombres réels.
On cherche à trouver une solution réelle $x$ de cette équation en écrivant $x$ sous la forme $u+v$, où $u$ et $v$ sont des réels.
-
Justifier que si $x=u+v$ alors $x^3=u^3+v^3+3u\times v\times x$.
-
En déduire que si on obtient des réels $u$ et $v$ tels que $\left \{ \begin{array}{rcl} u^3+v^3&=&q \\ u\times v&=&-\dfrac{p}{3} \end{array} \right.$ alors $x=u+v$ est solution de l'équation (E).
-
Poser $U=u^3$ et $V=v^3$.
Montrer que résoudre le système $\left \{ \begin{array}{rcl} u^3+v^3&=&q \\ u\times v&=&-\dfrac{p}{3} \end{array} \right.$ revient à résoudre le système $\left \{ \begin{array}{rcl} U+V&=&q \\ U\times V&=&-\dfrac{p^3}{27} \end{array} \right.$.
-
En déduire que résoudre le système $\left \{ \begin{array}{rcl} u^3+v^3&=&q \\ u\times v&=&-\dfrac{p}{3} \end{array} \right.$ revient à résoudre le système $\left \{ \begin{array}{rcl} U^2-qU-\dfrac{p^3}{27}&=&0 \\ V&=&q-U \end{array} \right.$.
-
En déduire qu'en posant $\Delta=\dfrac{27q^2+4p^3}{27}$, si $\Delta>0$ alors l'équation (E) admet au moins une solution réelle :
$$x=\sqrt[3]{\dfrac{-q+\sqrt{\Delta}}{2}}+\sqrt[3]{\dfrac{-q-\sqrt{\Delta}}{2}}$$ -
Utiliser cette méthode pour résoudre l'équation suivante : $x^3+24x=56$.
Partie B : Résolution générale d'une équation de degré 3
On considère dans cette partie une équation de degré 3 (E') de la forme $ax^3+bx^2+cx+d=0$, où les coefficients $a$, $b$, $c$ et $d$ sont des nombres réels tels que $a\neq 0$.
-
On pose $X=x-\dfrac{b}{3a}$.
Montrer que résoudre l'équation (E') $ax^3+bx^2+cx+d=0$ revient à résoudre l'équation (E'') $X^3+pX=q$, où $p$ et $q$ sont des nombres réels à exprimer en fonction des réels $a$, $b$, $c$ et $d$.
-
En utilisant les résultats précédents, résoudre l'équation suivante : $x^3-2x^2+x-2=0$.
Partie C : Équation de Bombelli
On considère dans cette partie l'équation $x^3-15x-4=0$.
-
Peut-on appliquer la méthode de Cardan-Tartaglia à cette équation ? Pourquoi ?
-
Justifier que l'équation $U^2-4U+125=0$ admet pour solutions complexes les nombres $2+11i$ et $2-11i$.
-
Calculer $(2+i)^3$ et $(2-i)^3$.
-
En déduire comment obtenir une solution réelle à l'équation $x^3-15x-4=0$.
La résolution générale de cette équation $x^3+px=q$ aurait été trouvée vers 1515 par le mathématicien Scipione del Ferro. Cependant, il garda jusqu'à sa mort sa découverte car à l'époque la chaire de professeur de mathématiques de l'Université de Bologne (en Italie) était remise en jeu à travers un concours de résolution de problèmes arithmtiques. Posséder cette résolution lui aurait permis de conserver jusqu'à sa mort cette chaire.
Niccolò Fontana dit Tartaglia
(son surnom signifie le bègue) est un mathématicien autodidacte italien ayant vécu environ de 1500 à 1557.
Issu d'un milieu modeste, il gagne sa vie en enseignant les mathématiques et en participant à des concours. Ce serait en 1535 pour réussir
un de ces concours contre un élève de Scipione del Ferro afin d'obtenir un poste dans une université que Tartaglia aurait redécouvert
la méthode générale pour résoudre une équation de ce type.
Un autre mathématicien italien Jérôme Cardan l'aurait reçu de Tartaglia sous réserve de garder cette formule secrète. Ayant appris que Scipione del Ferro l'aurait découverte avant Tartaglia, il se sentit dégagé de sa promesse et publia en 1545 cette méthode dans un ouvrage nommé Ars Magna. Cette méthode s'appelle dès lors la méthode de Cardan-Tartaglia ou la méthode de Del Ferro-Tartaglia.
Raphaël Bombelli a proposé les calculs sur les nombres appelés depuis nombres complexes pour obtenir une généralisation de cette méthode au cas où $\Delta=\dfrac{27q^2+4p^3}{27}<0$.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International