Le cours complet avec les exercices du chapitre est disponible en version imprimable en cliquant ici.
Demander le programme !

Définition
Matrice
On appelle matrice $n\times p$ tout tableau de nombres ayant $n$ lignes et $p$ colonnes.
On dit que la matrice est carrée si $n=p$. On parle de matrice d'ordre $n$
On note $A=(a_{ij})_{1\leq i \leq n \textrm{ et } 1\leq j \leq p }$ la matrice :
$A= \begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1j}&\ldots&a_{1p}\\ a_{21}&a_{22}&\ldots&a_{2j}&\ldots&a_{2p}\\ \vdots&&&\vdots&&\vdots\\ a_{i1}&\vdots&\vdots&a_{ij}&\ldots&a_{ip}\\ \vdots&&&\vdots&&\vdots\\ a_{n1}&a_{n2}&\ldots&a_{nj}&\ldots&a_{np}\\ \end{pmatrix}$
où $a_{ij}$ se situe à la ligne $i$ et à la ligne $j$.
La matrice
$A= \begin{pmatrix} -2&1 \\ 0&\sqrt{2}\\ \pi&12 \end{pmatrix}$
est une matrice $3\times 2$.
Ensemble de matrices
-
L'ensemble des matrices à coefficients réels à $n$ lignes et $p$ colonnes est noté $\mathcal{M}_{n,p}(\mathbb{R})$.
-
L'ensemble des matrices carrées à coefficients réels à $n$ lignes et $n$ colonnes est noté $\mathcal{M}_{n}(\mathbb{R})$.
- La matrice de l'exemple précédent est une matrice de $\mathcal{M}_{3,2}(\mathbb{R})$
- $A= \begin{pmatrix} -2&1&2 \\ 0&\sqrt{2}&-5\\ \pi&12&3 \end{pmatrix}$ est une matrice carrée de $\mathcal{M}_{3}(\mathbb{R})$
Deux matrices $A$ et $B$ sont égales si, et seulement si $a_{ij}=b_{ij}$ pour tout $i$ et $j$.
L'égalité de deux matrices ne peut intervenir que si elles sont de même taille.
Déterminer $x$ et $y$ réels, s'ils existent, tels que :
$\begin{pmatrix} x+y&3\\ 2&2x-y\\ \end{pmatrix}=\begin{pmatrix} 1&3\\ 2&2\\ \end{pmatrix}$
Opération sur les matrices
Somme
Addition
Soient $A$ et $B$ de $\mathcal{M}_{np}(\mathbb{R})$.
La matrice somme $C=A+B$ est la matrice de $\mathcal{M}_{np}(\mathbb{R})$ tel que $c_{ij}=a_{ij}+b_{ij}$
$\begin{pmatrix} 0&1&-5\\ 5&12&3 \end{pmatrix}+\begin{pmatrix} 1&-2&5\\ 3&2&1 \end{pmatrix}=$
Multiplication par un scalaire
multiplication par un scalaire
Soit $A$ de $\mathcal{M}_{np}(\mathbb{R})$ et $\lambda$ un réel.
La matrice $B=\lambda \times A$ est la matrice de $\mathcal{M}_{np}(\mathbb{R})$ tel que $b_{ij}=\lambda\times a_{ij}$
$-2\times\begin{pmatrix} 5&-1 \\ 1&5\\ 3&2 \end{pmatrix}=$
soustraction de deux matrices
Soustraction
Soient $A$ et $B$ de $\mathcal{M}_{np}(\mathbb{R})$.
La matrice différence $C=A-B$ est la matrice $A+(-1)\times B$
$\begin{pmatrix} -2&2 \\ 0&1\\ 5&3 \end{pmatrix}-\begin{pmatrix} 5&-1 \\ 1&5\\ 3&2 \end{pmatrix}=$
Produit de deux matrices
Une usine fabrique trois sortes d’articles : $a1$, $a2$ et $a3$ à partir de trois modules : $m1$, $m2$ et $m3$. On donne :
Articles
Modules
$a1$
$a2$
$a3$
$m1$
3
9
5
$m2$
4
0
9
$m3$
4
8
6
Modules
$m1$
$m2$
$m3$
5
6
3
Masse unitaire en kilogramme
180
250
150
Coûts unitaires en euros
Explications : pour fabriquer un article $a2$, il faut 9 modules $m1$ et 8 modules $m3$. Un module $m1$ pèse 5kg et coûte 180 euros.
-
Calculer la masse d’un article $a1$ sachant qu’il n’est construit qu’à partir des modules $m1$, $m2$ et $m3$.
-
Calculer les coûts unitaires (en euro) liés aux composants pour fabriquer un article $a1$.
-
Compléter le tableau suivant :
Articles
$a1$
$a2$
$a3$
...
...
...
Masse unitaire en kilogramme
...
...
...
Coûts unitaires en euros
-
-
Le premier tableau de l'exercice, celui qui lie chaque article aux modules nécessaires à sa fabrication est associée à une matrice $B$.
Déterminer cette matrice $B$.
-
Le deuxième tableau de l'exercice, celui qui lie chaque module à une masse et un coût est associée à une matrice $A$.
Déterminer cette matrice $A$.
-
Le dernier tableau de l'exercice, celui obtenu à la question précédente, est associée à une matrice $C$.
Déterminer cette matrice $C$.
L’ensemble des opérations faites pour obtenir ce tableau correspondent à ce que l’on appelle la multiplication entre deux matrices.
Ainsi, cette nouvelle matrice est notée $A\times B$ ou simplement $AB$.
On peut visualiser l'ensemble des opérations liées à la multiplication avec le schéma suivant :
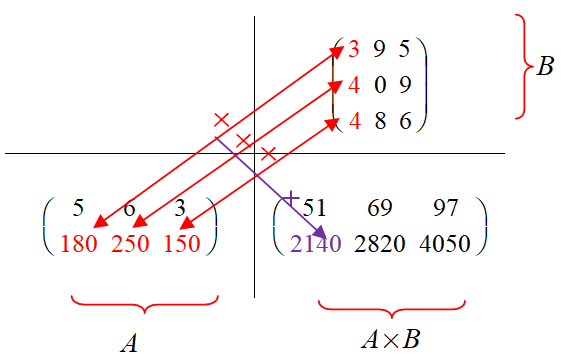
Multiplication matricielle
Soient $A\in\mathcal{M}_{mn}(\mathbb{R})$ et $B\in\mathcal{M}_{np}(\mathbb{R})$.
La matrice produit $C=A\times B$ est la matrice de $\mathcal{M}_{mp}(\mathbb{R})$ $C=A\times B$ tel que $c_{ij}=\sum\limits_{k=1}^{n}a_{ik}\times b_{kj}$
Attention : La multiplication d'une matrice $A$ par une matrice $B$ ($A\times B$) n'est possible que si le nombre de colonnes de la matrice
$A$ est égal au nombre de lignes de $B$.
Soient $A=\begin{pmatrix} 1&-1&4 \\ 1&5&3\\ 2&3&4 \end{pmatrix}$, $B=\begin{pmatrix} 8&4&-6 \\ 2&3&1\\ 0&-2&-5 \end{pmatrix}$
et $C=AB$
Démontrer que $c_{32}=9$.
- $\begin{pmatrix} -2&1&2 \\ 0&1&-5\\ 5&12&3 \end{pmatrix}\times \begin{pmatrix} 5&-1&3 \\ 1&-2&5\\ 3&2&1 \end{pmatrix}$
$\begin{pmatrix} -2&1&2 \\ 5&12&3\\ \end{pmatrix}\times \begin{pmatrix} -1&3 \\ 2&0\\ 3&2 \end{pmatrix}$
Voici un test de deux questions portant sur les bases du calcul matriciel.
Cas particuliers des matrices carrées
Propriétés algébriques des matrices carrées
Soient $A$, $B$ , $C$ et $D$ quatre matrices de $\mathcal{M}_{n}(\mathbb{R})$.
- $A(BC)=(AB)C=ABC$
- $A(B+C)=AB+AC$
- $(B+C)A=BA+CA$
- $(A+B)(C+D)=AC+AD+BC+BD$
Soit $A=\begin{pmatrix} 1&2 \\ 3&4 \end{pmatrix}$ et $B=\begin{pmatrix} 2&0 \\ 3&1 \end{pmatrix}$
-
Calculer $AB$
-
Calculer $BA$
-
Que dire ?
La multiplication matricielle n'est pas commutative. C'est à dire que de manière générale $AB\ne BA$.
Soit $A=\begin{pmatrix} 1&0 \\ 0&0 \end{pmatrix}$ et $B=\begin{pmatrix} 0&0 \\ 0&1 \end{pmatrix}$
-
Calculer $AB$
-
Que dire ?
La multiplication matricielle n'est pas intègre. C'est à dire que de manière générale $AB=0$ ne donne pas $A=0$ ou $B=0$.
Soit $A=\begin{pmatrix} 1&2 \\ 2&4 \end{pmatrix}$ ; $B=\begin{pmatrix} 2&-6 \\ -1&3 \end{pmatrix}$ et $C=\begin{pmatrix} -2&10 \\ 1&-5 \end{pmatrix}$
-
Calculer $AB$
-
Calculer $AC$
-
Que dire ?
Matrice identité et inverse
Matrice identité
On appelle matrice identité la matrice $I_{n}\in\mathcal{M}_{n}(\mathbb{R})$ tel que $i_{ii}=1$ et $i_{ij}=0$ si $i\ne j$.
$I_n=\begin{pmatrix} 1&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&1 \end{pmatrix}$
Pour tout $A\in\mathcal{M}_{n}(\mathbb{R})$, $A\times I_n=I_n\times A=A$
Matrice inverse
Soit $A\in\mathcal{M}_{n}(\mathbb{R})$, s'il existe $B\in\mathcal{M}_{n}(\mathbb{R})$ telle que $AB=BA=I_n$, alors on dit que $A$ est
inversible et B est la matrice inverse de $A$ on la note $A^{-1}$.
On donne $A=\begin{pmatrix} 1&2&-1 \\ 1&0&2\\ -1&2&-1 \end{pmatrix}$ et $B=\frac18\begin{pmatrix} 4&0&-4\\ 1&2&3\\ -2&4&2\\ \end{pmatrix}$
Montrer que $B=A^{-1}$
$A=\begin{pmatrix} 0&1 \\ -1&0 \end{pmatrix}$ Calculer $A^2$, $A^3$ et $A^4$. En déduire $A^{-1}$.
Inverse des matrices carrées d'ordre 2
Soit $A=\begin{pmatrix} a&b \\ c&d \end{pmatrix}$ .
On note $det(A)=ad-bc$ appelé déterminant de $A$.
$A$ est inversible si, et seulement si, $det(A)\ne 0$.
De plus, dans ce cas, $A^{-1}=\dfrac{1}{det(A)}\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$.
-
Posons $B=\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$?
-
Démonter que $AB=BA=det(A)I_2$.
-
En déduire que si $det(A)\neq 0$ alors $A$est inversible et $A^{-1}=\dfrac{1}{det(A)}\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$.
Supposons que $A$ est inversible.
-
Démontrer que $B=\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$ vérifie alors : $B=det(A)A^{-1}$.
Utiliser le 1.a.
-
En déduire que $det(A)\neq0$.
On considère le système $(S): \left \{ \begin{array}{c c} x+2y & =1 \\ 3x-4y &=2 \\ \end{array} \right.$
On pose $A=\begin{pmatrix} 1&2\\ 3&-4 \end{pmatrix}$; $X=\begin{pmatrix} x\\ y \end{pmatrix}$ et $B=\begin{pmatrix} 1\\ 2 \end{pmatrix}$
-
Déterminer $A^{-1}$.
-
Vérifier que $(S)$ peut s'écrire $AX=B$
-
En déduire les solutions du système.
Voici un test de trois questions portant sur l'inverse d'une matrice
et l'utilisation de matrices pour résoudre un système.
Matrice diagonale
Matrice diagonale
On appelle matrice diagonale la matrice $A\in\mathcal{M}_{n}(\mathbb{R})$ tel que $a_{ij}=0$ si $i\ne j$.
On dit aussi que tous les coefficients sont nuls sauf ceux de la diagonale principale}.
$A=\begin{pmatrix} a_{11}&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&a_{nn} \end{pmatrix}$
Soit $A$ une matrice diagonale d'ordre $n$ alors, pour tout entier naturel $k$ non nul, on a :
$A^k=\begin{pmatrix} a_{11}^k&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&a_{nn}^k \end{pmatrix}$
Quel raisonnement permet de démontrer ce résultat ?
Le but de cet exercice est de voir comment on peut calculer avec des matrices en Python.
Les modules numpy et numpy.linalg permettent de travailler avec des matrices en Python
-
Saisir le code suivant :
from numpy import *
from numpy.linalg import *
A=array([[2,0,0],[0,3,0],[0,0,0.5]])
B=array([[1],[4],[7]])
C=array([[1,2],[3,-4]])
Quel est le rôle de la fonction array ?
-
Vérifier que l'addition est obtenue avec +.
-
Exécuter dot(A,B).
Quelle opération correspond à ce calcul ?
-
Exécuter det(C) et inv(C).
Quel est le rôle des fonctions det et inv ?
-
Exécuter matrix_power(A,3).
Quel est le rôle de la fonction matrix_power ?
Application du calcul matriciel aux graphes.
Nombre de chemins de longueur $k$
Soient $n$ et $k$ deux entiers naturels non nuls et $M$ la matrice d'adjacence d'un graphe d'ordre $n$, dont les sommets sont numérotés de 1 à $n$ et rangés dans l'ordre croissant.
Le terme positionné en ligne $i$ et en colonne $j$ de la matrice $M^k$ donne le nombre de chaînes ( ou de chemins) de longueur $k$ reliant le sommet $i$ au sommet $j$.
Démonstration
Soit $M=(a_{ij})_{1\leq i \leq n, 1\leq j\leq n}=
\begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1n} \\ a_{21}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&a_{n-1n}\\ a_{n1}&\ldots&a_{nn-1}&a_{nn} \end{pmatrix}$
Nous allons démontrer ce résultat par récurrence.
On définit, pour $k\in\mathbb{N}^*$, $P(k)$:"Le coefficient $b_{ij}$ de la matrice $M^k$ est le nombre de chemins( ou chaînes) reliant $i$ à $j$"
-
Vérifier que la propriété est vraie au range $k=1$.
-
Soit $k\in\mathbb{N}^*$, supposons $P(k)$. On note $M^{k+1}=(c_{ij})_{(i,j)\in[|1;n|]}$
-
Donner une expression reliant les coefficients des matrices $M$, $M^k$ et $M^{k+1}$.
-
Interpréter $b_{il}a_{lj}$ en terme de nombres de chaînes, $i$, $l$ et $j$ sont trois entiers compris entre 1 et $n$.
-
En déduire que $c_{ij}$ est le nombre de chaînes de longueur $k+1$ reliant les sommets $i$ à $j$.
- Conclure.
On considère un graphe dont la matrice d'adjacence obtenue en numérotant les sommets de 1 à 5 est :
$M=\begin{pmatrix} 1&0&1&0&1\\1&0&1&1&1\\0&1&0&0&1\\1&1&0&1&1\\0&1&1&1&1 \end{pmatrix}$
-
Donner le nombre de chaînes de longueur 2 permettant d'aller du sommet n°3 au sommet n°5.
-
Donner le nombre de chaînes de longueur 2 permettant d'aller du sommet n°1 au sommet n°4.
-
Est-il vrai qu'il y a plus d'un million de chaînes de longueur 12 permettant d'aller du sommet n°4 au sommet n°5 ? Justifier.
Voici un test de deux questions portant sur les puissances d'une
matrice et de leur utilisation pour l'étude de graphes.
Matrices et transformations du plan
Matrice
On appelle matrice $n\times p$ tout tableau de nombres ayant $n$ lignes et $p$ colonnes.
On dit que la matrice est carrée si $n=p$. On parle de matrice d'ordre $n$
On note $A=(a_{ij})_{1\leq i \leq n \textrm{ et } 1\leq j \leq p }$ la matrice :
$A= \begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1j}&\ldots&a_{1p}\\ a_{21}&a_{22}&\ldots&a_{2j}&\ldots&a_{2p}\\ \vdots&&&\vdots&&\vdots\\ a_{i1}&\vdots&\vdots&a_{ij}&\ldots&a_{ip}\\ \vdots&&&\vdots&&\vdots\\ a_{n1}&a_{n2}&\ldots&a_{nj}&\ldots&a_{np}\\ \end{pmatrix}$où $a_{ij}$ se situe à la ligne $i$ et à la ligne $j$.
La matrice
$A= \begin{pmatrix} -2&1 \\ 0&\sqrt{2}\\ \pi&12 \end{pmatrix}$est une matrice $3\times 2$.
Ensemble de matrices
-
L'ensemble des matrices à coefficients réels à $n$ lignes et $p$ colonnes est noté $\mathcal{M}_{n,p}(\mathbb{R})$.
-
L'ensemble des matrices carrées à coefficients réels à $n$ lignes et $n$ colonnes est noté $\mathcal{M}_{n}(\mathbb{R})$.
- La matrice de l'exemple précédent est une matrice de $\mathcal{M}_{3,2}(\mathbb{R})$
- $A= \begin{pmatrix} -2&1&2 \\ 0&\sqrt{2}&-5\\ \pi&12&3 \end{pmatrix}$ est une matrice carrée de $\mathcal{M}_{3}(\mathbb{R})$
Deux matrices $A$ et $B$ sont égales si, et seulement si $a_{ij}=b_{ij}$ pour tout $i$ et $j$.
L'égalité de deux matrices ne peut intervenir que si elles sont de même taille.
Déterminer $x$ et $y$ réels, s'ils existent, tels que :
$\begin{pmatrix} x+y&3\\ 2&2x-y\\ \end{pmatrix}=\begin{pmatrix} 1&3\\ 2&2\\ \end{pmatrix}$
Addition
Soient $A$ et $B$ de $\mathcal{M}_{np}(\mathbb{R})$.
La matrice somme $C=A+B$ est la matrice de $\mathcal{M}_{np}(\mathbb{R})$ tel que $c_{ij}=a_{ij}+b_{ij}$
$\begin{pmatrix} 0&1&-5\\ 5&12&3 \end{pmatrix}+\begin{pmatrix} 1&-2&5\\ 3&2&1 \end{pmatrix}=$
multiplication par un scalaire
Soit $A$ de $\mathcal{M}_{np}(\mathbb{R})$ et $\lambda$ un réel.
La matrice $B=\lambda \times A$ est la matrice de $\mathcal{M}_{np}(\mathbb{R})$ tel que $b_{ij}=\lambda\times a_{ij}$
$-2\times\begin{pmatrix} 5&-1 \\ 1&5\\ 3&2 \end{pmatrix}=$
Soustraction
Soient $A$ et $B$ de $\mathcal{M}_{np}(\mathbb{R})$.
La matrice différence $C=A-B$ est la matrice $A+(-1)\times B$
$\begin{pmatrix} -2&2 \\ 0&1\\ 5&3 \end{pmatrix}-\begin{pmatrix} 5&-1 \\ 1&5\\ 3&2 \end{pmatrix}=$
Une usine fabrique trois sortes d’articles : $a1$, $a2$ et $a3$ à partir de trois modules : $m1$, $m2$ et $m3$. On donne :
|
Articles |
||||
| Modules | $a1$ | $a2$ | $a3$ | |
| $m1$ | 3 | 9 | 5 | |
| $m2$ | 4 | 0 | 9 | |
| $m3$ | 4 | 8 | 6 |
| Modules | |||
| $m1$ | $m2$ | $m3$ | |
| 5 | 6 | 3 | Masse unitaire en kilogramme |
| 180 | 250 | 150 | Coûts unitaires en euros |
Explications : pour fabriquer un article $a2$, il faut 9 modules $m1$ et 8 modules $m3$. Un module $m1$ pèse 5kg et coûte 180 euros.
-
Calculer la masse d’un article $a1$ sachant qu’il n’est construit qu’à partir des modules $m1$, $m2$ et $m3$.
-
Calculer les coûts unitaires (en euro) liés aux composants pour fabriquer un article $a1$.
-
Compléter le tableau suivant :
Articles $a1$ $a2$ $a3$ ... ... ... Masse unitaire en kilogramme ... ... ... Coûts unitaires en euros -
-
Le premier tableau de l'exercice, celui qui lie chaque article aux modules nécessaires à sa fabrication est associée à une matrice $B$. Déterminer cette matrice $B$.
-
Le deuxième tableau de l'exercice, celui qui lie chaque module à une masse et un coût est associée à une matrice $A$. Déterminer cette matrice $A$.
-
Le dernier tableau de l'exercice, celui obtenu à la question précédente, est associée à une matrice $C$. Déterminer cette matrice $C$.
-
L’ensemble des opérations faites pour obtenir ce tableau correspondent à ce que l’on appelle la multiplication entre deux matrices.
Ainsi, cette nouvelle matrice est notée $A\times B$ ou simplement $AB$.
On peut visualiser l'ensemble des opérations liées à la multiplication avec le schéma suivant :

Multiplication matricielle
Soient $A\in\mathcal{M}_{mn}(\mathbb{R})$ et $B\in\mathcal{M}_{np}(\mathbb{R})$.
La matrice produit $C=A\times B$ est la matrice de $\mathcal{M}_{mp}(\mathbb{R})$ $C=A\times B$ tel que $c_{ij}=\sum\limits_{k=1}^{n}a_{ik}\times b_{kj}$
Attention : La multiplication d'une matrice $A$ par une matrice $B$ ($A\times B$) n'est possible que si le nombre de colonnes de la matrice $A$ est égal au nombre de lignes de $B$.
Soient $A=\begin{pmatrix} 1&-1&4 \\ 1&5&3\\ 2&3&4 \end{pmatrix}$, $B=\begin{pmatrix} 8&4&-6 \\ 2&3&1\\ 0&-2&-5 \end{pmatrix}$ et $C=AB$
Démontrer que $c_{32}=9$.
- $\begin{pmatrix} -2&1&2 \\ 0&1&-5\\ 5&12&3 \end{pmatrix}\times \begin{pmatrix} 5&-1&3 \\ 1&-2&5\\ 3&2&1 \end{pmatrix}$
Voici un test de deux questions portant sur les bases du calcul matriciel.
Soient $A$, $B$ , $C$ et $D$ quatre matrices de $\mathcal{M}_{n}(\mathbb{R})$.
- $A(BC)=(AB)C=ABC$
- $A(B+C)=AB+AC$
- $(B+C)A=BA+CA$
- $(A+B)(C+D)=AC+AD+BC+BD$
Soit $A=\begin{pmatrix} 1&2 \\ 3&4 \end{pmatrix}$ et $B=\begin{pmatrix} 2&0 \\ 3&1 \end{pmatrix}$
-
Calculer $AB$
-
Calculer $BA$
-
Que dire ?
Soit $A=\begin{pmatrix} 1&0 \\ 0&0 \end{pmatrix}$ et $B=\begin{pmatrix} 0&0 \\ 0&1 \end{pmatrix}$
-
Calculer $AB$
-
Que dire ?
intègre. C'est à dire que de manière générale $AB=0$ ne donne pas $A=0$ ou $B=0$.Soit $A=\begin{pmatrix} 1&2 \\ 2&4 \end{pmatrix}$ ; $B=\begin{pmatrix} 2&-6 \\ -1&3 \end{pmatrix}$ et $C=\begin{pmatrix} -2&10 \\ 1&-5 \end{pmatrix}$
-
Calculer $AB$
-
Calculer $AC$
-
Que dire ?
Matrice identité
On appelle matrice identité la matrice $I_{n}\in\mathcal{M}_{n}(\mathbb{R})$ tel que $i_{ii}=1$ et $i_{ij}=0$ si $i\ne j$.
$I_n=\begin{pmatrix} 1&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&1 \end{pmatrix}$
Pour tout $A\in\mathcal{M}_{n}(\mathbb{R})$, $A\times I_n=I_n\times A=A$
Matrice inverse
Soit $A\in\mathcal{M}_{n}(\mathbb{R})$, s'il existe $B\in\mathcal{M}_{n}(\mathbb{R})$ telle que $AB=BA=I_n$, alors on dit que $A$ est inversible et B est la matrice inverse de $A$ on la note $A^{-1}$.
On donne $A=\begin{pmatrix} 1&2&-1 \\ 1&0&2\\ -1&2&-1 \end{pmatrix}$ et $B=\frac18\begin{pmatrix} 4&0&-4\\ 1&2&3\\ -2&4&2\\ \end{pmatrix}$
Montrer que $B=A^{-1}$
$A=\begin{pmatrix} 0&1 \\ -1&0 \end{pmatrix}$ Calculer $A^2$, $A^3$ et $A^4$. En déduire $A^{-1}$.
Soit $A=\begin{pmatrix} a&b \\ c&d \end{pmatrix}$ .
On note $det(A)=ad-bc$ appelé déterminant de $A$.
$A$ est inversible si, et seulement si, $det(A)\ne 0$.
De plus, dans ce cas, $A^{-1}=\dfrac{1}{det(A)}\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$.
-
Posons $B=\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$?
-
Démonter que $AB=BA=det(A)I_2$.
-
En déduire que si $det(A)\neq 0$ alors $A$est inversible et $A^{-1}=\dfrac{1}{det(A)}\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$.
-
Supposons que $A$ est inversible.
-
Démontrer que $B=\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$ vérifie alors : $B=det(A)A^{-1}$.
Utiliser le 1.a.
-
En déduire que $det(A)\neq0$.
On considère le système $(S): \left \{ \begin{array}{c c} x+2y & =1 \\ 3x-4y &=2 \\ \end{array} \right.$ On pose $A=\begin{pmatrix} 1&2\\ 3&-4 \end{pmatrix}$; $X=\begin{pmatrix} x\\ y \end{pmatrix}$ et $B=\begin{pmatrix} 1\\ 2 \end{pmatrix}$
-
Déterminer $A^{-1}$.
-
Vérifier que $(S)$ peut s'écrire $AX=B$
-
En déduire les solutions du système.
Voici un test de trois questions portant sur l'inverse d'une matrice et l'utilisation de matrices pour résoudre un système.
Matrice diagonale
On appelle matrice diagonale la matrice $A\in\mathcal{M}_{n}(\mathbb{R})$ tel que $a_{ij}=0$ si $i\ne j$.
On dit aussi que tous les coefficients sont nuls sauf ceux de la diagonale principale}.
$A=\begin{pmatrix} a_{11}&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&a_{nn} \end{pmatrix}$
Soit $A$ une matrice diagonale d'ordre $n$ alors, pour tout entier naturel $k$ non nul, on a : $A^k=\begin{pmatrix} a_{11}^k&0&\ldots&0 \\ 0&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&0\\ 0&\ldots&0&a_{nn}^k \end{pmatrix}$
Quel raisonnement permet de démontrer ce résultat ?
Le but de cet exercice est de voir comment on peut calculer avec des matrices en Python.
Les modules numpy et numpy.linalg permettent de travailler avec des matrices en Python
-
Saisir le code suivant :
from numpy import * from numpy.linalg import * A=array([[2,0,0],[0,3,0],[0,0,0.5]]) B=array([[1],[4],[7]]) C=array([[1,2],[3,-4]])Quel est le rôle de la fonction
array? -
Vérifier que l'addition est obtenue avec
+. -
Exécuter
dot(A,B).
Quelle opération correspond à ce calcul ? -
Exécuter
det(C)etinv(C).
Quel est le rôle des fonctionsdetetinv? -
Exécuter
matrix_power(A,3).
Quel est le rôle de la fonctionmatrix_power?
Nombre de chemins de longueur $k$
Soient $n$ et $k$ deux entiers naturels non nuls et $M$ la matrice d'adjacence d'un graphe d'ordre $n$, dont les sommets sont numérotés de 1 à $n$ et rangés dans l'ordre croissant.
Le terme positionné en ligne $i$ et en colonne $j$ de la matrice $M^k$ donne le nombre de chaînes ( ou de chemins) de longueur $k$ reliant le sommet $i$ au sommet $j$.
Démonstration
Soit $M=(a_{ij})_{1\leq i \leq n, 1\leq j\leq n}= \begin{pmatrix} a_{11}&a_{12}&\ldots&a_{1n} \\ a_{21}&\ddots&\ddots&\vdots\\ \vdots&\ddots&\ddots&a_{n-1n}\\ a_{n1}&\ldots&a_{nn-1}&a_{nn} \end{pmatrix}$
Nous allons démontrer ce résultat par récurrence.
On définit, pour $k\in\mathbb{N}^*$, $P(k)$:"Le coefficient $b_{ij}$ de la matrice $M^k$ est le nombre de chemins( ou chaînes) reliant $i$ à $j$"
-
Vérifier que la propriété est vraie au range $k=1$.
-
Soit $k\in\mathbb{N}^*$, supposons $P(k)$. On note $M^{k+1}=(c_{ij})_{(i,j)\in[|1;n|]}$
-
Donner une expression reliant les coefficients des matrices $M$, $M^k$ et $M^{k+1}$.
-
Interpréter $b_{il}a_{lj}$ en terme de nombres de chaînes, $i$, $l$ et $j$ sont trois entiers compris entre 1 et $n$.
-
En déduire que $c_{ij}$ est le nombre de chaînes de longueur $k+1$ reliant les sommets $i$ à $j$.
-
- Conclure.
On considère un graphe dont la matrice d'adjacence obtenue en numérotant les sommets de 1 à 5 est :
$M=\begin{pmatrix} 1&0&1&0&1\\1&0&1&1&1\\0&1&0&0&1\\1&1&0&1&1\\0&1&1&1&1 \end{pmatrix}$
-
Donner le nombre de chaînes de longueur 2 permettant d'aller du sommet n°3 au sommet n°5.
-
Donner le nombre de chaînes de longueur 2 permettant d'aller du sommet n°1 au sommet n°4.
-
Est-il vrai qu'il y a plus d'un million de chaînes de longueur 12 permettant d'aller du sommet n°4 au sommet n°5 ? Justifier.
Voici un test de deux questions portant sur les puissances d'une matrice et de leur utilisation pour l'étude de graphes.
Dans toute cette partie, on se place dans un plan orthonormé direct $(O ; \overrightarrow{i}, \overrightarrow{j})$.
Tout point $M$ du plan a des coordonnées $(x;y)$. Ces coordonnées
peuvent être écrites sous forme de matrice colonne :
$\begin{pmatrix}x \\ y\end{pmatrix}$.
De même, tout vecteur $\overrightarrow{u}$ du plan a des coordonnées
$(x;y)$. Ces coordonnées
peuvent être écrite sous forme de matrice colonne :
$\begin{pmatrix}x \\ y\end{pmatrix}$.
On considère la translation de vecteur $\overrightarrow{T}$, de coordonnées
$\begin{pmatrix}T_1 \\ T_2\end{pmatrix}$.
À tout point $M$ de coordonnées $\begin{pmatrix}x_M \\ y_M\end{pmatrix}$,
cette translation associe le point $N$ de coordonnées
$\begin{pmatrix}x_N \\ y_N\end{pmatrix}$ tel que $\overrightarrow{MN}=\overrightarrow{T}$.
Cette translation peut être écrit d'un point de vue matriciel comme la somme
des matrices colonnes :
$\begin{pmatrix}x_N \\ y_N\end{pmatrix}=\begin{pmatrix}x_M \\ y_M\end{pmatrix}+\begin{pmatrix}T_1 \\ T_2\end{pmatrix}$.
Toutes les transformations géométriques du plan suivantes associent
à tout point $M$ de coordonnées $\begin{pmatrix}x_M \\ y_M\end{pmatrix}$,
le point $N$ de coordonnées $\begin{pmatrix}x_N \\ y_N\end{pmatrix}$.
Toutes les transformations suivantes peuvent être
décrites d'un point de vue matriciel comme le produit avec une matrice carrée
$\begin{pmatrix}a&b\\c&d\end{pmatrix}$ :
-
La symétrie axiale par rapport à l'axe des abscisses peut être écrite comme $\begin{pmatrix}x_N \\ y_N\end{pmatrix}=\begin{pmatrix}1&0\\0&-1\end{pmatrix}\times \begin{pmatrix}x_M\\y_M\end{pmatrix}$.
-
La symétrie axiale par rapport à l'axe des ordonnées peut être écrite comme $\begin{pmatrix}x_N \\ y_N\end{pmatrix}=\begin{pmatrix}-1&0\\0&1\end{pmatrix}\times \begin{pmatrix}x_M\\y_M\end{pmatrix}$.
-
La rotation de centre l'origine $O$ et d'angle $\theta$ peut être écrite comme $\begin{pmatrix}x_N \\ y_N\end{pmatrix}=\begin{pmatrix}\cos(\theta)&-\sin(\theta)\\ \sin(\theta)&\cos(\theta)\end{pmatrix}\times \begin{pmatrix}x_M\\y_M\end{pmatrix}$.
-
L'homothétie de centre l'origine $O$ et de rapport $k\in\mathbb{R}$ peut être écrite comme $\begin{pmatrix}x_N \\ y_N\end{pmatrix}=\begin{pmatrix}k&0\\0&k\end{pmatrix}\times \begin{pmatrix}x_M\\y_M\end{pmatrix}$.
La matrice $\begin{pmatrix}0&-1\\1&0\end{pmatrix}$ est la matrice associée à la rotation de centre $O$ et d'angle $\dfrac{\pi}{2}$ car $\cos\left(\dfrac{\pi}{2}\right) =0$ et $\sin\left(\dfrac{\pi}{2}\right) =1$.
Pour chacune des transformations ci-dessous, déterminer la matrice de transformation associée.
-
La transformation qui transforme le carré violet en celui bleu :
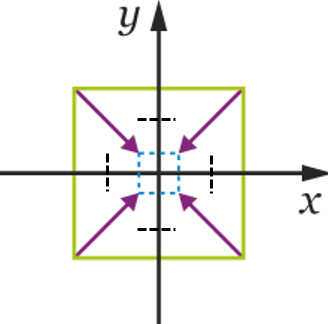
-
La transformation qui transforme le carré bleu en pointillés en celui vert :
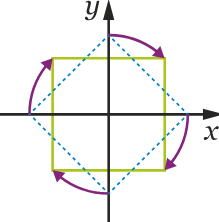
-
La transformation qui transforme le triangle vert en celui bleu :
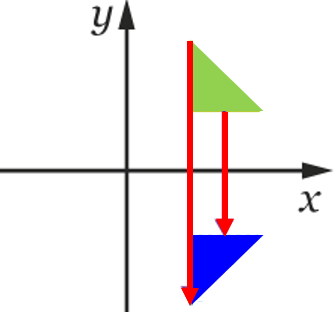
-
La transformation qui transforme le triangle bleu en celui vert :
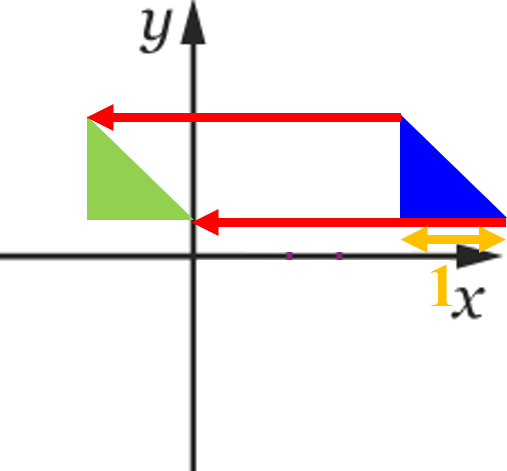
-
La transformation qui transforme le triangle vert en celui bleu :
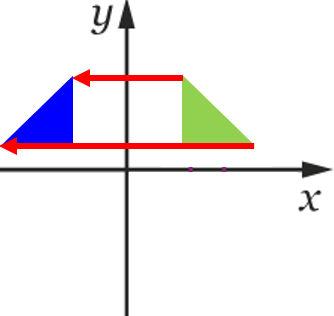
-
Déterminer la transformation associée à la matrice $\begin{pmatrix}-\dfrac{1}{2}&\dfrac{\sqrt{3}}{2}\\ -\dfrac{\sqrt{3}}{2}& -\dfrac{1}{2}\end{pmatrix}$.
-
Le point $M$ de coordonnées $\begin{pmatrix}1 \\ 2\end{pmatrix}$ subit les trois transformations successives suivantes :
-
la translation de vecteur $\begin{pmatrix}-3 \\4\end{pmatrix}$,
-
la rotation de centre $O$ et d'angle $\dfrac{\pi}{6}$,
-
l'homothétie de de centre $O$ et de rapport $-5$.
Déterminer les coordonnées de l'image $N$ du point $M$ à l'issue de ces trois transformations.
-
Suites de matrices
Dans toute cette partie, $N$ désigne un entier naturel supérieur ou égal à $2$.
On considère une suite de matrices colonnes $\left(U_n\right)$ ayant $N$ lignes.
On suppose que cette suite est définie par son premier terme $U_0$ (une matrice colonne
à $N$ lignes) et pour tout entier naturel $n$ par la relation de récurrence
$U_{n+1}=AU_n+C$, où $A$ est une matrice carrée d'ordre $N$ et $C$ une matrice colonne
ayant $N$ lignes.
On appelle état stable de la suite $(U_n)$ une matrice colonne $S$ ayant $N$ lignes telles que $S=AS+C$.
On considère la suite $(U_n)$ définie par $U_0=\begin{pmatrix}\pi\\ e^2 \\ 4 \end{pmatrix}$ et pour tout entier naturel $n$ par $U_{n+1}=AU_n+C$ avec $A=\begin{pmatrix}0&0&1\\0.5&0&0\\0.5&1&0 \end{pmatrix}$ et $C=\begin{pmatrix}1\\ 0 \\ -1 \end{pmatrix}$
Quel que soit le réel $x$, la matrice $S=\begin{pmatrix}x\\ 0.5x \\ x-1 \end{pmatrix}$ est un état stable de la suite $(U_n)$ car $AS=\begin{pmatrix}x-1\\ 0.5x \\ x \end{pmatrix}$ donc $AS+C=\begin{pmatrix}x\\ 0.5x \\ x-1 \end{pmatrix}=S$
Si la matrice $I_N-A$ est inversible, alors il existe
un unique état stable $S$.
De plus, cet état stable est donné par $S=(I_N-A)^{-1}C$.
$S=AS+C \iff S-AS=C$ $\iff (I_N-A)S=C$.
Si la matrice $I_N-A$ est inversible, alors $(I_N-A)^{-1}$ existe.
De plus, $(I_N-A)S=C$ $\iff (I_N-A)^{-1}(I_N-A)S=(I_N-A)^{-1}C$
soit $S=(I_N-A)^{-1}C$.
Dans une forêt arctique vivent des lièvres arctiques et des lynx.
Les lynx se nourrissent presque exclusivement de lièvres.
En tenant compte des prélèvements dus à la chasse et aux venues depuis les forêts voisines,
chaque année 30 lièvres et 2 lynx arrivent dans cette forêt.
En 2025, cette forêt contient 430 lièvres et 90 lynx.
On note $u_n$ le nombre de lièvres et $v_n$ le nombre de lynx
présents dans cette forêt au bout de $n$ années après 2025.
On admet que la population de lièvres et de lynx suit le modèle suivant,
dit modèle de proies-prédateurs, suivant :
$\left \{ \begin{array}{l l} u_{n+1}& =\dfrac{9}{10} u_n-\dfrac{3}{10}v_n+30 \\
v_{n+1}& =\dfrac{1}{10}u_n+\dfrac{1}{2} v_n+2 \end{array} \right.$.
On pose $U_n=\begin{pmatrix}u_n\\v_n\end{pmatrix}$.
Partie A : détermination d'un état stable
-
Déterminer les matrices $A$ et $C$ telles que le système $\left \{ \begin{array}{l l} u_{n+1}& =\dfrac{9}{10} u_n-\dfrac{3}{10}v_n+30 \\ v_{n+1}& =\dfrac{1}{10}u_n+\dfrac{1}{2} v_n+2 \end{array} \right.$ s'écrive d'un point de vue matriciel sous la forme $U_{n+1}=AU_n+C$.
-
Déterminer les termes de $U_0$.
-
Déterminer $U_1$.
-
Déterminer le nombres de lièvres et de lynx prévus par le modèle dans cette forêt en 2027.
-
Compléter le programme suivant en Python de sorte que
U(n)renvoie le couple de valeurs de $U_n$ :def U(n): u = ... v = ... for i in range(...): temp = ... v = ... u = ... return (u, v) -
Démontrer que la matrice $I_2-A$ est inversible puis déterminer les termes de $(I_2-A)^{-1}$.
-
Déterminer l'état stable $S$.
Partie B : Convergence de la suite $(U_n)$
-
Pour tout entier naturel $n$, on pose $V_n=U_n-S$.
Démontrer que pour tout entier naturel $n$, $V_{n+1}=AV_n$. -
En déduire que pour tout entier naturel $n$ : $V_n=A^n V_0$.
-
En déduire que pour tout entier naturel $n$ : $U_n=A^n(U_0-S)+S$.
-
Soit la matrice $P=\begin{pmatrix}3&1\\1&1\end{pmatrix}$.
Justifier que $P$ est inversible et déterminer $P^{-1}$. -
Soit $B=\begin{pmatrix}\dfrac{4}{5}&0\\ 0&\dfrac{3}{5}\end{pmatrix}$.
Démontrer que $P^{-1}AP=B$ -
Démontrer que pour tout entier naturel $n$, $A^n=PB^nP^{-1}$.
-
En déduire l'expression de $A^n$ en fonction de $n$.
-
En déduire que la suite $(U_n)$ converge vers une matrice colonne à déterminer.
-
Que déduire de cette limite en terme de population de lièvres arctiques et de lynx ?
Exercices
Matrices et opérations
Écrire la matrice d'ordre 2 telle que : $a_{11}=3$, $a_{22}=4$, $a_{12}=-1$ et $a_{21}=6$.
On considère deux matrices $A$ et $B$.
Déterminer les valeurs de $x$ telles que les matrices $A$ et $B$ soient égales.
$A=\begin{pmatrix} 1&x\\ 1-x&3 \end{pmatrix}$ et $B=\begin{pmatrix} 1&x^2\\ x^2+x+1&3-x \end{pmatrix}$
On considère les matrices : $A=\begin{pmatrix} 2&3&-5\\ 4&0&1\\ -1&1&3 \end{pmatrix}$ et $B=\begin{pmatrix} -2&2&1\\ 0&1&3\\ 2&-1&4 \end{pmatrix}$
Calculer $2A$, $-3B$, $A+B$, $3A-B$ et $-2A+4B$.
Soient les matrices $A=\begin{pmatrix} 2&-1 \\ 3&0\\ \end{pmatrix}$ et $B=\begin{pmatrix} 5&4\\ 1&8\\ \end{pmatrix}$
Calculer $(A+B)^2$ et $A^2+2AB+B^2$
On considère les matrices suivantes :
$A=\begin{pmatrix} 1&-1&1 \\ -3&2&-1\\ -2&1&0 \end{pmatrix}$ et $B=\begin{pmatrix} 2&4&6\\ 1&2&3 \end{pmatrix}$
Calculer $AB$, $BA$ et $A^2$
Calculer :
- $P_1=\begin{pmatrix} 2&3&-1\\ 4&0&2\\ -3&2&0 \end{pmatrix}\times \begin{pmatrix} 0&1&2\\ -2&2&3\\ 4&-2&1 \end{pmatrix}$
- $P_2=\begin{pmatrix} 5&-2&1&0\\ -1&3&2&1\\ 4&1&3&2\\ 0&-1&-1&1 \end{pmatrix}\times \begin{pmatrix} 2&0&3&1\\ 4&2&-1&-2\\ 2&1&0&3\\ -2&-1&2&1 \end{pmatrix}$
$A=\begin{pmatrix} 4&2\\ 2&1 \end{pmatrix}$
Montrer $A^2=5A$. Calculer rapidement $A^3$ et $A^4$.
Inverse de matrice
On considère la matrice $A=\begin{pmatrix} 0&0&1 \\ 0&1&0\\ 1&0&0 \end{pmatrix}$
Calculer $A^2$. En déduire que la matrice $A$ est inversible.
On considère la matrice $A=\begin{pmatrix} -3&1&1 \\ 1&-3&1\\ 1&1&-3 \end{pmatrix}$
-
Calculer $A^2+5A$.
-
En déduire que la matrice $A$ est inversible. Préciser son inverse $A^{-1}$.
Résolution de système
On considère le système suivant :$\left \{ \begin{array}{l} 2x+5y=13 \\ -3x-8y=11\\ \end{array} \right.$
-
Déterminer les matrices A et B telles que le système s'écrit sous forme matricielle $AX=B$ où $X=\begin{pmatrix} x \\ y\end{pmatrix}$.
-
Résoudre le système.
Soit $(S):\left \{\begin{array}{c} 2x_1+4x_2-x_3=1 \\ 3x_1-2x_2+x_3=2 \\ x_1-3x_2+x_3=4 \\ \end{array} \right.$
-
Écrire $(S)$ sous forme matricielle $AX=Y$.
-
Déterminer $A^{-1}$ à l'aide de la calculatrice.
-
En déduire les solutions de ce système.
-
Vérifiez que les matrices $A=\begin{pmatrix}1&-2&-2\\2&-3&-2\\-2&4&3\end{pmatrix}$ et $B=\begin{pmatrix}1&2&2\\2&1&2\\-2&0&-1\end{pmatrix}$ sont inverses l'une de l'autre.
-
En déduire une écriture matricielle et une solution des systèmes suivants :
- $\left \{\begin{array}{l} x-2y-2z=4 \\ 2x-3y-2z=5 \\ -2x+4y+3z=-3 \\ \end{array} \right.$
- $\left \{\begin{array}{l}x+2y+2z=-7 \\ 2x+y+2z=12 \\ -2x-z=9 \\ \end{array} \right.$
Puissances n-ième de matrice
Soient les matrices $A=\begin{pmatrix} 5&-4 \\ 4&-3 \end{pmatrix}$ et $J=\begin{pmatrix} 1&-1 \\ 1&-1 \end{pmatrix}$
-
Calculer $J^2$.
-
Démontrer que $A=I_2+4J$.
-
Démontrer que pour tout entier $n\geq 0$: $A^n=I_2+4nJ$.
On considère les matrices $A=\begin{pmatrix} 6&-1 \\ 2&3 \end{pmatrix}$ et $P=\begin{pmatrix} 1&1 \\ 1&2 \end{pmatrix}$
-
Justifier qu $P$ est une matrice inversible puis calculer $P^{-1}$.
-
Calculer $B=P^{-1}AP$.
-
Démontrer que pour tout entier naturel $n$ : $A^n=PB^nP^{-1}$.
-
En déduire l'expression de chaque terme de $A^n$ en fonction de l'entier naturel $n$.
Applications aux graphes
On considère le graphe non orienté suivant :
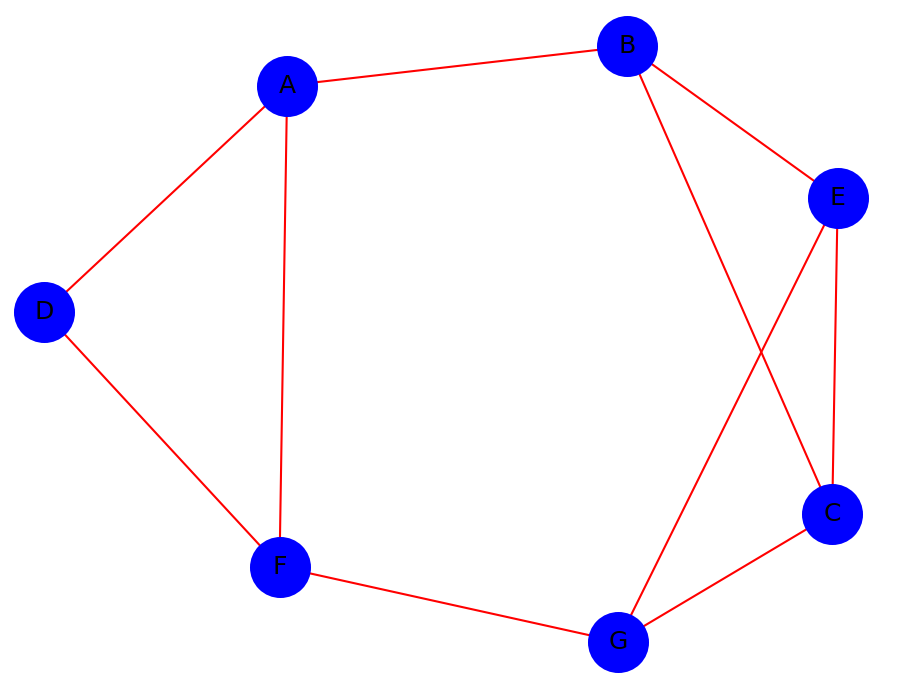
-
Déterminer une matrice d'adjacence $M$ de ce graphe.
-
Combien y-a-t-il de chaînes de longueur 10 reliant E à F?
On considère le graphe orienté suivant :
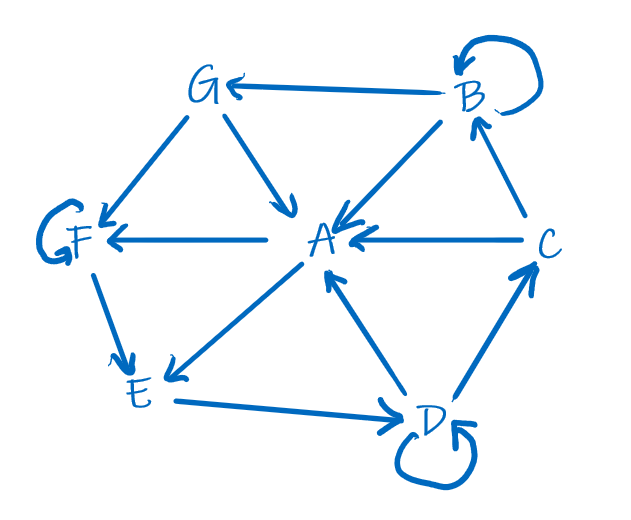
-
Déterminer une matrice d'adjacence $M$ de ce graphe.
-
Combien y-a-t-il de chemins de longueur 6 reliant D à B ?
Synthèses
Pour le cross des élèves de premières, un lycée a commandé 120 petites bouteilles d'eau et 180 sachets de biscuits pour la somme de 219,60 euros.
Pour le cross des élèves de terminale, l'établissement a commandé 100 bouteilles d'eau et 190 paquets de biscuits pour un total de 227,80 euros.
-
Modéliser cette situation sous forme d'un système $(S)$ de deux équations à deux inconnues $x$ et$y$ respectivement au prix d'une bouteille d'eau et à celui d'un paquet de biscuits.
-
Déterminer les matrices $A$, $X$ et $B$ telles que le système $(S)$ s'écrit sous la forme $AX=B$.
-
Résoudre le système. Interpréter la solution.
On considère les matrices $A= \frac12\begin{pmatrix} 0&1&1 \\ 1&0&1\\ 1&1&0 \end{pmatrix}$ et $P= \begin{pmatrix} 1&-1&-1 \\ 1&1&0\\ 1&0&1 \end{pmatrix}$.
-
En résolvant le système $PX=Y$ avec $X= \begin{pmatrix} x \\ y\\ z \end{pmatrix}$ et $Y= \begin{pmatrix} a \\ b\\ c \end{pmatrix}$.
Montrer que $P$ est inversible et donner son inverse.
- Calculer $P^{-1}AP$.
- Déterminer $A^n$ pour tout entier naturel $n$.
-
On considère les trois suites $(u_n)$, $(v_n)$ et $(w_n)$ définies par récurrence, pour $u_0$, $v_0$ et $w_0$ des réels , par :
$ \left \{ \begin{array}{c c} u_{n+1} & =\frac{v_n+w_n}{2} \\ v_{n+1} &=\frac{u_n+w_n}{2}\\w_{n+1}&=\frac{u_n+v_n}{2} \\ \end{array} \right. ,n\in\mathbb{N}$. On pose $U_n=\begin{pmatrix}u_n\\v_n\\w_n\end{pmatrix}$, pour tout $n\in\mathbb{N}$.
-
Déterminer une relation matricielle entre $U_{n+1}$ et $U_{n}$ pour tout entier $n$.
-
En déduire les limites des trois suites.
-
Le but de cet exercice est d'étudier, sur un exemple, une méthode de chiffrement publiée en 1929
par le mathématicien et cryptologue Lester Hill.
Ce chiffrement repose sur la donnée d'une matrice $A$, connue uniquement de l'émetteur et du destinataire.
Dans les parties 1 et 3 de cet exercice, cette matrice de cryptage est notée $A$ et est définie par :
$A = \begin{pmatrix}11&8\\6&5\end{pmatrix}$.
Attention ! La dernière partie est indépendante et nécessitera que vous mettiez en commun vos réflexions et calculs.
Partie A : cryptage
Voici les différentes étapes de chiffrement pour un mot comportant un nombre pair de lettres :
-
On divise le mot en blocs de deux lettres consécutives puis, pour chaque bloc, on effectue chacune des étapes suivantes.
-
On associe aux deux lettres du bloc les deux entiers $x_1$ et $x_2$ tous deux compris entre 0 et 25, qui correspondent aux deux lettres dans le même ordre, dans le tableau suivant :
A
B
C
D
E
F
G
H
I
J
K
L
M
0
1
2
3
4
5
6
7
8
9
10
11
12
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
13
14
15
16
17
18
19
20
21
22
23
24
25
-
On transforme la matrice $X = \begin{pmatrix}x_1\\x_2\end{pmatrix}$ en la matrice $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ vérifiant $Y = A X$.
-
On transforme la matrice $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ en la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$, où $r_1$ est le reste de la division euclidienne de $y_1$ par 26 et $r_2$ celui de la division euclidienne de $y_2$ par 26.
-
On associe aux entiers $r_1$ et $r_2$ les deux lettres correspondantes du tableau de l'étape 2.
Le bloc chiffré est le bloc obtenu en juxtaposant ces deux lettres.
-
utiliser la méthode de chiffrement exposée pour chiffrer le mot HILL.
Partie B : un programme informatique utile pour une étape du décryptage
On considère la fonction suivante écrite en langage naturel :
fonction(a un nombre entier naturel) :
n prend la valeur 0
r prend la valeur 0
Tant que r≠1 et n<26 :
n est incrémenté de 1
r prend la valeur du reste de la division euclidienne de n×a par 26
Fin Tant que
renvoyer n
-
-
La fonction prend comme argument la valeur $a = 7$.
Reproduire et compléter le tableau suivant jusqu'à l'arrêt de l'algorithme. Vous devez saisir dans ce tableau les valeurs successivement prises par les variables
netrau cours de l'exécution de l'algorithme.n
0
1
2
...
r
0
...
...
...
-
En déduire l'existence d'un nombre entier naturel $k$ tel que $7\times k \equiv 1\ [26]$.
-
Écrire la fonction précédente en langage Python puis vérifier le résultat obtenu précédemment.
-
Que renvoie la fonction précédente codée en Python lorsque son argument est 8 ?
Expliquer la signification de la valeur obtenue. -
Écrire une fonction
liste_resultatsqui ne prend pas de paramètre d'entrée et qui renvoie la liste des 26 résultats retourné par la fonction précédente ; le terme d'index $i$ correspond donc au renvoi de la fonction précédente lorsqu'en entrée son argument est $i$. -
Conjecturer une condition nécessaire et suffisante portant sur un entier naturel $i$ compris entre 0 et 25 pour que le renvoi de la fonction précédente ne soit pas 26.
-
Partie C : décryptage d'un message codé
-
-
Justifier que la matrice $A$ la matrice définie par : $\begin{pmatrix}11&8\\6&5\end{pmatrix}$ admet une matrice inverse dans $\mathcal{M}_{np}(\mathbb{R})$, matrice à déterminer.
-
Pour pouvoir décrypter des messages codés à partir de la matrice $A$, il faut obtenir une matrice $B$ a coefficients entiers telle que $AB=BA=\begin{pmatrix}i_{11}&i_{12}\\i_{21}&i_{22}\end{pmatrix}$ où $i_{11}\equiv 1\ [26]$, $i_{12}\equiv 0\ [26]$, $i_{21}\equiv 0\ [26]$ et $i_{22}\equiv 1\ [26]$.
Pourquoi la matrice obtenue à la question précédente ne convient pas ?
-
-
On rappelle que $A$ est la matrice $A = \begin{pmatrix}11&8\\6&5\end{pmatrix}$ et on note $I$ la matrice : $I = \begin{pmatrix}1&0\\0&1\end{pmatrix}$.
-
Calculer la matrice $16A-A^2$.
-
En déduire la matrice $B$ telle que $BA = 7I$.
-
Démontrer que si $A X = Y$, alors $7 X = B Y$
-
-
On veut déchiffrer le mot XUSL.
On note $X = \begin{pmatrix}x_1\\x_2\end{pmatrix}$ la matrice associée, selon le tableau de correspondance, à un bloc de deux lettres avant chiffrement, et $Y = \begin{pmatrix}y_1\\y_2\end{pmatrix}$ la matrice définie par l'égalité : $Y = A X = \begin{pmatrix}11&8\\6&5\end{pmatrix}X$.
Si $r_1$ et $r_2$ sont les restes respectifs de $y_1$ et $y_2$ dans la division euclidienne par 26, le bloc de deux lettres après chiffrement est associé à la matrice $R = \begin{pmatrix}r_1\\r_2\end{pmatrix}$.
-
Démontrer que : $\left\{\begin{array}{l c l} 7x_1 &=& \phantom{-}5y_1 - 8y_2\\ 7x_2 &=&- 6y_1 + 11 y_2 \end{array}\right.$.
-
En utilisant des questions précédentes, établir que : $\left\{\begin{array}{l c l r} x_1 &\equiv&23r_1 + 10r_2 \:\:&[26]\\ x_2 &\equiv&14r_1 + 9r_2 \:\:&[26] \end{array}\right.$.
-
Décrypter le mot XUSL, associé aux matrices $\begin{pmatrix}23\\20\end{pmatrix}$ et $\begin{pmatrix}18\\11\end{pmatrix}$.
-
Partie D : nouvelle mission secrète pour vous
Les services secrets français de contre-espionnage pour qui vous travaillez en secret viennent de vous confier une nouvelle mission : décrypter le message envoyé par le groupe que vous surveillez. Voici le message crypté reçu :
île : indice qu'à Troie.
VZVGOUFIQLRYMWITISUT

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International