Demander le programme !

Contenu :

Capacités attendues

Démonstrations

Chaîne de Markov

Exemple introductif

Lors d'un travail de recherche, un étudiant lit différentes pages internet. Ils passent d'une page à l'autre à partir des liens hypertexte.
Cet étudiant juge la page soit pertinente, soit non pertinente.
L'expérience acquise au cours de ce type de recherche permet de prévoir que si :

On note $V_n$ l'événement "la $n$-ième page est pertinente".
On suppose que la première page est pertinente.

  1. Modéliser le parcours sur les trois premières pages de la recherche par un arbre de probabilité en utilisant la notation $V_n$.

  2. Compléter cet arbre pour illustrer le parcours sur les $n$ premières pages.

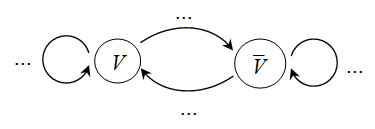
  3. Plutôt que d'utiliser un tel arbre, on peut modéliser la situation par un graphe probabiliste comme celui-ci dessous où $V$ correspond à l'événement "la page est pertinente" et où toute flèche correspond au passage à une page suivante.
    Le reproduire et le compléter.

Code de déblocage de la correction :

Vocabulaire sur les graphes

Un graphe orienté est pondéré lorsque chaque arête est affectée d'un nombre réel positif appelé poids de cette arête.

Un graphe probabiliste est un graphe orienté où tous les poids sont des réels compris entre 0 et 1 et tel que la somme des poids des arêtes issues d'un même sommet est 1.

  1. Déterminer les valeurs de $x$ et de $y$ pour que le graphe ci-dessous soit un graphe probabiliste.

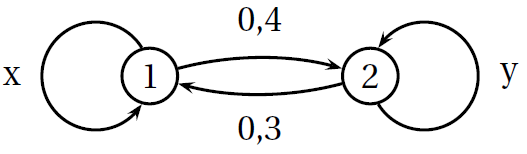
  2. Est-ce un graphe probabiliste ? Pourquoi ?

Code de déblocage de la correction :

matrice associée

La matrice associée à un graphe probabiliste comportant $k$ sommets d'appelle une matrice de transition.

Cette matrice de transition est une matrice carrée d'ordre $k$ où le terme de la $i$-ième ligne et de la $j$-ième colonne est égale au poids de l'arête allant du sommet $i$ au sommet $j$ si elle existe, 0 sinon.

On reprend l'exemple introductif. On avez vu que le problème concret peut être modéliser par le graphe probabiliste suivant :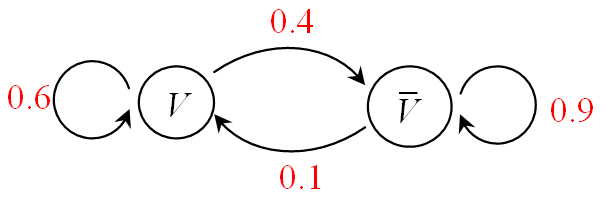

  1. En considérant comme ordre de sommet "$V$ puis $\overline{V}$", donner la matrice de transition associée à ce graphe probabiliste.

  2. Que remarquez-vous sur les coefficients d'une même ligne de cette matrice de transition ?

Code de déblocage de la correction :

La somme des termes appartenant à la même ligne d'une matrice de transition vaut toujours 1.

  1. Recopier et compléter la matrice de transition $T$ ci-dessous.
    $T=\begin{pmatrix} ...&0.6&0.1 \\ 1&...&...\\ ...&0.3&0.5 \end{pmatrix}$

  2. En notant les sommets dans cet ordre $A$, $B$, $C$, proposer un graphe probabiliste qui correspond à cette matrice de transition.

Code de déblocage de la correction :

Chaîne de Markov

Revenons à l'exemple introductif. On considère la suite de la pertinence des pages visitées.
Pour chaque page, il n'y a que deux possibilités :

Voici des exemples possibles de telle suite, sachant que l'on a supposé que la première page est forcément pertinente :

Nous avons supposé que la probabilité qu'une page soit pertinente ne dépend que de la pertinence ou non de la page précédente.
On peut voir cela d'une autre manière : lorsque l'on est sur une page, la pertinence de la page future ne dépend pas des pages passées, mais seulement de celle actuelle.

Nous avons aussi supposé que les probabilités pour passer d'un état de pertinence à un autre sont indépendantes du nombre de pages déjà visitées.

Une chaîne de Markov est une suite $(X_n)$ de variables aléatoires modélisant l'évolution par étapes successives d'un système aléatoire comportant différents états telle que :

À l'étape $n=0$, la probabilité de $X_0$ s'appelle la distribution initiale du système, souvent notée $\pi_0$.
Dans le cas de $k$ états différents, $\pi_0 = (P(X_0)=E_1\ P(X_0)=E_2\ ...\ P(X_0)=E_k)$.

À l'étape $n$, la probabilité de $X_n$ s'appelle la distribution après $n$ transitions, , souvent notée $\pi_n$.
Dans le cas de $k$ états différents, $\pi_n = (P(X_n)=E_1\ P(X_n)=E_2\ ...\ P(X_n)=E_k)$.

On peut associer à toute chaîne de Markov :

On considère un pays subissant une épidémie ; ses habitants peuvent être dans trois états :

Des études montrent que, d'un mois à l'autre, chaque habitant peut voir son état changer selon les règles suivantes :

Au début de l'épidémie, 2% de la population est malade et 1% est immunisée.

  1. Quel est l'ensemble des états possibles ?

  2. Justifier que l'évolution de l'état d'un individu mois par mois peut être modélisé par une chaîne de Markov.

  3. Proposer le graphe probabiliste associé à cette chaîne de Markov.

  4. Proposer la matrice de transition $T$ associée (en conservant l'ordre alphabétique).

  5. Déterminer la distribution initiale $P_0$ du système.

  6. Que représente concrètement les coefficients obtenus par le calcul $ P_0 T$ ?

Code de déblocage de la correction :

Évolution d'une chaîne de Markov

On considère dans cette partie une chaine de Markov $(X_n)$ dont la matrice de transition est notée $T$.
On note $P_n$ la distribution après $n$ transitions écrite sous forme d'une matrice ligne ayant autant de colonne que d'états différents et telle que le terme de la $j$-ième colonne est la probabilité qu'à l'étape $n$ la variable $X_n$ soit égale à l'état $E_j$.
Ainsi, pour tout entier naturel non nul $n$, on note : $P_n=\begin{pmatrix} P(X_n=E_1)&...&P(X_n=E_j)&...&P(X_n=E_k) \end{pmatrix}$ si $k$ est le nombre d'états.

Pour tout entier naturel non nul $n$, $P_{n+1}=P_n\times T$.

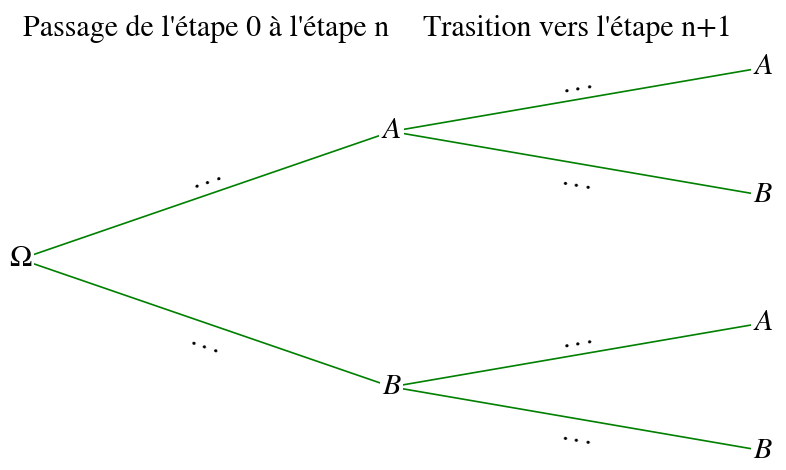
On considère ici une chaîne de Markov à deux états $A$ et $B$ dont voici le graphe associée : 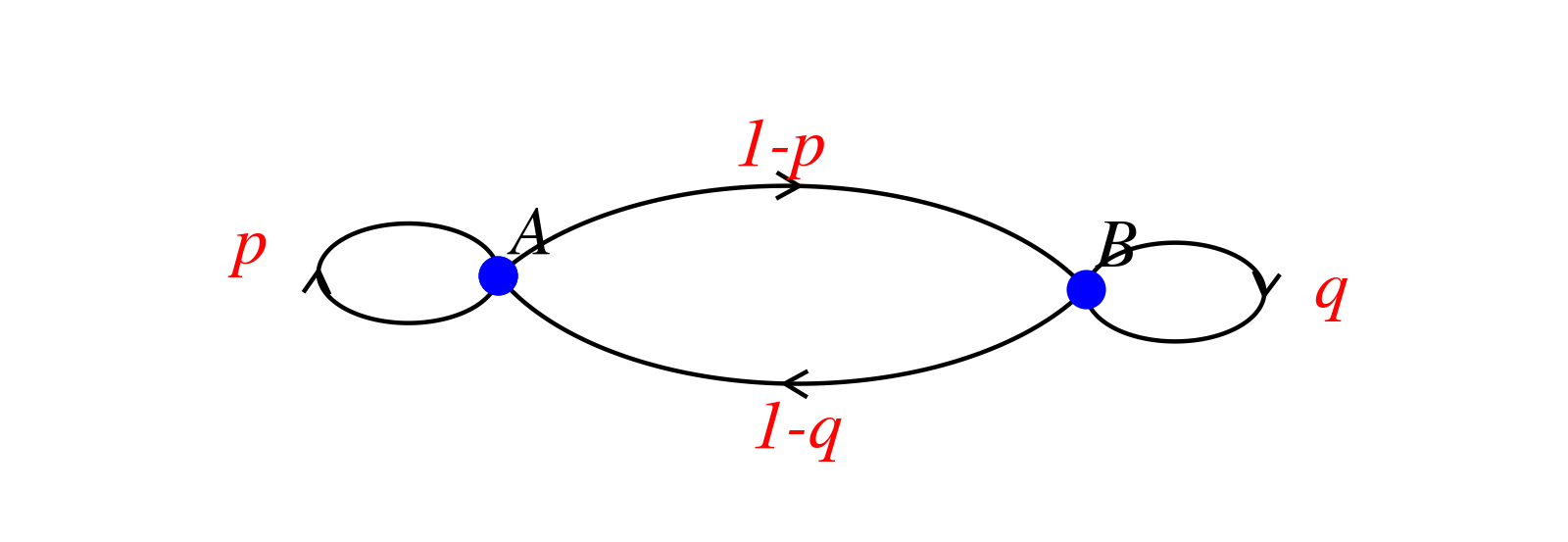On considère ici que $0\le p \le1$ et $0\le q \le 1$.
La matrice associée est donc : $T=\begin{pmatrix} p&1-p \\1-q&q \end{pmatrix}$

On note $P_n=\begin{pmatrix} P(X_n=A)&P(X_n=B) \end{pmatrix}$ la distribution après $n$ transitions et $P_{n+1}=\begin{pmatrix} P(X_{n+1}=A)&P(X_{n+1}=B) \end{pmatrix}$ la distribution après $n+1$ transitions.

  1. Développer le produit matriciel $P_n\times T$.

  2. Compléter l'arbre de probabilité suivant :

  3. En déduire l'expression de $P_{n+1}$ en fonction de $P(X_n=A)$ et de $P(X_n=B)$.

  4. Conclure.

Code de déblocage de la correction :

Pour tout état $E_i$ et $E_j$ et pour tout entier naturel $n\ge 1$, le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^n$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $n$ transitions.

On considère ici une chaîne de Markov à deux états $A$ et $B$ dont voici le graphe associée : On considère ici que $0\le p \le1$ et $0\le q \le 1$.
La matrice associée est donc : $T=\begin{pmatrix} p&1-p \\1-q&q \end{pmatrix}$

On note $P_n=\begin{pmatrix} P(X_n=A)&P(X_n=B) \end{pmatrix}$ la distribution après $n$ transitions et $P_{n+1}=\begin{pmatrix} P(X_{n+1}=A)&P(X_{n+1}=B) \end{pmatrix}$ la distribution après $n+1$ transitions.

Voici une démonstration de ce théorème avec quelques éléments à préciser.
Commencer par lire la démonstration ci-dessous avant de répondre aux questions qui suivent :

Montrons par récurrence que la propriété "le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^n$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $n$ transitions" est vraie pour tout entier naturel $n$ non nul.

Initialisation : pour $n=1$ :
Par définition de la matrice $T$, le coefficient $T_{ij}$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en une transition : $T_{ij}=P_{(X_0=E_i)}(X_{1}=E_j)$.
La propriété est donc vraie au rang initial.

Hérédité : considérons un entier $k\ge 1$ tel que "le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^k$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $k$ transitions".
Montrons que "le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^{k+1}$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $k+1$ transitions".
Soient $E_i$ et $E_j$ deux des états possibles ($A$ ou $B$ ici).
Par hypothèse de récurrence : $T^k = \begin{pmatrix} P_{(X_0=A)}(X_{k}=A) &P_{(X_0=A)}(X_{k}=B) \\ P_{(X_0=B)}(X_{k}=A)& P_{(X_0=B)}(X_{k}=B)\end{pmatrix}$ puisque le coefficient $T^k_{ij}$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $k$ transitions : $T^k_{ij}=P_{(X_0=E_i)}(X_{k}=E_j)$.

On va calculer la probabilité de passer de l'état $E_i$ à celui $E_j$ en $k+1$ transitions.
Affirmation 1 :
$P_{(X_0=E_i)}(X_{k+1}=E_j)=P_{(X_0=E_i)}((X_{k+1}=E_j)\cap (X_{k}=A))+P_{(X_0=E_i)}((X_{k+1}=E_j)\cap (X_{k}=B))$ $=P_{(X_0=E_i)}(X_{k}=A)\times P_{(X_k=A)}(X_{k+1}=E_j)+P_{(X_0=E_i)}(X_{k}=B)\times P_{(X_k=B)}(X_{k+1}=E_j)$

Ainsi : Affirmation 2 :
$P_{(X_0=E_i)}(X_{k+1}=E_j)=P_{(X_0=E_i)}(X_{k}=A)\times T_{1j}+P_{(X_0=E_i)}(X_{k}=B)\times T_{2j}$.

Or, $T^{k+1}=T^k\times T$, ainsi :
Affirmation 3 : $T^{k+1}_{ij}=P_{(X_0=E_i)}(X_{k}=A)\times T_{1j}+P_{(X_0=E_i)}(X_{k}=B)\times T_{2j}$.
Dès lors, $T^{k+1}_{ij}=P_{(X_0=E_i)}(X_{k+1}=E_j)$.
En notant $A$ et $B$, les deux états possibles, on a bien : $T^{k+1} = \begin{pmatrix} P_{(X_0=A)}(X_{k+1}=A) &P_{(X_0=A)}(X_{k+1}=B) \\ P_{(X_0=B)}(X_{k+1}=A)& P_{(X_0=B)}(X_{k+1}=B)\end{pmatrix}$.
Ainsi, on a démontré que le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^{k+1}$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $k+1$ transitions".
La propriété est donc héréditaire.

Conclusion : pour tout entier naturel $n\ge 1$, le coefficient de la ligne $i$ et de la colonne $j$ de la matrice $T^n$ est la probabilité de passer de l'état $E_i$ à celui $E_j$ en $n$ transitions.

  1. Justifier l'affirmation 1.

  2. Quel élément de la définition d'une chaîne de Markov permet de justifier l'affirmation 2 ?

  3. Exprimer les coefficients de la matrice $T^k \times T$ en focntion des coefficients de la matrice $T$ et de ceux de $T^k$ pour justifier l'affirmation 3.

Code de déblocage de la correction :

Pour tout entier naturel $n$ non nul, $P_n=P_0 T^n$.

Démontrer ce résultat dans le cas de deux états $A$ et $B$.

Code de déblocage de la correction :

Un internaute navigue sur un mini Web composé de trois pages. Ces pages possèdent des liens hypertextes qui permettent de passer de certaines à d'autres par simple clic.
Voici la structure obtenue avec ces liens :

  1. Représenter la situation par un graphe probabiliste.

  2. Déterminer la matrice de transition $T$ associée à ce graphe probabiliste.

  3. On admet que $T^2=\begin{pmatrix} \frac{1}{2}&\frac{1}{3}&\frac{1}{6}\\ \frac{1}{4}&\frac{25}{48}&\frac{11}{48} \\ \frac{1}{4}&\frac{11}{24}&\frac{7}{24}\end{pmatrix}$.

    Quelle est la signification concrète de $T^2_{23}=\frac{11}{48}$ ?

  4. L'internaute est sur la page A et effectue 10 clics.
    Sur quelle page a-t-il le plus de chance d'arriver ? Justifier.

Code de déblocage de la correction :

Étude asymptotique

Soit $(X_n)$ une chaîne de Markov à 2 ou 3 états de matrice de transition $T$.
S'il existe un entier naturel $n$ tel que la matrice $T^n$ ne contient pas de 0 alors la suite $(P_n)$ converge vers l'unique matrice $\pi$ vérifiant $\pi T=\pi$ et telle que tous ses coefficients sont compris entre 0 et 1 et telle que leur somme donne 1.
De plus, cette limite $\pi$ ne dépend pas de la distribution initiale $P_0$.

Dire que la matrice $T^n$ ne contient pas de 0 signifie que l'on peut passer de n'importe quel état à n'importe quel autre en exactement $n$ étapes.

En particulier pour $n=1$, si la matrice de transition $T$ ne contient pas de 0 alors la suite $(P_n)$ converge vers une telle matrice $\pi$ vérifiant $\pi T=\pi$.

En cas d'existence, une telle distribution $\pi$ est appelée la distribution invariante de la chaîne de Markov.

On reprend l'exercice sur le surf dans un mini Web avec la notation $T$ pour sa matrice de transition.

  1. Soit $P$ la matrice définie par $P=\begin{pmatrix} \frac{1}{3}&\frac{4}{9}&\frac{2}{9}\end{pmatrix}$.
    Calculer le produit matriciel $P T$.

  2. Que pouvez-vous en déduire ?

  3. On considère un internaute qui navigue sur ce mini Web. Il part d'une page quelconque.
    Sur quelle page a-t-il le plus de chance de se touver à très long terme ?
    Sur quelle page a-t-il le moins de chance de se touver à très long terme ?

Code de déblocage de la correction :

L'algorithme de PageRank® qui a fait la fortune du groupe Google est une amélioration de la démarche vue dans cet exercice.

Un ordinateur a été programmé pour afficher une succession de lettres. Ces lettres sont soient des consonnes (C), soit des voyelles (V).
On admet que le programme conduit à cette règle constante :

  1. Représenter la situation par un graphe probabiliste.

  2. Déterminer la matrice de transition associée à ce graphe probabiliste.

  3. On suppose que la première lettre est une voyelle.
    Déterminer la probabilité que la dixième lettre soit une consonne.

  4. On pose $\pi=\begin{pmatrix} x&y \end{pmatrix}$.
    Justifier que $\pi$ est la distribution invariante du système si, et seulement si, $(x;y)$ est solution du système : $\left \{ \begin{array}{rcl} 0.8x-0.5y&=&0 \\ x+y&=&1 \end{array} \right.$

  5. En déduire la distribution invariante de ce système.

  6. Interpréter le résultat.

Code de déblocage de la correction :

Exercices

Détreminer dans chacun des cas si la suite $(X_n)$ est une chaîne de Markov.
On dispose de deux urnes A et B contenant au départ dix boules numérotées de 1 à 10.
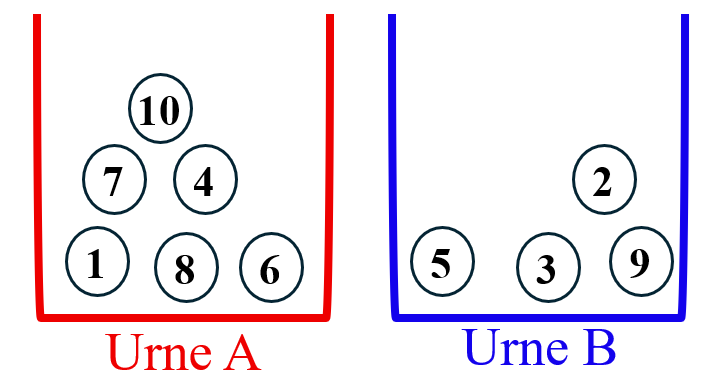
$(X_n)$ désigne le nombre de boules dans A après l'étape $n$.

  1. À chaque étape, on tire un numéro au hasard entre 1 et 10 et on change d'urne la boule choisie.

  2. À chaque étape, on tire un numéro au hasard entre 1 et 10 et on change d'urne la boule choisie si son numéro est plus grand que la boule précédemment tirée.

  3. À chaque étape, on tire un numéro au hasard entre 1 et 10 et on change d'urne la boule choisie si son numéro est plus grand parmi toutes les boules de l'urne A.

  4. À chaque étape, on tire un numéro au hasard entre 1 et 10 et on change d'urne la boule choisie si son numéro est pair.

On étudie l'effet de la présence d'un requin bleu dans une zone dans laquelle ses proies possibles sont des calmars ($C$), des poissions ($P$) et des petits prequins ($R$).
Le choix de la proie ne dépend que de celle choisie précédemment.
On modélise la situation par une chaîne de Markov dont le grape pondéré est donné ci-dessous.

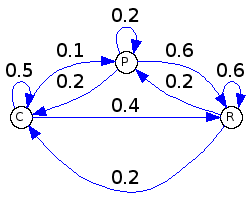
Au début de l'étude, le requin bleu a choisi un calmar comme proie.

  1. Compléter la fonction distribution ci-dessous qui renvoie après n proies dévorées la distribution $\pi_n$ lorsque la distribution initiale est (c p r). 

    def distribution(c, p, r, n):
    for i in range(n):
        _c = c 
        _p = p 
        _r = r 
        c = 0.5*_c + 0.2*_p + 0.2*_r 
        ...
        ...
    return (c, p, r)

  2. Utiliser la fonction distribution pour conjecturer une distribution invariante $\pi$.

  3. Déterminer la matrice de transition $T$ associée au modèle.

  4. Vérifier que la distribution $\pi$ conjecturée est bien une distribution invariante et que c'est la seule existante et qu'elle est indépendante de la proie initialement dévorée.

Le modèle des urnes d'Ehrenfest fut développé en 1907 par Paul et Tatiana Ehrenfest afin de lever le "paradoxe" de l'irréversibilité dans la dynamique des particules.
En effet, à notre échelle, la plupart des phénomènes macroscopiques sont irréversibles, alors que les lois de la dynamique des particules sont réversibles.
Le modèle des urnes d'Ehrenfest cherche à montrer qu'un système comportant un grand nombre de particules aux évolutions réversibles a une évolution macroscopique irréversible.

On le modélise avec deux urnes $U_1$ et $U_2$ et $k$ billes respectant un processus d'échange :

Partie A : cas où $k=2$

On note $X_n$ le contenu de l'urne $U_1$ après $n$ étapes et on note $\pi_n$ la matrice ligne donnant la distibution de $X_n$.

  1. Donner les distributions $\pi_0$ et $\pi_1$.

  2. Représenter la chaîne de Markov des variables aléatoires $(X_n)$ à l'aide d'un graphe probabiliste à 3 états à définir.

  3. Donner la matrice de transition $T$ associée à ce graphe probabiliste.

  4. Montrer par récurrence que pour tout entier $m\ge 0$ : $\pi_{2m+1}=(0\ \ 1\ \ 0)$ et $\pi_{2m}=\left(\dfrac{1}{2}\ \ 0\ \ \dfrac{1}{2}\right)$

  5. La suite $(\pi_n)$ est-elle convergente vers une distibution invariante ?

Partie B : cas général simulé

On suppose désormais qu'il y a $k$ billes, avec $k>2$.
On note $S_m$ la variable aléatoire donnant le nombre de billes présentes dans l'urne $U_1$ après $m$ échanges.

La fonction Ehrenfest ci-dessous doit simuler le contenu de l'urne $U_1$ dans le cas où il a $k$ billes dans le système et n échanges et doit renvoyer la liste S correspondant aux différentes valeurs prises par $S_m$ pour les étapes 0 à $n$. 

import random
import matplotlib.pyplot as plt

def Ehrenfest(k, n):
    """
    k est un entier correspond au nombre de billes dnas l'ensemble des deux urnes 
    n est le nombre d'échanges en tout.
    """
    U1 = [i for i in range(1, k+1)]   # ligne 9
    S = ...    # liste contenant la succession des nombres de billes dans l'urne U1
    for j in range(n):
        num_bille = random.randint(1, k)
        if num_bille in U1:
            U1.remove(num_bille) # suppression de num_bille de l'urne U1
        else:
            ...
        S.append(...)
    return S

  1. Quel est rôle de la ligne 9 du script ci-dessus ? 

        U1 = [i for i in range(1, k+1)]   # ligne 9

  2. Compléter la fonction Ehrenfest au niveau des pointillés.

  3. Tester la fonction en exécutant print(Ehrenfest(500, 1000)).
    En regardant les dernières valeurs de la liste affichée, que pouvez-vous conjecturer sur la répartition des $k$ billes au bout d'un grand nombre d'échange ?

  4. Rajouter les lignes suivantes à la suite du script précédent : 

    # pour le tracé d'une courbe représentant Sn en fonction de n
x = [i for i in range(10001)]
y = Ehrenfest(500, 10000)
plt.clf()           # pour effacer tout tracé précédent
plt.xlim(0,10000)   # pour fixer l'affichage en abscisses entre 0 et 10000
plt.ylim(0,500)     # pour fixer l'affichage en ordonnées entre 0 et 500
plt.gca().yaxis.set_ticks(range(0, 501, 50))  # pour imposer une graduation de 50 en 50 en ordonnées
plt.gca().yaxis.grid(True, which = 'both', color = 'gray', zorder = 0) # pour dessiner les lignes liées aux graduations en ordonnées
plt.plot(x,y)
plt.show()

    Exécuter le script complet pour visualiser l'évolution du nombre de billes dans l'urne $U_1$ sur un grand nombre d'échanges.

  5. Modifier le script afin d'étudier l'évolution de l'urne pour différentes valeurs de $k$ et de $n$.

  6. Comment semble se comporter la suite $(S_n)$ lorsque $n$ tend vers $+\infty$ ?

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲