TP3 : Dérivation et variation
Dans ce tp , nous allons manipuler l'outils "dérivation".
L'opérateur de dérivée opère sur les fonctions. La dérivée d'une fonction $f$ sera noté $f'(x)$.
C'est Xcas qui va nous permettre ou ed faire les calculs de dérivées.
Dériver
On rappelle les formules de dérivation suivantes :
- La dérivée d'un nombre est 0. Exemples : $(5)'=0$, $(-356)'=0$
- $(x^n)'=nx^{n-1}$. Exemple : $(x^3)'=3x^{3-1}=3x^2$
- La dérivée d'un nombre multiplié par une fonction est la nombre multiplié par la dérivée de la fonction. Exemples : $(3f(x))'=3f'(x)$, $(2x^3)'=2\times 3x^2=6x^2$.
- La dérivée d'une somme est la somme des dérivée. Exemples : $(x^2-3x)'=(x^2)'-3(x)'=2x-3$
Dériver les fonctions suivantes :
- $f_1(x)=2x^5$
- $f_2(x)=2x$
- $f_3(x)=-5$
- $f_4(x)=3x^3-4x^2$
- $f_5(x)=-5x^5+3x^2-6$
On rappelle les formules de dérivation suivantes :
- $(uv)'=u'v-uv'$. Exemples : $(x^2(2x-1))'=2x(2x-1)+x^2(2)=4x^2-2x+2x^2=6x^2-2x$
- $(\frac{u}{v})'=\frac{u'v-uv'}{v^2}$. Exemples : $(\frac{x^2}{2x-1})'=\frac{2x(2x-1)-x^2\times 2}{(2x-1)^2}=\frac{4x^2-2x-2x^2}{(2x-1)^2}=\frac{2x^2-2x}{(2x-1)^2}.$
Dériver les fonctions suivantes :
- $f_1(x)=(x-2)(3x+1)$
- $f_2(x)=(x^2-x)(3x-1)$
- $f_4(x)=\frac{x+1}{x-1}$
- $f_5(x)=\frac{x}{x^2+5}$
Dériver les fonctions suivantes :
- $f(x)=x^3-3x+2$
- $g(x)=\frac{2x+1}{x-5}$
- $h(x)=\frac{x+1}{(x-1)(5-x)}$
Avant de dériver, il faut évidement implémenter la fonction (cf TP2).
En xcas pour obtenir la dérivée, il suffit d'écrire :

Dériver pourquoi?
L'outils sert essentiellement à déterminer les variations d'une fonction grâce à ce théorème :
- $f$ est croissante sur $I$ si, et seulement $f'(x)\geq 0$ sur $I$.
- $f$ est strictement croissante sur $I$ si, et seulement $f'(x)> 0$ sur $I$.
- $f$ est décroissante sur $I$ si, et seulement $f'(x)\leq 0$ sur $I$.
- $f$ est strictement décroissante sur $I$ si, et seulement $f'(x)< 0$ sur $I$.
On réalisera ainsi des tableaux de variations :
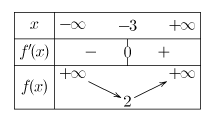
Réaliser les tableaux de variations des fonctions suivantes :
- $f(x)=x^3-3x+2$ pour $x\in\mathbb{R}$
- $g(x)=\frac{2x+1}{x-5}$ pour $x\in\mathbb{R}\backslash\{5\}$
- $h(x)=\frac{x+1}{(x-1)(5-x)}$ pour $x\in\mathbb{R}\backslash\{1;5\}$