Un pont à une seule arche d'une longueur de 16 mètres, enjambe une route à double circulation.

La figue ci-dessous donne une vue de l'une des deux façades de ce pont ( une unité représente 1 mètre).

La partie supérieure du pont est à une hauteur de 5 mètres au-dessus de la route.

La partie de l'axe des abscisses comprises entre -8 et 8 représente la chaussée sur laquelle sont délimitées les zones de circulation des piétons, des cyclistes et des véhicules motorisés.

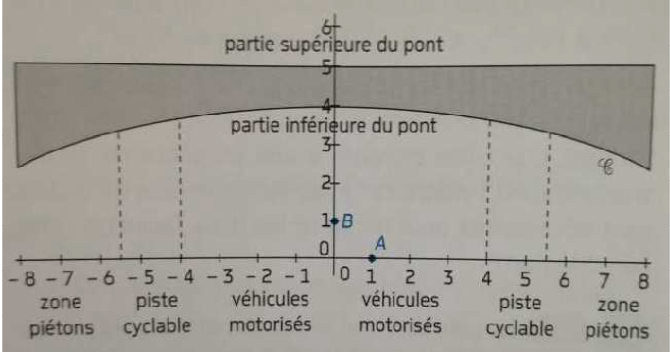
1. Étude de la fonction $f$ représentée par la courbe $\mathcal{C}$

   Soit la fonction $f$ définie, pour tout nombre réel $x$ de l'intervalle $[-8;8]$, par $f(x)=a-\frac{e^{0,2x}+e^{-0,2x}}{2}$, où $a$ désigne un nombre entier naturel.

   On note $\mathcal{C}$ sa courbe représentative donnée ci-dessus.

   1. Déterminer graphiquement $f(0)$. En déduire la valeur de $a$.
   2. Déterminer une expression de la dérivée de $f$, $f'(x)$.
   3. Calculer $f'(0)$. En déduire la valeur du coefficient directeur de la tangente $T$ à la courbe $\mathcal{C}$ en son point d'abscisse $0$.
   4. Résoudre algébriquement, pour tout nombre rée $x$ de l'intervalle $[-8;8]$, l'inéquation $f'(x)>0$.
   5. Dresser le tableau de variation de la fonction $f$ sur l'intervalle $[-8;8]$
   6. Déterminer la hauteur maximale d'un véhicule motorisé pour qu'il puisse passer sous ce pont en tenant compte du fait que l'on doit laisser une hauteur de sécurité de $50$ cm au dessus du véhicule.
2. Calcul d'aire

   On veut peindre les deux façades de l'armature du pont à arche.

   1. Calculer la surface d'une façade du pont.
   2. Montrer que la surface totales à peindre est environ de $47,51 m^2$.
   3. La peinture utilisée pour peindre les façades du pont est vendue par bidon de 30 litres. Sachant que cette peinture a une propriété recouvrement de $0,3 m^2/l$, combien de bidons sont nécessaires pour recouvrir les deux faces de cette construction?

Code de déblocage de la correction de l'exercice 1 :

On définit la fonction $f(x)=\frac{x+2}{3-x}$ pour $x\in]-\infty,3[\cup]3;+\infty[$.

1. Déterminer les limites de $f$ en $-\infty$, en $3^{-}$, en $3^{+}$ et en $+\infty$.($\lim\limits_{x\to +\infty}f(x)$)
2. Etablir le tableau de variation de $f$ sur $x\in]-\infty,3[\cup]3;+\infty[$.
3. Déterminer le signe de $f(x)$ sur $x\in]-\infty,3[\cup]3;+\infty[$
4. Déterminer l'équation de la tangente en 2 de $f$.
5. Déterminer l'aire de la surface délimitée par la courbe représentatif de $f$, l'axe des abscisses, et les droites d'équations $x=1$ et $x=2$ en u.a..
6. L'unité graphique est de 2 cm en abscisses et de 3 cm en ordonnée; Déterminer la surface précédente en $cm^2$.

On définit la fonction $f(x)=(2x+3)e^{-2x}$ pour $x\in\mathcal{R}$.

1. Déterminer les limites de $f$ en $-\infty$ et en $+\infty$. Qu'en déduire?
2. Etablir le tableau de variation de $f$ sur $x\in\mathcal{R}$.
3. Déterminer l'équation de la tangente en -1.
4. Déterminer le signe de $f(x)$ sur $x\in\mathcal{R}$
5. Déterminer l'aire de la surface délimitée par la courbe représentatif de $f$, l'axe des abscisses, et les droites d'équations $x=-1$ et $x=0$ en u.a..
6. On admet que $f(x)>x^3$ pour $x\in[-1;0]$. Déterminer l'aire de la surface délimitée par la courbe représentative de $f$, par la courbe d'équation $y=-x^3$ et par les droites d'éqautions $x=-1$ et $x=0$ en u.a.
7. L'unité graphique est de 2 cm en abscisses et de 3 cm en ordonnée; Déterminer la surface précédente en $cm^2$.

On définit la fonction $f(x)=(x)e^{3x-2}$ pour $x\in\mathcal{R}$.

1. Déterminer les limites de $f$ en $-\infty$ et en $+\infty$. Qu'en déduire?
2. Etablir le tableau de variation de $f$ sur $\mathcal{R}$.
3. Déterminer l'équation de la tangente en -1.
4. Déterminer le signe de $f(x)$ sur $\mathcal{R}$
5. Déterminer l'aire de la surface délimitée par la courbe représentatif de $f$, l'axe des abscisses, et les droites d'équations $x=0$ et $x=1$ en u.a..
6. On admet que $f(x)>x^2$ pour $x\in[0;1]$. Déterminer l'aire de la surface délimitée par la courbe représentative de $f$, par la courbe d'équation $y=x^2$ et par les droites d'éqautions $x=0$ et $x=1$ en u.a.
7. L'unité graphique est de 5 cm en abscisses et de 2 cm en ordonnée; Déterminer la surface précédente en $cm^2$.

On définit la fonction $f(x)=(x+1)ln(x+1)$ pour $x\in]-1;+\infty[$.

1. Déterminer les limites de $f$ en $-1$ et en $+\infty$.
2. Etablir le tableau de variation de $f$ sur $]-1;+\infty[$.
3. Déterminer l'équation de la tangente en 1.
4. Déterminer le signe de $f(x)$ sur $]-1;+\infty[$
5. Déterminer l'aire de la surface délimitée par la courbe représentatif de $f$, l'axe des abscisses, et les droites d'équations $x=2$ et $x=3$ en u.a..
6. On admet que $f(x)>x^2$ pour $x\in[2;3]$. Déterminer l'aire de la surface délimitée par la courbe représentative de $f$, par la courbe d'équation $y=x^2$ et par les droites d'éqautions $x=2$ et $x=3$ en u.a.
7. L'unité graphique est de 3 cm en abscisses et de 1 cm en ordonnée; Déterminer la surface précédente en $cm^2$.