TP1 : simplification, factorisation, résolution à la découverte de xcas.

Dans ce tp , nous allons découvrir les facilités de xcas en terme de simplification, factorisation, résolution d'équation et d'inéquation.

Simplifier une expression

Simplifier les expressions suivantes :

  1. $3x(x+2)+5x^3+(1-x)^3$
  2. $\sqrt{8}+9\sqrt{2}-5\sqrt{32}$
  3. $2+\frac{3}{x+1}$

Code de déblocage de la correction :

En xcas la commande pour simplifier est "simplify(..)

simp

pour écrire la racine carrée en xcas, il faudra écrire sqrt(2)

Pour écrire la racine carrée en word, il faudra écrire \sqrt(2)

Factoriser une expression

Factoriser les expressions suivantes :

  1. $3x(x+2)+5x^3+(1-x)^3$
  2. $8+\frac{3}{x+2}-\frac{x^2+1}{x}$

Code de déblocage de la correction :

En xcas la commande pour factoriser est "factor(..)

fact

Pour écrire une fraction $\frac{numérateur}{dénominateur}$ en word, il faudra écrire
numérateur/dénominateur

Résoudre une équation

Résoudre les équations suivantes :

  1. $x^2-3x+1=0$
  2. $-8x^2-3x-1=0$
  3. $x^2-1=0$ pour $x\in]2;10[$

Code de déblocage de la correction :

En xcas la commande pour résoudre une équation ou une inéquation est "solve(2x-1=2,x)

fact

En xcas la commande pour résoudre une équation ou une inéquation sur in intervalle est "solve(2x^2-1=2,x,-1..2), Ici avec cette commande on demande à xcas de résoudre l'équation $2x^2-1=2$ avec $x\in[-1;2]$.

Quand xcas renvoie 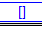factcela signifie que l'équation n'a pas de solution.

Résoudre une inéquation

Résoudre les inéquations suivantes en donnant les résultats sous forme d'intervalle:

  1. $x^2-3x+1>0$
  2. $-8x^2-3x-1<0$
  3. $-8x^2-3x-1>0$
  4. $\frac{3x-5}{x-1}\geq0$
  5. $(x+1)(3x-1)\geq0$
  6. $(x+1)(3x-1)\leq0$

Code de déblocage de la correction :

Les commentaires fait précédemment sont valables également pour les inéquations.

En xcas pour écrire $\leq$ on écrira <= et pour $\geq$ on écrira >=

Quand xcas renvoie 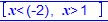factcela signifie que les solutions del'inéquation sont dans $]-\infty;-2[$ et dans $]1;+\infty[$.

Quand xcas renvoie factcela signifie que les solutions del'inéquation sont dans $]-2;1[$.

En word pour écrire $\infty$ on écrira $\infty$.

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲