TP1 Loi exponentielle

Dans ce tp , nous allons découvrir la loi exponentielle qui va nous permettre de réaliser des calculs de probabilités sur des ensembles continues.

Continues s'oppose à discrètes. Les lois binomiale qu'on a vu l'année précédente qui compte un nombre de succés prend des valeurs entières, c'est une loi discrète. Ici nous allons voir des variables aléatoires qui vont avoir des résultats qui arrivent dans des intervalles ( mesure, temps d'attente, etc..), ce sont des lois continues.

Le cours

densité de la loi exponentielle

Pour faire des calculs de probabilité avec une variable aléatoire $X$ sur des ensembles continues, il faut connaitre une fonction $f$ associé à $X$ qu'on appelle densité de $X$.

$$P(a<X<b)=P(a<X\leq b)=P(a\leq X<b)=P(a\leq X\leq b)=\int_{a}^{b}f(t) dt$$

Vous pouvez remarquer que le fait que les inégalités soient larges ou strictes ne changen pas la valeur des probabilités. Ce sera le cas pour toutes les lois continues que nous verrons(et les autres !).

On appelle loi exponentielle de paramètre $\lambda$ la loi de densité $f$ définie sur $[0;+\infty[$ par : $f_{\lambda}(t)=\lambda .e^{-\lambda .t}$

Soit $X$ une variable aléatoire qui suit une loi exponentielle de paramètre 2.

Donner une valeur approchée à $10^{-3}$ près des probabilités suivantes :

  1. $P(X\leq 1)$
  2. $P(X\geq 1)$
  3. $P(X> 5)$
  4. $P(-2\leq X < 5)$

Code de déblocage de la correction :

En xcas, je vous rappelle que pour calculer $\int_{a}^{b}f(t) dt$, vous devez écrire :

int

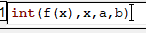
pour écrire une intégrale sous word, il faudra écrire \int_a^bf(t) dt

Espérance d'une loi exponentielle

L'espérance d'une variable aléatoire X de loi exponetielle de paramètre $\lambda$ est $$EX=\frac{1}{\lambda}$$

Soit $X$ une variable aléatoire qui suit une loi exponentielle. Calculer pour chaque paramètre l'espérance.

  1. $\lambda=2$
  2. $\lambda=\frac1{10}$
  3. $\lambda=\frac15$

Code de déblocage de la correction :

Pour écrire une fraction $\frac{numérateur}{dénominateur}$ en word, il faudra écrire
numérateur/dénominateur

Exercices

Une grande entreprise dispose d'un vaste réseau informatique. On observe le temps de fonctionnement normal séparant deux pannes informatiques. Ce temps sera appelé temps de fonctionnement.

Soit X la variable aléatoire égale au temps de fonctionnement, exprimé en heures.

On suppose que $X$ suit une loi exponentielle de paramètre 2.

  1. Calculer $P(X\leq 2)$, $P(0\leq X\leq 3)$.
  2. Déterminer $EX$.
  3. Interpréter $EX$.

Code de déblocage de la correction :

On considère une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$ dont le résultat est le temps d'attention d'un élève de BTS sur une heure de cours.

On sait que la probabilité que le temps d'attention soit inférieur à 15 minutes est de $0,8$.

Calculer $\lambda$

Code de déblocage de la correction :

On considère une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$ dont le résultat est la note obtenue d'un élève de BTS à l'examen.

On sait que l'espérance de $X$ est de 15.

Calculer $\lambda$

Code de déblocage de la correction :

  1. Soit $X$ la variable aléatoire qui suit une loi exponentielle de paramètre 2.
    1. Déterminer $P(X\leq 0,6)$.
    2. Déterminer $P(0,4\leq X\leq 0,6)$.
    3. Déterminer $P(X>0,45)$.
    4. Déterminer $E(X)$.
  2. Soit X une varaible aléatoire qui suit une loi exponentielle de paramètre $\lambda$. Déterminer $\lambda$ dans les cas suivants :
    1. $EX=\frac18$.
    2. $P(X\leq 1,5)=0,6$.

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲