Vous avez besoin pour ce chapitre des notions :
- d'angles et de cosinus : voir le chapitre sur la trigonométrie
- de calculs de coordonnées dans un repère
Demandez le programme !

Le cours
Définition du produit scalaire
Quelques définitions et propriétés essentielles.
Norme d'un vecteur
Soit $\overrightarrow{u}$ un vecteur du plan et $A$ et $B$ deux points du plan tels que $\overrightarrow{u}=\overrightarrow{AB}$.
On appelle norme du vecteur $\overrightarrow{u}$ la longueur du segment $[AB]$.
Notations : $||\overrightarrow{u}||= ||\overrightarrow{AB}||=AB$
Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs du plan. On apelle produit scalaire des vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ le nombre réel défini comme suit :
- notation $\overrightarrow{u}.\overrightarrow{v}$
- $\overrightarrow{u}.\overrightarrow{v}=||\overrightarrow{u}|| \times ||\overrightarrow{v}|| \times cos(\overrightarrow{u},\overrightarrow{v})$
- $\overrightarrow{u}.\overrightarrow{v}=0$ si l'un au moins des deux vecteurs est nul.
En guise d'exemples, une vidéo d'exemples :
Pour tout vecteur $\overrightarrow{u}$, on a : $\overrightarrow{u}^2=\overrightarrow{u}.\overrightarrow{u}=||\overrightarrow{u}||^2$
Pour tous vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ et pour tout réel $k$, on a :
- $\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}$
- $\overrightarrow{u}.(\overrightarrow{v}+\overrightarrow{w})=\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{w}$
- $\overrightarrow{u}.(k\times\overrightarrow{v})=k\times \overrightarrow{u}.\overrightarrow{v}$
Vecteurs orthogonaux
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux si l'un d'entre eux est nul ou si leurs directions sont perpendiculaires.
Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux si et seulement si leur produit scalaire est nul.
Formule géométrique
Soit $A$, $B$ et $C$ trois points du distincts du plan deux à deux. On a la formule suivante :
$\overrightarrow{AB}.\overrightarrow{AC}=AB \times AC\times cos(\widehat{BAC})$
Expression analytique du produit scalaire
On se place maintenant dans un plan muni d'un repère orthonormé $(O,\overrightarrow{i},\overrightarrow{j})$.
$(O,\overrightarrow{i},\overrightarrow{j})$ est un repère orthonormé si et seulement si
- $\overrightarrow{i}$ et $\overrightarrow{j}$ sont orthogonaux
- $||\overrightarrow{i}||=||\overrightarrow{j}||$
Expression analytique
Soit $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ deux vecteurs du plan. On a la formule
$$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'$$
Soit $\overrightarrow{u}(-1;3)$ et $\overrightarrow{v}(4;0)$ deux vecteurs du plan.
$\overrightarrow{u}.\overrightarrow{v}=-1\times4+3\times0=4+0=4$
Norme d'un vecteur
Soit $\overrightarrow{u}(x;y)$, on a la formule suivante :
$$||\overrightarrow{u}||=\sqrt{x²+y²}$$
Soit $\overrightarrow{u}(-1;3)$. $||\overrightarrow{u}||=\sqrt{(-1)²+3²}=\sqrt{1+9}=\sqrt{10}$
Attention à bien utiliser des parenthèses lorsque l'une des coordonnées est négative.
Vecteurs orthogonaux
Deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ sont orthogonaux si et seulement si $\overrightarrow{u}.\overrightarrow{v}=xx'+yy'=0$
Une vidéo pour vous aider :
Projeté orthogonal
Soit la droite $(AB)$ et un point C n'appartenant pas à la droite $(AB)$. Le point $H$ est le projeté orthogonal du point $C$ sur la droite $(AB)$ si :
- $(CH)$ est perpendiculaire à $(AB)$
- $H$ appartient à la droite $(AB)$

Soit $A$, $B$ et $C$ trois points non alignés du plan et $H$ le projeté orthogonal du point $C$ sur la droite $(AB)$.
- Si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AH}$ sont colinéaires et de même sens, alors $\overrightarrow{AB}.\overrightarrow{AC}=AB \times AH$
- Si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AH}$ sont colinéaires et de sens contraires, alors $\overrightarrow{AB}.\overrightarrow{AC}=-AB \times AH$
On a dans ce cas $AH=AC \times cos(\widehat{HAC})$ que l'on peut écrire $||\overrightarrow{AH}||=||\overrightarrow{AC}|| \times cos(\overrightarrow{AH},\overrightarrow{AC})$
Théorème d'Al-Kashi
Le théorème d'Al-Kashi est la généralisation du théorème de Pythagore.
On considère le triangle $ABC$ avec les notations suivantes : $a=BC$, $b=AC$ et $c=AB$
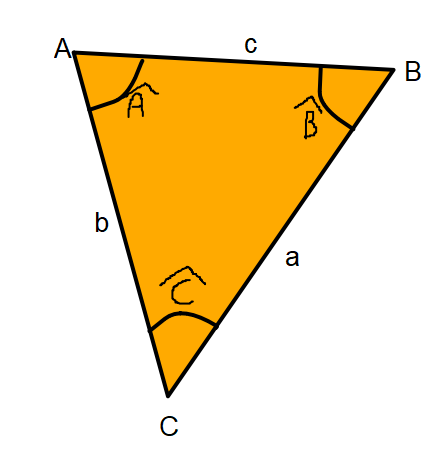
Dans le triangle $ABC$ défini ci-dessus, on a les formules suivantes :
- $a²=b²+c² -2bc\times cos(\widehat{A})$
- $b²=a²+c² -2ac\times cos(\widehat{B})$
- $c²=b²+a² -2ba\times cos(\widehat{C})$
Si le triangle $ABC$ est rectangle en A, alors $cos(\widehat{A})=0$. On retrouve le théorème de Pythagore : $a²=b²+c²$
Les ressources et exercices
Calculatrice numworks disponible : le site numworks
Exercices méthodes
Pour les exercices 1,3 et 5 : vous pouvez regarder la vidéo de l'exemple 1.
Accès direct
Calculer $\overrightarrow{u}.\overrightarrow{v}$ dans les cas ci-dessous :
- $||\overrightarrow{u}||=3$, $||\overrightarrow{v}||=2$ et $(\overrightarrow{u},\overrightarrow{v})=\frac{3\pi}{4}$
- $||\overrightarrow{u}||=3$, $||\overrightarrow{v}||=2$ et $(\overrightarrow{u},\overrightarrow{v})=\frac{5\pi}{6}$
- $||\overrightarrow{u}||=3$, $||\overrightarrow{v}||=2$ et $(\overrightarrow{u},\overrightarrow{v})=\frac{3\pi}{2}$
- $||\overrightarrow{u}||=3$, $||\overrightarrow{v}||=2$ et $(\overrightarrow{u},\overrightarrow{v})=-\frac{\pi}{3}$
- $||\overrightarrow{u}||=3$, $||\overrightarrow{v}||=2$ et $(\overrightarrow{u},\overrightarrow{v})=\pi$
On considère un triangle équilatéral CAT de côté 4 et I le milieu de [TA]
- Faire un croquis de l'exercice
- Calculer les produits scalaires :
- $\overrightarrow{CA}.\overrightarrow{CT}$
- $\overrightarrow{IT}.\overrightarrow{IA}$
- $\overrightarrow{TI}.\overrightarrow{TA}$
- $\overrightarrow{TI}.\overrightarrow{TC}$
Une vidéo qui ne donne pas la solution mais qui aide :
On donne $||\overrightarrow{u}||=5$, $||\overrightarrow{v}||=3,5$ et $\overrightarrow{u}.\overrightarrow{v}=6$
Calculer $(\overrightarrow{u},\overrightarrow{v})$
On donne $||\overrightarrow{u}||=2$, $(\overrightarrow{u},\overrightarrow{v})=\frac{\pi}{3}$ et $\overrightarrow{u}.\overrightarrow{v}=8$
Calculer $||\overrightarrow{v}||$
On considère le plan muni d'un repère orthonormé $(O,\overrightarrow{i},\overrightarrow{j})$.
On considère les vecteurs : $\overrightarrow{u}(-1;3)$ et $\overrightarrow{v}(5;2)$.
Calculer $\overrightarrow{u}.\overrightarrow{v}$
Un rappel en vidéo pour les vecteurs :
On considère le plan muni d'un repère orthonormé $(O,\overrightarrow{i},\overrightarrow{j})$.
On considère les points : $A(0;2)$, $B(-1;-1)$ et $C(2;-1)$.
Calculer $\overrightarrow{AB}.\overrightarrow{AC}$ et $\overrightarrow{AB}.\overrightarrow{BC}$
On considère le plan muni d'un repère orthonormé $(O,\overrightarrow{i},\overrightarrow{j})$.
On considère les vecteurs : $\overrightarrow{u}(-1;1)$ et $\overrightarrow{v}(2;2)$.
Les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont-ils orthogonaux ?
On considère le plan muni d'un repère orthonormé $(O,\overrightarrow{i},\overrightarrow{j})$.
On considère les points : $A(-1;2)$, $B(1;-1)$ et $C(2;-1)$.
Les droites $(AB)$ et $(AC)$ sont-elles perpendiculaires ?
Vous pouvez utiliser (pour vérifier) l'espace géogébra accessible ICI
On considère le plan muni d'un repère orthonormé $(O,\overrightarrow{i},\overrightarrow{j})$.
On considère les points : $A(-1;2)$, $B(1;-1)$ et $C(2;-1)$.
- Calculer $\overrightarrow{AB}.\overrightarrow{AC}$.
- En utilisant la formule du cours $\overrightarrow{AB}.\overrightarrow{AC}=AB \times AC\times cos(\widehat{BAC})$, en déduire
la valeur de $cos(\widehat{BAC})$
- Quelle est la valeur de $\widehat{BAC}$ ?
Vous pouvez utiliser (pour vérifier) l'espace géogébra accessible ICI
La solution en vidéo
On considère le triangle $ABC$ tel que $AC=4$, $BC=6$ et $\widehat{BCA}=49°$
Ecrire les trois formules d'Al Kashi pour ce triangle.
Calculer $AB$ en utilisant une des trois formules.
La solution en vidéo
On considère le triangle $ABC$ équilatéral tel que $AC=5$
En utilisant le théorème d'Al Kashi, retrouver le fait que $\widehat{BCA}=60°$
La solution en vidéo
Espace GEOGEBRA
Pour tester vos formules analytiques :
Le produit scalaire avec sa définition analytique :
Le produit scalaire et le projeté orthogonal :
TD à télécharger
Feuille d'exercices créé à partir des "warm up". Correction à la fin de la feuille
TD construis à partir du site "chingatome" accès direct
TD avec les qrcodes de correction.
TD avec la correction
Vidéos supplémentaires
Le contrôle et sa correction en vidéo :