Cours

Enroulement de la droite des réels sur le cercle trigonométrique

Le plan est muni d'un repère orthonormé $(O,\vec{i},\vec{j})$, ,$I$ est le point tel que $\overrightarrow{OI}=\vec{i}$ et $J$ est le point tel que $\overrightarrow{OJ}=\vec{j}$.

Le cercle trigonométrique est un cercle de rayon 1, sur lequel on définit un sens positif de parcours : c'est le sens inverse des aiguilles d'une montre. On parle de sens direct.

On considère le cercle trigonométrique $C$ de centre O . Le périmètre de ce cercle est donc égal à $2\pi$. La droite $(d)$, tangente à $C$ en I, est munie du repère $(I;\vec{j})$ : cette droite s'appellera la droite des réels. Sur cette droite, on place un point X d'abscisse $x$. Imaginez que l'on enroule cette droite sur le cercle trigonométrique. Chaque point $X$ vient correspondre à un unique point $M$ du cercle. Ce point est alors appelé le point associé au nombre $x$.

Dans l'animation ci-dessous, vous pouvez bouger le point $M$ du cercle. La longueur de l'arc $\overset{\displaystyle\frown}{AM}$ sur le cercle correspond à la longueur $AX$ sur la droite.

Soit $M$ un point du cercle trigonométrique associé à un nombre réel $x$.

En utilisant les points de l'application GEOGEBRA, retrouver les valeurs associées aux points de $M_{0}$ à $M_{15}$.

Explications en vidéos :

On enroule la droite des réels sur le cercle trigonométrique $C$ de centre O. Déterminez les points respectivement associés aux nombres réels $x_1=\frac{19\pi}{3}$ et $x_2=-\frac{21\pi}{4}$

La correction en vidéo.

Les nombres réels $x_1=\frac{19\pi}{3}$ et $x_2=\frac{53\pi}{3}$ sont-ils associés au même point sur le cercle trigonométrique ?

Même question avec les réels $x_1=-\frac{12\pi}{7}$ et $x_2=\frac{30\pi}{7}$

La correction en vidéo.

Une nouvelle unité de mesure d'angle : le radian

Mesure en radians d'angles géométriques

Soit $U$ le point du cercle trigonométrique associé au réel 1. On définit 1 radian (1 rad) comme la mesure de l'angle géométrique $\widehat{IOU}$.
Soit $x$ un nombre réel appartenant à l'intervalle $[0;\pi]$ et $M$ le point du cercle trigonométrique de centre $O$ associé à $x$. $x$ est appelé la mesure en radians de l'angle géométrique $\widehat{IOM}$.

Le point $M_3$ est le point associé au nombre $\frac{\pi}{3}$, l'angle $\widehat{IOM_3}$ a pour mesure $\frac{\pi}{3}$ rad.
Les mesures en degrés et en radians d'un angle géométrique sont proportionnelles.
Retenez la correspondance entre 180 degrés et $\pi$ radians.

Mesures en radians des angles orientés de vecteurs

L'angle géométrique $\widehat{IOM_3}$ s'appelle également $\widehat{M_3OI}$. La distance sur le cercle pour se rendre d'un point à l'autre est la même, par contre le sens est différent. Pour tenir compte du sens (direct ou indirect), nous allons définir la notion d'angle orientée de vecteurs.

Soit $x$ un nombre réel et $M$ le point du cercle trigonométrique de centre $O$ associé à $x$. On dit que $x$ est une mesure en radians de l'angle orienté de vecteurs $(\overrightarrow{i},\overrightarrow{OM} )$
L'angle orienté $(\overrightarrow{i},\overrightarrow{OM} )$ admet une infinité de mesures en radians que l'on peut écrire sous la forme $x+k2\pi$ où $k$ est un entier relatif ($k$ correspond aux "nombres de tours d'enroulement")

Mesure principale d'un angle orienté de vecteurs

La mesure principale d'un angle orienté de vecteurs est l'unique mesure d'un angle appartenant à l'intervalle $]-\pi;\pi]$.

Dans notre cercle trigonométrique, $\frac{\pi}{6}$, $\frac{-11\pi}{6}$, $\frac{25\pi}{6}$, $\frac{13\pi}{6}$; ... sont des mesures de l'angle orienté de vecteurs $(\overrightarrow{i},\overrightarrow{OM_1} )$. La mesure principale de cet angle est $\frac{\pi}{6}$.

Correction en vidéo :

Déterminer la mesure principale d'un angle orienté dont une mesure est $\frac{41\pi}{6}$

Correction en vidéo :

Cosinus et sinus d'angles orienté de vecteurs

Définitions et valeurs remarquables

Soit $M$ un point du cercle trigonométrique de centre $O$ et $x$ une mesure en radians de l'angle orienté de vecteurs $(\overrightarrow{i},\overrightarrow{OM} )$.

Voici un ensemble de valeurs exactes à connaître. Ces valeurs sont présentées dans ce tableau que l'on appelle souvent : "le tableau des valeurs remarquables"

Mesure en radians $x$ de l'angle orienté $0$ $\frac{\pi}{6}$ $\frac{\pi}{4}$ $\frac{\pi}{3}$ $\frac{\pi}{2}$
cos $x$ $1$ $\frac{\sqrt{3}}{2}$ $\frac{\sqrt{2}}{2}$ $\frac{1}{2}$ $0$
sin $x$ $0$ $\frac{1}{2}$ $\frac{\sqrt{2}}{2}$ $\frac{\sqrt{3}}{2}$ $1$

Déterminez les valeurs exactes de $cos(\frac{-\pi}{4})$, $sin(\frac{-\pi}{4})$, $cos(\frac{2\pi}{3})$, $sin(\frac{2\pi}{3})$, $cos(\frac{7\pi}{6})$ et $sin(\frac{7\pi}{6})$

Propriétés

Pout tout nombre réel $x$,

Angles associés

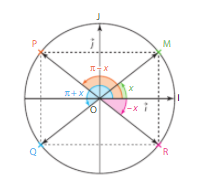
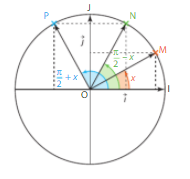
Pout tout nombre réel $x$,

On donne $cos(\frac{\pi}{12})=\frac{\sqrt{6}+\sqrt{2}}{4}$ et $sin(\frac{\pi}{12})=\frac{\sqrt{6}-\sqrt{2}}{4}$. En déduire les valeurs exactes de $sin(\frac{11\pi}{12})$, $cos(\frac{13\pi}{12})$, $cos(\frac{5\pi}{12})$, $sin(\frac{72\pi}{12})$,

Equations trigonométriques

Avec cosinus

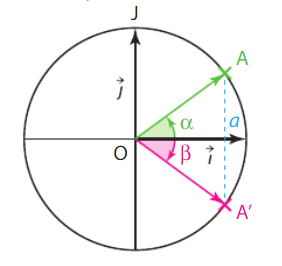
Soit $\alpha$ une mesure en radians de l'angle orienté $(\overrightarrow{i},\overrightarrow{OA} )$. L'équation $cosx=a$ admet comme solutions l'ensemble des valeurs noté $x=\alpha+k2\pi$ avec $k$ entier rlatif.

Avec sinus

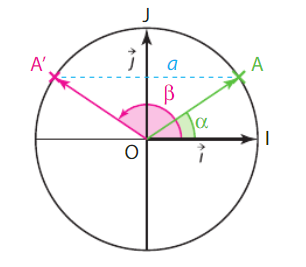
Soit $\beta$ une mesure en radians de l'angle orienté $(\overrightarrow{i},\overrightarrow{OA} )$. L'équation $sinx=a$ admet comme solutions l'ensemble des valeurs noté $x=\pi-\alpha+k2\pi$ avec $k$ entier rlatif.

Résoudre dans $\mathbb{R}$ l'équation $cos x=-\frac{\sqrt{3}}{2}$

Résoudre dans $\mathbb{R}$ l'équation $sin x=\frac{\sqrt{2}}{2}$

Résoudre dans $]-\pi;2\pi]$ l'équation $cos x=\frac{-1}{2}$

La solution en vidéo :

Fonctions trigonométriques

Vous pouvez aller voir le générateur de fonctions $cosinus$ et $sinus$ avec GEOGEBRA ICI

Une vidéo qui présente le générateur

Les fonctions $cosinus$ et $sinus$ sont des fonctions périodiques de périodes $2\pi$. Les courbes représentatives des fonctions $cosinus$ et $sinus$ sont reproduites tous les $2\pi$.

Une vidéo pour trouver graphiquement la période d'une fonction.

La fonction $cosinus$ est une fonction paire. La courbe représentative de la fonction $cosinus$ est symétrique par rapport à l'axe des ordonnées.

La fonction $sinus$ est une fonction impaire. La courbe représentative de la fonction $sinus$ est symétrique par rapport à l'origine du repère.

Trouver la période de la fonction représentée ci-dessous :

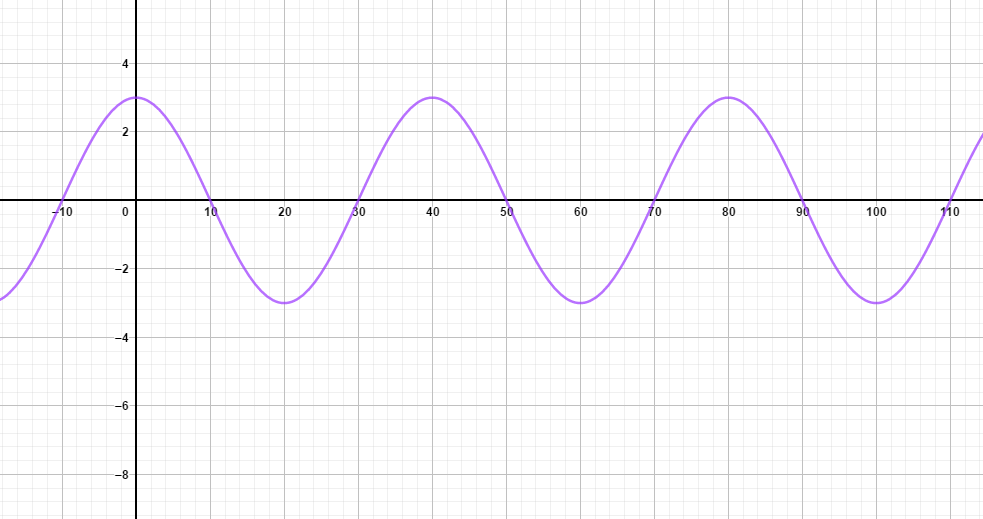
Vous pouvez utiliser les curseurs pour visualiser différentes sinusoïdales.

Trouver la périodicité de chaque courbe.

Ressources interactives

Sur le web

Le site "Le matou matheux" propose des animations intéressantes :

Espace Python

Si vous voulez utiliser le langage python pour faire des calculs, vous pouvez utiliser cet espace :

Espace GEOGEBRA

Valeurs du cosinus et sinus d'un angle dans le cercle trigonométrique.

En utilisant l'exemple 3, retrouvez les valeurs des $cosinus$ et $sinus$ des angles du tableau des valeurs remarquables.

Générateur des fonctions $cos(x)$ et $sin(x)$ à partir du cercle trigonométrique.

En utilisant l'exemple 4, retrouvez les propriétés des fonctions $cosinus$ et $sinus$.

TD à télécharger

Voici une liste de ressources réalisées sur le site "chingatome" (feuilles autocorrectives) :

Généralités sur la trigonométrie

D'autres ressources :



Espace logiciels

Vous pouvez utiliser des logiciels de calcul formel. Il en existe plusieurs, je vous conseille :

Vous avez à disposition un espace créé qui traite du logiciel xcas (voir la page d'accueil de la spécialité)

Espace vidéos

Les vidéos sont incorporées dans le site et les exercices.

▲