Avant -propos
Cette page sert à acquérir la notion de boucle répétitive en algorithmique et son implémentation dans le langage Python.
Cette page contient :
-
De vidéos qui permettent de reprendre chez vous des points sur lesquels vous ne vous sentez pas très à l'aise ou pour vous
remémorer le contenu.
-
Des rappels écrits des notions avec des exemples,
-
Des exercices fondamentaux, ceux où apparaissent la balise "fondamental", à savoir faire en seconde,
-
Des exercices de renforcement, ceux en fin de page où apparaissent la balise "renforcement" et accessible directement par un lien,
pour s'assurer que les exercices fondamentaux sont maîtrisés ; tous ces exercices de renforcement possèdent une correction
librement disponible depuis le site,
-
Quelques exercices plus poussés, ceux étiquetés par la balise "confirmé".
C'est ce niveau d'exercices qu'il faut essayer d'atteindre en fin de seconde.
Si votre jupyter ne fonctionne pas, vous pouvez utiliser cet espace pour tester vos scripts, sans pouvoir les y enregistrer :
Découverte
Considérons la fonction $f$ définie sur $[0;9]$ par $f(x)=x^2\times(8-x)$.
On voudrait compléter un tableau de valeurs comme celui ci-dessous :
|
$x$
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
$f(x)$
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
Comme le travail est répétitif, il suffit d'utiliser une boucle for dans un script comme celui-ci afin d'obtenir l'affichage des
diffférentes images voulues :
for i in range(0,10): # 10 pour un arrêt avec i=9
image = i**2*(8-i)
print(image)
Il est possible de structurer ce script pour séparer la partie déinition de la fonction (mathématique) de la partie utilisation.
# définition de la fonction appelée ici f
def f(x) :
return (x**2)*(8-x)
# Utilisation de cette fonction f dans un programme
for i in range(10) :
print(f(i))
En structurant ainsi, on fait appel à la notion de fonction en informatique : c'est le bloc commençant par le mot-clé
def.
Au collège, vous avez peut-être déjà vu et utilisé cette notion de fonction en utilisant le bloc
 présent dans
présent dans  :
:
Voici la correspondance entre le programme précédent écrit en Python et un script équivalent en Scratch2 :

Fonction en informatique
Formalisation simplifiée
Donnons une vision simplifiée de la notion de fonction :
La notion de fonction en informatique est comparable à la notion de fonction en mathématiques :
elle prendune valeur de départ appelée paramètre et renvoie une valeur.
Vision mathématique : 
Vision informatique : 
Définir une fonction en Python
La syntaxe pour définir une fonction en Python est celle ci :
def nomDeLaFonction(parametre):
instruction 1
instruction 2
...
return retourDeLaFonction
Prenons la fonction $f:x\longmapsto x^2$.
si vous voulez implémenter cette fonction en Python, il suffira d'écrire :
def f(x):
return x**2
Pour calculer l'image de 3 , en mathématiques vous feriez $f(3)$ , en Python c'est pareil !
Il suffit de saisir :
f(3)
Tester le script de l'exemple précédent ainsi que le calcul d'image.
-
Créer une fonction cube qui prend comme paramètre un flottant x et qui renvoie le cube de ce nombre.
-
Utiliser cette fonction dans une boucle répétitive écrite en Python afin de compléter le tableau de valeurs ci-dessous :
|
$x$
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|
$x^3$
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
-
Que pouvez-vous conjecturer quant à la comparaison de $x$ et de $x^3$ lorsque $x$ appartient à l'intervalle $[0;1]$ ?
exercice de renforcement
Attention à bien faire la différence entre print et return :
-
-
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x^2+2x+5$.
-
Aller sur le site capytale afin de charger l'exercice référencé par le code suivant : 60b3-15719.
-
Créer une fonction f qui prend comme paramètre un flottant x et qui renvoie l'image $x^2+2x+5$ de ce nombre par $f$.
-
Utiliser cette fonction f dans un script1 qui permet d'obtenir l'ensemble des images de x pour x entier variant
entre 0 et 10.
-
Laisser le script1 comme commentaire avec le symbole #.
Comment modifier ce script1 en un script 2 pour que x désormais varie entre 0 et 1 avec un pas de 0.1 ? Le faire.
Le programme écrit ci-dessous en langage Python permet de définir une fonction $f$ :
def f(x) :
if x<1 :
y=x**2
else :
y=2*x-1
return y
-
Quelle valeur est retournée lorsque l'on saisit dans la console :
-
$f(2)$ ?
-
$f(0)$ ?
-
$f(-5)$ ?
-
$f(1.5)$ ?
-
$f(1)$ ?
-
-
Déterminer l'expression de $f(x)$ lorsque $x$ appartient à l'intervalle $]-\infty;1[$.
-
Déterminer l'expression de $f(x)$ lorsque $x$ appartient à l'intervalle $[1;+\infty[$.
On considère la fonction $g$ définie sur $\mathbb{R}$ par $g(x)=1−2x^3$ si $x\le 0$ et $g(x)=4x+5$ si $x>0$.
En adaptant le programme de l'exercice précédent, proposer un algorithme écrit en langage Python qui permet d'obtenir cette fonction $g$.
Un magasin de location de scooters affiche les tarifs ci-dessous :
|
Moins de 8 heures : 1.80€ l'heure et 1.50€ de frais de dossier
À partir de 8 heures : 1.50€ l'heure et 3€ de frais de dossier
|
-
Calculer le prix à payer pour :
-
5 heures de locations.
-
10 heures de locations.
-
On note $p$ la fonction qui, au nombre $x$ d'heures de location, associe le prix à payer (en euros).
Déterminer l'expression de $p(x)$ suivant les valeurs de $x$.
-
Dans le programme écrit en langage Python ci-dessous, la fonction prix doit retourner le prix à payer pour $x$ heures de locations.
Compléter ce programme et le tester sur Edupython avec les valeurs $x=5$ et $x=10$.
def prix(x) :
if ...........
p=..............
else :
................
....................
-
Proposer un script qui utilise la fonction prix précédente et qui affiche chacun des prix à payer pour une location de 30 minutes,
de 1 heure, de 1h30, de 2h, ..., de 23h30, de 24h.
exercice de renforcement
Formalisation générale
Plus généralement, on peut simplifier l'écriture de des programmes en utilisant des fonctions, des sortes de sous-programmes.
Ces fonctions permettent :
-
de décomposer une tâche complexe en tâches plus simples traitées indépendamment,
-
d'éviter la répétition d'une portion d'algorithme qui doit être exécutée plusieurs fois,
-
de pouvoir réutiliser une tâche routinière dans d'autres algorithmes.
Si l'on veut savoir si un triangle est rectangle ou pas à partir de la seule connaissance de ses trois longueurs, on peut créer un
algorithme où la partie calculatoire est mise dans une fonction séparée :
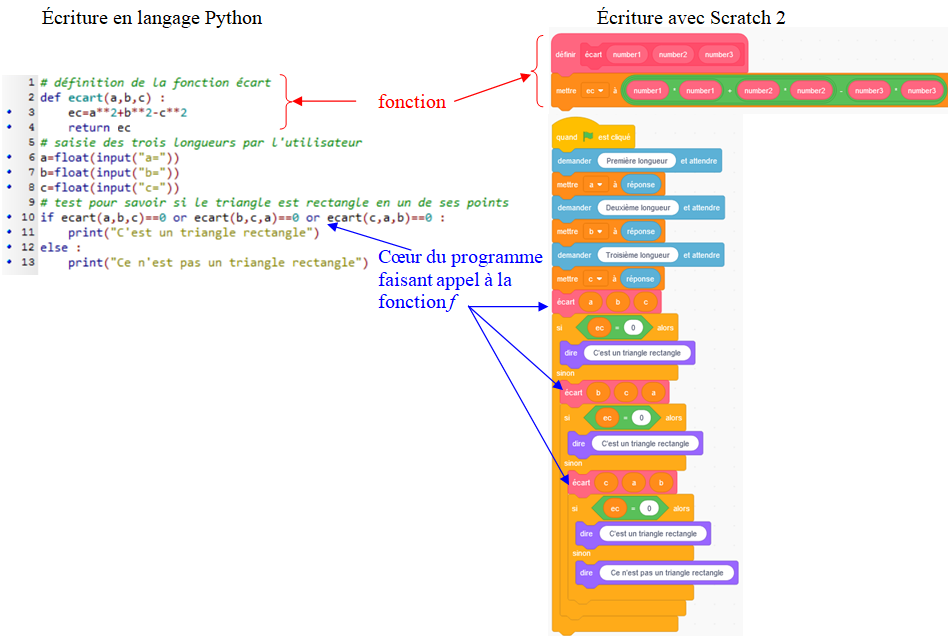
Ici, la fonction ecart donne l'écart au résultat attendu par le théorème de Pythagore ; elle permet bien :
-
de traiter séparément les calculs,
-
d'éviter à écrire trois fois le même code (pour étudier chacun des sommets)
-
de pouvoir récupérer ce bout de code pour l'intégrer dans un autre script, par exemple, pour savoir si un parallélogramme est
un rectangle ou non.
Cette fonction prend 3 arguments en entrée : les trois longueurs du triangle.
Une fonction est un bloc d'instructions :
-
qui a reçu un nom,
-
dont le fonctionnement dépend d'un certain nombre de paramètres (les arguments),
-
qui peut renvoyer (=retourner) un résultat (au moyen de l'instruction return).
La syntaxe pour définir une fonction en Python est celle ci :
def nomDeLaFonction(argument1,argument2,...): # une fonction peut avoir plusieurs paramètres d'entrée
instruction 1
instruction 2
...
...
...
return retourDeLaFonction
def ecart(a,b,c) :
ec=a**2+b**2-c**2
return ec
Dans la fonction ecart de l'exemple précédent :
-
Quel est le nom de la fonction ?
-
Quels sont les arguments de la fonction ?
-
Quel est le résultat renvoyé ?
Proposer une fonction addition qui prend en paramètres deux nombres entiers a et b et qui renvoie
la somme de ces deux nombres.
exercice de renforcement
Il est possible de renvoyer non seulement le contenu d'une variable mais aussi directement le résultat d'opérations.
-
Proposer une fonction, nommée mini2 qui prend comme arguments deux nombres entiers a et b et qui renvoie
le minimum de ces deux nombres.
-
Proposer une fonction, nommée mini4, qui :
-
prend comme arguments quatre nombres entiers
a, b, c et d,
-
fait appel plusieurs fois à la fonction mini2 pour finalement trouver le minimum des quatre nombres
-
renvoie le minimum trouvé.
exercice de renforcement
Un site en ligne propose une promotion sur des téléphones portables suivant les cas suivants :
-
Si l'appreil coûte moins de 200€, la promotion est de 10% (cela revient à dire que le prix initial est multiplié par 0.9 pour obtenir le prix
après réduction).
-
Si l'appreil coûte plus de 200€, la promotion est de 20%.
-
Proposez une fonction promotion qui prend comme argument le prix initial et qui renvoie le prix en prenant en compte la promotion.
-
Les frais de port de 10€ sont offerts si le montant de la commande, après promotion (mais hors frais de port) est strictement supérieur à 100€.
Proposez une fonction payer qui :
-
demande le prix initial,
-
utilise la fonction promotion pour déterminer le prix après promotion,
-
prend en compte l'éventuelle offre des frais de port,
-
renvoie le prix final à payer.
-
Testez votre programme avec quelques prix initiaux. Par exemple, avec 50€, 100€, 200€, 1000€, ...
exercice de renforcement
Un site en ligne de développer des photos numériques et de les envoyer aux clients. Le tarif dépend des cas suivants :
-
Si vous demandez moins de 100 développements de photos, chaque photo coûte 0.10€.
-
Si vous demandez au moins 100 développements de photos, chaque photo coûte 0.08€.
-
Aller sur le site capytale afin de charger l'exercice référencé par le code suivant : 8312-17313.
-
Proposez une fonction developper qui prend comme argument le nombre de photos développées et qui renvoie le coût total.
-
Les frais de port de 6.30€ sont offerts si le montant de la commande est strictement supérieur à 30€.
Proposez une fonction payer qui :
-
prend comme paramètre d'entrée le nombre de photos développer en tout,
-
détermine le coût du développement,
-
étudie le coût éventuel de l'envoi,
-
renvoie le prix final à payer pour le développement et l'envoi.
Utiliser dans cette fonction payer, la fonction developper.
-
Testez votre programme avec quelques prix initiaux. Par exemple, avec 10, 100, 200, 1000, ... photos
Exercices
Un étudiant a emprunté 1000€ à une amie et envisage de remboursé 65€ par mois.
On note $x$ le nombre de mois écoulés depuis le début du remboursement.
-
Proposer une fonction reste qui prend en paramètre un réel x et qui renvoie la somme que cet étudiant doit
encore rembourser au bout de $x$ mois.
-
Dans un second temps, faire en sorte que la fonction renvoie 0 s'il ne reste plus rien à remboruser.
Écrire une fonction signe_prod(a,b) qui reçoit deux entiers a et b relatifs et qui renvoie True
si le produit de a par b est strictement positif et False sinon. Attention : on ne doit pas calculer le produit des deux nombres.
L'Indice de Masse Corporelle (IMC) est un indicateur chiffré utilisé en médecine.
L'IMC d'une personne est donné par la formule $ IMC= \frac{masse}{taille^2}$ où la masse est en kilos et la taille en mètres.
Proposez une fonction IMC prend en paramètres la taille et la masse et qui renvoie l'IMC de la personne.
La surface $S$ en mètre carrés de la peau d'un adulte est donnée approximativement par la formule
$ \dfrac{\sqrt{L\times M}}{6}$ où $L$ est la taille de l'individu en mètres et $M$ sa masse en kilogramme.
Vous devez créer ci-dessous une fonction en Python.
Votre fonction doit :
Importer la fonction sqrt de la bibliothèque math en commençant votre code par la ligne suivante :
from math import sqrt
Vous pourrez ainsi utiliser la fonction racine carrée en saisissant sqrt() et en insérant dans les parenthèses le nombre
dont vous voulez calculer la racine carrée.
a=sqrt(4)
conduit au stockage du nombre 2 dans la variable
a.
-
Le programme de la fonction donné ci-dessous doit simuler 50 lancers successifs d'une pièce de monnaie équilibrée.
La variable P compte le nombre de "Pile" obtenus.
Compléter ce programme.
La première ligne permet d'utiliser les fonction du module random ; en particulier randint(0,1) renvoie
soit 0, soit 1 avec une probabilité de $\dfrac{1}{2}$.
from random import *
def nb_pile() :
P = 0
for i in range(... , ...) :
R = randint(0,1)
P = ...
return ...
-
Quelles modifications suffit-il d'apporter à cette fonction afin qu'elle retourne la fréquence de "Pile" obtenus ?
Le faire pour créer une fonction freq_pile.
-
Quelles modifications suffit-il d'apporter à cette fonction nb_pile afin qu'elle simule $n$ lancers successifs ?
Le faire.
On considère les deux fonctions suivantes :
def f(a,b):
return 2*a-b
def g(a,b):
return a*b+1
On considère la fonction h faisant appel aux deux fonctions précédentes :
def h(a,b):
a = f(a,b)
b= g(a,b)
return f(a,b)
Donner l'expression renvoyée par h en fonction de $a$ et de $b$.
Exercices de renforcement
-
Créer une fonction inverse qui prend comme paramètre un flottant x non nul et qui renvoie l'inverse $\dfrac{1}{x}$
de ce nombre.
-
Utiliser cette fonction dans une boucle répétitive écrite en Python afin de compléter le tableau de valeurs ci-dessous :
|
$x$
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
$\dfrac{1}{x}$
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
-
Que pouvez-vous conjecturer aux variations de la fonction $x\mapsto \dfrac{1}{x}$ sur l'intervalle $[1;10]$ ?
Cliquer pour afficher la solution
-
Voici la fonction inverse qui prend comme paramètre un flottant x non nul et qui renvoie le cube de ce nombre :
def inverse(x) :
return 1/x
-
Utiliser cette fonction dans une boucle répétitive afin de compléter le tableau de valeurs ci-dessous :
for i in range(1,11): # 11 pour 10 répétitions (de 1 à 10) afin d'aller de 0.1 à 1 avec un pas de 0.1
print(inverse(i*0.1))
On obtient ainsi le tableau de valeurs ci-dessous (en arrondissant pour ne pas prendre en compte les approximations de calcul lié à
l'utilisation de nombres flottants au lieu de nombres entiers) :
|
$x$
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
$\dfrac{1}{x}$
|
1 |
0.5 |
0.33333333 |
0.25 |
0.2 |
0.16666666 |
0.14285714 |
0.125 |
0.11111111 |
0.1 |
-
La fonction invese semble être strictement décroissante sur $[0;10]$.
Une association propose d'aider des personnes à apprendre à réparer leur vélo. Outre le prix des pièces, l'association propose deux tarifs :
-
tarif A : prendre une adhésion à 10€ à l'association et payer 1€ par heure passée avec un membre de l'association pour la réparation,
-
tarif B : sans adhésion à l'association mais payer 4.50€ par heure passée avec un membre de l'association pour la réparation.
-
Calculer le prix à payer pour :
-
3 heures de réparations pour une personne prenant une adhésion à l'association.
-
4 heures de réparations pour une personne ne prenant pas d'adhésion à l'association.
-
-
On note $p1$ la fonction qui, au nombre $x$ d'heures de réparation, associe le prix à payer (en euros), hors pièces, dans le cas d'une
adhésion à l'association.
Déterminer l'expression de $p1(x)$ suivant les valeurs de $x$.
-
Écrire en langage Python une fonction p1 doit retourner le prix à payer pour $x$ heures de réparation, hors pièces,
dans le cas d'une adhésion à l'association.
Le tester sur Edupython avec la valeur $x=3$.
-
-
On note $p2$ la fonction qui, au nombre $x$ d'heures de réparation, associe le prix à payer (en euros), hors pièces, dans le cas où
aucune adhésion n'est prise.
Déterminer l'expression de $p2(x)$ suivant les valeurs de $x$.
-
Écrire en langage Python une fonction p2 doit retourner le prix à payer pour $x$ heures de réparation, hors pièces,
dans le cas où aucune adhésion n'est prise.
Le tester sur Edupython avec la valeur $x=4$.
-
Proposer un script qui utilise la fonction p1 précédente et qui affiche chacun des prix à payer pour 1 heure, de 2h, ..., 12h de
répération dans le cas d'une adhésion.
-
Proposer une fonction choisir qui utilise les fonctions p1 et p1 précédentes qui prend comme parammètre
le nombre d'heures prévues x pour la réparation, qui affiche le nom du tarif le plus avantageux et qui renvoie
le prix à payer avec ce tarif.
Ne pas confondre print et return !
Cliquer pour afficher la solution
-
Calculer le prix à payer pour :
-
3 heures de réparations pour une personne prenant une adhésion à l'association est de 13€ : 10 euros pour l'adhésion et 3 € pour le temps
passé.
-
4 heures de réparations pour une personne ne prenant pas d'adhésion à l'association est de 18€ car $4\times 4.5=18$.
-
-
L'expression de $p1(x)$ sest donnée par $p1(x)=x+10$.
-
Voici la fonction p1 :
def p1(x):
return 10+x
Cette fonction p1 renvoie bien 13 lorsque son argument a pour valeur 3.
-
-
L'expression de $p2(x)$ sest donnée par $p2(x)=4.5*x$.
-
Voici la fonction p2 :
def p2(x):
return 4.5*x
Cette fonction p1 renvoie bien 18 lorsque son argument a pour valeur 4.
-
Voici un script qui utilise la fonction p1 précédente et qui affiche chacun des prix à payer pour 1 heure, de 2h, ..., 12h de
répération dans le cas d'une adhésion.
def p1(x):
return 10+x
for i in range(1,13): # la dernière valeur prise par i est 12
print(p1(i))
-
Proposer une fonction choisir qui utilise les fonctions p1 et p1 précédentes qui prend comme parammètre
le nombre d'heures prévues x pour la réparation, qui affiche le nom du tarif le plus avantageux et qui renvoie
le prix à payer avec ce tarif.
def p1(x):
return 10+x
def p2(x):
return 4.5*x
# fonction demandée ici
def choisir(x):
if p1(x)>p2(x):
print("Choisir le tarif B sans adhésion.")
prix = p2(x)
else:
print("Choisir le tarif A avec adhésion.")
prix = p1(x)
return prix
Proposer une fonction multiplier qui prend en paramètres deux nombres entiers a et b et qui renvoie
le produit de ces deux nombres.
Cliquer pour afficher la solution
def multiplier(a,b):
return a*b
On suppose que vous disposez déjà des deux fonctions mini2 et mini4 programmées dans un exercice précédent
(cf. lien direct)
Proposer une fonction, nommée
mini4, qui :
-
prend comme arguments huit nombres entiers, nommés de a à h,
-
fait appel aux fonctions mini2 et mini4 pour finalement trouver le minimum des huit nombres,
-
renvoie le minimum trouvé.
Cliquer pour afficher la solution
# définition des fonctions mini2 et mini4
def mini2(a,b):
if a>b:
return b
else:
return a
def mini4(a,b,c,d):
e=mini2(a,b)
f=mini2(c,d)
return mini2(e,f)
# fonction à créer :
def mini8(a,b,c,d,e,f,g,h):
i=mini4(a,b,c,d)
j=mini4(e,f,g,h)
return mini2(i,j)
Un magasin vend des produits bio.
Afin de promouvoir la consommation de produits bio, le magasin propose une réduction de 2% pour tout achat dépassant 50€
et de 5% pour tout achat dépassant 200€.
-
Proposez une fonction promotion qui prend comme argument le prix initial et qui renvoie le prix en prenant en compte la promotion.
-
Le magasin propose aux clients de payer 1% de plus sur la facture : cette somme étant reversée à des projets humanitaires ou écologiques.
Proposez une fonction engager qui :
-
prend en paramètre le prix initial (sans réduction ni engagement),
-
utilise la fonction promotion pour déterminer le prix après promotion,
-
demande à l'utilisateur s'il veut payer 1% de plus pour un tel projet.
Imposer la réponse attendue à l'utilisateur : "OUI" ou "NON".
-
renvoie le prix final à payer en prenant en compte l'éventuel engagement,
-
Testez votre programme avec quelques prix initiaux. Par exemple, avec 20€, 100€, 400€, ...
Cliquer pour afficher la solution
-
def promotion(prix_initial):
if prix_initial > 200: #cas d'une réduction de 5%
prix=prix_initial*0.95 # 0.95 correspond à 1-5/100
elif prix_initial > 50: # cas d'une réduction de 2%
prix=prix_initial*0.98 # 0.98 correspond à 1-2/100
else: # cas sans réduction
prix=prix_initial
return prix
-
def engager(prix_initial):
# prix à l'issue d'éventuelles réductions :
prix = promotion(prix_initial)
# demande du choix de client :
choix = input("Voulez payer 1% de plus, argent qui sera renversé à une association humanitaire ou écologique. Répondre OUI ou NON.")
if choix == "OUI":
prix = prix*(1+1/100) # augmentation de 1%
return prix