Avant -propos
Cette page sert à acquérir les méthodes pour travailler avec des pourcentages de proportion et des pourcentages d'évolution.
Cette page contient :
-
Un cours en format imprimable
téléchargeable ici qui reprend le cours de cette page Web,
-
Des vidéos expliquant les éléments du cours,
-
Des exercices d'application directs du code dont la correction peut être obtenue grâce à un code de déblocage,
-
Un lien vers les exercices du livre.
Pourcentage : expression d’une proportion
Population et sous-population
Chez un concessionnaire vendant des voitures :
Une entreprise pharmaceutique produit des médicaments. Ce laboratoire est spécialisé dans la fabrication
d’antipyrétique (=contre la fièvre), d’antibiotiques et de vaccins.
L’entreprise veut effectuer une étude sur l’ensemble des médicaments produits.
-
Citer la population étudiée.
-
Citer deux sous-populations.
Proportion d’une sous-population
Soient $E$ une population ayant $n_E$ individus et $A$ une population de $E$ ayant $n_A$ individus.
-
La proportion de $A$ par rapport à $E$ est le quotient :
$\displaystyle{p_A=\frac{n_A}{n_E} =\frac{\text{Nombre d’individus de $A$}}{\text{Nombre d’individus de $E$}}}$.
-
La pourcentage de $A$ par rapport à $E$ est :
$\displaystyle{p_A \times 100=\frac{n_A}{n_E} \times 100=\frac{\text{Nombre d’individus de $A$}}{\text{Nombre d’individus de $E$}}\times 100}$.
Une proportion est toujours comprise entre 0 et 1.
Une proportion de $\dfrac{3}{5}$, c'est-à-dire de $0.60$ correspond à $60$%.
Voici le répartition des élèves d’une classe suivant le genre, la LV1 et le régime de demi-pension :

-
Quelle est la proportion des garçons parmi les externes ?
-
Quel est de pourcentage des élèves faisant allemand ?
-
-
Quel est la proportion de demi-pensionnaire dans la classe ?
-
Parmi les demi-pensionnaires, quelle est la proportion de filles ?
-
Quelle est la proportion de filles demi-pensionnaires dans la classe ?
-
Comment peut-on trouver la proportion précédente à l'aide des proportions trouvées aux questions a. et b. ?
Savoir calculer le pourcentage d’une valeur
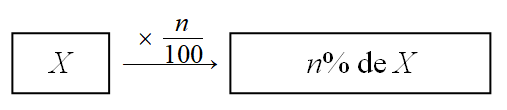
Prendre $n$% d’une grandeur $X$ revient à la multiplier par $\dfrac{n}{100}$.
Savoir calculer la proportion d’une proportion :
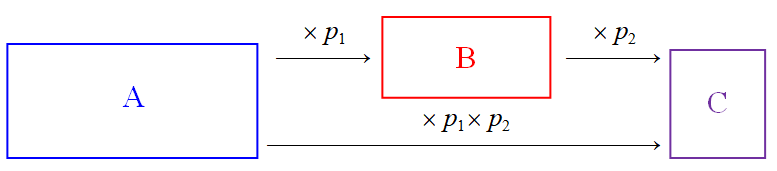
On considère une population $A$, une sous-population $B$ de $A$ et une sous-population $C$ de $B$.
On note $p_1$ la proportion de la sous-population $B$ dans $A$.
On note $p_2$ la proportion de la sous-population $C$ dans $B$.

La proportion de la sous-population $C$ dans $A$ est donnée par $p_1 \times p_2$.
(Source INSEE : https://www.insee.fr/fr/statistiques/2418126).
D’après une projection de l’INSEE , la France métropolitaine comptera 71,63 millions d’habitants en 2050.
Les personnes âgées de 65 ans et plus représenteraient 27.3% de la population totale tandis que les femmes représenteraient 54.2% des personnes d’au moins 65 ans.

Déterminer le pourcentage de femmes d’au moins 65 ans dans la population totale projetée en 2050.
Méthode : travailler uniquement avec des proportions !
-
L’addition de deux pourcentages n’a de sens que lorsque ces pourcentages portent sur des parties d’un
même ensemble de référence n’ayant pas d’éléments communs.
-
Lorsque deux pourcentages portent sur des ensembles de référence distincts, leur ordre ne
renseigne pas sur l’ordre des données absolues.
Variations d’une quantité
Considérons une quantité passant de la valeur initiale $V_i$ à la valeur finale $V_f$.
-
La variation absolue est la différence $\text{valeur finale – valeur initiale}$, soit $V_f − V_i$.
-
La variation relative (appelé aussi taux d’évolution) est le quotient :
$\dfrac{\text{valeur finale – valeur initiale}}{\text{valeur initiale}}$, soit $\dfrac{V_f − V_i}{V_i}$.
Compléter le schéma suivant à l'aide des définitions ci-dessus :

Considérons une quantité passant de la valeur initiale $V_i$ à la valeur finale $V_f$.
-
Le pourcentage d'évolution est le taux d’évolution (=variation relative) exprimé en pourcentage. D’où :
$\text{pourcentage d'évolution}=\text{variation relative}\times 100
=\dfrac{\text{valeur finale−valeur initiale}}{\text{valeur initiale}}\times 100=\dfrac{V_f−V_i}{V_i}\times100$.
-
Le coefficient multiplicateur est le rapport $CM=\dfrac{\text{valeur finale}}{\text{valeur initiale}}$, soit
$CM=\dfrac{V_f}{V_i}$.
La population en France métropolitaine au 1er janvier 2020 était d’environ 64.90 millions.
(source INSEE : https://www.insee.fr/fr/statistiques/1892088?sommaire=1912926.)
L’INSEE prévoit une population en France métropolitaine au 1er janvier 2050 de 71.63 millions.
(Source INSEE : https://www.insee.fr/fr/statistiques/2418126.)
-
-
Estimer la variation absolue de la population française métropolitaine entre 2020 et 2050.
-
Interpréter concrètement cette variation absolue.
-
-
Estimer la variation relative de la population française métropolitaine entre 2020 et 2050.
-
En déduire le pourcentage d’évolution de la population française métropolitaine entre 2020 et 2050.
-
-
Estimer le coefficient multiplicateur correspondant à l’évolution de la population française métropolitaine entre 2020 et 2050.
-
Quelle relation pouvez-vous conjecturer entre la variation relative et le coefficient multiplicateur ?
Évolution d’une quantité
Augmentation, diminution
-
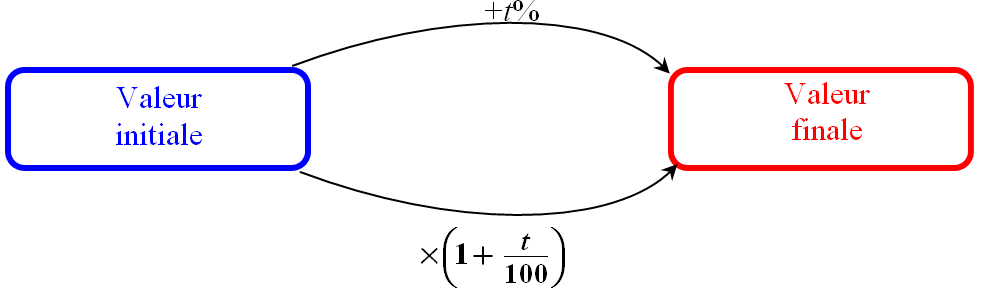
Augmenter une grandeur de $t$% équivaut à multiplier sa valeur initiale par $\left(1+ \dfrac{t}{100}\right)$ .
-
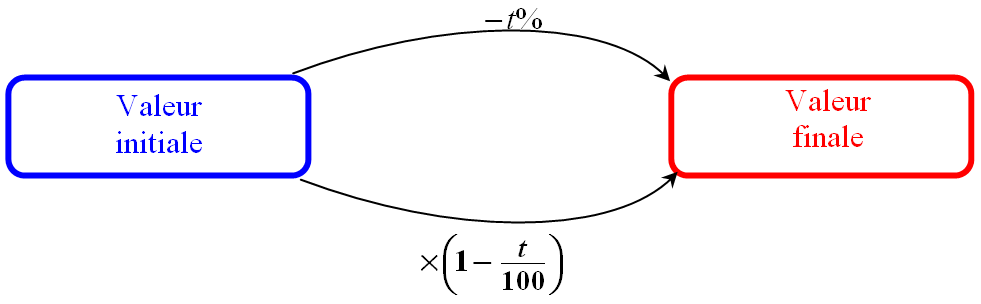
Diminuer une grandeur de $t$% équivaut à multiplier sa valeur initiale par $\left(1- \dfrac{t}{100}\right)$ .
Vous êtes salarié.e.s d’une entreprise. Votre rémunération mensuelle brute s’élève à 1500€.
L’entreprise vous propose une augmentation de 5%.
Quel sera le montant de votre rémunération mensuelle brute après cette augmentation ?
Méthode : faire un schéma et utiliser le coefficient multiplicateur correspondant à l’évolution
Évolutions successives
Pour appliquer plusieurs évolutions successives, il suffit de multiplier la quantité par le produit
des coefficients multiplicateurs de chaque évolution.
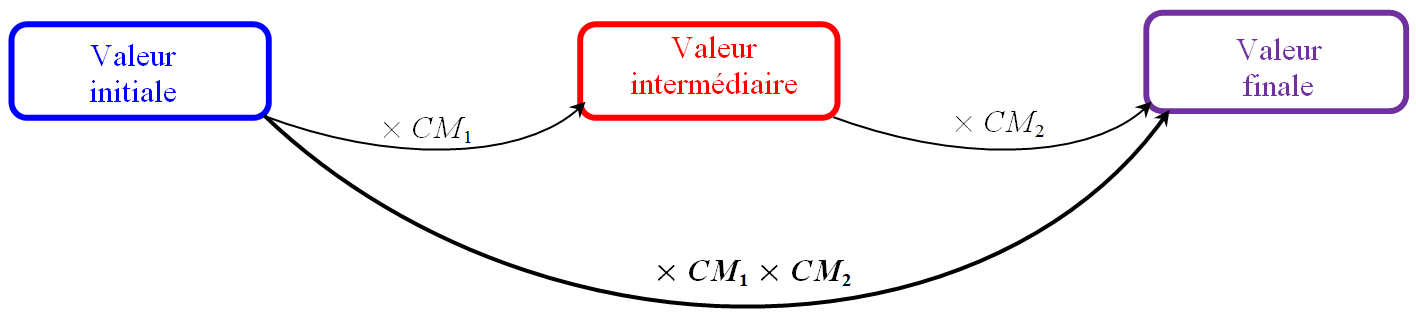
Un article coûtant 20€ en janvier a augmenté de 10% en février puis a diminué de 10% en mars.
-
Quel est le prix de l’article fin mars ?
Méthode : faire un schéma et utiliser le coefficient multiplicateur correspondant à l’évolution
-
Quel est le pourcentage d’évolution du prix de l’article entre janvier et mars ?
En tant que citoyen.ne, il est important de savoir que :
-
Les augmentations et les baisses successives en pourcentages ne s’ajoutent pas, mais les coefficients multiplicateurs se multiplient.
-
Une hausse de t% n’est pas annulée par une baisse de t%.
Évolutions réciproques
On considère une quantité qui évolue d’une valeur initiale $V_i$ à une valeur finale $V_f$.
On appelle taux réciproque le taux d’évolution qui permet de revenir de la valeur finale $V_f$ à celle initiale $V_i$.

Notons $CM$ le coefficient multiplicateur permettant de passer de la valeur initiale $V_i$ à une valeur finale $V_f$ et
$CM_r$ le coefficient multiplicateur réciproque permettant de revenir de la valeur finale $V_f$ à celle initiale $V_i$.
Alors : $CM_r=\dfrac{1}{CM}$.
Ainsi, il suffit de diviser comme l’illustre par le schéma ci-dessous :
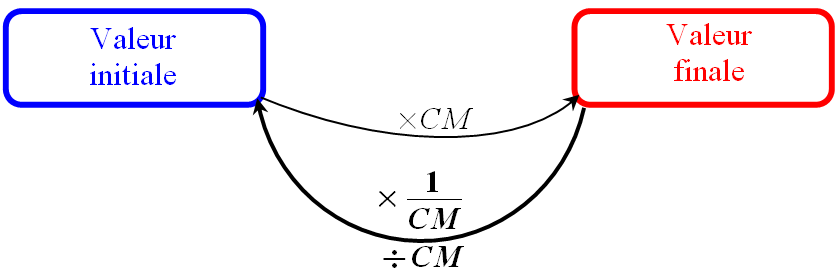
Le cours d’une action a augmenté de 25%.
Calculer le pourcentage d’évolution $t$ qu’il faudrait appliquer pour que l’action revienne à son cours initial.
Exercices
Les exercices du chapitre à faire en autonomie sont ceux du
livre de la classe : le lelivrescolaire