Les phénomènes où apparaît le hasard peuvent être étudiés grâce aux probabilités. La fiabilité d’un objet ou d’un système sont de tels phénomènes.

Vocabulaire sur les probabilités

Deux événements ont un nom particulier :

  1. On appelle l'événement certain un événement qui est toujours réalisé.
    $\Omega$ est un événement certain.

    • "Obtenir un nombre entier entre 1et 6" est un événement certain de l’expérience d’un lancer d’un dé.

    • "Obtenir un nombre entier naturel" est un autre événement certain de l’expérience d’un lancer d’un dé.

  2. Un événement impossible est un événement qui ne se réalise jamais.
    On le note $\emptyset$.

    "Obtenir 4" est un événement impossible de l’expérience d’un lancer de pièce.

L'événement contraire de l’événement $A$, noté $\overline{A}$, est l’événement composé des éventualités qui ne composent pas $A$.

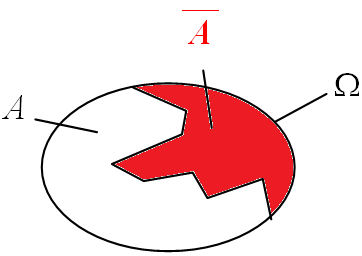
On considère le lancer d'un dé cubique.
Quel est l'événement contraire de l'événement $A=\text{"Obtenir un nombre pair"}$ ?

On appelle événement A et B, l’événement constitué des issues qui appartiennent à $A$ et à $B$ simultanément.
L’événement « $A$ et $B$ » est l’intersection de deux événements : $« A\ et\ B » = A\cap B$.

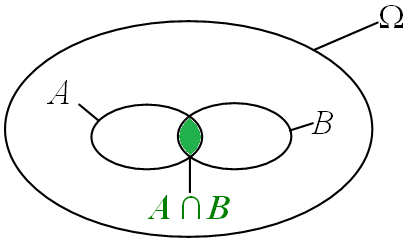
On tire une carte d’un jeu de 32 cartes.
Si l’événement $A$ est "obtenir un as" et $B$ est "obtenir une carte rouge", quel est l’événement $A\cup B$ ?

Deux événements sont dits incompatibles (ou disjoints) lorsque ce sont deux ensembles dont aucune éventualité ne réalise les deux événements : "A et B" est vide.

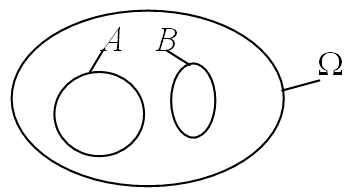
Est-ce que les événements $A$ : "obtenir un nombre strictement inférieur à 3" et $B$ : "Obtenir un nombre multiple de 3" sont incompatibles ? Justifier.

On appelle événement A ou B, l’événement constitué des éventualités qui appartiennent à $A$ ou à $B$.
L’événement « $A$ ou $B$ » est la réunion de deux événements : $« A\ ou\ B » = A\cup B$.

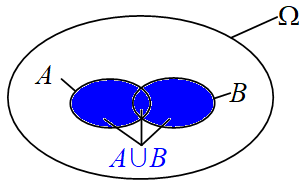
On tire une carte. $A$ est l’événement "Obtenir un trèfle" et $B$ celui "Obtenir un rouge".
Déterminer à l'aide d'une phrase l'événement $A\cup B$.

Propriétés d'une probabilité

Soit $P$ une loi de probabilité sur $\Omega$. Soient $A$ et $B$ deux événements.

La dernière formule peut être comprise, et retenue, ainsi :

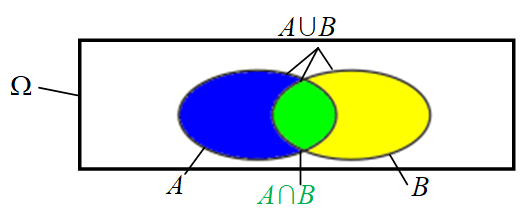
Les éléments de $A\cup B$ sont tous ceux de $A$ auxquels on ajoute tous ceux de $B$.
Or, en faisant ainsi, on compte deux fois l'intersection $A\cap B$ : il faut donc retirer cette intersection une fois.

On considère deux événements $A$ et $B$ tels que $P(A)=0.6$, $P(B)=0.8$ et $P(A\cap B)=0.5$.

  1. Calculer la probabilité $P(\overline{A})$.

  2. Calculer la probabilité $P(A\cup B)$.

Un système est formé de deux amplificateurs A et B qui n’interfèrent pas l’un sur l’autre.
À partir d’un signal appliqué à l’entrée E, on obtient un signal à la sortie si au moins un des deux amplificateurs fonctionne.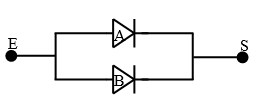
On note respectivement les événements :

On suppose que $P(A)=0.8$, $P(B)=0.9$ et $P(A\cap B)=0.72$.

  1. Calculer la probabilité qu’il y ait un signal à la sortie.

  2. Calculer la probabilité qu’il n'y ait pas un signal à la sortie.

Dans une entreprise informatique de 360 personnes, 25% des salariés ont un diplôme de niveau au plus Bac+2 et 55% des salariés ont un poste à responsabilité. Deux tiers des salariés ayant un diplôme supérieur à Bac+2 ont un poste à responsabilité.

On note $L$ l'événement "avoir un diplôme supérieur à Bac+2" et $R$ l'événement "avoir un poste à responsabilité".

  1. Définir par une phrase l'événement $\overline{L}$.

  2. Définir par une phrase l'événement $\overline{R}\cup L$.

  3. Écrire à l'aide des événements $L$ et $R$ l'événement $A=$"le salairé est un responsable ayant un diplôme de niveau au plus Bac+2".

  4. Calculer le nombre de salariés ayant un diplôme d'au plus Bac+2.

  5. Recopier et compléter le tableau ci-dessous en utilisant des effectifs :

    $L$ $\overline{L}$ Total
    $R$ ... ... ...
    $\overline{R}$ ... ... ...
    Total ... ... ...

  6. Calculer la probabilité $P(\overline{L})$ de deux manières différentes.

  7. Calculer le probabilité de $\overline{R}\cap L$.

  8. En déduire le probabilité de $\overline{R}\cup L$.

  9. Déterminer la probabilité qu'une salarié ayant un diplôme d'au plus Bac+2 ait un poste à responsabilité.

Probabilité conditionnelle

Exemple introductif

Dans un lot de 32 produits fabriqués par une entreprise, 8 ont subi un contrôle A, 12 le contrôle B et 3 les deux contrôles.
On prend un produit ayant subi le contrôle A. Le but est de calculer la probabilité qu’il ait subi aussi le contrôle B ?
On note $A$ l'événement "le produit a subi le contrôle A" et $B$ l'événement "le produit a subi le contrôle B".

  1. Reproduire et compléter le tableau suivant avec des effectifs :

    $A$ $\overline{A}$ ...
    $B$ ... ... ...
    $\overline{B}$ ... ... ...
    ... ... ... ...

  2. On prend un produit ayant subi le contrôle A. Quelle est la probabilité qu’il ait subi aussi le contrôle B ?

  3. Deviner une formule liant la probabilité cherchée avec deux probabilités liées aux événements $A$ et $B$.

Conditionnement par un événement

Soit $P$ une probabilité sur un univers fini $\Omega$. On considère $A$ et $B$ deux événements de $\Omega$, A étant de probabilité non nulle.
On appelle probabilité de B sachant A, le réel noté $P_A(B)$, qui correspond àla probabilité que l'événement $B$ soit réalisé dans le cas où l'événement $A$ est réalisé.

Une probabilité condionnelle est utilisée lorsque l'ensemble de référence n'est plus l'univers $\Omega$ mais un événement $A$.

Parmi les phrases suivantes, repérer celles qui définissent une probabilité conditionnelle :

  1. 35% des individus de cette population sont bilingues.

  2. Parmi les anglicistes de cette population, 20% sont trilingues.

  3. 20% de cette population parle anglais et allemand.

  4. Cette population est composée d'individus de neuf nationalités différentes.

  5. 50% des européens de cette population sont bilingues.

Formule à connaître par coeur :

Si $A$ et $B$ sont tous deux de probabilité non nulle, alors les probabilités conditionnelles $P_A(B)$ et $P_B(A)$ sont toutes les deux définies et on a :
$ P_A(B)=\dfrac{P(A\cap B)}{P(A)}$ et $ P_B(A)=\dfrac{P(A\cap B)}{P(B)}$

On considère une loterie, dont certains tickets sont gagnants.
Dans cette loterie, il y a des tickets rouges et d'autres tickets. On tire au hasard un ticket de loterie.
On appelle $R$ l'événement "le ticket tiré est rouge" et "G" l'événement "le ticket tiré est gagnant".
Traduire en termes de probabilités les phrases suivantes.

  1. Le quart des tickets rouges sont gagnants.

  2. Le tiers des tickets gagnants sont rouges.

  3. Un ticket sur cinq est rouge et gagnant.

  4. Un ticket perdant sur cinq est rouge.

$A$ et $B$ sont deux événements.

  1. Soit $P_A(B)=0.6$ et $P(A\cap B)=0.3$. Calculer $P(A)$.

  2. Soit $P(B)=0.7$ et $P_B(A)=0.2$. Calculer $P(A\cap B)$.

$A$ et $B$ sont deux événements tels que $P(A)=0.2$, $P(B)=0.1$ et $P(A\cap B)=0.05$.

  1. Calculer $P_B(A)$.

  2. Calculer $P_A(B)$.

  3. Calculer $P(A\cup B)$.

  4. Calculer $P(\overline{A}\cap B)$.

Une épidémie de grippe touche le quart de la population.
Le tiers de la population a été vacciné contre la grippe et on estime qu’un malade grippé sur 10 est vacciné.
On note $G$, l’événement "la personne est grippée" et $V$ l’événement "la personne a été vaccinée".

  1. Traduire les donnés de l’énoncé en terme de probabilités (conditionnelles ou pas) faisant intervenir les événements $G$ et $V$.

  2. Calculer la probabilité pour un individu vacciné de cette population d’être malgré tout grippé.

Une entreprise fabrique des pièces métalliques, qui peuvent présenter deux types de défauts : un défaut de longueur $L$ et un défaut de surface $S$.
On a estimé que dans un lot de pièces, la probabilité de choisir une pièce présentant le défaut $L$ est estimée à 0,02, tandis que 8% des pièces présentent le défaut $S$. Enfin, 0,16% des pièces produites le sont avec les deux défauts.

  1. Déterminer la probabilité de pièces ne présentant pas le défaut $L$.

  2. Déterminer la probabilité de pièces présentant au moins un des défauts.

  3. Déterminer la probabilité de pièces ne présentant aucun défaut.

  4. On choisit une pièce au hasard n'ayant pas le défaut $S$. Quelle est la probabilité qu'elle ne présente aucun défaut ?

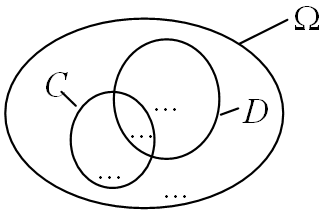
Dans un restaurant, on a constaté que :

On note $C$ l'événement : "le client prend un café" et $D$ celui : "le client prend un dessert".

  1. Reproduire et compléter le diagramme de Venn suivant avec des probabilités :

  2. On choisit un client du restaurant au hasard. Quelle est la probabilité qu'il prenne un dessert et un café ?

  3. Quelle est la probabilité que ce client pris au hasard ne prenne ni dessert ni café ?

  4. On choisit un client ayant pris un café. Quelle est la probabilité qu'il n'ait pas pris de dessert ?

  5. Sachant qu'un client n'a pas pris de café, quelle est la probabilité qu'il n'ait pas pris de dessert ?

Événements indépendants

Soit $P$ une probabilité sur l'univers $\Omega$.
Deux événements $A$ et $B$ sont dits indépendants si $P(A\cap B)=P(A)\times P(B)$.

Voici une définition équivalente dans le cas où $A$ et $B$ sont de probabilités non nulles :

Deux événements $A$ et $B$, de probabilité non nulle, sont indépendants s'ils vérifient l'une des deux conditions suivantes : $P_A(B)=P(B)$ ou $P_B(A)=P(A)$.

$P_A(B)=P(B)$ signifie que la probabilité que l'événement $B$ soit réalisé ne dépend pas du fait que $A$ soit réalisé ($P_A(B)$) ou pas.

On tire une boule dans une urne qui contient 10 boules numérotées de 1 à 10.
On note $A$ l'événement "la boule tirée a un numéro impair" et $B$ l’événement "la boule tirée a un numéro supérieur strictement à 6".

  1. Calculer $P(A)$ et $P(B)$.

  2. Les événements $A$ et $B$ sont-ils incompatibles ?

  3. Les événements $A$ et $B$ sont-ils indépendants ?

Ne pas confondre événements indépendants et événements incompatibles !

Soient deux événements $A$ et $B$ vérifiant : $P(A)=0.4$ ; $P(B)=0.3$ et $P(A\cup B)=0.58$.
$A$ et $B$ sont-ils indépendants ?

On a truqué un dé de sorte que les probabilités d'apparition de chaque face lors d'un lancer soient données par le tableau ci-dessous :

Numéro 1 2 3 4 5 6
Probabilité 0.40 0.15 0.15 0.05 $\ x\ $ $\ y\ $

  1. Déterminer $x$ et $y$ sachant que la probabilité d'apparition du 5 est le quadruple de celle du 6.

  2. Calculer la probabilité d'apparition d'un numéro impair.

  3. Calculer la probabilité d'apparition du 1 sachant que le numéro sorti est impair.

  4. On considère les événements suivants : $A$ : "le résultat est pair", $B$ : "le résultat est multiple de 3" et $C$ : "le résultat est inférieur ou égal à 3".

    1. $A$ et $B$ sont-ils indépendants ?

    2. $A$ et $C$ sont-ils indépendants ?

Arbre de probabilité

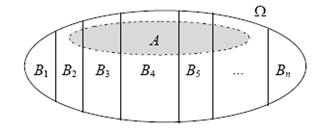
Soit $\Omega$ un univers associé à une expérience aléatoire et $n$ un entier naturel supérieur ou égal à 2. On dit que les événements $B_1$, $B_2$, …, $B_n$ forment une partition de l’univers $\Omega$ si :

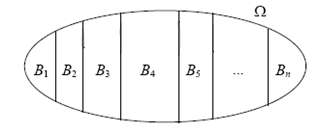
On considère l'ensemble des élèves et étudiants d'un lycée comme le vôtre.

Proposer deux partitions différentes possibles de cet ensemble de personnes.

Soit $B_1$, $B_2$, …, $B_n$ des événements de probabilités non nulles formant une partition de l'univers $\Omega$.
Pour tout événement $A$, $P(A)=P_{B_1}(A)\times P(B_1)+P_{B_2}(A)\times P(B_2)+…+P_{B_n}(A)\times P(B_n)$.
Cette égalité s'appelle la formule des probabilités totales.

Pour utiliser cette formule, vous construirez d'abord un un arbre de probabilité :

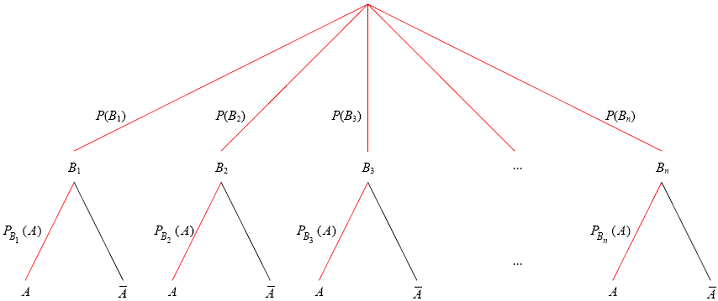
Dans cet arbre, vous aurez à respecter les règles suivantes :

Règles de construction :

  1. L'intersection de deux événements ($B_k \cap A$) est assimilé au chemin $--- B_k ---A$.

  2. Tous les chemins qui partent d'un événement (aux nœuds) constituent une partition de cet événement.

  3. Sur la première branche du chemin est placée la probabilité ($P(B_k)$) et sur la seconde des probabilités conditionnelles ($P_{B_k}(A)$).

Règles de calcul :

  1. La somme des probabilités des branches issues d'un même nœud est 1. (car les $B_k$ forment une partition),

  2. La probabilité de l'événement correspondant à un chemin est le produit des probabilités des branches composant ce chemin.
    (exemple : Chemin $---B_2 ---A$ : $P(B_2 \cap A)=P_{B_2}(A)\times P(B_2)$ d'après formule des probabilités conditionnelles)

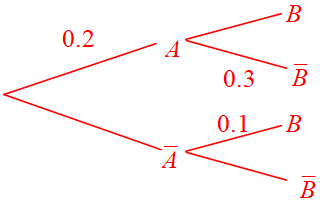
$A$ et $B$ sont deux événements relatifs à une expérience représentée par l'arbre suivant :

  1. Reproduire et compléter l'arbre de probabilité donné.

  2. Calculer la probabilité $P(A\cap B)$.

  3. Calculer la probabilité $P(\overline{A}\cap B)$.

  4. Calculer la probabilité $P(B)$.

Un tiroir $T_1$ contient 5 pièces d'or et 5 pièces d'argent. Un tiroir $T_2$ contient 4 pièces d'or et 6 pièces d'argent.
On choisit au hasard l'un de ces tiroirs et dans ce tiroir, on choisit une pièce au hasard.

  1. Représenter cette expérience aléatoire à l'aide d'un arbre de probabilité .

  2. Calculer la probabilité de prendre une pièce d'or.

  3. On extrait une pièce d'or. Calculer la probabilité quelle provienne du tiroir $T_1$.

Un vendeur de matériel informatique se fournit en PC auprès de trois fabricants notés A, B et C. 20% des éléments proviennent du fabricant A, 35% proviennent du fabricant B et le reste provient du fabricant C.

L'asssembleur décide de vendre uniquement les PC d’excellente qualité. Parmi les PC provenant du fabricant A, 5% ne peuvent être vendus car de qualité insuffisante ; parmi ceux provenant du fabricant B, 10% ne peuvent être vendus ; parmi ceux provenant du fabricant C, 20% ne peuvent être vendus.

Un PC est choisi au hasard dans le stock du vendeur de matériel informatique.
On considère les évènements :

  1. Illustrer la situation à l'aide d'un arbre de probabilité .

  2. Calculer la probabilité que le PC provienne du fabricant A et ne puisse être vendu.

  3. Montrer que $P(M)=0.135$.

  4. On sait qu'un PC ne peut être vendu. Quelle est la probabilité qu'il vienne du fabricant B ?

Une usine de montage utilise des roulements à billes provenant de deux entreprises de mécanique de précision, l'une située à Vitry-le-François, l'autre à Nancy. Son stock provient à 40% de l'usine de Vitry-le-François, le reste provenant de Nancy.
De l'usine de Vitry-le-François, on sait que 4,5% de la livraison est inutilisable, car défectueuse.
Quant à Nancy, qui utilise un contrôle de qualité moins poussé, 6% des pièces en provenant sont défectueuses. Enfin, $\dfrac{4}{5}$ des roulements sont peints en rouge dans la production de Vitry-le-François, ce qui ne les empêche pas d'être défectueux dans les mêmes proportions que les autres provenant cette ville. La production nancéen n'est pas peinte.
On prélève un roulement au hasard.

  1. Déterminer la probabilité qu'il soit peint, sachant qu'il provient de Nancy.

  2. Déterminer la probabilité qu'il soit peint.

  3. Déterminer la probabilité qu'il soit conforme, sachant qu'il provient de Nancy.

  4. Déterminer la probabilité qu'il soit conforme, sachant qu'il provient de Vitry-le-François.

  5. Déterminer la probabilité qu'il soit non conforme.

Le chikungunya est une maladie virale transmise d’un être humain à l’autre par les piqûres de moustiques femelles infectées. Un test a été mis au point pour le dépistage de ce virus. Le laboratoire fabriquant ce test fournit les caractéristiques suivantes :

  1. la probabilité qu’une personne atteinte par le virus ait un test positif est de 0,98 ;

  2. la probabilité qu’une personne non atteinte par le virus ait un test positif est de 0,01.

On procède à un test de dépistage systématique dans une population « cible ». Un individu est choisi au hasard dans cette population. On appelle :

  1. $M$ l’évènement : « L’individu choisi est atteint du chikungunya ».

  2. $T$ l’évènement : « Le test de l’individu choisi est positif ».

On note $p$ ($0\le p\le 1$) la proportion de personnes atteintes par la maladie dans la population cible.

  1. Illustrer la situation concrète ghrâce à un arbre de probabilité .

  2. Exprimer $P(M\cup T)$, $P(\overline{M}\cup T)$ puis $P(T)$ en fonction de $p$.

  3. Démontrer que la probabilité de $M$ sachant $T$ est donnée par la fonction $f$ définie sur $[0;1]$ par : $f(p)=\dfrac{98p}{97p+1}$.

  4. On considère que le test est fiable lorsque la probabilité qu’une personne ayant un test positif soit réellement atteinte du chikungunya est supérieure à 0,95.
    En utilisant les résultats de la question précédente, à partir de quelle proportion $p$ de malades dans la population le test est-il fiable ?

Une pièce est usinée successivement par deux machines $M_1$ et $M_2$, les résultats des deux usinages étant indépendants.

Après passage dans la première machine $M_1$, 5% des pièces présentent un défaut.
On note $A$ l’événement : "la pièce est défectueuse après passage dans $M_1$".

Après passage dans la seconde machine $M_2$ (et quel que soit leur état après leur passage dans $M_1$), 2% des pièces présentent un autre défaut.
On note $B$ l’événement : "la pièce est défectueuse après passage dans $M_2$".

On extrait une pièce au hasard parmi les pièces ayant subi les deux usinages.

  1. Déterminer les probabilités de $A$ et de $B$.

    1. Exprimer à l’aide des événements $A$ et $B$ les événements suivants :

      • $C$ : "la pièce est défectueuse pour les deux usinages par $M_1$ et $M_2$",

      • $D$ : "la pièce est défectueuse",

      • $E$ : "la pièce ne présente aucun défaut".

    2. Calculer, sous forme de fraction irréductible, les probabilités des événements $C$, $D$ et $E$.

    1. Sachant que la pièce extraite est défectueuse, quelle est la probabilité que la pièce présente les défauts d’usinage dus aux deux machines ?

    2. Exprimer à l’aide de $A$ et de $B$ l’événement "le défaut provient uniquement de la machine $M_2$", puis sa probabilité.

    3. En déduire la probabilité que le défaut provienne uniquement de la machine $M_2$, sachant que la pièce est défectueuse.

Dans un lot de pièces, on sait que 5% sont défectueuses. La procédure de contrôle des pièces en sortie de fabrication n'est pas parfaite :

On choisit au hasard une pièce en sortie de fabrication. Quelle est la probabilité que :

  1. la pièce soit rejetée ?

  2. la pièce soit saine et acceptée ?

  3. il y ait une erreur de contrôle ?

  4. la pièce soit saine sachant qu'elle est refusée ?

  5. la pièce soit défectueuse sachant qu'elle est acceptée ?

En France, les statistiques font apparaître que parmi les adultes environ 4% des hommes et 5% des femmes sont asthmatiques.
Dans la population, on considère l'ensemble des couples homme-femme.
Dans cet exercice, les résultats seront arrondis, si nécessaire, à $10^{-3}$ près.

Partie A : Étude de l'état d'asthme du couple

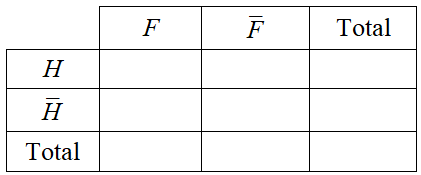
On choisit un couple au hasard. On note $H$ l'événement "l'homme est asthmatique" et $F$ "la femme est asthmatique".
On admet que les événements $F$ et $H$ sont indépendants.

  1. Reproduire et compléter le tableau de probabilités suivant :

  2. En déduire la probabilité des événements suivants :

    1. $A$ : "Aucun n'est asthmatique".

    2. $B$ : "Un seul est asthmatique".

    3. $C$ : "Les deux sont asthmatiques".

    3. Partie B : Étude de la transmission de l'asthme au premier enfant

    Les études actuelles montrent que :

    • si aucun des deux parents n'est asthmatique, la probabilité que leur enfant soit asthmatique est 0.1 ;

    • si un seul des deux parents est asthmatique, la probabilité que leur enfant soit asthmatique est 0.3 ;

    • si les deux parents sont asthmatiques, la probabilité que leur enfant soit asthmatique est 0.5.

    On note $E$ l'événement : "le premier enfant du couple est asthmatique".

    1. Construire un arbre illustrant cette situation concrète.

    2. Calculer $P(E)$.

    3. Calculer les probabilités conditionnelles $P_E(A)$ et $P_E(\overline{A})$. Interpréter ces probabilités.

    4. Quelle est la probabilité qu'un enfant non asthmatique ait au moins l'un de ses deux parents asthmatiques ?

On étudie un modèle de propagation d’un virus dans une population, semaine après semaine. Chaque individu de la population peut être, à l’exclusion de toute autre possibilité :

Un individu est immunisé lorsqu’il a été vacciné, ou lorsqu’il a guéri après avoir été atteint par le virus.
Pour tout entier naturel $n$, le modèle de propagation du virus est défini par les règles suivantes :

On choisit au hasard un individu dans la population. On considère les évènements suivants :

En semaine 0, tous les individus sont « de type S ».

  1. Donner les probabilités $P(S_0)$, $P(M_0)$ et $P(I_0)$.

  2. Reproduire et compléter l’arbre de probabilité suivant :

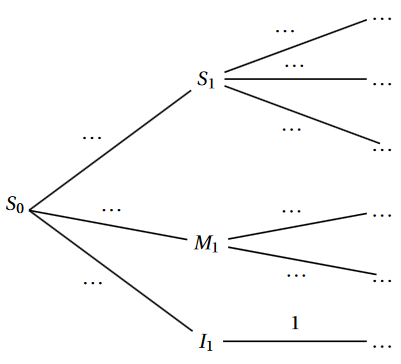
  3. Montrer que $P(I_2)=0.2025$.

  4. Sachant qu’un individu est immunisé en semaine 2, quelle est la probabilité, arrondie au millième, qu’il ait été malade en semaine 1 ?

Dans un atelier, deux machines $M1$ et $M2$ découpent des pièces métalliques identiques. $M1$ fournit 60% de la production (parmi lesquelles 6,3% sont défectueuses), le reste étant fourni par $M2$ (dont 4% de la production est défectueuse).
La production du jour est constituée des pièces produites par les deux machines, et on en tire enfin de soirée une pièce au hasard (tous les prélèvements sont supposés équiprobables).

Partie A. Utilisation des formules des probabilités conditionnelles

  1. Quelle est la probabilité de prélever une pièce défectueuse, sachant qu'elle est produite par $M1$ ?

  2. Quelle est la probabilité de prélever une pièce défectueuse, sachant qu'elle est produite par $M2$ ?

  3. Quelle est la probabilité de prélever une pièce défectueuse ?

Partie B. Utilisation d'un tableau

  1. On suppose maintenant que la production est composée de $x$ pièces.

    1. Reproduire et compléter le tableau suivant :

    2. Quelle est la probabilité de prélever une pièce défectueuse, sachant qu'elle est produite par $M1$ ?

    3. Quelle est la probabilité de prélever une pièce défectueuse, sachant qu'elle est produite par $M2$ ?

    4. Quelle est la probabilité de prélever une pièce défectueuse ?

  2. Quelle conclusion tirer des parties A et B ?

Partie C. Utilisation d'un arbre de probabilité

  1. Dresser un arbre des probabilités conditionnelles relatif à la situation proposée.

    1. Quelle est la probabilité de prélever une pièce défectueuse, sachant qu'elle est produite par $M1$ ?

    2. Quelle est la probabilité de prélever une pièce défectueuse, sachant qu'elle est produite par $M2$ ?

    3. Quelle est la probabilité de prélever une pièce défectueuse ?

  3. Quelle conclusion tirer des parties A, B et C ?

Un institut effectue un sondage pour connaître, dans une population donnée, la proportion de personnes qui sont favorables à un projet d’aménagement du territoire.

Parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu’elles sont favorables au projet. L’institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d’entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable.
Ainsi, une personne qui se dit favorable peut :

  1. soit être en réalité favorable au projet si elle est sincère.

  2. soit être en réalité défavorable au projet si elle n’est pas sincère.

Par expérience, l’institut estime à 15 % le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l’opinion de la personne interrogée.

Le but est, à partir des données recueillies, de déterminer le taux réel de personnes favorables au projet, à l’aide d’un modèle probabiliste. On prélève au hasard la fiche d’une personne ayant répondu, et on définit :

  1. D'après les données recueillies et l'expérience de l'institut de sondage, quelle est la valeur de chacune des probabilités suivantes :

    1. $P(A)$ ?

    2. $P_F(A)$ ?

    3. $P_{\overline{F}}(A)$ ?

  2. On pose $x=P(F)$.

    Illustrer le problème concret à l'aide d'un arbre de probabilité .

  3. Utiliser l'arbre précédent pour obtenir une équation dans laquelle $x$ apparaît.

  4. Déterminer, parmi les personnes ayant répondu au sondage, la proportion de celles qui sont réellement favorables au projet.

Demander le programme !

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲