Nous allons étudier dans ce chapitre la notion de dérivation.
Cette notion est une notion fondamentale en analyse. Elle est très utile pour étudier le comportement global de phénomènes continus comme des signaux électriques par exemple, trouver des valeurs correspondant à des contraintes physiques données, ...

La notion de dérivation a été développée à partir du XVIIè siècle suite aux travaux indépendants d' Isaac Newton et de Gottfried Leibniz, même si des prémices du calcul infinitésimal sont étudiés dès l'antiquité avec Archimède.

Dans tout ce chapitre, $f$ est une fonction définie sur un intervalle $I$ dont la courbe représentative est notée $\mathcal{C}_f$ dans un repère orthogonal. $a$ désigne un réel quelconque de l'intervalle $I$.

Nombre dérivé

On veut étudier l'évolution l'altitude d'un cycliste le long d'un parcours de 60 km.
Pour simplifier, on suppose que le profil du parcours est donnée par la fonction $h$ dont la courbe est donnée ci-dessous.

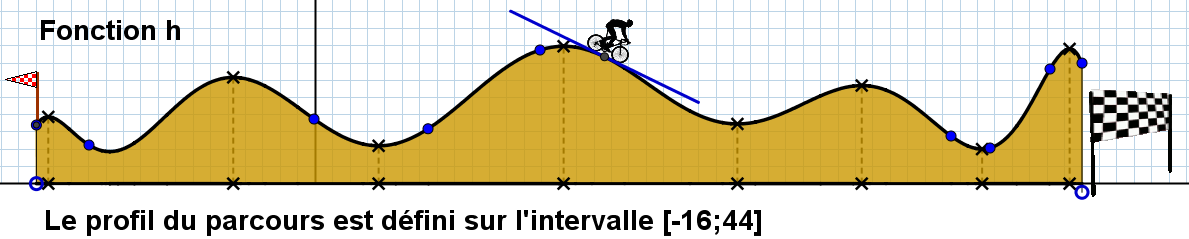
L'évolution de l'altitude de la pente va dépendre de la pente à chaque endroit du parcours.
Cette pente est donnée par la droite collant le plus possible au profil du parcours : cette droite est appelée la tangente.

La pente de cette droite est donnée par le coefficient directeur de cette droite, nombre obtenu comme le rapport entre l'accroissement vertical sur l'accroissement horizontal.

Par exemple, peu après le départ, le cycliste descend une pente raide :
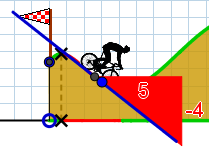
L'endroit où il se trouve la pente est telle qu'avancer horizontalement de 5 revient à descendre de 4.
La pente à cet endroit est donc défini par le rapport $\dfrac{-4}{-5}$, soit le nombre $-\dfrac{4}{5}$.
Comme le cycliste se trouve alors à l'endroit repéré par l'abscisse $-13.5$, on note cette pente : $h'(-13.5)=-\dfrac{4}{5}$.

Déterminer la pente du parcours à chacune des positions suivantes en concluant, comme dans l'exemple précédent, en utilisant la notation $h'(...)=...$ :

  1. Le cycliste est à l'endroit repéré par l'abscisse $-4$ :
    Ici, $h'(-4)=...$

  2. Le cycliste est à l'endroit repéré par l'abscisse $5$ :
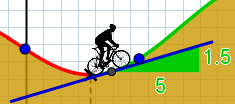
    Ici, $h'(5)=...$

  3. Le cycliste est à l'endroit repéré par l'abscisse $13$ :

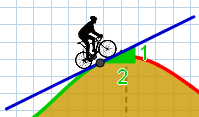
  4. Le cycliste est à l'endroit repéré par l'abscisse $14$ :

  5. Le cycliste est à l'endroit repéré par l'abscisse $15$ :

  6. Le cycliste est à l'endroit repéré par l'abscisse $32$ :

On suppose que $\mathcal{C}_f$ admet au point $A$ d'abscisse $a$ une tangente $\mathcal{T}$ non parallèle à l'axe verticale.
On dit alors que $f$ est dérivable en $a$.
Le coefficient directeur de cette tangente en $\color{red}{A(a;f(a))}$ est alors appelé nombre dérivé de $f$ en $a$ et est noté $f'(a)$.

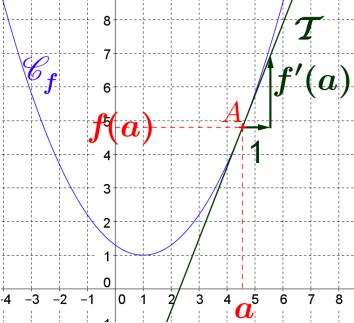
Soit $\mathcal{T}$ la tangente (non horizontale) à $\mathcal{C}_f$ admet au point $A$ d'abscisse $a$.

$\mathcal{T}$ a pour équation $y=f'(a)×(x−a)+f(a)$.
$\mathcal{T}$ a pour coefficient directeur $f'(a)$ et passe par le point $A(a;f(a))$.

L'équation de la tangente au point d'abscisse $a$ est à connaître par coeur !

Ci-dessous est tracée la courbe représentant une fonction $f$ ainsi que quelques unes de ses tangentes.

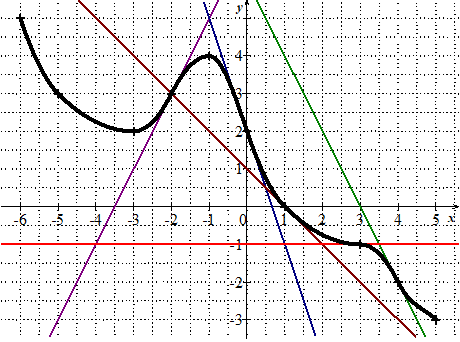
  1. Lire graphiquement $f(-2)$.

  2. Lire graphiquement $f'(-2)$.

    • une image se lit sur l'axe des ordonnées,

    • un nombre dérivé se lit comme pente de la tangente.

  3. Déterminer l'équation de la tangente au point d'abscisse $-2$.

    Utiliser la formule de cours ci-dessus.

  4. Lire $f(3)$.

  5. Lire $f'(3)$.

  6. Déterminer l'équation de la tangente au point d'abscisse $3$. Est-ce cohérent avec le graphique ?

  7. Lire $f(4)$.

  8. Lire $f'(4)$.

  9. Lire $f'(0)$.

  10. Déterminer graphiquement une valeur approchée de $f'(-3)$.

  11. Déterminer graphiquement une valeur approchée de $f'(-5)$.

La courbe $\mathcal{C}$ donnée dans la figure ci-dessous représente une fonction $f$ définie et dérivable sur l’intervalle $[-1;5]$. Cette courbe est tracée dans un repère orthonormal.
On a représenté les tangentes $T_0$, $T_1$, $T_3$ et $T_5$ aux points de $\mathcal{C}$ d’abscisses respectives 0, 1, 3 et 5.
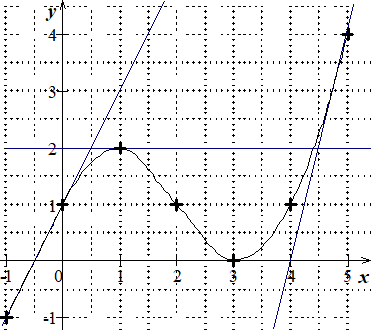
Par lecture graphique :

  1. Déterminer les valeurs de $f(0)$, $f(1)$, $f(3)$ et $f(5)$.

  2. Déterminer les valeurs de $f'(0)$, $f'(1)$, $f'(3)$ et $'f(5)$.

  3. Déterminer l’équation de chaque tangente $T_0$, $T_1$, $T_3$ et $T_5$.

Soit $f$ la fonction définie par la courbe $\mathcal{C}_f$ ci-dessous.
Certaines de ses tangentes sont tracées.

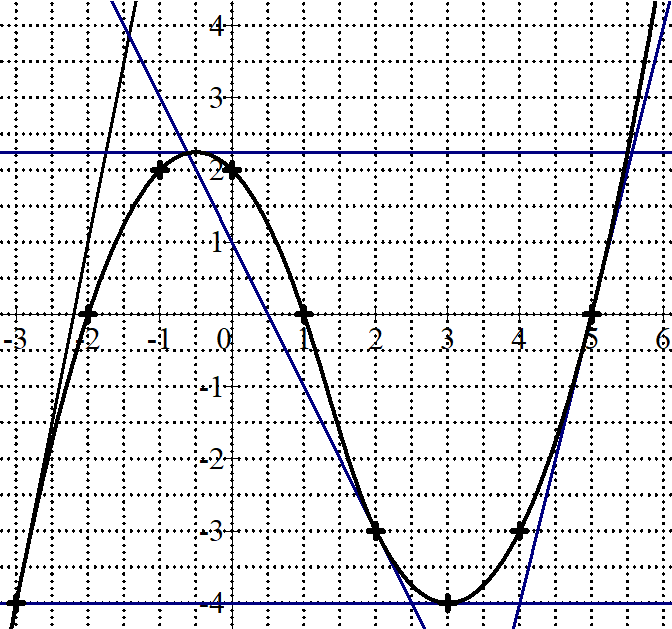
  1. Par lecture graphique, donner la valeur de : $f(2)$, $f'(2)$, $f(5)$ et $f'(5)$.

  2. Est-il vrai que $f'(-3)=-4$ ?

  3. Résoudre graphiquement $f(x)>0$.

  4. Résoudre graphiquement $f'(x)>0$.

  5. Donner une valeur approchée de $f(-0.5)$.

  6. Donner une valeur approchée des solutions de $f(x)=-0.5$.

  7. Lire une valeur approchée de $f'(1)$.

  8. Les tangentes aux points d'abscisses -3 et 5 sont-elles parallèles ?

Fonction dérivée

Définition

Dans plusieurs autres disciplines, en particulier en physique, la dérivée de $t\mapsto f(t)$ est notée $\dfrac{df}{dt}$ au lieu de $f'(t)$.

L'intérêt de cette autre notation réside dans le fait qu'il pourra être écrit que $df=f'(t)dt$ (en multipliant par $dt$ l’égalité $\dfrac{df}{dt}=f'(t)$).

Toutes fonctions construites à l’aide des fonctions polynômes, rationnelles, $\ln$, $exp$, $\sin$ et $\cos$ sont dérivables sur leur ensemble de définition.

Règles de dérivation des fonctions ususelles

Pour dériver une fonction, il est fondmental de connaître par coeur le tableau suivant où apparaissent la dérivée des fonctions usuelles :

Dans ce tableau, $k$ correspond à une constante réelle quelconque et $n$ un réel quelconque :

Fonction $f$ définie par $\mathcal{D}_f$ (ensemble de définition de $f$) Fonction $f'$ définie par $\mathcal{D}_f'$ (ensemble de définition de $f'$)
$f(t)=k$ $\mathbb{R}$ $f'(t)=0$ $\mathbb{R}$
$f(t)=t$ $\mathbb{R}$ $f'(t)=1$ $\mathbb{R}$
$f(t)=at+b$ $\mathbb{R}$ $f'(t)=a$ $\mathbb{R}$
$f(t)=t^n$ $\mathbb{R}$ $f'(t)=nt^{n-1}$ $\mathbb{R}$
$f(t)=\frac{1}{t}$ $]-\infty;0[\cup]0;+\infty[$ $f'(t)=-\frac{1}{t^2}$ $]-\infty;0[\cup]0;+\infty[$
$f(t)=\frac{1}{t^n} (=t^{-n})$ $]-\infty;0[\cup]0;+\infty[$ $f'(t)=-\frac{n}{t^{n+1}} (=-nt^{-n-1})$ $]-\infty;0[\cup]0;+\infty[$
$f(t)=\sqrt{t}$ $[0;+\infty[$ $f'(t)=\frac{1}{2\sqrt{t}}$ $]0;+\infty[$
$f(t)=\sin(t)$ $\mathbb{R}$ $f'(t)=\cos(t)$ $\mathbb{R}$
$f(t)=\cos(t)$ $\mathbb{R}$ $f'(t)=-\sin(t)$ $\mathbb{R}$
$f(t)=e^t$ $\mathbb{R}$ $f'(t)=e^t$ $\mathbb{R}$
$f(t)=\ln(t)$ $]0;+\infty[$ $f'(t)=\frac{1}{t}$ $]0;+\infty[$

Vous pouvez retrouver la formule de dérivation de $t\mapsto \sqrt{t}$ grâce à celle de $t\mapsto t^n$ en sachant que $\sqrt{t}=t^{\frac{1}{2}}$

Utiliser le tableau précédent pour exprimer simplement la dérivée des fonctions usueles suivantes :

  1. $f(t)=t^2$

  2. $g(t)=\dfrac{1}{t^2}$

  3. $h(t)=t^5$

  4. $k(t)=\dfrac{1}{t^5}$


Formules de dérivation

En plus de connaître la dérivée des fonctions usuelles, il est nécessaire de connaître par coeur comment se dérivent certaines opérations et "formes" :

Dans ce tableau, $u$ et $v$ sont deux fonctions dérivables sur $I$, $k$ et $n$ sont des réels ($n$ étant non nul) :

Formules Condition de validité
$(u+v)'=u'+v'$ toujours vrai
$(ku)'=ku'$ toujours vrai
$(uv)'=u'v+uv'$ toujours vrai
$\displaystyle{\left(\dfrac{1}{v}\right)'=-\dfrac{v'}{v^2}}$ $v$ ne s'annule pas sur $I$
$\displaystyle{\left(\dfrac{u}{v}\right)'=\dfrac{u'v-uv'}{v^2}}$ $v$ ne s'annule pas sur $I$
$\displaystyle{\left(\sqrt{u}\right)'=\dfrac{u'}{2\sqrt{u}}}$ $u$ est strictement positive $I$
$\displaystyle{\left(u^n\right)'=n\times u^{n-1}\times u'}$ toujours vrai
$\displaystyle{\left(e^u\right)'=u'\times e^u}$ toujours vrai
$\displaystyle{\left(\ln(u)\right)'=\dfrac{u'}{u}}$ $u$ est strictement positive sur $I$
$\displaystyle{\left(\sin(u)\right)'=u'\times \cos(u)}$ toujours vrai
$\displaystyle{\left(\cos(u)\right)'=-u'\times \sin(u)}$ toujours vrai

Il est essentielle de comprendre qu'une constante liée par une addition deviendra 0 lors de la dérivation, tandis qu'une constante liée par une multiplication est conservée.

Application : dérivation d'une somme

Voici un premier exemple d'utilisation de ce tableau pour dériver une fonction non usuelle.

Considérons la fonction $f:t\mapsto t^3-4t+5$.

Première étape : regarder la forme de la fonction :
$f$ est de la forme $u+v$ avec $u(t)=t^3$ et $v(t)=-4t+5$.

Deuxième étape : dériver chaque élément (plus simple) $u$ et $v$ :
$u$ et $v$ sont des "fonctions usuelles" ; d'après le premier tableau, on a :
$u'(t)=3t^2$ et $v'(t)=-4$

Dernière étape : utiliser la forme de la dérivée proposée dans le dernier tableau :
$f'=u'+v'$ donc $f'(t)=u'(t)+v'(t)$ $=3t^2-4$.

Dériver les fonctions suivantes :

  1. $f:t\mapsto \dfrac{1}{t} + \sqrt{t}$

  2. $g:t\mapsto e^t + \ln(t) -\sin(t)$

  3. $g:t\mapsto \dfrac{1}{t^4} + \cos(t) + \sqrt{2}$

Application : dérivation d'un produit et d'un quotient

Voici un second exemple, à reprendre en cas de blocage lors de la dérivation d'un produit ou d'un quotient :

Soit $f:t\mapsto \dfrac{5t-3}{t^2+1}$.

$f$ est de la forme $\dfrac{u}{v}$ avec $u(t)=2t-3$ et $v(t)=t^2+1$.
$u'(t)=2$ et $v'(t)=2t$.
Comme $\displaystyle{\left(\dfrac{u}{v}\right)'=\dfrac{u'v-uv'}{v^2}}$, $f'(t)=\dfrac{2\times(t^2+1)-(2t-3)\times (2t)}{(t^2+1)^2}$ $=\dfrac{2t^2+2-4t^2+6t}{(t^2+1)^2}$ $=\dfrac{-2t^2+6t+2}{(t^2+1)^2}$

Dériver chacune des fonctions suivantes :

  1. $f(t)=(3-2t)(t^3-t)$

  2. $g(t)=\dfrac{7-3t}{3t+1}$

  3. $h(t)=\dfrac{t}{t^4+t^2+1}$

Justifier que la dérivée de la fonction $f:t\mapsto \sqrt{t}(4t+6)$ est la fonction $t\mapsto \dfrac{6t+3}{\sqrt{t}}$.

Application : dérivation d'une racine carrée

Voici un troisième exemple, à reprendre en cas de blocage lors de la dérivation d'une racine carrée :

Soit $f:t\mapsto 7\sqrt{4t^2+9}$.

$f$ est de la forme $7\sqrt{u}$ avec $u(t)=4t^2+9$.
$u'(t)=4\times 2t$ c'est-à-dire $u'(t)=8t$.
Comme $\displaystyle{\left(\sqrt{u}\right)'=\dfrac{u'}{2\sqrt{u}}}$, $f'(t)=7\times\dfrac{8t}{2\sqrt{4t^2+9}}$ $=7\times\dfrac{4t}{\sqrt{4t^2+9}}$ $=\dfrac{28t}{\sqrt{4t^2+9}}$

Dériver sur $\mathbb{R}$ la fonction $f$ définie par $f(t)=\sqrt{2t^4+t+3}$.

Justifier que la dérivée de la fonction $f$ définie sur $]-1;+\infty[$ par $f(t)=\dfrac{\sqrt{t^2+1}}{t+1}$ est la fonction $t\mapsto \dfrac{t-1}{(t^2+1)^2\sqrt{t^2+1}}$.

Application : dérivation d'une exponentielle

Voici un quatrième exemple, à reprendre en cas de blocage lors de la dérivation d'une exponentielle :

Soit $f:t\mapsto -8 e^{-3t^2+t-1}+4$.

Comme 4 est une constante liée par une addition, elle va disparaître en dérivant ; $f$ peut être vu de la forme $-8 e^u$ avec $u(t)=-3t^2+t-1$.
$u'(t)=-3\times 2t+1$ c'est-à-dire $u'(t)=-6t+1$.
Comme $\displaystyle{\left(e^u\right)'=u' e^u}$, $f'(t)=-8\times(-6t+1)\times e^{-3t^2+t-1}$ $=(48t-8)e^{-3t^2+t-1}$.

Dériver sur $\mathbb{R}$ la fonction $f$ définie par $f(t)=7-9e^{5-2t^2}$.

Justifier que la dérivée de la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=t e^{-t^2}$ est la fonction $t\mapsto (1-2t^2)e^{-t^2}$.

Application : dérivation d'un logarithme népérien

Voici un cinquième exemple, à reprendre en cas de blocage lors de la dérivation d'un logarithme népérien :

Soit $f:t\mapsto -5 \ln(7+3t^2)$.

$f$ est de la forme $-5\ln(u)$ avec $u(t)=7+3t^2$.
$u'(t)=3\times 2t$ c'est-à-dire $u'(t)=6t$.
Comme $\displaystyle{\left(\ln(u)\right)'=\dfrac{u'}{u}}$, $f'(t)=-5\times\dfrac{6t}{7+3t^2}$ $=\dfrac{-30t}{7+3t^2}$.

Dériver sur $]-2;+\infty[$ la fonction $f$ définie par $f(t)=\ln(4+2t)$.

Justifier que la dérivée de la fonction $f$ définie par $\displaystyle{f(t)=2\ln\left(\dfrac{3t+1}{2t+5}\right)}$ est la fonction $t\mapsto \dfrac{26}{(2t+5)(3t+1)}$.

Application : dérivation d'une puissance

Voici un sixième exemple, à reprendre en cas de blocage lors de la dérivation d'une puissance :

Soit $f:t\mapsto 3\times (5-7t^2)^4$.

$f$ est de la forme $3 u^n$ avec $u(t)=5-7t^2$ et $n=4$.
$u'(t)=-7\times 2t$ c'est-à-dire $u'(t)=-14t$.
Comme $\displaystyle{\left(u^n\right)'=n\times u'\times u^{n-1}}$, $f'(t)=3\times 4\times (-14t)\times (5-7t^2)^3$ $=172\times (5-7t^2)^3$.

Dériver sur $\mathbb{R}$ la fonction $f$ définie par $f(t)=2-3(6-t)^5$.

Soit $f$ la fonction définie sur $]1;+\infty[$ par $f(t)=\dfrac{5}{(1-t)^3}$.
En remarquant que $f(t)$ peut s'écrire sous la forme $f(t)=5\times (1-t)^{-3}$, dériver la fonction $f$ sur son ensemble de définition.

Justifier que la dérivée de la fonction $f$ définie par $\displaystyle{f(t)=\dfrac{(t+2)^2}{(3t-2)^3}}$ est la fonction $t\mapsto -\dfrac{(t+2)(3t+22)}{(3t-2)^4}$.

Déterminer les dérivées des fonctions suivantes (éventuellement en recopiant et en complétant les éléments de corrections proposés).

  1. $f(t)=7t-6+\sqrt{6}-\dfrac{1}{t}$

  2. $f(t)=6t^4-8t^3+\pi$

  3. $f(t)=1-\dfrac{t^2}{3}$.

    $\dfrac{t^2}{3}=\dfrac{1}{3}\times t^2$.

  4. $f(t)=\dfrac{4-3t}{2t+1}$.

    Recopier et compléter le texte suivant :
    forme ... avec $u(t)=...$ donc $u'(t)=...$ et $v(t)=...$ donc $v'(t)=...$.
    Ainsi, $f'(t)=...$.

  5. $f(t)=4e^{3-5t}$.

    Recopier et compléter le texte suivant :
    forme ... avec $u(t)=...$ donc $u'(t)=...$.
    Ainsi, $f'(t)=...$.

  6. $f(t)=t \ln(t)$.

    Recopier et compléter le texte suivant :
    forme ... avec $u(t)=...$ donc $u'(t)=...$ et $v(t)=...$ donc $v'(t)=...$.
    Ainsi, $f'(t)=...$.

  7. $f(t)=-2(3-4t)^5$.

    Recopier et compléter le texte suivant :
    forme ... avec $u(t)=...$ donc $u'(t)=...$ et $...$ .
    Ainsi, $f'(t)=...$.

  8. $f(t)=\dfrac{t^2+1}{1-t}$.

    Recopier et compléter le texte suivant :
    forme ... avec $u(t)=...$ donc $u'(t)=...$ et $v(t)=...$ donc $v'(t)=...$.
    Ainsi, $f'(t)=...$.

  9. $f(t)=10\cos\left(2\pi t-\dfrac{\pi}{2}\right)$.

    Recopier et compléter le texte suivant :
    forme ... avec $u(t)=...$ donc $u'(t)=...$.
    Ainsi, $f'(t)=...$.

  10. $f(t)=\dfrac{4}{(2+3t)^7}$.

    Recopier et compléter le texte suivant :
    On peut écrire : $f(t)=\dfrac{4}{(2+3t)^7}=4\times (...)^{...}$.
    forme ... avec $u(t)=...$ donc $u'(t)=...$.
    Ainsi, $f'(t)=...$.

Utilisation de Xcas

Sur Xcas, vous pouvez obtenir la fonction dérivée d'une fonction dérivable grâce à l'instruction deriver(fonction,variable).
Exemple : la dérivée de $f:t\mapsto t e^{-t^2}$ s'obtient avec :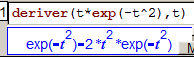

Il est parfois nécessaire d'utiliser en plus de l'instruction deriver les instructions factoriser et simplifier.

Vérifier les dérivées calculées lors de cet exercice précédent.

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(t)=\sin(2t)\times \cos(2t)$.

  1. Déterminer grâce à Xcas la dérivée de la fonction $f$ sur $\mathbb{R}$.

  2. Une fois la fonction $f$ saisie sur Xcas, que renvoie l'instruction factoriser(deriver(f(t),t)) ?

  3. Comparer avec le renvoi de l'instruction factoriser(simplifier(deriver(f(t),t))).
    En quoi cette nouvelle forme obtenue est préférable par etudier $f'(t)$ ?

Déterminer à la main les dérivées des fonctions suivantes puis vérifier le résultat obtenu grâce à Xcas.

  1. $f(t)=\dfrac{4}{3}t^6-\pi t^2+\sqrt{2}-\dfrac{3}{t^2}$.

  2. $f(t)=\dfrac{3t+1}{t^2+t+2}$.

  3. $f(t)=4(5t-2)^3$.

  4. $f(t)=3\ln(t)-\dfrac{5}{t}+4\sqrt{t}$.

  5. $f(t)=3\sqrt{5-4t}$.

  6. $f(t)=4+\ln(t^2+4)$.

  7. $f(t)=\dfrac{5t+3}{t-4}-t$.

  8. $f(t)=-2e^{\frac{1}{t}}$.

  9. $f(t)=1-t-\dfrac{3}{2t+1}$.

  10. $f(t)=3\sin(4t-\pi)$.

Dérivées successives

  1. La dérivée de la fonction $f'$ est appelée dérivée seconde de $f$ et est notée $f''$.

  2. La dérivée de la fonction $f''$ est appelée dérivée troisième de $f$ et est notée $f^{(3)}$.

  3. Plus généralement, pour $n\ge 3$, la dérivée de $f^{(n)}$ est $f^{(n+1)}$.

En physique, vous utiliserez plutôt ces notations :

  1. $\dfrac{df}{dt}$ au lieu de $f'(t)$.

  2. $\dfrac{d^2f}{dt^2}$ au lieu de $f''(t)$.

  3. $\dfrac{d^n f}{dt^n}$ au lieu de $f^{(n)}(t)$.

Interprétation en cinématique :

Un point $M$ est soumis à un mouvement oscillatoire qui, en fonction du temps, est défini par : $x(t)=2\sin\left(4\pi t -\dfrac{\pi}{3}\right)$, où $t$ représente le temps exprimé en seconde et $x(t)$ est en centimètres.

  1. Calculer l'expression, en fonction de $t$, de la vitesse instantanée $x'(t)$ du point $M$.

  2. Calculer l'expression, en fonction de $t$, de l'accélération instantanée $x''(t)$ du point $M$.

Code de déblocage de la correction :

Utilisation de la dérivation

Étude de variations

Soit $f$ dérivable sur $I$.

Voici une activité Geogebra pour illustrer ce théorème.
Glisser le curseur Mouvement afin de déplacer le cycliste et observer le lien entre variations de $h$ et signe de sa dérivée $h'$ :

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(t)=e^{-t}(t^3−t^2−t+5)$.

  1. Quel code saisir sur Xcas pour obtenir l'expression $f'(t)$ de la dérivée de $f$ sur $\mathbb{R}$ ?

  2. Comment modifier ce code pour obtenir une forme factorisée de cette dérivée ?

  3. On admet que $f'(t)=(2-t)(t^2-2t-3)e^{-t}$.
    Recopier et compléter le tableau de signe suivant :

    En déduire le tableau de variations de $f$ :

  4. Justifier que pour tout réel $t\ge 2$ : $f(t)\lt 1$.

Code de déblocage de la correction :

La viscosité d'un lubrifiant décroît lorsque la température augmente, mais de façon plus au moins rapide selon sa nature chimique.

Un certain lubrifiant silicone a une viscosité, en $mm^2.s^{-1}$, donnée par $f(t)=-0.7+e^{\frac{1324}{t}}$, où $t$ est la température en Kelvin. (on obtient la température en Kelvin en ajoutant 273 à celle en Celsius).

  1. Justifier que $f$ est bien décroissante sur $]0;+\infty[$.

  2. Déterminer, en degré Celsius, à un degré près, la température à partir de laquelle la viscosité de ce lubrifiant est inférieure à 40 $mm^2.s^{-1}$.

Code de déblocage de la correction :

Extrema locaux d'une fonction

Soient $f$ dérivable sur $I$ et $x_0\in I$.

  1. Si $f$ admet un extremum en $x_0$ alors $f'(x_0)=0$.

  2. Réciproquement, si $f'(x_0)=0$ et si $f'$ change de signe en $x_0$ alors $f(x_0)$ est un extremum local.

Voici un exemple d'utilisation :
trouver le maximum de la fonction $f:t\mapsto \frac{2}{3} t^3-3t^2+4t+1$ sur $[0;2]$.

Étape 1 : Calculer la dérivée de $f:t\mapsto \frac{2}{3} t^3-3t^2+4t+1$ sur $\mathbb{R}$ :

$f'(t)=\frac{2}{3}\times 3t^2-3\times 2t+4$ $=2t^2-6t+4$.

Étape 2 : Étudier le signe de cette dérivée sur $\mathbb{R}$ :

La dérivée est un polynîme du second degré avec $a=2$, $b=-6$ et $c=4$.
$\Delta = b^2-4ac=(-6)^2-4\times 2 \times 4=36-32=4$.
$\Delta>0$ : deux racines réelles distinctes.
$x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{6-2}{4}=1$ et $x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{6+2}{2}=2$.
On en déduit le tableau de signe suivant de la dérivée (signe de $a$ à l'extérieur) :

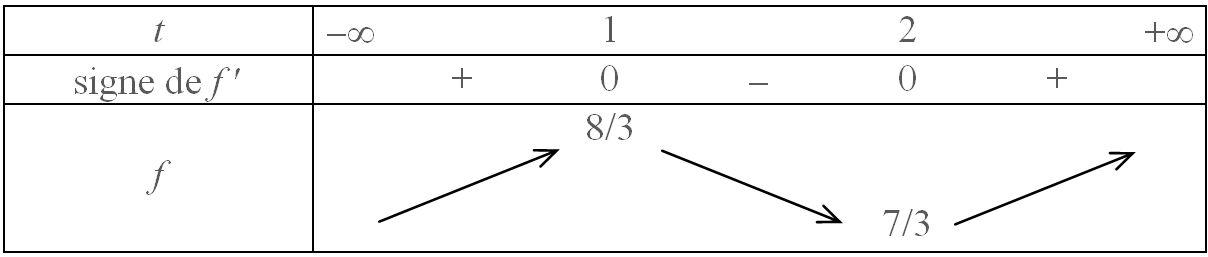
Étape 3 : En déduire les variations de $f:t\mapsto \frac{2}{3} t^3-3t^2+4t+1$ sur $\mathbb{R}$ :

Comme $f(1)=\dfrac{2}{3}+2=\dfrac{8}{3}$ et $f(2)=\dfrac{16}{3}-3=\dfrac{7}{3}$, on peut compléter le tableau précédent en rajoutant une dernière ligne.
On aboutit à ce tableau complet :

Étape 4 : En déduire les variations de $f:t\mapsto \frac{2}{3} t^3-3t^2+4t+1$ sur $[0;2]$ :

En réduisant le tableau précédent à l'intervalle $[0;2]$, on aboutit à ce tableau :

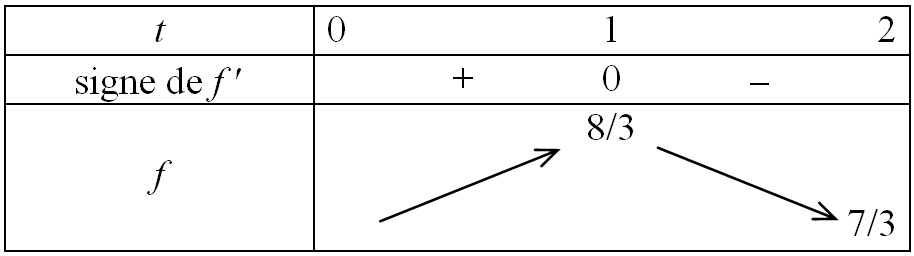
Étape 5 : En déduire le maximum de $f:t\mapsto \frac{2}{3} t^3-3t^2+4t+1$ sur $[0;2]$ :

Le maximum de $f$ sur $[0;2]$ est $\frac{8}{3}$ atteint en $x=1$.

$\frac{8}{3}$ est le maximum de $f$ sur $[0;2]$ mais pas sur $\mathbb{R}$ car, par exemple, $f(3)=4 >\frac{8}{3}$.

Méthode pour obtenir les variations d'une fonction avec Xcas.
Il vous suffira :

  1. de factoriser la dérivée avec factoriser(deriver(fonction,variable))

  2. puis d'étudier le signe de chacun des facteurs avec solve(facteur >0, inconnue)

  3. puis de dresser le tableau de signes de chaque facteur et le tableau de variations de la fonction sur une feuille ; Les démarches effectuées sur Xcas seront vérifiées lors des appels à l'examinateur.

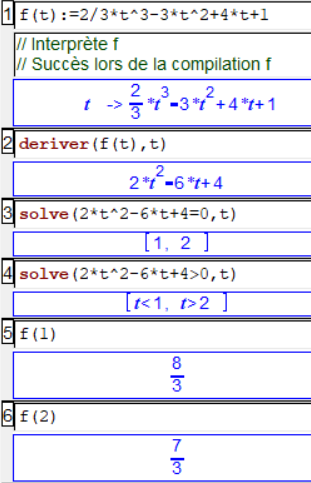
Voici par exemple comment il suffit Xcas pour obtenir le tableau de signes de l'exemple précédent avec Xcas :

  • La réponse de la ligne 3 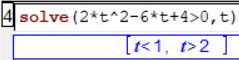permet de d'abord placer les "0" dans le tableau de signes des facteurs de la dérivée :

  • Il faut comprendre la réponse de la ligne 4 comme "$2t^2-6t+4$ est de signe strictement positif lorsque $t$ est strictement plus petit que 1 et aussi lorsque $t$ est strictement plus grand que 2.". On peut ainsi placer les signes "+" dans le tableau de signes au niveau du facteur étudié :

  • Rappel : il est possible d'obtenir une limite avec l'instruction limit(fonction,variable,but).
    Par exemple, si vous vouliez connaître la limite de la fonction $f$ en $+\infty$, il suffirait de rajouter la ligne suivante dans Xcas :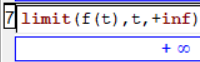

Le but est de montrer que pour tout réel $t>0$ on a : $\sqrt{t} + \dfrac{1}{\sqrt{t}} \ge 2$.

  1. Soit $f:t\mapsto \sqrt{t}+\dfrac{1}{\sqrt{t}}$.
    Montrer que $f'(t)=\dfrac{t-1}{2t\sqrt{t}}$.

    Ne pas hésiter à utiliser Xcas !

  2. Étudier le signe de chacun des facteurs de la dérivée.

  3. En déduire le tableau de variation complet de $f$.

    Ici, les limites aux bornes, c'est-à-dire en 0 et en $+\infty$ sont attendues : ne pas hésiter à utiliser Xcas.

  4. Déterminer le minimum de $f$ sur $]0;+\infty[$.

  5. En déduire l’inégalité.

Code de déblocage de la correction :

Cette instruction supposons sera souvent utile pour étudier le signe d'un facteur contenant un paramètre.

Dans l'exemple précédent pour obtenir le maximum de $f$ sur $[0;2]$, il suffit de réduire l'étude directement à l'intervalle $[0;2]$ avec l'instruction supposons(t>=0 and t<=2) :

On peut remarquer le fait que la ligne 5 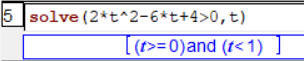donne une réponse directement sur $[0;2]$ contrairement à ce que l'on avait dans l'exemple où on travaillait sur $\mathbb{R}$.

On peut rajouter la ligne 8 suivante pour supprimer la condition portant sur t :
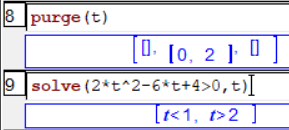
On remarque que la résolution de la ligne 9 est de nouveau sur $\mathbb{R}$ et non plus sur $[0;2]$.

On considère le circuit ci-contre dans lequel $E$, $r$ et $R$ ont des valeurs strictement positives. $R$ est la variable. La puissance dissipée dans le résistor de résistance $R$ est $P=\dfrac{RE^2}{(R+r)^2}$.

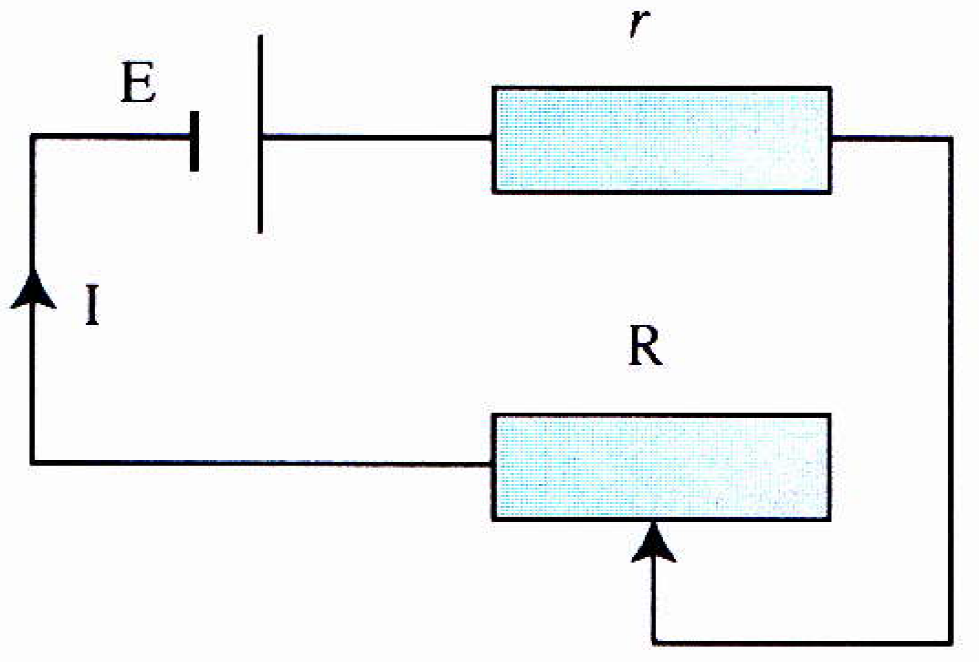
On considère la fonction $P:R\mapsto \dfrac{RE^2}{(R+r)^2}$ définie sur $]0;+\infty[$.

  1. Sur Xcas, exprimer la dérivée de $P$ sous forme factorisée en fonction de $E$ et de $r$.

  2. Rajouter sur Xcas une condition sur chaque paramètre $E$ et $r$ puis une condition sur la variable $R$.

  3. Sur Xcas, étudier le signe de chaque facteur de la dérivée.

  4. En déduire la construction du tableau de varaitions complet de la fonction $P$ sur $]0;+\infty[$.

  5. En déduire la valeur de $R$, en fonction de $E$ et de $r$, pour laquelle la puissance dissipée est maximale, ainsi que cette puissance maximale.

Code de déblocage de la correction :

Dans cet exercice, on étudie un filtre dont la transmittance isochrone de ce filtre a pour expression $T(j\omega)=R-j\times \dfrac{1}{C\omega + \frac{1}{\omega L}}$ où $j$ désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$ et où $R$, $L$, $C$ et $\omega$ désignent des nombres réels strictement positifs.

Soit $h$ la fonction définie par $h(\omega)= \dfrac{1}{C\omega + \frac{1}{\omega L}}$.

  1. Quels codes saisir successivement sur Xcas pour démonter que $h'(\omega)=\dfrac{(-L)\times(CL \omega^2-1)}{(CL\omega^2+1)^2}$ ?

  2. Quels codes doivent être saisis sur Xcas afin d'étudier le signe de chaque facteur de $h'$ ?

  3. Étudier précisément le signe de $h'$ sur $]0;+\infty[$ pour dresser le tableau de signes complet de $h$ sur $]0;+\infty[$.

  4. Déterminer en fonction de $C$ et de $L$ la valeur maximale de $h$.

  5. Est-il possible d'obtenir une valeur de $\omega$ permettant d'obtenir une valeur de $h(\omega)$ nulle ? Justifier.

Code de déblocage de la correction :

Exercices

Nombre dérivé

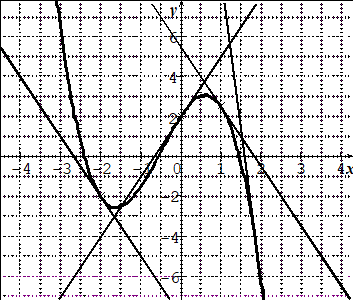
On considère la fonction $f$, définie sur $\mathbb{R}$, représentée par la courbe $\mathcal{C}$ ci-dessous et quelques tangentes.

  1. Lire graphiquement :

    1. $f(-2)$, $f(0)$, $f(1)$ et $f(2)$.

    2. $f'(-2)$, $f'(0)$, $f'(1)$ et $f'(2)$.

  2. Donner l'équation de chaque tangente.

  3. Y a-t-il des tangentes parallèles ? Justifier.

    1. Résoudre graphiquement $f(x)\ge 0$.

    2. Résoudre graphiquement $f'(x)\ge 0$.

  5. Dresser le tableau de variation de la fonction $f$.

Fonction dérivée

Déterminer à la main les dérivées des fonctions suivantes puis vérifier le résultat obtenu grâce à Xcas.

  1. $f(t)=4-3\times\dfrac{2}{9}t^4-\dfrac{\pi}{2} + \sqrt{2}t-\dfrac{7}{t^4}$+\dfrac{3}{t}.

  2. $f(t)=\dfrac{t^2-2t+4}{t+1}$.

  3. $f(t)=3(1-2t)^4$.

  4. $f(t)=3\cos(t)-\dfrac{5}{t^2}+4t\sin{t}$.

  5. $f(t)=t^2\ln(t)$.

  6. $f(t)=\sqrt{t^2+1}$.

  7. $f(t)=4\ln((t+1)^2)$.

  8. $f(t)=4+3t-\dfrac{6}{2-t}$.

  9. $f(t)=te^{\frac{1}{t}}$.

  10. $f(t)=\dfrac{(3-2t)^2}{e^t}$.

  11. $f(t)=A\sin(\omega t+\phi)$. ($A$, $\omega$ et $_phi$ sont des constantes réelles.)

Tangente

Un signal électrique $s_1$ est donné, pour $t\ge 0$, par $s_1(t)=(2t+3)e^{-t}$.

Afin de simplifier l'étude ultérieure de ce signal s1 on décide de l'approcher par un signal $s_2$ affine par morceaux. Ce signal $s_2$ est constitué d'une part par le segment formé par la tangente à la courbe $s_2$ entre le point d'abscisse 0 jusqu'à l'axe des abscisses puis d'autre part par l'axe des abscisses.

  1. Déterminer l'équation de la tangente à la courbe représentant la fonction $s_1$ au point d'abscisse 0.

  2. Déterminer l'expression du signal $s_2$ en fonction de $t$.

  3. Tracer les deux signaux pour vérifier la pertinence d'une telle approximation.

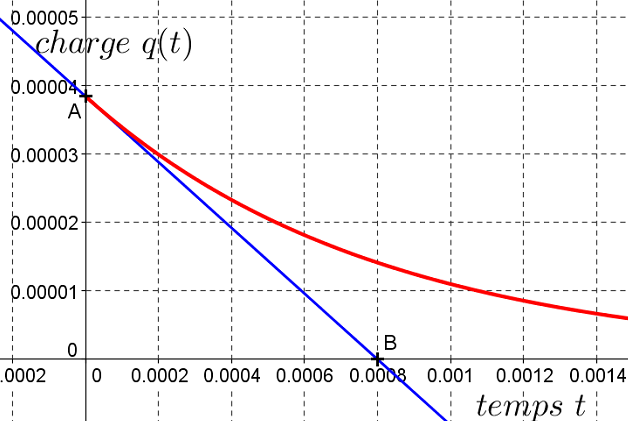
Un condensateur de capacité $C=1.6 \mu F$ branché aux bornes d'un conducteur ohmique de résistance $R$ se décharge. On modélise cette décharge en posant $q(t)=A\exp\left(-\dfrac{t}{\tau}\right)$ où $t$ représente le temps, exprimé en secondes et $\tau$ la constante de temps.

Le but est de déterminer la résistance $R$ du conducteur ohmique sachant que $\tau=RC$.

  1. Sachant que la charge initiale à $t=0$ du condensateur est $q_0=3.84\times 10^{-5}$, déterminer la valeur de $A$.

  2. Voici la décharge du condensateur :

    1. Déterminer le coefficient directeur de la tangente $T_0$ à la courbe représentative de la fonction $q$ au point d'abscisse 0.

    2. Déterminer la fonction dérivée de $q$.

    3. En déduire la valeur de $\tau$ puis la résistance du conducteur ohmique.

  3. Sachant, qu'à l'instant $t$, l'intensité, notée $i(t)$, est la dérivée de la charge, déterminer l'intensité à l'instant $t=0$.

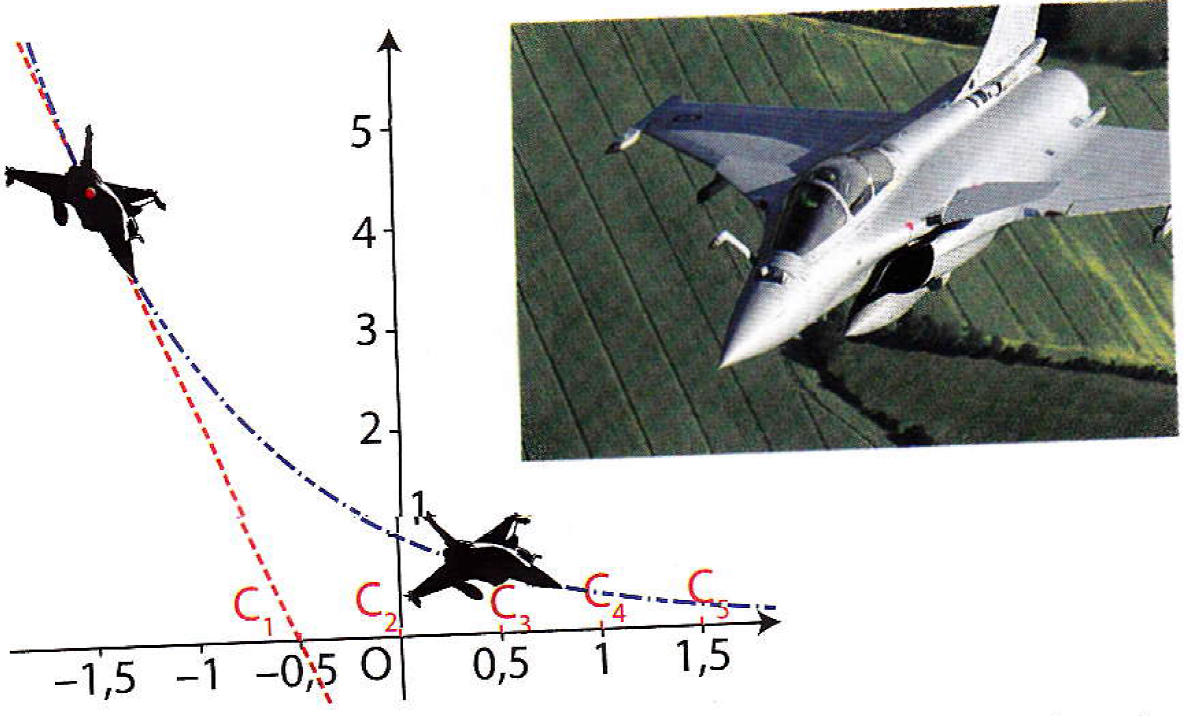
La figure ci-contre représente la trajectoire d'un avion de chasse qui descend de gauche à droite en suivant la courbe représentant la courbe d'équation $y=e^{-x}$.
En séance d'entraînement, le pilote doit simuler des tirs tangents à sa trajectoire pour atteindre 5 cibles $C_i$, pour $i$ allant de 1 à 5, placées au sol aux points d'abscisses respectives -0.5, 0, 0.5, 1 et 1.5.

  1. Quel cible sera atteinte si le pilote décide de tirer en position d'abscisse -1 ?

  2. Déterminer l'abscisse exacte de l'avion pour que le pilote atteigne la cible $C_5$.

  3. Déterminer l'abscisse exacte de l'avion pour que le pilote atteigne la cible $C_3$.

  4. Quelle doit être la position de l'avion s'il veut atteindre une cible se trouvant à l'abscisse $m$ ?

Utilisation de la dérivation

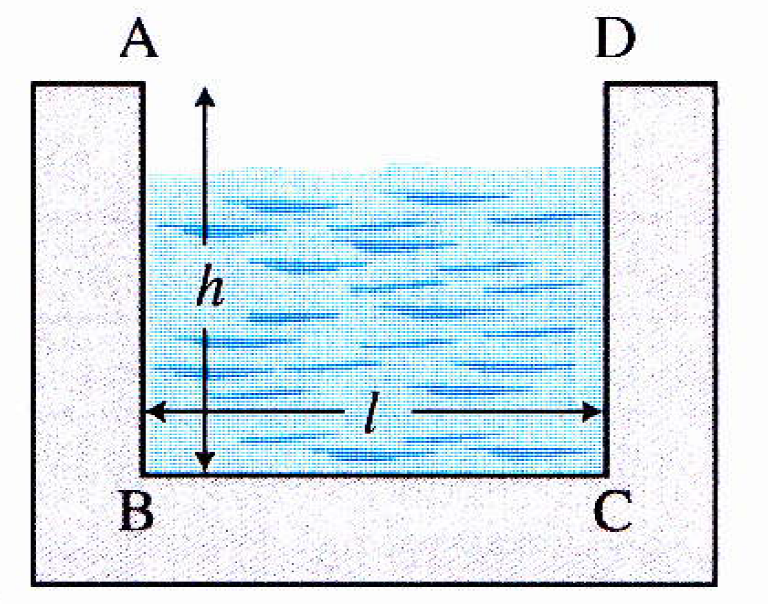
On veut, avant la construction, rendre minimal le frottement d'un fluide contre les parois d'un canal ouvert, de section intérieure rectangulaire ABCD. L'aire de la section intérieure de ce canal doit être de 0.5 $m^2$.
On désigne par $h$ la hauteur et par $l$ la largueur (en mètre) de cette section intérieure. On admettra que le frottement est minimal lorsque la longueur AB+BC+CD de la section intérieure est minimale.

  1. Justifier que $l=\dfrac{1}{2h}$.

  2. Justifier que la longueur AB+BC+CD est donnée par la fonction $g$ définie par $g(h)=2h+\dfrac{1}{2h}$.

  3. Déterminer la valeur de $h$ qui minimise le frottement et donner la valeur de $l$ qui lui correspond.

Code de déblocage de la correction :

La figure 1 ci-dessous représente un patron du parallélépipède de la figure 2 servant à contenir du lait. Ce patron est fabriqué à partir d’une feuille cartonnée carrée de 30 cm de côté.

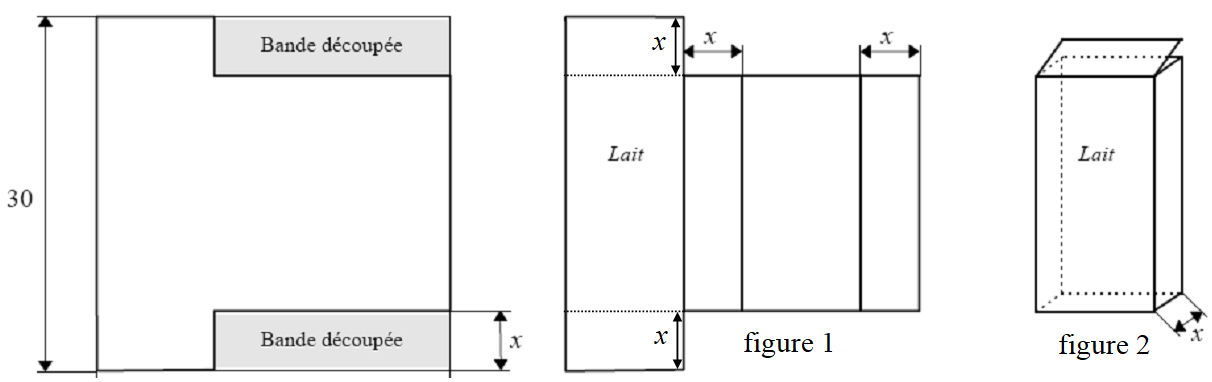
  1. Démontrer que le volume $V(x)$ du parallélépipède s'exprime en $cm^3$ par $V(x)=2x(15−x)^2$.

  2. Dresser le tableau de variation de $V$ sur $[0;15]$.

  3. Comment faut-il choisir $x$ pour que le volume $V(x)$ soit maximal ? Quel est ce volume maximal ?

Code de déblocage de la correction :

La vitesse avec laquelle un comprimé soluble, de volume donné, se dissout, augmente avec sa surface. Un laboratoire pharmaceutique fabrique un comprimé soluble de la forme d’un petit parallélépipède rectangle de volume 576 $mm^3$. On note $y$ sa hauteur, $x$ sa largeur et $2x$ sa longueur.

  1. Calculer $y$ en fonction de $x$.

  2. Montrer que la surface totale $S(x)$, en $mm^3$, de ce comprimé est $4x^2+ \dfrac{1728}{x}$.

  3. Montrer que $S'(x)= \dfrac{8(x-6)(x^2+6x+36)}{x^2}$.

  4. Étudier le sens de variation de $S$ sur $[3;12]$.

  5. En déduire la valeur de $x$ pour laquelle $S(x)$ est minimale.

Code de déblocage de la correction :

D'après un article publiée dans le n°455 de la revue scientifique La Recherche, l'évolution du niveau de la mer (en dm) sur la côté atlantique des États-Unis de 1000 à nos jours suit la courbe donnée par la fonction $f$ définie par $f(t)=(4t^2−2t+1)e^{2t}-1.08$.
Ici, $t=0$, pour l'an 1800 et $t=-1$ pour l'an 1400.

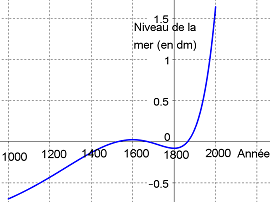
  1. Déterminer les points de la courbe en lesquels la tangente est horizontale.

  2. Selon cette étude, estimer au cours de quelle décennie le niveau de la mer :

    1. a été le plus élevé entre les années 1400 et 1800,

    2. a été le plus bas entre les années 1600 et 2000.

Un câble à section circulaire servant à transmettre un signal sous l'eau est constitué d'un noyau de fils de cuivre entouré d'un isolant non-conduteur.
$r$ est le rayon du noyau de cuivre et $h$ est l'épaisseur de l'isolant.
En notant $x= \frac{r}{h}$, on admet que la vitesse de transmission du signal est donné par $v(x)=x^2 \ln\left(\dfrac{1}{x}\right)$.

En considérant que le rayon du noyau est de 1 cm, quelle épaisseur donner à l'isolant afin d'assurer une vitesse de transmission maximale ?

Code de déblocage de la correction :

Une poutre de longueur $L$ placée sur deux appuis A et B subit une charge placée en son milieu $C$.

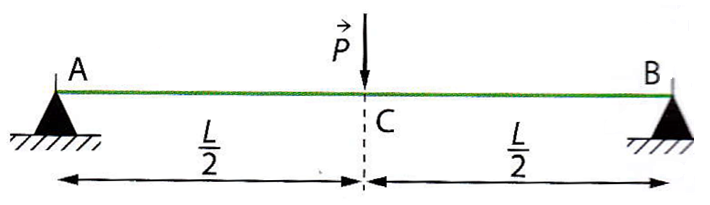
Elle se déforme. La courbe $\widehat{AB}$ représentant le profil de la poutre déformée est celui ci-dessous et on admet, que la résistance des matériaux conduit à ce que cette courbe entre les points $A$ et $C$ soit la représentation graphique de la fonction $g$ définie sur $\left[0;\dfrac{L}{2}\right]$ par $g(x)=\dfrac{P}{4EI}\left(\dfrac{1}{3} x^3-\dfrac{L^2}{4}x\right)$ où $P$, $E$ et $I$ sont des constantes physiques strictement positives.

  1. Étudier les variations de la fonction $g$ sur $\left[0;\dfrac{L}{2}\right]$.

  2. Démontrer que la distance $MC$, appelée "flèche maximale de la poutre" est donnée par $f=\dfrac{PL^3}{48EI}$.

Code de déblocage de la correction :

Le but du problème est l'étude de la désintégration d'un corps radioactif : le $\text{Thorium}^{227}$ qui donne est se désintégrant le $\text{Radium}^{223}$, lequel se désintègre à son tour en donnant du $\text{Radon}^{219}$.
On note $N_0$, le nombre d'atomes de $\text{Thorium}^{227}$ au temps $t=0$.

On admet que le nombre d'atomes de $\text{Radium}^{223}$ issu de cette désintégration est donnée en fonction du temps $t$ (en années) par $f(t)=\frac{19}{12} N_0\left( e^{-\frac{38}{1000}t}-e^{-\frac{62}{1000}t}\right)$.

  1. Déterminer $f(0)$. Interpréter ce nombre concrètement.

  2. Déterminer la limite de $f$ en $+\infty$. Interpréter ce nombre concrètement.

  3. Déterminer la valeur exacte $t_0$, puis une valeur approchée à $10^{-1}$ près de l'instant où $f'(t)=0$.

  4. Dresser le tableau de variations de $f$.
    Interpréter ce tableau d'un point de vue concret en utilisant un extremum.

Code de déblocage de la correction :

La fabrication de circuits électroniques nécessite de nombreuses étapes. Au cours de l’étape appelée dopage, des ions métalliques dits "dopants" sont introduits dans le silicium. Ces ions s'enfoncent progressivement dans le silicium. La quantité de dopants présents à la profondeur $d$ ($d>0$) s'exprime en fonction du temps $t$ ($t>0$) par $N(t)= \dfrac{1}{\sqrt{t}} e^{-\frac{2d^2}{t}}$.

  1. Démontrer que $N(t)$ est maximal pour une valeur $t_1$ du temps que vous déterminerez en fonction de $d$.

  2. En déduire $N(t_1)$.

Code de déblocage de la correction :

On se propose d'installer une rampe d'accès en pente douce permettant à des fauteuils roulant de franchir une marche à l'entrée d'une entreprise de service.
Les dimensions sont données en mètre sur la figure.

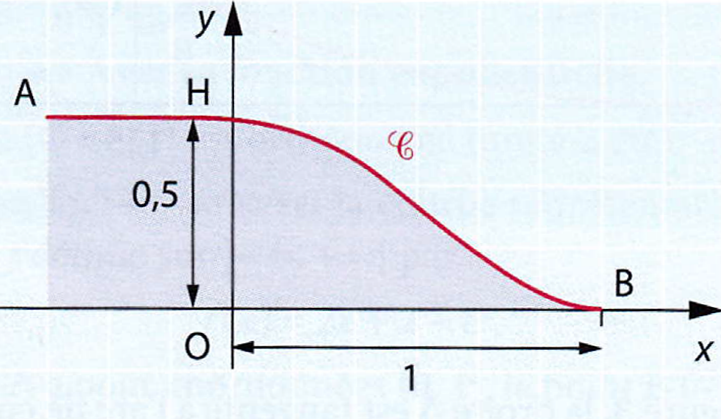
Le plan est muni du repère orthonormé $(O ; \overrightarrow{i}, \overrightarrow{j})$ d'axes $(Ox)$ et $(Oy)$.

La courbe $\mathcal{C}$ définie par le profil de la rampe doit être tangente en $B$ à l'axe des abscisses et en $H$ à la droite $(AH)$, $H$ étant sur l'axe des ordonnées.

Le but est de déterminer quatre réels $a$, $b$, $c$ et $d$ tels que la courbe $\mathcal{C}$ soit la courbe représentative de la fonction $f$ définie sur $[0;1]$ par $f(x)=ax^3+bx^2+cx+d$.

  1. Quelle doit être la pente de la tangente au point $B$ d'abscisse 1 ?
    En déduire que $3a+2b+c=0$.

  2. Justifier que $a$, $b$, $c$ et $d$ sont solutions du système : $\left\{ \begin{array}{r l l} 3a+2b+c &=0 \\ a+b+c+d &=0 \\ c &=0 \\ d &=1 \end{array} \right.$

  3. Déterminer quatre réels $a$, $b$, $c$ et $d$.

Lors d’un traitement par chimiothérapie en intraveineuse, la concentration du médicament dans l’organisme, exprimée en $\mu mol.L^{-1}$, peut être modélisée en fonction du temps $t$, exprimé en heure, par la fonction $c$ définie sur l’intervalle $[0;+\infty[$ par $c(t)=\dfrac{D}{k}\left(1-e^{-\frac{k}{80}t}\right)$, où :

La clairance traduit la capacité interne du patient à éliminer plus ou moins vite le médicament de son organisme. Elle est propre à chaque individu et est inconnue au début du traitement. Il est nécessaire de la déterminer afin que le médecin puisse adapter le traitement en ajustant le débit $D$.

  1. Détermination de la clairance

    Afin de déterminer la clairance, on effectue les mesures suivantes. On règle le débit de la perfusion sur 112 $\mu mol.h^{-1}$ ; au bout de 6 heures, on prélève un échantillon de sang du patient et on mesure la concentration du médicament : elle est égale à 6.8 $\mu mol.h^{-1}$.

    Déterminer une valeur approchée de la clairance de ce patient arrondie à $10^{-2}$ litre par heure près.

  2. Réglage du débit

    1. Déterminer la limite $L$ de la fonction $c$ en $+\infty$ en fonction du débit $D$ et de la clairance $k$.

    2. La concentration du médicament dans le sang se rapproche rapidement de sa limite $L$.

      Pour que le traitement soit efficace sans devenir toxique, cette concentration limite doit être de 16 $\mu mol.h^{-1}$.
      En déduire le débit $D$, à régler par le médecin, lorsque la clairance du patient est de 5.85 $L.h^{-1}$.

Code de déblocage de la correction :

L'épicéa commun est une espèce d’arbre résineux qui peut mesurer jusqu’à 40 mètres de hauteur et vivre plus de 150 ans. L’objectif de cet exercice est d’estimer l’âge et la hauteur d’un épicéa à partir du diamètre de son tronc mesuré à 1,30 m du sol.

Pour un épicéa dont l'âge est compris entre 20 et 120 ans, on modélise la relation entre son âge (en années) et le diamètre de son tronc (en mètre) mesuré à 1,30 m du sol par la fonction $f$ définie sur l'intervalle $]0;1[$ par : $f(x) = 30\ln\left(\dfrac{20x}{1−x}\right)$, où $x$ désigne le diamètre exprimé en mètre et $f(x)$ l’âge en années.

  1. Déterminer comment varie l’âge en fonction du diamètre.

  2. Déterminer les valeurs extrêmes du diamètre $x$ du tronc tel que l'âge calculé dans ce modèle reste conforme à ses conditions de validité, c’est-à-dire compris entre 20 et 120 ans.

  3. Déterminer l’âge d’un épicéa dont le diamètre du tronc mesuré à 1,30 m du sol vaut 27 cm.

  4. Déterminer le diamètre du tronc mesuré à 1,30 m du sol d’un épicéa âgé de 100 ans.

  5. La qualité du bois est meilleure au moment où la vitesse de croissance est maximale. On admet que ce maximum est atteint lorsque $f'$ est minimal.

    1. Déterminer l'âge où la qualité du bois est la meilleure en expliquant la démarche.

    2. Est-il cohérent de demander aux bûcherons de couper les arbres lorsque leur diamètre mesure environ 70 cm ?

Une feuille rectangulaire $ABCD$ au format A4, 21 cm par 29.7 cm, est pliée selon un segment $[MN]$ de telle manière à ce que le point $B$ se retrouve en un point $L$ du segment $[AD]$.

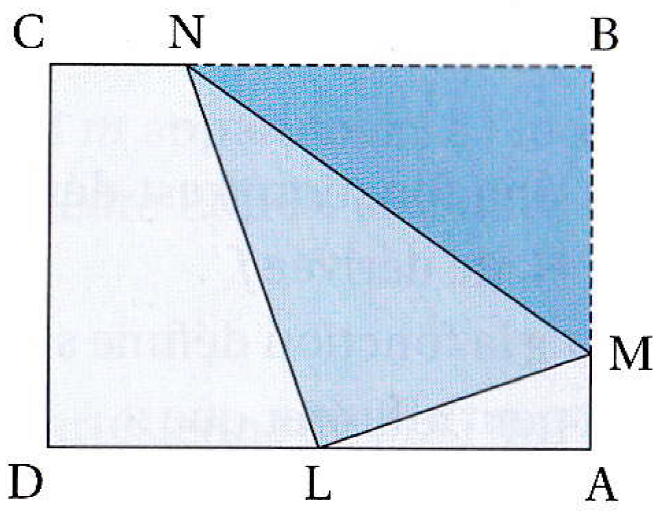
Le but de l'exercice est de savoir s'il est possible de minimiser la longueur du segment $[MN]$.
On note $x$ la longueur de $[BM]$ et $y$ celle de $[MN]$.
On admet que $y=\sqrt{\dfrac{2x^3}{2x−21}}$.

  1. Étudier les variations de $f:x\mapsto \sqrt{\dfrac{2x^3}{2x−21}}$ sur $]10.5;21]$.

  2. Prouver que $f$ admet un minimum en $x=\alpha$ à déterminer.

  3. Déterminer alors la longueur BN.
    Est-il possible de partager au format A4 de manière à minimiser la longueur du segment [MN] ?

Demander le programme !

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲