Fonctions cube, inverse et racine carrée

Voici trois courbes, chacune correspondant à une des trois fonctions de la définition.
Compléter chacune des phrases avec les mots cube, inverse et racine carrée puis cliquer sur le bouton Vérifier pour tester les réponses saisies.

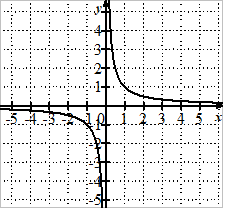  1. Cette courbe représente la fonction .

  2. Cette courbe représente la fonction .

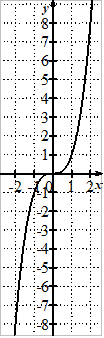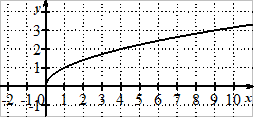  3. Cette courbe représente la fonction .

Il est essentiel d'avoir à l'esprit l'allure générale de la courbe représentant chacune de ces trois fonctions.

Pour obtenir $\sqrt{t}$ sur Xcas, il suffit de saisir sqrt(t).

Accorder une guitare, c'est régler la tension des cordes afin qu'elles donnent les sons fondamentaux.
Les physiciens ont démontrés que la fréquence du son d'une corde est proportionnelle à la racine carrée de la tension de cette corde. Supposons que, pour une corde donnée la fréquence $N$ de la note (en Hertz) soit donnée par $N(T)=10\sqrt{T}$, où $T$ est la tension de la corde exprimée en Newton.

  1. Quelle est la fréquence du son émis lorsque la tension est de 625 Newtons ?

    2. Code de déblocage de la correction :

  2. Quelle est la tension de la corde si elle émet un $sol_2$ de 196 Hertz ?

    3. Code de déblocage de la correction :

  3. Les sons émis par cette corde deviennent identifiables lorsque la tension est supérieure à 250 Newtons et elle casse si la tension dépasse 750 Newtons. Est-il possible avec cette corde d'obtenir :

    1. Un $do_2$ de 131 Hertz ?

    2. Un $si_2$ de 247 Hertz ?

    3. un $ré_3$ de 294 Hertz ?

    4. Code de déblocage de la correction :

Et l'unique cordeau des trompettes marines
Guillaume Apollinaire

Notion de limite

On peut connaître le comprtement de la fonction là où elle est définie.
Mais que se passe-t-il aux bornes de son ensemble de définition ?
Le but de cette partie est de comprendre le comportement d'une fonction en l'infini ou bien en des endroits particuliers comme des valeurs interdites.

Si on calcule les images de la fonction cube pour des valeurs de $t$ très grandes, on obtient le tableau de valeurs suivant :

$t$ $10$ $10^6$ $10^{10}$ $10^{100}$ ...
$t^3$ $10^3$ $10^{18}$ $10^{30}$ $10^{300}$ ...

On devine que ces images $t^3$ peuvent être aussi grandes que l'on veut dès que $t$ est suffisamment grand.

On parle dans ce cas de limite infinie.

Soit $f$ une fonction définie sur un intervalle $]a;+\infty[$.

Si les images de $f$ peuvent être aussi grande que l'on veut dès que $t$ est suffisamment grand, on dit que $f$ tend vers $+\infty$ lorsque $t$ tend vers $+\infty$, ce qui se note :
$\displaystyle{\lim_{t\rightarrow +\infty}{f(t)}=+\infty}$

Si on calcule les images de la fonction cube pour des valeurs de $t$ très grandes, on obtient le tableau de valeurs suivant :

$t$ $10$ $10^6$ $10^{10}$ $10^{100}$ ...
$\dfrac{1}{t}$ $0.1$ $10^{-6}$ $10^{-10}$ $10^{-100}$ ...

On devine que ces images $\dfrac{1}{t}$ peuvent être aussi proche de 0 que l'on veut dès que $t$ est suffisamment grand.

On parle dans ce cas de limite finie valant 0.

Soit $f$ une fonction définie sur un intervalle $]a;+\infty[$.

Si les images de $f$ peuvent être aussi proche d'un réel $L$ que l'on veut dès que $t$ est suffisamment grand, on dit que $f$ tend vers $L$ lorsque $t$ tend vers $+\infty$, ce qui se note :
$\displaystyle{\lim_{t\rightarrow +\infty}{f(t)}=L}$

Recopier et compléter les limites des fonctions usuelles en s'aidant de leur courbe représentative.

  1. $\displaystyle{\lim_{t\rightarrow +\infty}{t^3}= ...}$

  2. $\displaystyle{\lim_{t\rightarrow -\infty}{t^3}= ...}$

  3. $\displaystyle{\lim_{t\rightarrow +\infty}{\sqrt{t}}= ...}$

  4. $\displaystyle{\lim_{t\rightarrow 0}{\sqrt{t}}= ...}$

On peut retrouver ces limites à l'aide de Xcas avec l'instruction limit(fonction,variable,borne)

Par exemple, on peut obtenir la limite $\displaystyle{\lim_{t\rightarrow +\infty}{\sqrt{t}}}$ avec la saisie limit(sqrt(t),t,+inf)

Vérifier toutes les limites obtenues à l'exercice précédent grâce à Xcas.

Lorsque les valeurs de $t$ tendent vers un réel $a$ en restant toujours supérieur à ce réel, on parle de limite à droite. On note alors : $\lim\limits_{\substack{t \rightarrow a \\ t>a}} f(t)$

Recopier et compléter les limites de la fonction inverse en s'aidant de sa courbe représentative.

  1. $\displaystyle{\lim_{t\rightarrow +\infty}{\dfrac{1}{t}}= ...}$

  2. $\displaystyle{\lim_{t\rightarrow -\infty}{\dfrac{1}{t}}= ...}$

  3. $\lim\limits_{\substack{t \rightarrow 0 \\ t>0}} \dfrac{1}{t}= ...$

  4. $\lim\limits_{\substack{t \rightarrow 0 \\ t\lt0}} \dfrac{1}{t}= ...$

On peut retrouver ces limites à droite ou à gauche sur Xcas en rajoutant un quatrième argument -1 (pour limite à gauche) ou +1 (pour avoir la limite à droite) à l'instruction l'instruction limit.

Par exemple, on peut obtenir la limite à gauche $\lim\limits_{\substack{t \rightarrow 0 \\ t\lt0}} \dfrac{1}{t}$ avec la saisie limit(1/t,t,0,-1)

S'aider de l'aide proposer par Xcas pour gérer les arguments de cette instruction limit.

Vérifier toutes les limites obtenues à l'exercice précédent grâce à Xcas.

Fonction exponentielle

La fonction exponentielle est la seule fonction $f$ dérivable sur $\mathbb{R}$ vérifiant pour tout réel $t$ : $f′(t)=f(t)$ avec $f(0)=1$.
On la note $f:t\mapsto e^t$ ou $exp$.

Voic la courbe représentative de la fonction exponentielle :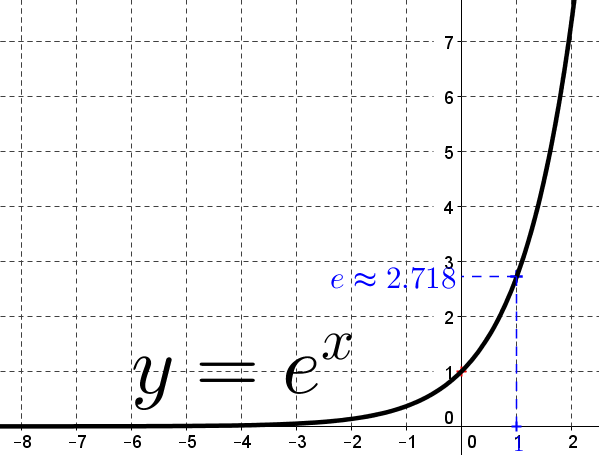

On note $e$ l'image de 1 par la fonction exponentielle, c'est-à-dire $e=e^1$.

Pour obtenir $e^t$ sur Xcas (ou sur Geogebra), il suffit de saisir : e^t ou exp(t).

  1. Déterminer, à l'aide de la représentation graphique, les limites de la fonction exponentielle en $-\infty$ et en $+\infty$.

  2. Vérifier ces deux limites en utilisant Xcas.

Ces deux limites sont à connaître : connaître l'allure de la courbe représentant la fonction exponentielle permet de retrouver ces résultats.

Pour tout réel $x$ et $y$, on a :

  1. $e^x >0$

  2. $e^x=e^y \iff x=y$

  3. $e^x > e^y \iff x>y$

Résoudre l'équation suivante d'abord à la main, puis sur Xcas : $e^{2\times t}=e^{2+t}$

La fonction exponentielle a les même propriétés algébriques que celles algébriques sur les puissances :
la fonction exponentielle transforme les sommes en multiplication et les multiplications en exponentiation.

Plus précisément :

Pour tout réel $a$ et $b$ et pour tout entier $n$, on a :

  1. Résoudre à la main l'inéquation $e^{3t-1}\lt e^t\times e^{t+3}$.

  2. Vérifier sur Xcas.

Voici des propriétés découlant des propriétés algébriques précédentes :

Pour tout réel $a$ et $b$ et pour tout entier $n$, on a :

  1. $e^{a-b}=\dfrac{e^a}{e^b}$

  2. $\sqrt{e^a}=e^{\frac{a}{2}}$

On étudie l'évolution d'une population de larves vivantes d'insectes en fonction du temps.
Une partie des larves vivantes devient des insectes qui pondront des œufs qui donneront à leur tour des larves vivantes.

On admet que sous certaines conditions, le nombre de ces larves vivantes dans un laboratoire est donnée par la fonction $f$ définie par $f(t)=6000e^{-0.2t}−5000e^{-0.3t}$ où $t$ est en jours.

  1. Déterminer la population initiale.

  2. Quand la population de larves vivantes vaut-elle 500 individus ?

  3. Quand la population de larves vivantes vaut-elle 1200 individus ?

  4. Que penser de la population de larves à très long terme dans ce laboratoire ?

On s’intéresse à l’évolution de la hauteur d’un plant de maïs en fonction du temps.

Le graphique suivant représente cette évolution. La hauteur est en mètres et le temps en jours.

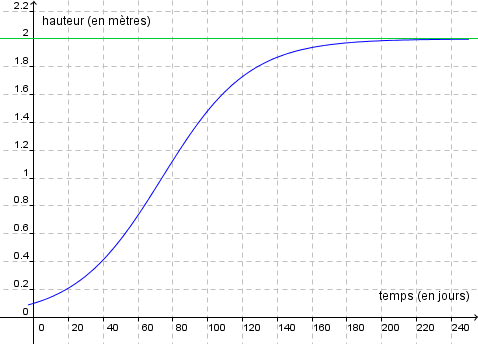
On décide de modéliser cette croissance par une fonction logistique du type : $h(t)=\dfrac{a}{1+be^{-0.04t}}$, où $a$ et $b$ sont des constantes réelles positives, $t$ est la variable temps exprimée en jours et $h(t)$ désigne la hauteur du plant, exprimée en mètres.

On sait qu’initialement, pour $t=0$, le plant mesure 0,1 m et que sa hauteur tend vers une hauteur limite de 2 m.

  1. Traduire en une équation mathématique la phrase "initialement, pour $t=0$, le plant mesure 0,1 m ".

  2. Déterminer, en utilisant Xcas, les constantes $a$ et $b$ afin que la fonction h corresponde à la croissance du plant de maïs étudié.

  3. Vérifier les constantes obtenues en traçant la fonction $h$ obtenue sur Geogebra.

Fonction logarithme népérien

L’équation $e^y=t$, où $t$ est un réel strictement positif, admet une unique solution dans $\mathbb{R}$. La solution $y$ de $e^y=t$ est appelée logarithme népérien de $t$ et est notée $\ln(t)$.

La fonction logarithme népérien notée $\ln$, est la fonction définie sur $]0;+\infty[$ qui a tout réel strictement positif $t$, associe le réel noté $\ln(t)$ dont l’exponentielle est $t$.

Le nombre $a$ tel que $e^a=3$ est le réel $a=\ln(3)$.

  1. $\ln(1)=0$ (car $1=e^0$)

  2. $\ln(e)=1$ (car $e=e^1$)

  3. Pour tout réel $t$ strictement positif et tout réel $y$, $e^y=t$ équivaut à $y=\ln(t)$

  4. Pour tout réel $t$ strictement positif, $e^{\ln(t)}=t$.

  5. Pour tout réel $t$, $\ln(e^{t})=t$.

Les deux derniers points signifient que les fonctions $exp$ et $\ln$ sont réciproques l’une de l’autre.

  1. $e^{\ln(8)}=8$

  2. $\ln{e^{3x+2}}=3x+2$

  3. $\ln(t)=4 \iff t=e^4$

Dans un repère orthonormal, les courbes représentatives des fonctions exponentielle et logarithme népérien sont symétriques par rapport à la droite d’équation $y=x$. D'où, la courbe représentative à connaître par coeur :

Sur Xcas (et sur Geogebra), pour obtenir $\ln(t)$, il suffit de saisir ln(t)

  1. À l'aide de la représentation graphique de la fonction $\ln$, déterminer les limites aux deux bornes de son ensemble de définition.

  2. Vérifier sur Xcas ces deux limites.

Code de déblocage de la correction :

Pour tout réel $a$ et $b$ strictement positifs, on a :

En utilisant les propriétés précédentes, résoudre à la main les équations suivantes puis vérifier les solution obtenues sur Xcas.

  1. $\ln(t)=0$

  2. $4e^t-1=2$

  3. $\ln(3t)=\ln(3+t)$

  4. $\ln(t)+\dfrac{1}{2}=0$

  5. $e^{2t}+3=5$

  6. $1+\ln(3-t)=0$

  7. $\ln(e^t)=2e^{\ln(t)}+1$

Code de déblocage de la correction :

À l'inverse de la fonction exponentielle, la fonction logarithme népérien transforme les produits en somme et les puissances en produit. Plus précisément :

Pour tout réel $a$ et $b$ strictement positifs et pour tout entier $n$, on a :

Résoudre à la main l'équation suivante puis vérifier le résultat obtenu sur Xcas :
$3\ln(e\times t)+2=1−4\ln(t)$

Le carbone 14 est un isotope radioactif du carbone permettant de dater les restes d'êtres vivants.
La formule suivante donne l'âge $T$, en nombre d'années, d'un échantillon en fonction du pourcentage $p$ de carbone 14 restant au bout de $T$ années : $T=8264\ln\left(\dfrac{100}{p}\right)$.

  1. Le squelette d'un homme de Neandertal contient 2% du carbone 14 initialement contenu dans ses os. Estimer à quand remonte ce squelette.

  2. La datation au carbone 14 a permis d'estimer l'âge d'une momie à 2500 ans. Quelle proportion de carbone 14 a été mesurée dans la momie.

Exercices

Un sonomètre est placé à une distance $R$ en mètres d'une machine-outil.
Le niveau d'intensité sonore en décibels (dB) qu'il mesure est donnée par la fonction : $L:R\mapsto 129−20 \dfrac{\ln(R)}{\ln10}$.

  1. Calculer l'intensité sonore à 1 mètre de la machine-outil.

  2. L'intensité maximum supportable par une oreille normale est de 120 décibels. À quelle distance minimale de la machine-outil un travailleur sans casque de protection doit-il se trouver ?

La glycémie est le taux de glucose dans le sang. On observe la glycémie d'un individu après l'ingestion d'une boisson sucrée. On considère que la glycémie (en grammes par litre) en fonction du temps $t$ écoulé (en heures) est donnée par la formule : $g(t)=\ln(3t+1)−t+0.8$.

  1. Quelle est la glycémie au moment de l'ingestion de la boisson sucrée.

  2. Calculer le taux de glucose dans le sang 15 minutes après ingestion.

  3. Tracer sur Geogebra la fonction g.

  4. Déterminer l'ensemble des instants où la glycémie dépasse 1 g/L.

La magnitude apparente $M$ d'un astre est la mesure du rayonnement d'un objet céleste observé depuis la Terre.
On admet que la magnitude apparente $M$ d'un astre d'éclat $E$ est définie par $M=-2.5\dfrac{\ln\left(\dfrac{E}{E_0}\right)}{\ln(10)}$, où $E_0$ est l'éclat apparent de l'étoile Véga, prise comme référence.

  1. Quelle est la magnitude apparente de Véga ?

  2. L'étoile le plus brillante du ciel nocturne est Sirius. Son éclat est 3.9 fois celui de Véga. Quelle sa magnitude apparente ?

  3. La magnitude du soleil est -26.7. Calculer le rapport entre l'éclat du soleil et celui de Sirius.

La fonction de croissance de von Bertalanfty donne approximativement la taille moyenne $L(t)$ (en centimètres) à l'âge $t$ (en années) des poissons Arius latiscutatus, mâchoiron de Gambie, péchés dans le Golfe de Guinée.

On admet que $L(t)=68.3\times\left(1−e^{−K(t+0.819)}\right)$, où $K$ est une constante correspondant à un coefficient de croissance qui dépend de l'espèce.

  1. Sachant qu'en moyenne un tel poisson mesure 54 cm à l'âge de 7 ans, déterminer la valeur de $K$, arrondie à 0.0001 près.

  2. Quelle est la taille moyenne d'un mâchoiron de Gambie âgé de un an ?

  3. Quelle est la taille moyenne d'un très vieux mâchoiron de Gambie ? Explicitez votre démarche.

  4. On admet que le poids moyen en grammes $W(t)$ d'un mâchoiron de Gambie âgé de t années de taille $L(t)$ est donné approximativement par : $W(t)=0.01176\times (L(t))^3$.

    1. Déterminer le poids moyen d'un mâchoiron âgé de 2 ans.

    2. Déterminer l'âge moyen, arrondi au mois près, d'un mâchoiron pesant 1 kilogramme.

    5. source des données utilisées

Une étude a montré que la charge électrique d'un composant électronique en fonction du temps en secondes est donné par $c(t)=25(1−e^{-2t})$.

    1. Tracer sur Geogebra la courbe $\mathcal{C}$ représentant la fonction $c$.

    2. Déterminer une valeur arrondie au dixième de l'instant $t_0$ où la charge dépasse 20.

    1. Résoudre de manière exacte l'inéquation $c(t)>20$. En déduire la valeur exacte de $t_0$.

    2. Vérifier sur un logiciel cette valeur exacte puis celle approchée lue.

Le plastique acrylique est une matière transparente plus résistance que le verre.
Pour calculer le pourcentage de lumière traversant une plaque de plastique acrylique, on utilise la fonction $P$ définie sur $]0;+\infty[$ par $P(x)=100e^{-0.015x}$, où $x$ est l'épaisseur, en cm, de cette plaque.

  1. Quelle pourcentage de lumière traverse une plaque de 30 cm ?

  2. Quelle doit être l'épaisseur de la plaque si l'on veut que 75% de la lumière soit bloquée ?

  3. Quel semble être le sens de variations de $P$ ?

  4. Quelle est la limite en $+\infty$ de $P$ ? Quelle interprétation concrète en donner ?

Aujourd'hui plus de 80 % du trafic mondial longue distance se fait par des fibres optiques. Ces dernières ont en effet de multiples avantages par rapport aux câbles électriques classiques.
Elles offrent la possibilité de transmettre des données, de la voix, des images… à de très hauts débits.

Une fibre optique est jugée performante lorsque, sur une longueur donnée, la puissance du signal qu'elle transmet subit une perte minimale.

Pour un signal d’entrée de puissance fixée, la puissance lumineuse à la sortie d’une fibre optique dépend de sa longueur $L$. Cette puissance de sortie $P_S$ est modélisée par la formule suivante : $P_S=5e^{-0.2L}$, où $P_S$ est la puissance en milliwatts (mW) et $L$ la longueur en kilomètres (km).

Lorsque le signal perd 90 % de sa puissance, il nécessite une amplification.
Au bout de combien de kilomètres le signal transmis par la fibre doit-il être amplifié ?

Partie A : déterminer un vol parabolique

En décrivant des paraboles, l'airbus "A300 zéro G" permet de simuler l'impesanteur.
La trajectoire étudiée est modélisée ainsi : Dans le repère $(O ; Ox ; Oy)$ dont l'unité choisie sur les deux axes est le mètre, l'ordonnée de l'avion en fonction de la valeur de $x$ est indiquée par la relation de la forme suivante : $y=ax^2+bx$.

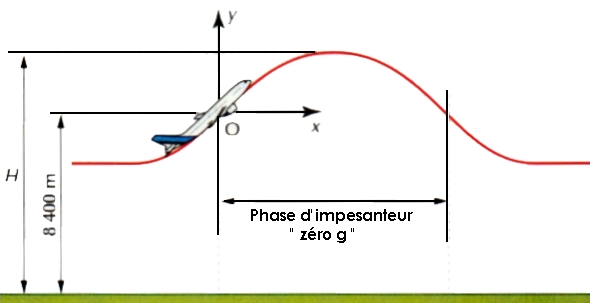
Lors de la trajectoire, deux positions sont relevées : l'avion passe par les points $A(1000;750)$ et $B(3000;750)$.

  1. Utiliser les points $A$ et $B$ afin d'écrire un système vérifié par les réels $a$ et $b$.

  2. Résoudre le système sur obtenu afin de trouver $a$ et $b$.

  3. Atteint-on l'altitude de 10000 m lors d'un tel vol parabolique ?
    Si oui, pour quelle(s) valeur(s) de $x$ ; si non, quelle est l'altitude maximale atteinte ?

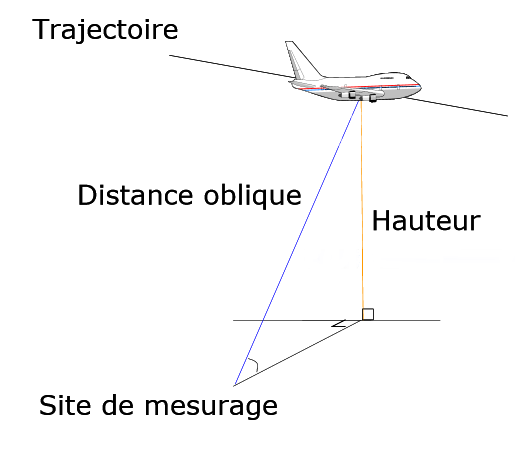
Partie B : déterminer la distance séparant un observateur d'un airbus A380

Le niveau sonore perçu par une personne décroit avec la distance séparant cette personne de l'avion.
Le niveau sonore $N$ (exprimé en dB) perçu à l'arrivée de l'airbus A380 est fonction de la distance oblique $d$, exprimée en mètre. Le niveau sonore est alors donné par la relation : $N=-14.67\ln(d)+170$.

  1. Déterminer la distance séparant l'avion du site de mesurage lorsque le niveau d’intensité sonore mesuré est de 60 dB.

La température $\theta$ d’une huile de moteur varie en fonction du temps $t$ de fonctionnement suivant l’expression : $\theta=250−100e^{-kt}$ avec $\theta$ la température de l'huile en °C, $k$ une constante et $t$ le temps de fonctionnement en minutes.

  1. La température de l’huile est de 190°C après 5 minutes de fonctionnement.
    Déterminer la valeur de la constante $k$.

  2. Si l'huile ne doit pas dépasser la température de 220°C, combien de temps peut fonctionner le moteur ?

  3. Si l'huile ne doit pas dépasser la température de 280°C, combien de temps peut fonctionner le moteur ?

La société AXON’CABLE est une entreprise régionale installée à MONTMIRAIL dans le sud de la Marne. Parmi ses produits figurent des câbles coaxiaux.
Voici des extraits de leur documentation :

L’étude qui suit vise à observer l’évolution de l’impédance caractéristique du câble en fonction de son diamètre de diélectrique.
Dans toute la suite du problème, on considèrera que le diélectrique est du PTFE (polytétrafluoréthylène) de constante diélectrique $ε=2.1$ et on ne s'intéressera qu'aux câbles dont le conducteur central est $d=0.3$ mm.

  1. Sachant que $log_{10}(x)=\dfrac{\ln(x)}{\ln(10)}$, afficher sur Geogebra la courbe représentant l'impédance caractéristique du câble en fonction du diamètre $D$ du diélectrique.
    L'impédance semble diminuer ou augmenter lorsque le diamètre $D$ du diélectrique augmente ?

  2. Dans un second document de l'entreprise, on trouve les informations suivantes :

    1. Lorsque le diélectrique a pour diamètre $D=0.85$ mm alors l'impédance est $Z_C=50$ $\Omega$.

    2. Lorsque le diélectrique a pour diamètre $D=1.65$ mm alors l'impédance est $Z_C=75$ $\Omega$.

    Ces informations sont-elles correctes ?

  3. Si on veut une impédance $Z_C$ de 95 $\Omega$, quel doit être le diamètre du diélectrique du câble ?

Demander le programme !

Licence Creative Commons
Les différents auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

▲