Nous allons étudier dans ce chapitre la notion d'intégration.
Cette notion est une notion fondamentale en analyse. Elle est très utile pour évaluer des aires,
pour calculer la valeur moyenne d'une fonction, la valeur efficace d'une fonction de transfert, ...
La notion d'intégration a été développée à partir du XVIIè siècle suite aux travaux indépendants d' Isaac Newton et de Gottfried Leibniz, même si des prémices du calcul infinitésimal sont étudiés dès l'antiquité avec Archimède.
Dans tout ce chapitre, $f$ est une fonction définie sur un intervalle $I$ dont la courbe représentative est notée $\mathcal{C}_f$ dans un repère orthogonal. $a$ désigne un réel quelconque de l'intervalle $I$.
Primitive
Définition
Soit $f$ une fonction définie sur un intervalle $I$.
Une fonction $F$ est une primitive de $f$ sur $I$ si $F$ est dérivable sur $I$ et si $F'=f$.
-
Une primitive de $t\mapsto 2t$ est $t\mapsto t^2$ car $(t^2)'=2t$.
-
Une primitive de $t\mapsto t^3+\cos(t)$ est $t\mapsto \dfrac{1}{4}t^4+\sin(t)$ car $(t^4)'=4t^3$ et $(\sin(t))'=\cos(t)$.
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(t)=3e^t+4+\dfrac{1}{t^2}$.
-
Prouver que la fonction $F$ définie sur $]0;+\infty[$ par $F(t)=3e^t+4t-\dfrac{1}{t}+2$ est une primitive de $f$ sur $]0;+\infty[$.
-
Comme modifier l'expression de $F$ pour obtenir une autre primitive de $f$ sur $]0;+\infty[$ ?
-
-
Calculer la valeur de $F(1)$.
-
Déterminer une primtive $G$ de $f$ sur $]0;+\infty[$ telle que $G(1)=3e$.
-
Soit $f$ une fonction définie sur $I$.
-
Si $F$ est une primitive de $f$ sur $I$ alors $f$ admet une infinité de primitives : ce sont toutes les fonctions $G$ définies par $G(t)=F(t)+C$, où $C$ est une constante réelle.
-
Pour tout réel $a$ et $b$ tels que $a\in I$, il existe une unique primtive $G$ de $f$ sur $I$ telle que $G(a)=b$.
Primitives des fonctions usuelles
Le tableau ci-dessous donne la forme générale des primitives des fonctions usuelles en mathématiques.
Dans ce tableau, $C$ désigne une constante réelle.
Les 3 formules essentielles à connaître sont celles mises en gras, elles sont à connapitre par coeur ! :
| Fonction $f$ définie sur $I$ par | Les primitives de $f$ sur $I$ sont définies par | Intervalle $I$ |
|---|---|---|
| $f(t)=k$ $(k\in\mathbb{R})$ | $F(t)=kt+C$ | $\mathbb{R}$ |
| $f(t)=at+b$ $(a\in\mathbb{R}, (b\in\mathbb{R})$ | $F(t)=\dfrac{1}{2}at^2+bt+C$ | $\mathbb{R}$ |
| $f(t)=t^n$ ($n\in\mathbb{N}$ avec $n\neq 0$) | $F(t)=\dfrac{t^{n+1}}{n+1}+C$ | $\mathbb{R}$ |
| $f(t)=t^{\alpha}$ ($\alpha\in\mathbb{R}$ avec $\alpha\neq 0$) | $F(t)=\dfrac{t^{\alpha+1}}{\alpha+1}+C$ | $]0;+\infty[$ |
| $f(t)=\dfrac{1}{t^2}$ ($=t^{-2}$) | $F(t)=-\dfrac{1}{t}+C$ ($=\dfrac{t^{-2+1}}{-2+1}+C$) | $]0;+\infty[$ ou $]-\infty;0[$ |
| $f(t)=\dfrac{1}{t^n}$ ($=t^{-n}$ avec $n\in\mathbb{N}$ et $n\le 2$) | $F(t)=-\dfrac{1}{n-1}\dfrac{1}{t^{n-1}}+C$ ($=\dfrac{t^{-n+1}}{-n+1}+C$) | $]0;+\infty[$ ou $]-\infty;0[$ |
| $f(t)=\dfrac{1}{t}$ | $F(t)=\ln(t)+C$ | $]0;+\infty[$ |
| $f(t)=\dfrac{1}{\sqrt{t}}$ ($=t^{-\frac{1}{2}}$) | $F(t)=2\sqrt{t}+C$ ($=\dfrac{t^{-n+1}}{-n+1}+C$) | $]0;+\infty[$ |
| $f(t)=e^t$ | $F(t)=e^t+C$ | $\mathbb{R}$ |
| $f(t)=\sin(t)$ | $F(t)=-\cos(t)+C$ | $\mathbb{R}$ |
| $f(t)=\cos(t)$ | $F(t)=\sin(t)+C$ | $\mathbb{R}$ |
| $f(t)=\dfrac{1}{1+t^2}$ | $F(t)=Arctan(t)+C$ | $\mathbb{R}$ |
Utiliser le tableau ci-dessus pour déterminer une primitive $F$ de chacun des fonctions $f$ suivantes sur l'intervalle $I$ proposé :
-
$f(t)=t^4$ sur $I=\mathbb{R}$.
-
$f(t)=\dfrac{1}{t^6}$ sur $I=]0;+\infty[$.
-
$f(t)=e^t+\dfrac{2}{t}$ sur $I=]0;+\infty[$.
-
$f(t)=t^2-1$ sur $I=\mathbb{R}$.
Opérations sur les primitives
Comme lors de la dérivation, our calculer à la main les primitives de fonctions plus compliquées, il faudra commencer par repérer la forme globale de la fonction puis d'utiliser le tableau suivant.
Dans ce tableau, $C$ désigne une constante réelle.
Les 3 formules essentielles à connaître sont celles mises en gras, elles sont à connapitre par coeur ! :
| Forme de la fonction $f$ définie sur $I$ par | Les primitives de $f$ sur $I$ sont définies par | Conditions éventuelles sur $u$ et sur l'ntervalle $I$ |
|---|---|---|
| $f=u'+v'$ (somme de fonctions) | $F=u+v+C$ | aucune |
| $f=k\times u'$ (produit par une constante) | $F=k\times u+C$ | aucune |
| $f(t)=\cos(\omega t+\phi)$ | $F(t)=\dfrac{1}{\omega}\sin(\omega t +\phi)+C$ | aucune |
| $f(t)=\sin(\omega t+\phi)$ | $F(t)=-\dfrac{1}{\omega}\cos(\omega t +\phi)+C$ | aucune |
| $f=ku' u^n$ ($n\in\mathbb{N}$ et $n\neq 1$) | $F=k\dfrac{u^{n+1}}{n+1}+C$ | $u>0$ sur $I$ |
| $f=ku' e^u$ | $F=k e^u+C$ | aucune |
| $f=k\dfrac{u'}{u}$ | $F=k\ln(u)+C$ | $u>0$ sur $I$ |
La première formule en gras est utile dans de nombreux cas. Voici quelques exemple :
-
$ku'\sqrt{u}$ correspond à $ku'u^n$ avec $n=\dfrac{1}{2}$ car $\sqrt{u} =u^{\frac{1}{2}}$.
-
$\dfrac{ku'}{\sqrt{u}}$ correspond à $ku'u^n$ avec $n=-\dfrac{1}{2}$ car $\dfrac{1}{\sqrt{u}}=u^{-\frac{1}{2}}$.
-
$\dfrac{ku'}{u^2}$ correspond à $ku'u^n$ avec $n=-2$ car $\dfrac{1}{u^2}=u^{-2}$.
-
$\dfrac{ku'}{u^p}$ correspond à $ku'u^n$ avec $n=-p$ car $\dfrac{1}{u^p}=u^{-p}$.
Lorsque vous avez une fraction avec une puissance négative, vous pouvez remonter la puissance en changeant le signe de l'exposant.
Repérer la forme des globlales des fonctions $f$ suivantes puis utliser le tableau précédent afin d'obtenir une primitive $F$ de $f$ sur $I$.
-
$f(t)=2t(t^2+9)^6$ sur $I=\mathbb{R}$.
-
$f(t)=5e^{3-2t}$ sur $I=\mathbb{R}$.
-
$f(t)=\dfrac{4t}{t^2+1}$ sur $I=\mathbb{R}$.
Voici les étapes à suivre en général pour déterminer une primitive (particulière) d'une fonction $f$.
-
Étape 1 : Reconnaître une forme pour $f$ et/ou une fonction usuelle pour déterminer une primitive.
-
Étape 2 : Déterminer la forme générale de la primitive en n’oubliant pas la constante $C$ en s'aidant des tableaux précédents (à connaître).
-
Étape 3 : Éventuellement, si on connaît l’image d’un réel donné et que l'on cherche une primitive particulière, on détermine cette constante $C$ en résolvant une équation.
Pour déterminer une primitive de $f$ définie sur $I=\mathbb{R}$ par $f(t)=t^2(t^3+1)^5$ :
-
$f$ est de la forme $ku'u^n$ avec $n=5$, $u(t)=t^3+1$ et donc $u'(t)=3t^2$.
Reste à trouver la constante $k$. En identifiant le facteur devant $(t^3+1)^5$ et celui devant $u^n$, on peut écrire l'équation : $ku'=t^2$.
Ainsi, en remplaçant $u'$ par son expression, : $k\times 3t^2=t^3$, soit $3k=1$, d'où $k=\dfrac{1}{3}$. -
Comme $f=\dfrac{1}{3}u'u^5$, les primitives $F$ de $f$ sont de la forme $F(t)=\dfrac{1}{3}\times\dfrac{u^{5+1}}{5+1}+C$, avec $C\in\mathbb{R}$.
Ainsi, les primitives de $f$ sur $\mathbb{R}$ sont les fonctions $F:t\mapsto\dfrac{1}{3}(t^3+1)^6+C$, où $C$ est un réel quelconque.
-
Déterminer une primitive de $f$ définie sur $I=\mathbb{R}$ par $f(t)=4t(t^2+4)^3$.
Déterminer les primitives de $f$ définie sur $I=]1;+\infty[$ par $f(t)=\dfrac{t}{t^2-1}$.
Déterminer la primitive $F$ de $f$ définie sur $I=]0;+\infty[$ par $f(t)=\dfrac{1}{t^2}e^{\frac{1}{t}}$ telle que $F(1)=0$.
Lorsque l'on recherche une primitive d'un produit et qu'on ne reconnaît pas une forme $ku'u^n$, où $k\in\mathbb{R}$, il est souvent utile de transformer ce produit en somme.
Déterminer une primitive sur $]0;+\infty[$ de la fonction $f:t\mapsto \dfrac{4t^5-3t+1}{2t^3}$.
-
Si l'on considère la forme $k\dfrac{u'}{u}$, alors il faudrait que $u(t)=2t^3$.
Comme alors $u'(t)=2\times 3t^2$, il faudrait que $ku'=4t^5-3t+1$, donc que $k=\dfrac{4t^5-3t+1}{6t^2}$. Ceci n'est pas possible car $k$ doit être une constante réelle. -
Si l'on considère la forme $k\dfrac{u'}{u^3}$, alors il faudrait que $u(t)=t$.
Comme alors $u'(t)=1$, il faudrait que $ku'=4t^5-3t+1$, donc que $k=\dfrac{1}{2}\times (4t^5-3t+1)$. Ceci n'est pas possible car $k$ doit être une constante réelle.
Comme aucune des formes du second tableau ne convient, il reste l'idée de tranformer le quotient $f(t)$ sous forme d'une somme.
$f(t)=\dfrac{4t^5-3t+1}{2t^3}=\dfrac{4t^5}{2t^3}-\dfrac{3t}{2t^3}+\dfrac{1}{2t^3}$ $=2t^2-\dfrac{3}{2t^2}+\dfrac{1}{2t^3}$.
Ainsi, les primitives $F$ de $f$ sur $]0;\infty[$ sont de la forme
$F(t)=2\times\dfrac{t^3}{3}-\dfrac{3}{2}\times\left(-\dfrac{1}{t}\right)+\dfrac{1}{2}\times\left(-\dfrac{1}{2}\times\dfrac{1}{t^2}\right)+C$,
soit $F(t)=\dfrac{2t^3}{3}+\dfrac{3}{2t}-\dfrac{1}{4t^2}+C$, avec $C\in\mathbb{R}$.
Déterminer une primitive de $f$ définie sur $]0,+\infty[$ par $f(t)=\dfrac{4t^4-2t^3+t^2-t+4}{t^2}$.
Lorsque l’on trouvé une primitive d’une fonction et que l’on doute de son résultat, il est prudent de procéder à une vérification en dérivant la primitive obtenue.
Galilée fait tomber depuis une tour une pierre de masse 1 kg au temps $t=0$ avec une vitesse initiale de $3 m.s^{-1}$.
On admet que l’accélération subie par la pierre est donnée au temps $t$ par $a(t)=10$.
-
Quelle est la vitesse $v(t)$ de la pierre au temps $t$ ?
$v'(t)=a(t)$ : $v$ est une primitive de $a$ sur $\mathbb{R}$.
-
À l’instant $t$ de quelle distance $d(t)$ a déjà chu la pierre ?
$d'(t)=v(t)$.
-
À quelle instant la pierre touchera-t-elle le sol sachant que la tour a une hauteur de 54 mètres ?
Décomposition en éléments simples
Soit $f$ la fonction définie sur $]1;+\infty[$ par $f(t)=\dfrac{2t^2-3t+4}{(t-1)^2}$.
-
Est-ce que les formes vues dans le cours permettent de trouver une primitive à $f$ ?
-
Sous quelle autre forme générale serait-il intéressant d'écrire l'expression $f(t)$ ?
L'instruction partfrac de Xcas permet d'obtenir la décomposition d'une fonction rationnelle (=quotient de
deux polynômes) sous la forme d'une somme d'éléments plus simples.
On considère comme à l'exercice précédent la fonction $f$ définie sur $]1;+\infty[$ par $f(t)=\dfrac{2t^2-3t+4}{(t-1)^2}$.
-
Utiliser Xcas pour déterminer les réels $a$, $b$ et $c$ tels que, pour tout réel $t>1$, $f(t)=a+\dfrac{b}{t-1} +\dfrac{c}{(t-1)^2}$.
-
En déduire la primitive $F$ de $f$ sur $]1;+\infty[$ telle que $F(2)=6$.
Primitive à l'aide du logiciel Xcas
-
Voici ci-contre deux affichages donnés par le logiciel Xcas :

Que permet de calculer l'instructionint? -
Comment vérifier, par calcul à la main, les primitives proposées par Xcas ?
Intégration
Interprétation graphique
a. Cas où $f$ est positive
-
L'unité d’aire ( u.a.) est l’aire du rectangle construit à partir des points $O$, $I$ et $J$.
-
Soit $f$ une fonction continue et positive sur $[a;b]$ et $\mathcal{C}_f$ sa courbe représentative dans $(O ; \overrightarrow{i}, \overrightarrow{j})$.
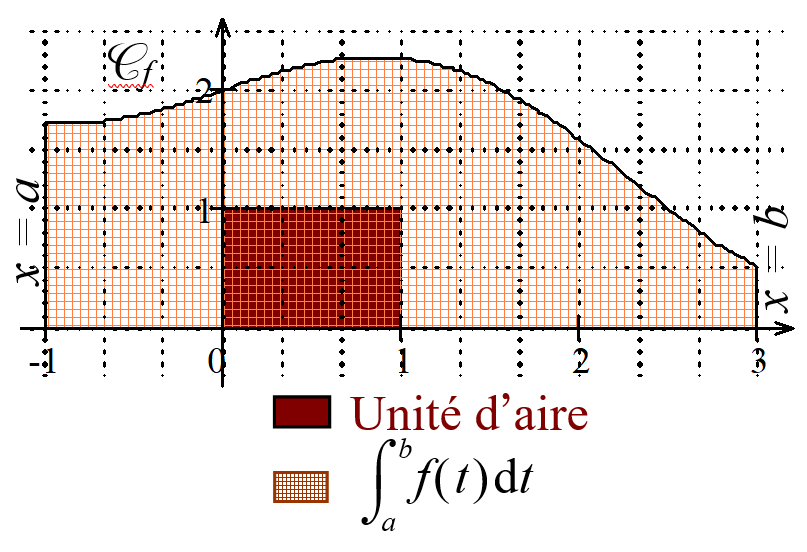
On appelle intégrale de la fonction $f$ sur l’intervalle $[a;b]$ le réel représentant l’aire, en unité d’aire,
du domaine situé sous $\mathcal{C}_f$, c’est-à-dire de la portion du plan délimité par $\mathcal{C}_f$, l’axe des abscisses
et les droites verticales d’équation $x=a$ et $x=b$.
Ce réel est noté $\displaystyle \int^b_a{f(t)dt}$.
-
Si $OI=2cm$ et $OJ=3cm$ alors $1u.a.=6cm^2$.
-
Les réels $a$ et $b$ sont appelés les bornes de l’intégrale.
-
La variable $t$ de $\displaystyle \int^b_a{f(t)dt}$ est dite variable muette et peut être remplacée par n’importe qu’elle lettre : $\displaystyle \int^b_a{f(t)dt}=\int^b_a{f(x)dx}=\int^b_a{f(y)dy}=\int^b_a{f(\theta)d\theta}=...$
Calcul de $\displaystyle \int^3_{-1}{7dt}$.
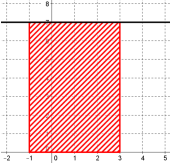
$\displaystyle \int^3_{-1}{7dt}$ correspond à l'aire d'un rectangle de base 4 et de hauteur 7. Ainsi, $\displaystyle \int^3_{-1}{7dt}=base\times hauteur=7\times (3-(-1))=7\times 4=28$.
-
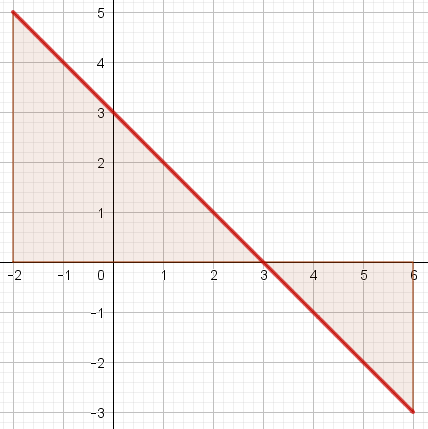
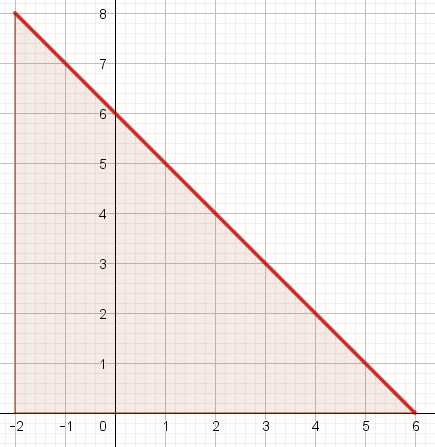
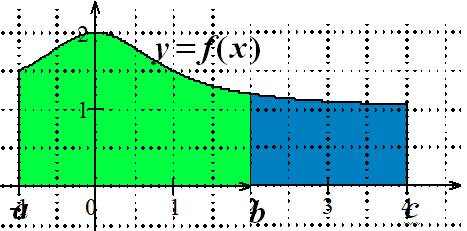
Parmi les représentations graphiques suivantes, laquelle représente l'intégrale $\displaystyle \int^3_{-1}{(6-2t)dt}$ ?
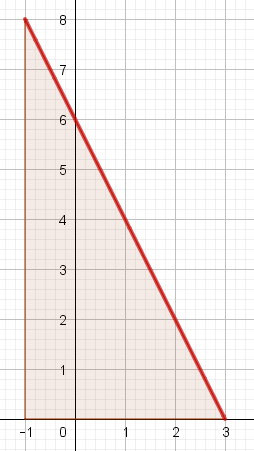
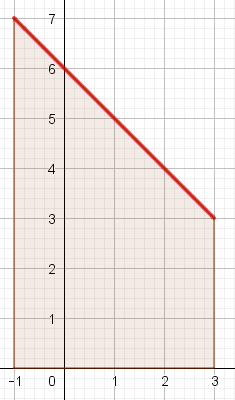
-
En déduire la valeur de l'intégrale $\displaystyle \int^3_{-1}{(6-2t)dt}$.
b. Cas où $f$ est négative
Soit $f$ une fonction continue et négative sur $[a;b]$.
L’intégrale de $f$ sur [a;b] est définie par $\displaystyle \int^b_a{f(t)dt}=-\int^b_a{|f(t)|dt}$.
Cette intégrale un nombre négatif : on parle d'aire algébrique.
Détermination graphique de $\displaystyle \int^5_1{-2dt}$.
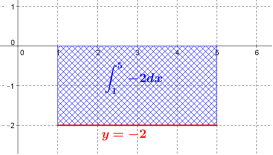
Tracer la fonction $t\mapsto -2$ sur $[1;5]$.
La fonction est négative sur $[1;5]$ donc l'aire est négative.
L'intégrale cherchée est l'aire négative d'un rectangle $\displaystyle \int^5_1{-2dt}=-2\times(5-1)=-8$.
c. Cas général
Soit $f$ une fonction continue sur $[a;b]$ et $\mathcal{C}_f$ sa courbe représentative.
L'intégrale de $f$ sur $[a;b]$ est la somme des aires algébriques des domaines définis à partir des intervalles sur lesquels
$f(t)$ garde un signe constant.
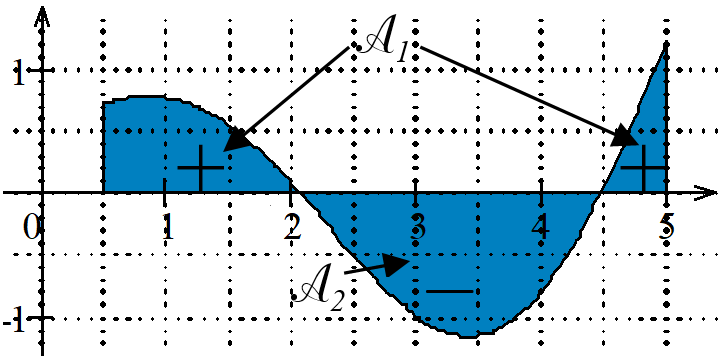
L’intégrale de $f$ sur $[a;b]$ est définie par $\displaystyle \int^b_a{f(t)dt}=\mathcal{A}_1-\mathcal{A}_2$, où :
-
$\mathcal{A}_1$ est l’aire de la partie du plan délimitée par la courbe $\mathcal{C}_f$, l’axe des abscisses et les droites verticales d’équation $x=a$ et $x=b$, et située au-dessus de l’axe des abscisses,
-
$\mathcal{A}_2$ est l’aire de la partie du plan délimitée par la courbe $\mathcal{C}_f$, l’axe des abscisses et les droites verticales d’équation $x=a$ et $x=b$, et située en-dessous de l’axe des abscisses.
d. Extension de la définition à $a$ et $b$ quelconque
Soit $f$ une fonction continue sur $I$. Soient $a$ et $b$ dans $I$.
Si $a\gt b$, alors on définit $\displaystyle \int^b_a{f(t)dt}$ par $\displaystyle \int^b_a{f(t)dt}=-\int^a_b{f(t)dt}$.
Définition à l'aide d'une primitive
Soit $f$ une fonction définie sur un intervale $I$, $a$ et $b$ deux éléments de $I$ et $F$ une primitive de $f$ sur $I$.
On appelle intégrale de $a$ à $b$ de $f$ sur $I$ le nombre réel : $F(b)-F(a)$.
On le note : $\displaystyle \int^b_a{f(t)dt}=[F(t)]_a^b=F(b)-F(a)$.
Calculer les deux intégrales suivantes (quitte à s'aider de Xcas pour trouver une primitive de la fonction intégrée).
Repérer la fonction comprise entre le symbole $\displaystyle \int^b_a$ et $dt$, puis trouver une primitive $F$ de cette fonction, enfin calculer $F(b)-F(a)$.
-
$\displaystyle \int^3_0{(5t^2-t+4)dt}$.
-
$\displaystyle \int^e_1{\dfrac{1}{t}dt}$.
Calcul d'intégrale sur Xcas
Pour obtenir la valeur de l'intégrale $\displaystyle \int^b_a{f(t)dt}$, il suffit de saisir sur Xcas :
int(f(t),t,a,b), c'est-à-dire de prendre la même instruction que pour le calcul de primitive mais
en précisant la valeur des deux bornes.
Pour obtenir la valeur de $\displaystyle \int^8_1{\dfrac{4}{t}dt}$, on saisit :
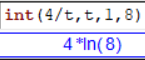
Ainsi, $\displaystyle \int^8_1{\dfrac{4}{t}dt}=4\ln(8)$.
Calculer les primitives suivantes à l'aide de Xcas :
-
$\displaystyle \int^2_1{\dfrac{t}{t^2-9}dt}$.
-
$\displaystyle \int^e_2{\dfrac{1}{t}\ln(t)dt}$.
-
$\displaystyle \int^{\sqrt{3}}_1{\dfrac{4}{t^2+1}dt}$.
Quelques propriétés de l'intégrale
Relation de Chasles
$f$ et $g$ désignent deux fonctions continues sur un intervalle $I$.
La relation de Chasles :
Pour tous les réels $a$, $b$ et $c$ dans $I$ : $\displaystyle \int^c_a{f(t)dt}$ $=\displaystyle \int^b_a{f(t)dt}+\int^c_b{f(t)dt}$
Voici une conséquence :
Si $f$ est une fonction impaire sur $[-a;a]$ avec $a\lt 0$, alors $\displaystyle \int^a_{-a}{f(t)dt}=0$
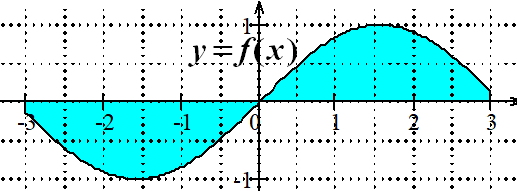
Calculer sans utiliser Xcas $\displaystyle \int^{\pi}_{-\pi}{\sin(t)dt}$.
Linéarité de l'intégrale
Pour tous les réels $\alpha$ et $\beta$ : $\displaystyle \int^b_a{(\alpha f(t)+\beta g(t))dt}=\alpha \int^b_a{f(t)dt} + \beta \int^b_a{g(t)dt}$
Calculer $\displaystyle \int^1_0{e^t (\sin(t))^2 dt}+\int^1_0{e^t (\cos(t))^2 dt}$.
Vous pouvez admettre que pour tout réel $t$ : $\sin(t))^2 + (\cos(t))^2 =1$.
Conservation de l'ordre
Si pour réel $t$ de $[a;b]$ $f(t)\ge g(t)$, alors $\displaystyle \color{red}{\int^b_a{\color{black}{f(t)}\color{red}{dt}}}\color{black}{\ge} \color{red}{\int^b_a{\color{black}{g(t)}\color{red}{dt}}}$.
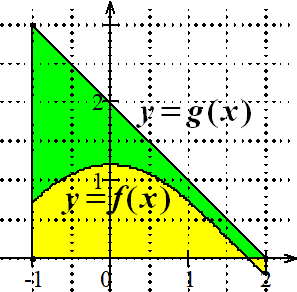
Un cas particulier très utile :
Positivité de l'intégrale :
Si $f$ est positive sur $[a;b]$ alors $\displaystyle \int^b_a{f(t)dt} \ge 0$.
On retrouve dans cette dernière propriété qu'une aire est positive lorsque la courbe représentant la fonction est au-dessus de l'axe des abscisses.
Voici la représentation graphique de la fonction $t\mapsto \dfrac{2}{1+t^2}$ sur l'intervalle $[0;3]$.
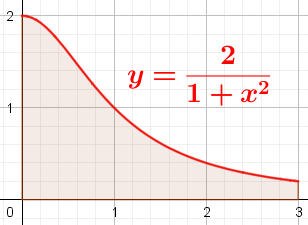
Encadrer $f$ sur $[0;3]$ pour justifier que $\displaystyle 0\le \int^3_0{\dfrac{2}{1+t^2}dt} \le 6$.
Voici la courbe représentant la fonction exponentielle ainsi que sa tangente au point d'abscisse 0 :
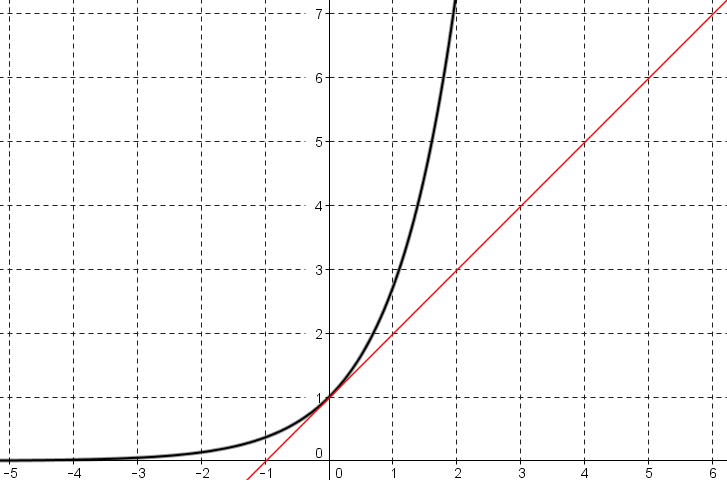
-
Déterminer l'équation de la tangente tracée.
-
Utiliser la courbe précédente pour comparer les deux fonctions $f:t\mapsto e^t$ et $g:t\mapsto t+1$.
-
Utiliser la conservation de l'ordre à partir de l'inégalité précédente pour obtenir une comparaison d'intégrales définies sur l'intervalle $[0;x]$.
-
En déduire que pour tout réel $x\ge 0$ : $e^x\ge \dfrac{x^2}{2}+x+1$.
Valeur moyenne
Soit $f$ une fonction continue sur $[a;b]$.
La valeur moyenne de $f$ sur $[a;b]$ est le réel $\displaystyle \dfrac{1}{b-a} \int^b_a{f(t)dt}$.
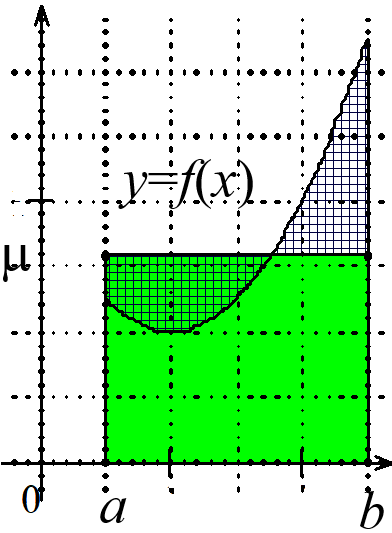
Voici une interprétation graphique de cette valeur moyenne :
La valeur moyenne $\mu$ est le réel tel que l’aire du domaine associé à la fonction $f$ soit égale à l’aire du rectangle
de base de longueur $b-a$ et de hauteur $\mu$.
Vous venez d'acheter un terrain rectangulaire afin d'y construire une maison. Le seul problème de ce terrain est qu'il n'est pas plat. Vous décidez donc de le niveler.
Le profil de votre terrain est donné par la fonction $h$ définie sur $[0;400]$ par $h(x)=\dfrac{x^2}{1600}-\dfrac{x}{4}+125$ ;
$h(x)$ correspond à la hauteur au-dessus du niveau de la mer du point se trouvant à $x$ mètres du bord gauche du terrain.
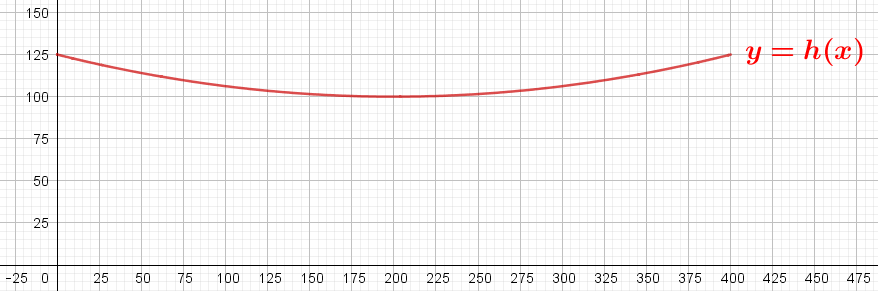
-
Déterminer graphiquement ci-dessous une valeur approchée de la hauteur du terrain une fois nivelé pour que les remblais équilibrent exactement les déblais ? (On suppose ici qu'il y a une conservation du volume)
-
Calculer la valeur moyenne de $h$ sur $[0;400]$.
Qu'en déduire quant au terrain nivelé ?
La capacité pulmonaire en litres, d'un être humain suivant son âge $t$, compris entre 10 et 90 ans, peut être
modélisé par la fonction $c$ définie sur $[10;90]$ par $c(t)=\dfrac{110(\ln(t)-2)}{t}$.
Déterminer la valeur moyenne de la capacité pulmonaire d'un être humain entre 20 et 60 ans. (Donner la valeur
exacte puis une valeur approchée au décilitre près)
Valeur efficace
En physique, vous aurez besoin de la notion de valeur efficace.
Soit $f$ une fonction continue sur l'intervalle $[a;b]$.
La valeur efficace de la fonction $f$ sur l'intervalle $[a;b]$ est le réel $f_{eff}$ défini
par $f_{eff}=\displaystyle \sqrt{\dfrac{1}{b-a}\times\int_a^b{f^2(t)dt}}$.
On considère une tension $U$ définie sur l'intervalle de temps $[0;2]$ par $U(t)=6\sin\left(5\pi t+\dfrac{\pi}{2}\right)$. Déterminer la valeur efficace de cette tension sur $[0;2]$.
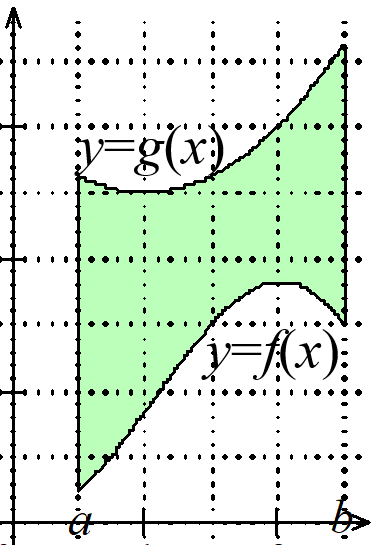
Aire entre deux courbes
Soient $f$ et $g$ deux fonctions continues sur $[a;b]$ dont les représentations graphiques sont
$\mathcal{C}_f$ et $\mathcal{C}_g$.
Supposons que $f\le g$ sur $[a;b]$.
L'aire située entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ et les droites verticales d'équation $x=a$ et $x=b$ est :
$\displaystyle \int^{b}_{a}{g(t)dt}-\int^{b}_{a}{f(t)dt}$, soit par linéarité aussi
$\displaystyle \int^{b}_{a}{\left(g(t)-f(t)\right)dt}$.
Ci-contre sont représentées les fonctions exponentielles et logarithme népérien.
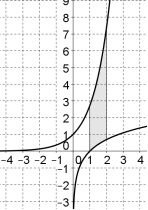
Déterminer l'aire de la zone grisée.
Lien avec la cinématique
-
Pour un mobile se déplaçant sur une droite, ou sur toute ligne « continue » à la vitesse instantanée $v(t)$ ($t$ est le temps), toujours positive ou nulle, la distance parcourue entre les instants $t_1$ et $t_2$ s’exprime par $\displaystyle d=\int^{t_2}_{t_1}{v(t)dt}$.
-
La vitesse moyenne d’un mobile est la valeur moyenne de la vitesse.
En effet, avec la notation donnée, on a :
$\text{vitesse moyenne} $ $=\dfrac{\text{distance parcourue}}{\text{durée écoulée}}$ $\displaystyle =\dfrac{1}{t_2-t_1}\int^{t_2}_{t_1}{v(t)dt}$ $=\text{valeur moyenne de la vitesse}$.
Intégration par parties
Cette partie au programme est exclue de tout CCF. Elle s'adresse aux étudiants qui poursuivront des études nécessitant des mathématiques après le BTS SNIR.
Nous avons déjà vu que lorsque l'on veut calculer à la main une intégrale, il suffit de trouver une primitive à la fonction
sur l'intervalle considéré.
Nous avons aussi vu que lorsque l'on n'arrive pas à trouver une primitive avec les formes usuelles, une idée est de chercher
à écrire la forme sous forme d'éléments plus simples à intégrer (utilisation de partfrac sur Xcas).
Dans cette partie, nous allons voir que parfois il est posible d'écrire un produit à l'aide d'un autre produit, produit
qui lui pourra dans certais cas être plus facilement intégrable.
Théorème de l'intégration par parties
Soient $u$ et $v$ deux fonctions continues sur $I$ telles que $u'$ et $v'$ soient continues sur un intervalle $I$.
Alors, pour tous réels $a$ et $b$ de $I$, $\displaystyle \int^b_a{u(t)v'(t)dt}=[u(t)v(t)]^b_a-\int^b_a{u'(t)v(t)dt}$.
Pour calculer l'intégrale $\displaystyle \int^{\frac{\pi}{2}}_0{x\cos xdx}$, il suffit d'appliquer la méthode suivante (en repérant qu'une primitive de $x\mapsto \cos x$ est $x\mapsto -\sin x$) :
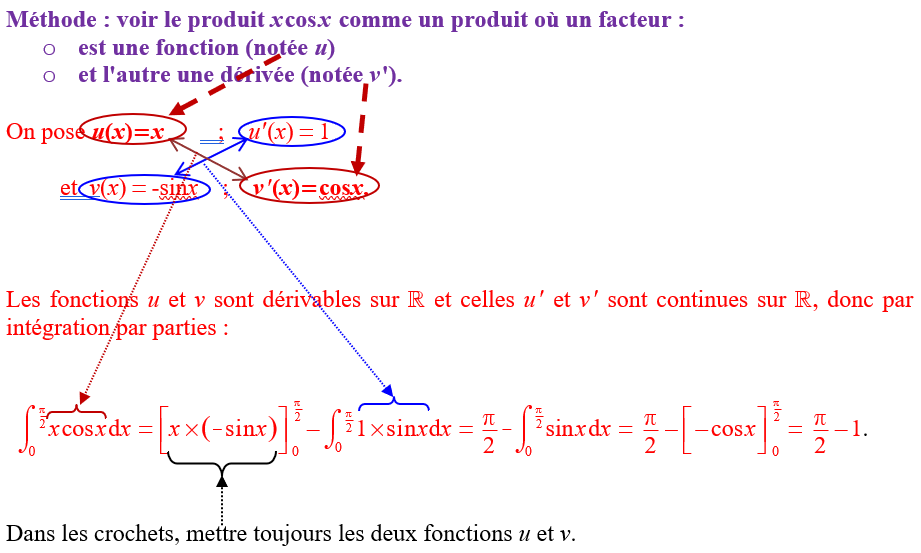
Dans le schéma de l'exemple liant $u$, $u'$, $v$ et $v'$, une intégrale correspond à une diagonale du
produit en croix issu des 4 expressions.
L'intégrale qui apparaîtra en appliquant l'intégration par parties, correspond à l'autre diagonale du produit en croix.
Pour savoir quel facteur considérer comme fonction à dériver et quel autre comme dérivée à intégrer, vous pouvez admettre et utiliser la propriété suivante :
Soit $P$ une fonction polynôme.
-
Pour calculer $\displaystyle \int^b_a{P(t)e^t dt}$, $\displaystyle \int^b_a{P(t)\cos(t) dt}$ ou $\displaystyle \int^b_a{P(t)\sin(t) dt}$, on pose $u(t)=P(t)$ et $v'(t)=e^t$, $\cos(t)$ ou $\sin(t)$.
-
Pour calculer $\displaystyle \int^b_a{P(t)\ln(t) dt}$, on pose $u(t)=\ln(t)$ et $v'(t)=P(t)$.
Calculer à la main par intégration par parties l'intégrale suivante : $\displaystyle \int^e_1{x^2\ln(x)dx}$.
Exercices
Justifier une primitive
Justifier par un calcul (à la main ou sur Xcas) que $F:t\mapsto t e^{3t}$ est une primitive de $f:t\mapsto (3t+1)e^{3t}$ sur $\mathbb{R}$.
Calculer à la main une primitive
-
En s'aidant du premier tableau du cours, déterminer une primitive de chacune des fonctions suivantes sur $]0;+\infty[$ :
-
$f_1(t)=6t-5$.
-
$f_2(t)=t^3$
-
$f_3(t)=\dfrac{1}{t^4}$
-
$f_4(t)=-\dfrac{1}{t}$
-
$f_5(t)=3e^t$
-
-
En utilisant les primitives précédemment trouvées, déterminer une primitive de la fonction $g$ définie sur $]0;+\infty[$ par $g(t)=6t-5+t^3+ \dfrac{1}{t^4} -\dfrac{1}{t}+3e^t$.
Déterminer une primitive des fonctions suivantes sur l'intervalle $I$ proposé :
-
$f:t\mapsto 4t^2-5t+2-\dfrac{3}{t^2}$ sur $I=]0;+\infty[$.
-
$f:t\mapsto \dfrac{2}{t}-\dfrac{3}{t^4}$ sur $I=]0;+\infty[$.
-
$f:t\mapsto \dfrac{e^t}{2}-\dfrac{3}{\sqrt{t}}$ sur $I=]0;+\infty[$.
Déterminer une primitive des fonctions suivantes sur l'intervalle $I$ proposé :
-
$f:t\mapsto 2t^2+2t-4$ sur $I=\mathbb{R}$.
-
$f:t\mapsto \dfrac{3}{t^2}$ sur $I=]0;+\infty[$.
-
$f:t\mapsto e^t+\dfrac{2}{\sqrt{t}}-2\cos(t)+t$ sur $I=]0;+\infty[$.
-
$f:t\mapsto (2t+1)(t^2+t-1)^5$ sur $I=\mathbb{R}$.
-
$f:t\mapsto \dfrac{7}{(2t+1)^4}$ sur $I=]0;+\infty[$.
-
$f:t\mapsto \dfrac{-15t^2-10}{(t^3+2t)^2 }$ sur $I=]0;+\infty[$.
-
$f:t\mapsto 4-\dfrac{t}{t^2+16}$ sur $I=\mathbb{R}$.
-
$f:t\mapsto \dfrac{\ln(t)}{t}$ sur $I=]0;+\infty[$.
Déterminer la primitive $F$ de $f$, fonction définie sur $\mathbb{R}$ par $f(t)=te^{-t^2}$, telle que $F(0)=2$.
Déterminer la primitive $F$ de $f$, fonction définie sur $\mathbb{R}$ par $f(t)=\dfrac{e^{-t}}{1+e^{-t}}$, telle que $F(0)=0$.
On se propose de déterminer le moment fléchissant en un point M de la poutre AB de longueur 6 mètres,
$x$ est exprimé en mètres.
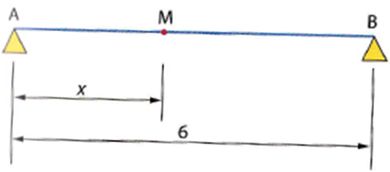
Toutes les fonctions de cet exercice sont définies sur l'intervalle $I=[0;6]$.
Soit $f$ la fonction définie sur $I$ par $f(x)=-600x$.
-
Déterminer la primitive $F$ de $f$ pour laquelle $F(0)=3600$.
-
Déterminer la primitive $G$ de $F$ pour laquelle $G(0)=0$.
Le nombre G(x) représente le moment fléchissant de la poutre au point M.
Les poutres sollicitées en flexion sont importantes dans la résistance des matériaux. Dans le cas de la flexion, les efforts intérieurs dans n'importe quelle section droite se réduisent à un effort tranchant et à un moment fléchissant.
Décomposition en éléments simples
Le but est de calculer la primitive de $f:t\mapsto \dfrac{5t^2+21t+22}{(t-1)(t+3)^2}$ sur $]1;+\infty[$.
-
Déterminer les réels $a$, $b$ et $c$ tels que $f(t)= \dfrac{a}{t-1} + \dfrac{b}{t+3} +\dfrac{c}{(t+3)^2}$.
-
En déduire la primitive $F$ de $f$ qui s'annule en 2.
Utiliser Xcas pour déterminer les réels $A$ et $B$ tels que, pour tout réel $t$ différent de $-2$, on a : $\dfrac{4-3t}{(t+2)^2}=\dfrac{A}{t+2}+\dfrac{B}{(t+2)^2}$.
Interprétation graphique
-
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=(x+2)e^{-x}$.
Ci-dessous est tracée la courbe $\mathcal{C}_f$.
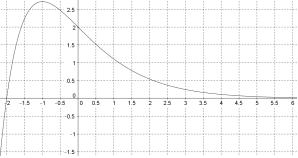
Reproduire grossièrment la courbe sur une feuille et hachurer sur le graphique le domaine dont l’aire est donnée par $\displaystyle \int_0^2{f(t)dt}$. -
La courbe ci-dessous représente la fonction $f$ définie sur $[0.5;7]$ par $f(t)=4+(0.5t-3)\ln(t)$.
Déterminer la valeur exacte de l'aire hachurée sur le graphique :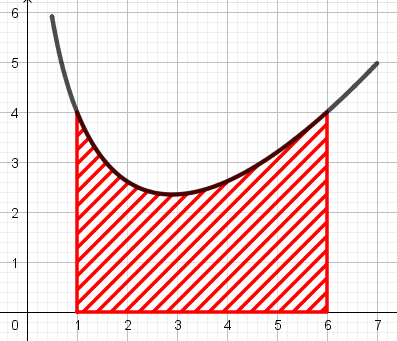
Problèmes concrets
Une denrée alimentaire est placée dans un tunnel de congélation maintenu à -30°C.
Au tunnel de congélation, on associe un compresseur bicylindre. La compression est considérée comme isotherme
à température constante.
Le travail $W$ mis en jeu dans un des cylindres pour une compression est donné par la relation :
$\displaystyle W=\int_{0.041}^{0.204}\dfrac{323}{v} dv$.
-
Déterminer, en joules, le travail $W$.
-
Arrondir à l'unité près le résultat.
La proportion d’individus qui possèdent un certain type d’équipement dans une population est modélisée par la fonction
$p$ définie sur $[0;+\infty[$ par $p(t)=\dfrac{1}{1+e^{-0.2t}}$.
Le réel $t$ représente le temps écoulé, en année, depuis le 1er janvier 2020. Le nombre $p(t)$ modélise la
proportion d’individus équipés après $t$ années.
Ainsi, pour ce modèle, $p(0)$ est la proportion d’individus équipés au 1er janvier 2020 et $p(3,5)$ est
la proportion d’individus équipés au milieu de l’année 2023.
Déterminer la valeur exacte de la proportion moyenne d’individus équipés entre 2022 et 2030 puis son arrondi au millième.
La figure ci-dessous représente une section de tuyère. Cette tuyère est obtenue par rotation autour
de l'axe des abscisses de la partie du plan coloriée.
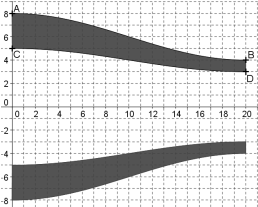
-
L'arc $\overset{\huge{\frown}}{AB}$ représente la fonction $f$ définie par $f(x)=2\cos\left(\dfrac{\pi x}{20}\right)+6$ sur $[0;20]$.
-
L'arc $\overset{\huge{\frown}}{CD}$ représente la fonction $g$ définie par $g(x)=\cos\left(\dfrac{\pi x}{20}\right)+4$ sur $[0;20]$.
-
Écrire l'aire de la section $ABCD$ de la tuyère à l'aide d'une intégrale.
-
Calculer l'aire de la section $ABCD$ de la tuyère.
-
On admet que le volume de la tuyère est donnée par : $V=\pi\int_0^{20}{\left[(f(x))^2-(g(x))^2\right]dx}$.
Déterminer le volume de la tuyère.
Dans une entreprise, lors d’une intervention sur la sécurité routière, on s’intéresse au taux d’alcool dans le sang. Dans cet exercice, ce taux est exprimé en $g.L^{-1}$.
Partie A : lectures graphiques
Une personne a ingéré une certaine quantité d’alcool.
On s’intéresse à l’évolution du taux d’alcool dans le sang de cette personne, en fonction du temps $t$, en heures.
Compte tenu du délai d’absorption par l’organisme, le taux d’alcool dans le sang de cette personne est donné par la
fonction $f$ définie sur $[0,025;+\infty[$ par $f(t)=(2t-0.05)e^{-t}$.
La représentation graphique est donnée ci-dessous :
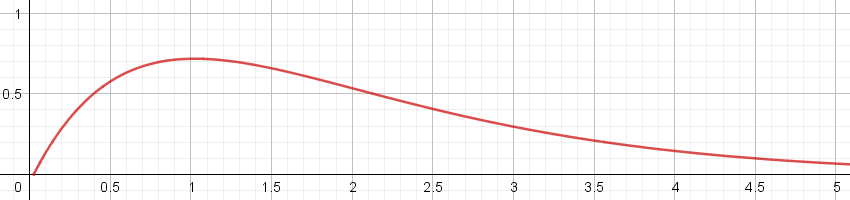
-
Déterminer graphiquement pendant combien de temps le taux d’alcool dans le sang de cette personne reste supérieur à $0.5 g.L^{-1}$,.
-
Déterminer graphiquement à quel instant le taux est maximum et donner ce maximum.
Partie B : utilisation de Xcas
-
Déterminer la valeur exacte du maximum de la fonction $f$ et l'instant où il est atteint.
-
Déterminer le taux d'alcool moyen, en $g.L^{-1}$, entre les instants $t=2$ et $t=4$.
Un laboratoire pharmaceutique veut produire un médicament pour les nourrissons sous forme d'un suppositoire.
La courbe d’équation $y=f(x)$ avec $f(x)=\dfrac{\ln x}{x}$ avec $x\in \left[1;e^2\right]$ dans un repère orthonormal
$(O ; \overrightarrow{i}, \overrightarrow{j})$, tournant autour de l’axe $(O ; \overrightarrow{i})$,
engendre le solide de révolution correspond au suppositoire. On note $V$ son volume.
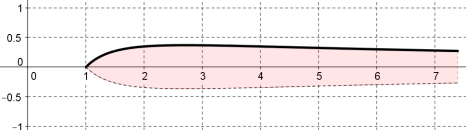
-
On admet que $V=\pi\int_1^{e^2}{(f(x))^2dx}$. Déterminer $V$.
-
Quelle est la largeur maximale du diamètre du suppositoire ?
On estime que les futures découvertes de pétrole dans le monde peuvent être modélisées, à partir de $2015$, par la fonction $f$ définie sur $[15;+\infty[$ par $f(t)=17280 exp(-0.024t)$, où $f(t)$ représente, en millions de barils, l'estimation de la quantité de pétrole qui sera découverte au cours de l'année $2000+t$.
-
Quelle quantité de pétrole fut découverte en $2015$ ?
-
Quelle quantité de pétrole sera découverte à très long terme ? Justifier.
-
Dresser le tableau de variation de $f$ sur $[15;+\infty[$. Interpréter concrètement ces variations.
-
Quelle quantité moyenne de pétrole sera découverte sur la décennie $2020-2030$ ?
-
Déterminer la quantité de pétrole qui sera découverte entre $2015$ et $2100$ selon ce modèle.
Les verres photochromiques s'assombrissent ou s'éclaircissent en fonction de la luminosité.
Pour un verre minéral photochromique, le coefficient de transmission, exprimé en pourcentage, en fonction de la longueur
d'onde $x$, en nm, est donné par : $f(x)=90- \dfrac{89}{1+e^{\frac{x-416}{5}}}$.
-
Est-il vrai que le coefficient de transmission augmente lorsque la longueur d'onde est plus grande ?
-
On admet que la quantité d'énergie $I$ absorbée par le verre durant la transition sombre/clair est donnée par l'intégrale : $\int_{380}^{550}{f(x)dx}$.
Donner la valeur exacte puis une approchée à $10^{-2}$ de $I$.
Entre deux poteaux électriques distants de 200 mètres, un fil électrique est suspendu. On admet que dans un repère centré sur le milieu entre ces deux poteaux, la hauteur en mètre d'une ligne électrique peut être modélisée par la fonction $h$ définie sur $[-100;100]$ par $h(x)=150\left( e^{\frac{x}{300}}+e^{-\frac{x}{300}} \right)$.
-
-
Déterminer une primitive de $f:x\mapsto e^{\frac{x}{300}}+e^{-\frac{x}{300}}$ sur $[-100;100]$.
-
Déterminer la hauteur moyenne de la ligne électrique.
-
-
-
Prouver que la hauteur minimale est atteinte en $x=0$.
-
La flèche de la ligne est l'écart de hauteur entre le point le plus haut de la courbe et celui le plus bas.
Calculer la valeur de la flèche.
-
-
On admet que la longueur de l'arc de courbe d'équation $y=f(x)$ compris entre les points d'abscisses $a$ et $b$ est donnée par $\displaystyle \int_a^b{\sqrt{1+(f'(x))^2} dx}$.
En déduire la valeur exacte puis approchée, au centimètre près, de la longueur du fil électrique suspendu.
A la suite d'un accident de la circulation, un camion-citerne déverse une partie de son contenu sur la chaussée
d'une autoroute. La réglementation en vigueur impose l'isolation, par fermeture des vannes, du bassin de
décantation proche de l'accident de façon à ce que la concentration en matière polluante du bassin ne
dépasse par 15 $\mu g.L^{-1}$.
Cette concentration est de 1.3 $\mu g.L^{-1}$ au moment où les matières polluantes provenant du camion-citerne
commencent à se déverser dans le bassin. On mesure en minutes le temps t écoulé à partir de l'instant
où les matières polluantes provenant du camion-citerne commencent à se déverser dans le bassin de décantation.
On admet que, tant que le bassin n'est pas isolé par fermeture des vannes, la concentration à l'instant $t$ en matières polluantes dans le bassin, exprimé en $\mu g.L^{-1}$, peut être modéliser par $f(t)$ où $f$ est la fonction définie sur l'intervalle $[0;+\infty[$ par $f(t)=25-23.7 e^{-0.03t}$.
-
Si le bassin n'était pas équipé d'un dispositif d'isolation par fermeture des vannes, quelle serait la valeur autour de laquelle se stabiliserait la concentration en matières polluantes ? Justifier.
-
Visualiser (sur calculatrice ou sur Geogebra) la courbe représentant la fonction $f$ et déterminer graphiquement une valeur approchée à la minute près de l'instant $t_0$ au bout duquel la concentration en matières polluantes dans le bassin atteindrait 15 $\mu g.L^{-1}$ si le bassin n'était pas isolé par fermeture de vannes.
-
La concentration en matières polluantes dans le bassin est relevée par un capteur dont les mesures sont légèrement instables. Pour prendre en compte cette instabilité, on met en place un dispositif associant à la fermeture des vannes à l'instant $t$ ($t\ge 2$) la valeur moyenne de la concentration en matières polluantes mesurée par le capteur entre les instants $t-2$ et $t$.
La fermeture des vannes est déclenchée lorsque cette valeur moyenne atteint 14 $\mu g.L^{-1}$.-
Écrire la valeur moyenne $V(t)$ entre les instants $t-2$ et $t$ à l'aide d'une intégrale.
-
Donner l'expression de la valeur exacte de $V(t)$.
-
Résoudre à la main, puis avec Xcas, l'équation $25-24.4 e^{-0.03t}=14$.
On note $T$ la solution de cette équation. -
Que représente $T$ dans le contexte de cet exercice ?
-
Un TGV roulant à 360 km/h freine brusquement.
-
Exprimer sa vitesse en $m.s^{-1}$ juste avant le freinage.
-
On désigne par $a$ la fonction qui donne la décélération (en $m.s^{-2}$) en fonction du temps $t$ (en $s$). Elle est définie par $a(t)=-0.5t$.
On admet que la fonction qui donne la vitesse (en $m.s^{-1}$) en fonction du temps, est une primitive de $a$.
Déterminer la vitesse de $v(t)$ en fonction de $t$. (Pensez à utiliser la vitesse initiale avant freinage). -
On désigne par $d$ la fonction distance de freinage du TGV (en $m$) en fonction du temps, c'est à dire $d(t)$ est la distance parcourue par le TGV à l'instant $t$ depuis le début du freinage.
On admet que $d$ est la primitive de $v$ qui vérifie $d(0)=0$.
Déterminer l'expression de $d(t)$. -
Quelle est la distance de freinage nécessaire à l'arrêt du TGV ?
Une nouvelle maladie contagieuse se répend dans un territoire à partir d'un 1er février.
On note $t$ le temps écoulé en mois depuis ce 1er février.
On suppose que la proportion de personne infectée par cette maladie est donnée par la fonction $p$
définie sur $[0;+\infty[$ par $p(t)=\dfrac{1-(-30 t^2+t+1)e^{-t}}{100}$.
-
Déterminer la proportion de la population atteinte par la maladie le 1er mars.
-
Déterminer quand aura lieu le pic épidémique de cette nouvelle maladie. (au jour près)
-
Déterminer la proportion de la population qui sera infectée par cette maladie à très long terme.
Cette maladie va t'elle d'elle-même disparaître ? -
Déterminer la proportion moyenne de personnes infectées entre le 1er mars et le 1er juillet.
-
Les services d'urgence à l'hôpital peuvent tenir si la proportion de personnes infectées ne dépassent pas 0.15 pendant plus de 1 mois et demi. Les services d'urgence vont-ils tenir ?
Demander le programme !
-
La notion de primitive d'une fonction sur un intervalle.
-
Pour une fonction donnée, il y a une infinité de primitives : il suffit de rajouter (ou de modifier) une constante réelle $C$.
-
L'aire du domaine situé sous $\mathcal{C}_f$ sur l'intervalle est notée $\displaystyle \int_a^b{f(t)dt}$ : c'est l'intégrale de $f$ entre $a$ et $b$.
-
L’aire située entre les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ et les droites d’équation $x=a$ et $x=b$ est : $\displaystyle \int_a^b{g(t)dt}-\int_a^b{f(t)dt} = \int_a^b{(g(t)-f(t))dt}$.
-
La formule de la valeur moyenne d'une fonction $f$ sur un intervalle $[a;b]$ : $\displaystyle \dfrac{1}{b-a}\int_a^b{f(t)dt}$.
-
Savoir démontrer qu'une fonction est une primitive d'une autre en dérivant.
-
Savoir calculer à la main une primitive d'une fonction simple sur un intervalle.
-
Savoir calculer sur Xcas une primitive d'une fonction sur un intervalle.
-
Savoir décomposer sur Xcas une expression en somme d'éléments "simples".
-
Savoir calculer à la main une intégrale simple.
-
Savoir calculer sur Xcas une intégrale.
-
Savoir calculer à la main ou sur Xcas l'aire située entre deux courbes.
-
Savoir calculer à la main ou sur Xcas une valeur moyenne d'une fonction.

Les différents
auteurs mettent l'ensemble du site à disposition selon les termes de la licence Creative
Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0
International